
Дискретная математика. Методичка. Кацаран
.pdf
Действительно, пусть произвольное множество C Б(A B) , т. е. C A B . Обозначим через A1 = C ∩ A , B1 = C ∩ B . Тогда A1 A , B1 B и C = A1 B1 , где A1 Б(A) , B1 Б(B) . Докажем обратное включение. Если A1 Б(A) , B1 Б(B) , то A1 A , B1 B . Тогда
A1 B1 A B A1 B1 Б(A B) .
§ 6. Рекомендации к решению задач
Предположим, что все встречающиеся в задачах этого и следующего параграфов множества являются подмножествами некоторого универсального множества U . При решении предложенных для самостоятельной работы задач ( § 7 ) полезно использовать следующие факты.
1) Изображение множеств при помощи диаграмм Эйлера-Венна, при этом множества A , B , C располагаются в в общем положении , когда A ∩ B =6 , A ∩ C =6 , B ∩ C =6 , A ∩ B ∩ C =6 .
Пример 1. Проверим равенство множеств (A B)∩C и A (B∩C) . Для этого изобразим их с помощью диаграмм Эйлера-Венна:
Рис. 6: (A B) ∩ C |
Рис. 7: A (B ∩ C) |
На рис. 6 штриховкой обозначено множество (A B) ∩ C , а на рис. 7 A (B ∩ C) . Очевидно, что это разные множества.
2) Определения и основные свойства операций над множествами, а также доказанные свойства этих операций.
Пример 2. Докажем второй дистрибутивный закон,
A (B ∩ C) = (A B) ∩ (A C),
используя определение операций объединения и пересечения для множеств и второй дистрибутивный закон для высказываний. При этом и в дальнейшем используется символ . . . . . . , который означает эквивалентность утверждений, стоящих слева и справа от него.
Решение. Пусть x U и
x A (B ∩ C) x A или x (B C)
x A или (x B и x C) (x A или x B) и
11
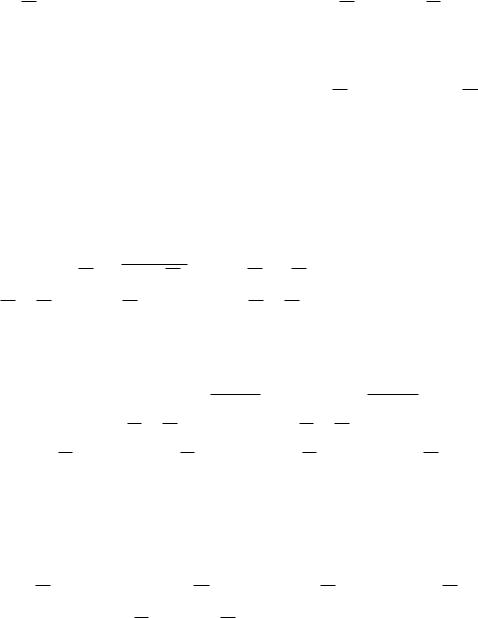
(x A или x C) (x A B) и (x A C) x (A B)∩(A C).
3)При рассмотрении равенств, содержащих символы операций 4 и
\ , полезно выразить последние через дополнение, пересечение и объединение:
A \ B = A ∩ B, A4B = (A \ B) (B \ A) = (A ∩ B) (B ∩ A). (1.1)
Первое из этих равенств непосредственно следует из определения операции \:
x A \ B x A и x / B x A и x B x A ∩ B.
Второе из равенств (1.1) является следствием первого. Пример 3. Докажем равенство
(A \ B) \ C = (A \ C) \ (B \ C).
Используем при этом первое из равенств (1.1), закон де Моргана, первый дистрибутивный закон и др.
(A ∩ C) ∩ (B ∩ C) = A ∩ C ∩ (B C) =
= (A ∩ C ∩ B) (A ∩ C ∩ C) = (A ∩ C ∩ B) = (A \ B) \ C.
Пример 4. Докажем равенство множеств
A ∩ (B4C) = (A ∩ B)4(A ∩ C) :
(A ∩ B)4(A ∩ C) = (A ∩ B ∩ A ∩ C) (A ∩ C ∩ A ∩ B) =
=(A ∩ B ∩ (A C)) (A ∩ C ∩ (A B)) =
=(A ∩ B ∩ A) (A ∩ B ∩ C) (A ∩ C ∩ A) (A ∩ C ∩ B)
На первом шаге использовалось второе из равенств (1.1), на следующем шаге использовался закон де Моргана, далее первый дистрибутивный закон для множеств. Выражения в первой и третьей скобках последнего равенства есть пустые множества, поэтому
(A ∩ B ∩ C) (A ∩ C ∩ B) = (A ∩ B ∩ C) (A ∩ C ∩ B) =
= A ∩ ((B ∩ C) (C ∩ B)) = A ∩ (B4C).
Пример 5. Докажем равенство
(A ∩ B) × (C ∩ D) = (A × C) ∩ (B × D).
Произвольным элементом множества, стоящего справа, является упорядоченная пара (x, y) . Пусть
(x, y) (A∩B)×(C∩D) (x A∩B) и (y C∩D) (x A и x B)
и (y C и y D) (x, y) (A × C) и (x, y) (B × D)(x, y) (A × C) ∩ (B × D).
12
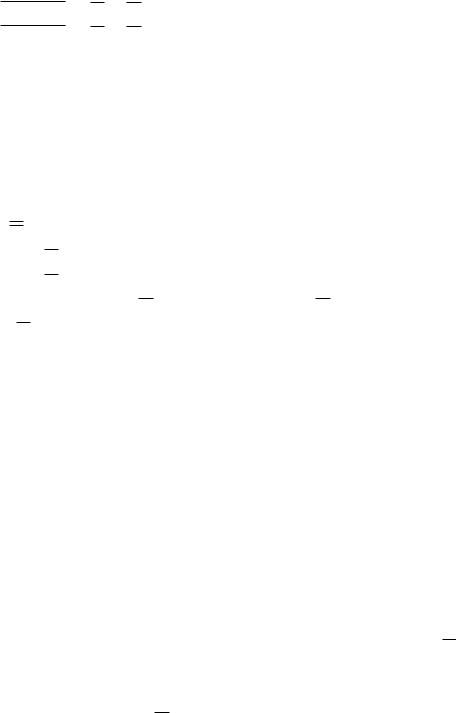
§7. Задачи и упражнения для самостоятельной работы
1.1.Доказать следующие тождества при помощи диаграмм Эйлера-
Венна:
1) A ∩ (B4C) = (A ∩ B)4(A ∩ C) ; 2) A B = (A4B)4(A ∩ B) ;
3) A \ B = A4(A ∩ B) .
1.2.Доказать следующие тождества с использованием определений операций над множествами и основных свойств операций над множествами:
1) (A ∩ B) = A B ; 2) (A B) = A ∩ B ;
3) A \ (B C) = (A \ B) ∩ (A \ C) ; 4) A \ (B ∩ C) = (A \ B) (A \ C) ; 5) A \ (A \ B) = A ∩ B ;
6) A \ B = A \ (A ∩ B) ;
7) A ∩ (B \ C) = (A ∩ B) \ (A ∩ C) = (A ∩ B) \ C ; 8) A B = (A4B) (A ∩ B) ;
9) A B = A ∩ (B \ A) ;
10)A = A ;
11)A A = U ;
12)A ∩ A = ;
13)(A ∩ B) (A B) = (A B) ∩ (A B) = A ;
14)(A B) ∩ A = A ∩ B ;
15)A ∩ (B \ A) = ;
16)(A B) \ C = (A \ C) (B \ C) ;
17)A \ (B \ C) = (A \ B) (A ∩ C) ;
18)A \ (B C) = (A \ B) \ C ;
19)A4B = B4A ;
20)A4(B4C) = (A4B)4C ;
21)A ∩ (B4C) = (A ∩ B)4(A ∩ C) ;
22)A4(A4B) = B ;
23)A B = A4B4(A ∩ B) ;
24)A \ B = A4(A ∩ B) .
1.3. Доказать с использованием определений операций над множествами и основных свойств операций над множествами:
1)A B A B = B A ∩ B = A A \ B = A B = U ;
2)A B C A C и B C ;
3)A B ∩ C A B и A C ;
4)A ∩ B C A B C ;
13

5)A B C A ∩ B C ;
6)(A \ B) B = A B A ;
7)(A ∩ B) C = A ∩ (B C) C A ;
8)A B A C B C ;
9)A B A ∩ C B ∩ C ;
10)A B A \ C B \ C ;
11)A B C \ B C \ A ;
12)A B B A ;
13)A B = A ∩ B A = B ;
14)A = B A ∩ B = и A B = U ;
15)A4B = A = B ;
16)A ∩ B = A B = A4B ;
17)A4B = C B4C = A C4A = B ;
18)A = B (A \ B) (B \ A) = .
1.4.Определить операции , ∩, \ через а) 4, ∩, б) \, 4.
1.5.Найти все подмножества множеств , { }, {x}, {1; 2}.
1.6.Сколько подмножеств из k элементов имеет множество из n элементов (k ≤ n) ?
1.7.Доказать, что (A × B) (C × D) (A C) × (B D) . При каких A , B , C и D получается равенство?
1.8.Пусть имеется последовательность множеств
X0 X1 . . . Xn . . .
Доказать, что объединение любой бесконечной подпоследовательности этих множеств совпадает с объединением всей последовательности.
1.9. Существуют ли такие множества A , B и C , что
A ∩ B 6= , A ∩ C = , (A ∩ B) \ C = ? Привести примеры. 1.10. Какие из утверждений верны для всех A , B и C ?
1)Если A B и B C , то A C ;
2)Если A B и B C , то A C ;
3)Если A ∩ B C и A C B , то A ∩ C = ;
4)Если A =6 B и B =6 C , то A =6 C ;
5)Если A (B C) и B A C , то B = .
1.11.Найти A × B , B × A , A2 , B3 , если A = {a, b, c}, B = {7, 9}.
1.12.Доказать, что имеют место следующие равенства:
1)(A B) × C = (A × C) (B × C) ;
2)(A ∩ B) × C = (A × C) ∩ (B × C) ;
3)(A \ B) × C = (A × C) \ (B × C) ;
4)A × (B \ C) = (A × B) \ (A × C) .
5)A × (B C) = (A × B) (A × C) .
14
1.13.Доказать, что (A × B) (C × D) (A C) × (B D) . При каких A , B , C и D получается равенство?
1.14.Найти геометрическую интерпретацию множеств: 1) A × B ;
2)A2 ; 3) B3 , где A = {x|x R, 0 ≤ x ≤ 1}, B = {x|x R, 1 < x < 2}.
1.15.Перечислить все элементы множества Б(A) , если:
1) A = {0, 1}; 2) A = {{1, 2}, {3}, 1}.
1.16. Доказать следующее свойство булеана: Б(A) ∩ Б(B) = Б(A ∩ B) .
1.17. Доказать, что |Б(A × B)| = 2|A×B| = 2n·m , где |A| = n ,
|B| = m .
1.18.Доказать свойства мощностей конечных множеств, приведенные на странице 8 данного пособия.
1.19.Пусть A1, . . . , Ak произвольные конечные множества. Доказать следующее равенство для мощности объединения этих множеств:
|
|
|
k |
1≤X≤ |
|
|
|
|
X |
|Ai ∩ Aj |+ |
|
|A1 A2 . . . Ak | = |Ak | − |
|
||||
|
|
|
i=1 |
i<j k |
|
+ . . .−(−1)s |
X |
≤ |
|Ai1 ∩Ai2 ∩. . .∩Ais |+. . .+. . .−(−1)k |A1∩A2∩. . .∩Ak |. |
||
1≤i |
k |
|
|
||
1 |
<...<is |
|
|
|
|
15
ГЛАВА 2. БИНАРНЫЕ ОТНОШЕНИЯ
§ 1. Определение и способы задания отношений
Подмножество ϕ множества An (ϕ An) называется n -мест- ным отношением на множестве A .
Говорят, что элементы (ai1 , . . . , ain ) находятся в отношении ϕ ,
если (ai1 , . . . , ain ) ϕ .
Одноместное отношение это просто подмножество ϕ множества A (ϕ A) . Такие отношения называют свойствами или признаками: свойство четности чисел, признак делимости на 3 и т. д.
Наиболее часто встречающимися являются двуместные или бинарные отношения. Ниже будем рассматривать только бинарные отношения, поэтому для краткости слово бинарные будем опускать. Если a и b находятся в отношении ϕ , то пишут (a, b) ϕ или aϕb .
Примерами отношений на множестве вещественных чисел являются отношения: ≤ , ≥ , < , > , = . На множестве натуральных чисел рассмотрим отношения: а) иметь один и тот же остаток от деления на 5 ; б) иметь общий делитель, отличный от 1 . На множестве плоских прямых отметим отношения параллельности, перпендикулярности, симметричности относительно начала координат и др.
Областью определения отношения ϕ на множестве A называется множество тех x A , для которых существует y A такое, что
(x, y) ϕ .
Областью значений отношения ϕ на множестве A называется множество тех значений x A , для которых существует y A такое, что (y, x) ϕ .
Рассмотрим способы задания отношений. Для задания отношений можно использовать любые способы задания множеств (например, отношение может быть задано списком пар, для которых это отношение выполняется). Отношения на конечном множестве могут быть заданы в виде таблицы (матрицы).
Таблица бинарного отношения ϕ на множестве A = (a1, . . . , am) содержит m строк и столько же столбцов, на пересечении i -й строки и j -го столбца находится элемент cij , который определяется следующим
образом: |
|
|
|
|
|
|
|
|
|
c |
|
= |
1, |
если |
(ai, aj ) ϕ, |
|
|
|
|
ij |
|
i, j = 1, m. |
|||||||
|
|
(0, |
если |
(ai, aj ) / ϕ, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Так, для бинарных отношений ϕ = {(M, ), (♦, M), (M, M), ( , M)} и ϕ−1 = {( , M), (M, ♦), (M, M), (M, )} на множестве M = {M, , ♦}
16
таблицы будут иметь следующий вид:
i j |
M |
|
♦ |
|
i j |
M |
|
♦ |
|
|
|
|
|
|
|
|
|
M |
1 |
1 |
0 |
|
M |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
♦ |
1 |
0 |
0 |
|
♦ |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
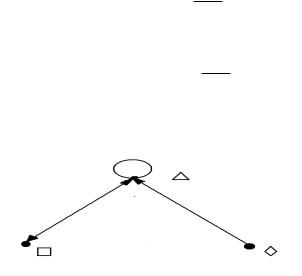
Отношение также можно задать с помощью рисунка, который называют графом. Каждому элементу xi A , i = 1, n , на плоскости ставится в соответствие точка, которую также обозначают через xi . Пара точек xi и xj соединяется направленным отрезком или кривой тогда и только тогда, когда пара точек (xi, xj ) ϕ , i, j = 1, n . Для вышезаданного отношения ϕ построим граф (см. рис. 8).
Рис. 8: Граф отношения ϕ
§ 2. Операции над отношениями
Поскольку отношения на множестве A являются подмножествами множества A2 , для них можно определить те же операции, что и для множеств: объединение, пересечение, дополнение, разность. Так отношение ≤ на множестве натуральных чисел является объединением отношений < и = . Отношение > является дополнением отношения ≤ , а отношение равенства = является пересечением отношений ≤ и ≥ на множестве действительных чисел.
Отношение ϕ−1 называется обратным к отношению ϕ , если (x, y) ϕ−1 тогда и только тогда, когда (y, x) ϕ .
Произведением отношений ϕ1 и ϕ2 на множестве A называется отношение ϕ1 ◦ϕ2 , состоящее из пар (x, y) , для которых существует элемент z A , такой, что (x, z) ϕ1 и (z, y) ϕ2 :
ϕ1 ◦ ϕ2 = {(x, y)|z (x, z) ϕ1, (z, y) ϕ2}.
Транзитивным замыканием отношения ϕ на множестве A называется отношение ϕb , которое определяется следующим образом:
17

(x, y) ϕb тогда и только тогда, когда существует цепочка из конечного числа элементов x = x1, x2, . . . , xk = y , в которой для каждой пары соседних элементов выполняется отношение ϕ : (xi, xi+1) ϕ ,
i = 1, k − 1 .
Транзитивным замыканием отношения быть сыном является отношение быть прямым потомком . Оно представляет собой объединение отношений быть сыном , быть внуком , быть правнуком и т. д. Транзитивным замыканием жить в одном городе является то же отношение.
§ 3. Свойства отношений
Отношение ϕ на множестве A называется рефлексивным, если (x, x) ϕ для x A , и антирефлексивным в противоположном случае: (x, x) / A , x A .
Примерами рефлексивных отношений являются отношения ≤ ,= и ≥ на произвольном числовом множестве.
Отношения x < y , быть сыном , быть старше являются примерами антирефлексивных отношений.
Отношение ϕ на множестве A называется симметричным, если из (x, y) ϕ следует (y, x) ϕ . Отношение ϕ называется антисимметричным, если из (x, y) ϕ и (y, x) ϕ следует x = y .
Отношения жить в одном городе , иметь общий делитель, отличный от 1 на множестве целых чисел, быть симметричным относительно оси на множестве точек плоскости являются примерами симметричных отношений. Отношения < , > , ≤ , ≥ на R , отношение включения на Б(A) являются антисимметричными.
Таблица (матрица) симметричного отношения симметрична относи-
тельно главной диагонали ( cij = cji для всех i, j = 1, m ).
Теорема. Отношение ϕ симметрично тогда и только тогда, ко-
гда ϕ−1 = ϕ . |
ϕ−1 : (x, y) ϕ |
|
Доказательство. Действительно, пусть ϕ = |
||
(y, x) ϕ−1 = ϕ , что означает симметричность |
ϕ . Наоборот, если |
ϕ |
симметрично, то (x, y) ϕ (y, x) ϕ (x, y) ϕ−1 , следовательно ϕ = ϕ−1 . Теорема доказана.
Отношение ϕ на множестве A называется транзитивным, если для любых x , y , z из множества A из (x, y) ϕ , (y, z) ϕ следует
(x, z) ϕ .
Отношения < , ≥ , = на множестве действительных чисел, отношение параллельности прямых, отношение быть соседом также являются транзитивными. Отношение перпендикулярности прямых,
18
отношение иметь общий делитель, отличный от 1 на множестве натуральных чисел свойством транзитивности не обладают.
Теорема. Если ϕ транзитивное отношение, то ϕ = ϕ . Доказательство. Из определения транзитивности замыкания следу-
ет, что ϕ ϕ . Пусть (x, y) ϕ , тогда существует |
последователь- |
|||
b |
||||
(x2, x3) ϕ , . .b |
( |
k−1 k ) |
b |
|
ность x = x1, x2, . . . , xk = y |
элементов из A таких, что (x1, x2) ϕ , |
|||
. , |
x |
, x |
ϕ , откуда в силу транзитивности ϕ полу- |
|
чаем (x, y) = (x1, xk ) ϕ . Так как (x, y) произвольная пара из ϕ , то |
||
ϕ ϕ , что и доказывает утверждение теоремы. |
b |
|
b |
§ 4. Отношение эквивалентности |
|
Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Будем говорить, что имеет место разбиение множества A на классы, если существует система {A1, A2, . . . , Ak } непустых, попарно
не пересекающихся множеств такая, что |
|
|
[ |
\ |
|
Ai 6= , A = Ak , Ai |
Aj = , i 6= j. |
(2.1) |
k
Теорема. Между совокупностью различных разбиений множества A на классы и семейством всех отношений эквивалентности на этом множестве существует взаимнооднозначное соответствие.
Доказательство. Пусть имеет место разбиение (2.1) множества A на классы. Построим отношение ϕ на множестве A по правилу: для
x, y A пара (x, y) |
|
ϕ , если элементы x , y принадлежат одному |
и тому же классу Ai |
в |
представлении (2.1) . Рефлексивность и сим- |
метричность этого отношения очевидны, покажем его транзитивность. Пусть (x, y) ϕ и (y, z) ϕ . Это означает, что x и y принадлежат классу Ak и одновременно y и z принадлежат классу Al . Если k 6= l , то получается, что элемент y принадлежит двум различным классам. Последнее противоречит тому, что Ak ∩Al = . Поэтому k = l , все элементы x , y и z принадлежат одному классу, откуда следует (x, z) ϕ . Мы доказали, что ϕ отношение эквивалентности.
Пусть ϕ произвольное отношение эквивалентности на множестве A . Построим разбиение этого множества на классы. С этой целью выберем произвольный элемент a1 A и определим класс A1 следующим образом: A1 = {x A|(a1, x) ϕ}. Класс A1 не пуст, так как в силу рефлексивности ϕ элемент a1 A1 . Выберем элемент a2 A \ A1 и построим класс A2 : A2 = {x A|(a2, x) ϕ}. Построив
19
классы A1 , A2 , . . . , Ak , выбираем элемент ak+1 A \ |
|
ik=1 Ai |
|
и класс |
||||||||
Ak+1 = {x A|(ak+1, x) ϕ}. Элемент ai |
назовем |
представителем клас- |
||||||||||
|
|
S |
|
Ai 6= . |
||||||||
са Ai, i = 1, 2, . . . Процесс продолжается до тех пор, пока A \ |
||||||||||||
|
|
|
|
|
|
|
оно явля- |
|||||
В результате получим представление A = |
|
Ai . Покажем, чтоS |
|
, i |
|
j . |
||||||
|
а именно A |
|
|
A |
j = |
6= |
||||||
ется разбиением множества A на классы, S |
|
|
i |
|
|
|
|
A , |
||||
|
|
|
|
элемент x |
|
|
||||||
Предположим, что последнее не верно: существуетT |
|
|
|
|
0 |
|
||||||
классы Ap и Aq такие, что x0 Ap , x0 Aq , p =6 q – тогда (ap, x0) ϕ , (aq , x0) ϕ . В силу симметричности и транзитивности ϕ получаем (ap, aq ) ϕ , а поэтому aq Ap , что противоречит выбору элемента aq . Теорема доказана.
Если ϕ отношение эквивалентности на A и A = S Ai , соответствующее ему разбиение множества A на классы, то множества A1 , . . . , Ak , . . . называются классами эквивалентности, а семейство {Ai} обозначается символом A/ϕ и называется фактор-множеством множества A по отношению ϕ .
Мощность множества A/ϕ называется индексом разбиения. Фактор-множество множества N по отношению иметь общий оста-
ток от деления на 5 состоит из пяти счетных классов: A1 = {1, 6, 11, . . .},
A2 = {2, 7, 12, . . .}, A3 = {3, 8, 13, . . .}, A4 = {4, 9, 14, . . .}, A5 = {5, 10, 15, . . .}.
§ 5. Отношение порядка
Отношение ϕ на множестве A называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно.
Отношение ϕ на A называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.
Говорят, что два элемента x и y из множества A сравнимы по отношению порядка ϕ , если (x, y) ϕ или (y, x) ϕ .
Множество A , на котором задано отношение порядка (строгого или нестрогого), называется полностью упорядоченным, если любые его два элемента сравнимы, и частично упорядоченным, если это не так.
Пусть множество A упорядочено отношением порядка ϕ .
Элемент x A называется наибольшим элементом множества A , если для всех y A имеет место отношение (y, x) ϕ . Наибольший элемент множества A обозначают max A .
Элемент x A называется наименьшим элементом множества A , если для всех y A имеет место отношение (x, y) ϕ . Наименьший элемент множества A обозначают min A .
Из этих определений следует, что наибольший и наименьший эле-
20
