Дискретная математика. Методичка. Кацаран

менты упорядоченного множества имеет лишь такое множество, которое упорядочено рефлексивным отношением ϕ .

Отношения ≤ и ≥ для чисел являются отношениями нестрогого порядка, а отношения < и > отношениями строгого порядка. Оба отношения полностью упорядочивают множества R и N .

Отношение включения на множестве всех подмножеств Б(A) некоторого множества A задает нестрогий частичный порядок. Отношение строгого включения задает строгий частичный порядок.

В качестве A рассмотрим множество En упорядоченных наборов длины n из нулей и единиц. Введем отношение предшествования: набор

(α1, . . . , αn) En предшествует набору (β1, . . . , βn) En , записывается как (α1, . . . , αn) (β1, . . . , βn) , если αi ≤ βi для всех i = 1, n . Построенное отношение является отношением нестрогого порядка на частично упорядоченном множестве En .

§ 6. Рекомендации к решению задач

При доказательстве равенств и включений для отношений можно пользоваться методикой, разработанной в главе 1, § 7 для множеств. При этом следует учитывать, что элементами отношения на множестве A являются упорядоченные пары (x, y) , x A , y A .

Пример 1. Докажем справедливость равенства

(ϕ ◦ ψ)−1 = ψ−1 ◦ ϕ−1.

Решение. Пусть

(x, y) (ϕ ◦ ψ)−1 (y, x) (ϕ ◦ ψ) z такое, что (y, z) ϕ и

(z, x) ψ z (z, y) ϕ−1 и (x, z) ψ−1 (x, y) ψ−1 ◦ ϕ−1.

Пример 2. Пусть ϕ1 , ϕ2 , ψ1 , ψ2 отношения на множестве A , тогда из включений ϕ1 ϕ2 , ψ1 ψ2 следует включение

ϕ−1 1 ∩ ψ1 ϕ−2 1 ∩ ψ2.

Действительно, имеет место следующая последовательность утверждений:

(x, y) ϕ−1 1 ∩ ψ1 (x, y) ϕ−1 1 и (x, y) ψ1

(y, x) ϕ1 и (x, y) ψ1 = (y, x) ϕ2 и (x, y) ψ2(x, y) ϕ−2 1 и (x, y) ψ2 (x, y) ϕ−2 1 ∩ ψ2,

которая завершает доказательство.

21

При решении задач на построение отношений с заданными свойствами и на исследование свойств заданных отношений следует иметь в виду, что то или иное свойство имеет место, если его характеристика, например (x, x) / ϕ в случае антирефлексивности, должна выполняться для всех элементов x множества A . Отсутствие того или иного свойства можно доказать, указав по крайней мере один элемент или пару элементов из A , для которых характеристика свойства не имеет места.

Пример 3. Пусть на множестве A = {α, β, γ} задано отношение ϕ = {(α, β), (β, γ), (γ, α)}. Это отношение не является рефлексивным, так как (α, α) / ϕ ; оно антирефлексивно: (α, α) / ϕ , (β, β) / ϕ , (γ, γ) / ϕ ; не симметрично (α, β) ϕ , но (β, α) / ϕ ; антисимметрично:

(α, β) ϕ и (β, α) / ϕ , (β, γ) ϕ и (γ, β) / ϕ , (γ, α) ϕ и (α, γ) / ϕ ; не транзитивно: (α, β) ϕ , (β, γ) ϕ , но (α, γ) / ϕ .

является отношением эквивалентности.

Действительно, отношение (2.2.) рефлексивно, так как

(x, x) ϕ x − x = 0 Q,

симметрично:

(x, y) ϕ x − y Q y − x Q (y, x) ϕ

и транзитивно:

(x, y) ϕ и (y, z) ϕ x − y Q и y − z Q = = x − z Q (x, z) ϕ.

§7. Задачи и упражнения для самостоятельной работы

2.1.Приведите примеры бинарных отношений на множестве целых чисел Z . Найдите для них дополнение, объединение, пересечение, разность и произведение. Постройте соответствующее множество на плоскости.

2.2.Для следующих бинарных отношений, определенных на множестве R , найти область определения, область значений и изобразить на

плоскости это отношение:

22

2.3. Построить таблицу отношения

ψ = {(m, n)|m + n = 10, m, n {1, 2, 3, 4, 5, 6}}.

Каким из свойств: рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность обладает это отношение?

2.4. Построить на множестве чисел {1, 2, 3, 4, 5, 6, 7, 8} отношение эквивалентности, соответствующее следующему разбиению этого множества на классы: а) A1 = {1, 2, 3}, A2 = {4, 5}, A3 = {6, 7, 8}; б)

A1 = {1, 3, 5, 7}, A2 = {2, 4, 6, 8}; в) Ai = {i}, i = 1, 8 . 2.5. Изобразить графы следующих отношений:

1)ϕ1 = {(a, b), (a, c), (a, d), (b, c), (b, d), (b, e), (e, b), (d, a), (e, e)};

2)ϕ2 = {(1, 2), (1, a), (a, b), (b, a), (a, 4), (3, b)}.

2.6.Показать, что ϕ◦ψ 6= ψ ◦ϕ , если ϕ = {(0, 1), (1, 0), (b, 0), (a, 1)},

ψ= {(0, 0), (0, 1)}.

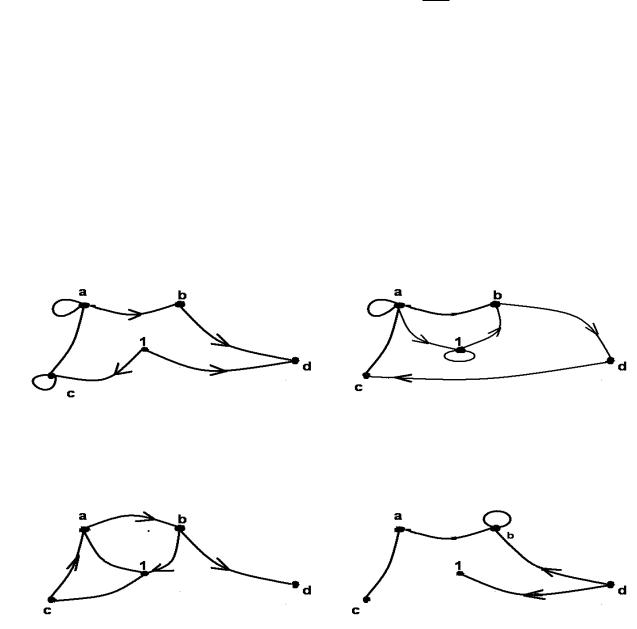
2.7. На множестве M = {a, b, c, d, 1)} заданы отношения ϕ1 , ϕ2 ,

ϕ3 , ϕ4 , графы которых изображены на рисунках 9, 10, 11, 12, соответ-

ственно. Построить ϕ−1 1 , ϕ−4 1 , ϕ1 ◦ϕ1 , ϕ1 ◦ϕ4 , ϕ1 ◦ϕ−1 1 , ϕ2 ◦ϕ−4 1 , ϕ2 ◦ϕ3 ,

ϕ−2 1 ◦ ϕ3 , ϕ−2 1 ◦ ϕ4 , ϕ−2 1 ◦ ϕ−3 1 , ϕ2 ◦ ϕ−3 1 , ϕ4 ◦ ϕ−3 1 .

23

2.8. Построить бинарное отношение:

1)рефлексивное, симметричное, не транзитивное;

2)рефлексивное, антисимметричное, не транзитивное;

3)рефлексивное, не симметричное, транзитивное;

4)не рефлексивное, антисимметричное, транзитивное;

5)не рефлексивное, симметричное, транзитивное.

2.9. Какими свойствами обладают следующие отношения:

1)ϕ1 = {(α, α), (β, γ), (γ, δ), (β, β), (δ, β)};

2)ϕ2 = {(α, α), (β, β), (γ, γ), (δ, δ), (β, δ), (α, β)};

3)ϕ3 = {(γ, δ), (δ, γ), (β, β), (β, γ), (γ, β), (α, β)};

4)ϕ4 = {(α, α), (γ, δ), (δ, β), (β, δ), (δ, γ)};

5)ϕ5 = {(α, α), (β, γ), (γ, δ), (β, β), (δ, β)}.

2.10.Сколько существует бинарных отношений на множестве A , если мощность A равна n ?

2.11.Для каких бинарных отношений справедливо равенство ϕ−1 = ϕ (по определению ϕ = A2 \ ϕ ).

2.12.Бинарным отношением между элементами множеств A и B называется любое подмножество ϕ множества A × B : ϕ A × B . Сколько существует таких бинарных отношений, если A и B конечные множества мощности n и m соответственно?

2.13.Пусть ϕ1 , ϕ2 и ψ произвольные бинарные отношения на множестве A . Показать, что имеют место равенства:

1)ψ ◦ (ϕ1 ϕ2) = (ψ ◦ ϕ1) (ψ ◦ ϕ2) ;

2)(ϕ2 ◦ ϕ1) ψ = (ϕ1 ψ) ◦ (ϕ2 ψ) ;

3)(ϕ1 ϕ2) ◦ ψ = (ϕ1 ◦ ψ) (ϕ2 ◦ ψ) ;

4)ϕ ∩ ϕ = ϕ ϕ = ϕ ;

5)(ϕ−1)−1 = ϕ ;

6)(ϕ1 ∩ ϕ2)−1 = ϕ−1 1 ∩ ϕ−2 1 .

2.14. Пусть ϕ1 , ϕ2 и ψ произвольные бинарные отношения на множестве A . Доказать, что имеют место включения:

1)(ϕ1 ∩ ϕ2) ◦ ψ (ϕ1 ◦ ψ) ∩ (ϕ2 ◦ ψ) ;

2)ψ ◦ (ϕ1 ∩ ϕ2) (ψ ◦ ϕ1) ∩ (ψ ◦ ϕ1) .

Можно ли в этих выражениях знак включения заменить знаком равенства?

2.15. Доказать, что если ϕ1 и ϕ2 симметричны, то симметричны и отношения ϕ1 ϕ2 , ϕ1 ∩ ϕ2 .

2.16.Доказать, что любое отношение ϕ , симметричное и антисимметричное одновременно, является транзитивным.

2.17.Доказать, что если ϕ1 ϕ2 , то ϕ−1 1 ϕ−2 1 ( ϕ1 и ϕ2 бинарные отношения).

24

симметрично.

2.21.Доказать, что если ϕ1 и ϕ2 рефлексивные, то (ϕ1 ∩ ϕ2)−1

рефлексивно.

2.22.Доказать, что если ϕ1 и ϕ2 рефлексивные, то ϕ1 ∩ ϕ2 рефлексивно.

2.23.Доказать, что если ϕ1 и ϕ2 антирефлексивны, то (ϕ1 ∩ϕ2)−1

антирефлексивно.

2.24.Показать, что отношение включения на множестве всех подмножеств исходного множества A является отношением нестрого порядка. Построить для этого отношения транзитивное замыкание.

2.25.Что является транзитивным замыканием отношений быть отцом , быть сыном ?

2.26.Показать, что отношение предшествования на множестве En является отношением нестрогого порядка. Что является транзитивным замыканием этого отношения?

2.27.Показать, что если ϕ отношение эквивалентности, то ϕ−1 также отношение эквивалентности.

2.28.Показать, что пересечение любой системы отношений эквивалентности на некотором множестве является отношением эквивалентности на этом множестве.

25

ГЛАВА 3. КОМБИНАТОРИКА

Настоящая глава состоит из четырех параграфов: Основные правила комбинаторики , Понятие k -выборки , Размещения, перестановки, сочетания , Формула включений и исключений . Каждый из этих параграфов содержит основные определения и теоремы по соответствующей тематике. Приводимые здесь подробные доказательства теорем являются также иллюстрацией методики решения теоретических задач разного уровня, помещенных в конце каждого раздела. Для успешного овладения материалом по теме Комбинаторика читателю рекомендуется предварительно ознакомиться с главами Множества иБинарные отношения , результаты которых используются в настоящей главе.

Комбинаторика изучает различные комбинации элементов множества. Все задачи, вопрос в которых начинается со слов Сколькими способами или Сколько , относятся к разделу математики, который называется комбинаторикой.

Итак, комбинаторика раздел математики, изучающий вопрос о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из конечного числа заданных элементов.

§ 1. Основные правила комбинаторики

Основными способами решения комбинаторных задач являются методы, которые мы будем именовать правило суммы и правило произведения .

Правило суммы. Правило суммы для двух объектов: Пусть объект a можно выбрать m способами, а объект b n способами, и существует k общих способа выбора объектов a и b , тогда один из объектов a или b можно выбрать (m + n − k) способами.

Это правило эквивалентно следующему свойству мощности:

|A B| = |A| + |B| − |A ∩ B|.

Правило суммы можно сформулировать для произвольного числа объектов. Для этого достаточно использовать формулу для мощности объединения конечного числа множеств. Для случая трех множеств формула имеет вид:

|A B C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B ∩ C|.

Правило суммы для трех объектов: Пусть объект a можно выбрать n1 способами, объект b n2 способами и объект c n3 способами, и существует n12 общих способа выбора одного из объектов a

26

и b , n13 общих способа выбора одного из объектов a и c , n23 общих способа выбора одного из объектов b и c , а также известно n123 общих способа выбора одного из объектов a , b и c , тогда число всех способов выбора одного из объектов a или b или c вычисляется по формуле:

n1 + n2 + n3 − n12 − n13 − n23 + n123.

Правило произведения. Правило произведения для двух объектов: Пусть объект a можно выбрать m способами и после каждого такого выбора объект b можно выбрать n способами, тогда выбор пары объектов a и b в указанном порядке можно осуществить m · n способами.

Данное правило произведения равносильно утверждению

|A × B| = |A||B|

(см. главу 1 Множества ).

Правило произведения является следствием теоремы о мощности прямого произведения конечного числа конечных множеств.

Правило произведения для случая произвольного числа объектов формулируется следующим образом: Пусть объект a1 можно выбрать n1 способами, a2 n2 способами, . . . , ak nk способами, причем выбор каждого из последующих объектов не зависит от выбора предыдущих объектов, тогда общее число полученных таким образом упорядоченных наборов (a1, a2, . . . , ak ) можно выбрать n1 ·n2 ·. . . nk способами.

Последнее правило применяется, если требуется выполнить одно за другим одновременно k действий, на одно из которых наложено ограничение.

§ 2. Понятие k -выборки

Пусть A = {a1, . . . , an} конечное непустое множество. Возможны два способа выбора k элементов из множества A : выбор с возвращением и выбор без возвращения. Опишем их при помощи следующей таблицы.

При реализации описанных в таблице процедур мы получаем комбинацию элементов из множества A вида [ai1 , ai2 , . . . , aik ] , которая называется k -выборкой из n элементов.

27

В случае выбора с возвращением эта комбинация может содержать повторяющиеся элементы и называется k -выборкой из n элементов с повторениями.

При реализации процедуры выбор без возвращения полученная комбинация не содержит повторяющихся элементов и называется r -выборкой из n элементов без повторений.

Выборка называется упорядоченной, если существенным является не только состав элементов в ней, но и порядок их выбора.

Две упорядоченные k -выборки считаются различными, если они отличаются либо составом элементов, либо порядком их расположения. В неупорядоченных выборках порядок расположения элементов не существенен, две различные неупорядоченные k -выборки имеют разный состав элементов.

Элементы упорядоченной выборки заключаются в круглые скобки (например (1, 2) ).

Элементы неупорядоченной выборки без повторений заключаются в фигурные скобки (например {1, 2}), а элементы неупорядоченной выборки с повторениями в квадратные скобки (например [1, 2] ).

Упорядоченные выборки (3, 2) и (2, 3) считаются различными, хотя и составлены из одних и тех же элементов. Для тех же самых элементов2 и 3 неупорядоченные выборки {3, 2} и {2, 3} (или [3, 2] и [2, 3] ) считаются одной и той же.

Рассмотрим множество, которое содержит три элемента A = {1, 2, 3}. Составим из элементов этого множества всевозможные 2 -выборки.

Упорядоченные 2-выборки без повторений: (1, 2) , (2, 1) , (1, 3) , (3, 1) ,

(2, 3) , (3, 2) .

Упорядоченные 2-выборки с повторениями: (1, 2) , (2, 1) , (1, 3) , (3, 1) ,

(2, 3) , (3, 2) , (1, 1) , (2, 2) , (3, 3) .

Неупорядоченные 2-выборки без повторений: {1, 2}, {1, 3}, {2, 3}. Неупорядоченные 2-выборки с повторениями: [1, 2] , [1, 3] , [2, 3] ,

[1, 1] , [2, 2] , [3, 3] .

В следующих параграфах будут даны формулы для подсчета количества k -выборок из n элементов.

§ 3. Размещения с повторениями и без повторений. Перестановки без повторений

Размещениями из n элементов по k называются упорядоченные k -выборки из n элементов.

Размещениями без повторений из n элементов по k называются упорядоченные k -выборки из n элементов без повторений. Их число

28

обозначается Akn .

Размещениями с повторениями из n элементов по k называются упорядоченные k -выборки из n элементов с повторениями. Их число

˜k

обозначается An .

Перестановками из n элементов называются размещения без повторений из n элементов по n . Их число обозначается P (n) .

Теорема. Имеют место следующие равенства:

Доказательство. Пусть A = {a1, . . . , an} произвольное множество, (ai1 , ai2 , . . . , aik ) упорядоченная k -выборка без повторений, составленная из элементов множества. Она представляет собой набор длины k вида (ai1 , ai2 , . . . , aik ) , в котором

k[−1

ai1 A, ai2 A \ {ai1 }, . . . , aik A \ {ail }.

l=1

Число таких наборов равно мощности прямого произведения множеств

k[−1

A × (A \ {ai1 }) × . . . × (A \ {ail }).

l=1

В силу теоремы о мощности прямого произведения имеем:

k[−1

Akn = |A × (A \ {ai1 }) × . . . × (A \ {ail }| =

l=1

k[−1

= |A||(A \ {ai1 })| . . . |A \ {ail }| = n(n − 1)...(n − k + 1).

l=1

Умножим и разделим последнее выражение на (n−k)! и получим первое равенство из (3.1).

Размещения с повторениями из элементов множества A по k представляют собой упорядоченный набор (ai1 , ai2 , . . . , aik ) , в котором каждый из элементов ail , l = 1, k может быть выбран n способами. В силу правила произведения указанный набор может быть выбран nk способами, что и доказывает второе из равенств (3.1).

Третье получается из первого при k = n . Теорема доказана.

29

§ 4. Сочетания с повторениями и без повторений

Сочетаниями из n элементов по k называются неупорядоченные k -выборки из n элементов.

Сочетаниями без повторений из n элементов по k называются неупорядоченные k -выборки из n элементов без повторений. Их число обозначается Cnk .

Сочетаниями с повторениями из n элементов по k называются неупорядоченные k -выборки из n элементов с повторениями. Их число обозначается Hnk .

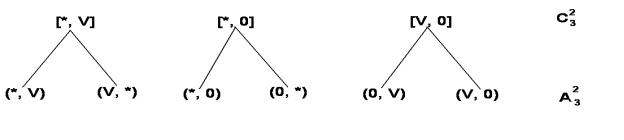
Доказательство. Прежде чем доказать равенство для Cnk в общем случае, рассмотрим пример. Пусть A = {, , 0}, тогда выборки [ , ] , [ , 0] , [ , 0] представляют собой сочетания без повторений по 2, составленные из элементов множества A . Из каждого сочетания можно получить, производя в нем перестановку элементов, размещения без повторений по 2 из элементов множества A . Этот процесс изобразим в виде следующей схемы (см. рис. 13).

Рис.13

На основании вышеизложенного имеем равенство: A23 = C32 P (2) . Аналогичная ситуация имеет место в общем случае: чтобы полу-

чить все Akn размещений, нужно получить всевозможные сочетания из n элементов по k (их число равно Cnk ), затем в каждом из сочетаний сделать всевозможные перестановки . Число перестановок, которые можно получить из одного сочетания длины k , равно P (k) . Очевидно, что из разных сочетаний без повторений не могут получиться одинаковые перестановки. Поэтому Akn = Cnk P (k) , откуда следует первое из равенств (3.2).

Перейдем к доказательству второго равенства (3.2). Введем обозначения: Ink множество сочетаний с повторениями из чисел {1, 2, . . . , n}

30