
Лин. програм. учеб. пособие (Азарнова Т. В
.).pdfЛ и нейн ое п р огр а м м и р ов а ни е
§1. О бщ аяп о ст ан о в к а задачи лин ейн о го п ро грам м иро в ан ия
Графическ о е реш ен ие задач лин ейн о го п ро грам м иро в ан ия
За да чейли н ейн огоп р огр а м м и р ов а н и я (ЗЛ П ) н а зы в а ет с я за да ча н а хо-
ж ден и я в в ект ор н ом |
п р ос т р а н с т в е Rn т а когов ект ор а |
x* , кот ор ы йобес п ечи - |
|||||||||
в а ет оп т и м а льн ое |
(м а кс и м а льн ое |
и ли |
м и н и м а льн ое) |
зн а чен и е ли н ейн ой |
|||||||
|
n |
|
|
|
|
|
|
|
|
|
|
фун кци и |
( ) = å j x j c и Lп рxи |
эт ом |
п р и н а длеж и т |
н екот ор ой |
обла с т и |
||||||
|
j=1 |
|
|
|
|
|
|
|
|
|
|
Ω Í Rn , за да н н ойли н ейн ы м и |
огр а н и чен и ям и |
|
|
|
|
||||||
|
|
|
n |
|
£ (³ =)bi |
|
|
|
|
|
|
|
|
|
åaij x j |
i =1 |
m |
, |
, |
,..., |
|||
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
j ³ |
(£ |
тxр ебов а ни я н а зна к) |
нет= ,..., n. 1 |
j, |
|||||
Ф ункцию L(x) на зы ва ю т |
целевой ф ункцией ЗЛ П , ее оп т има льное зна - |
||||||||||
чение обозна ча ю т |
L* . |
М нож ест во Ω Í Rn |
на зы ва ю т |
доп уст имы м мно- |
|||||||
ж ест вом, |
его элемент ы |
- доп уст имы мивект ор а ми, а вект ор |
x * - |
р ешени- |
|||||||
ем за да чи(оп т има льной т очкой). |
|
|
|
|
|
|
|
||||
П р еж де чем р а с с м а т р и в а т ь м ет оды |
р еш ен и я общ ейза да чи ли н ейн ого |
||||||||||
п р огр а м м и р ов а н и я в Rn , р а с с м от р и м а лгор и т м гр а фи чес когом ет ода , кот о- р ы йи с п ользует с я в R2 для р еш ен и я за да чи с ледующ егов и да :
c1x1 + c2x2 ® max(min)
ai1x1 + ai2x2 £ (³, =)bi , |
i =1,..., m |
|
|||
x1 x2 ³ |
,(£, |
0 |
|
зна к) . на |
т р ебова ни |
1. П ос т р оен и е доп ус т и м огом н ож ес т в а . |
|
|
|||
За м ет и м , чт о ка ж дое огр а н и чен и е за да чи оп р еделяет н екот ор ую п олуп лос - |
|||||
кос т ь (в с луча е н ер а в ен с т в а ) и ли |
п р ям ую (в |
с луча е р а в ен с т в а ). Доп ус т и м ы м |
|||
м н ож ес т в ом яв ляет с я п ер ес ечен и е эт и х п олуп лос кос т ейи п р ям ы х. Та ки м |
об- |
||||
р а зом , для п ос т р оен и я доп ус т и м огом н ож ес т в а н уж н о: |
|
||||
а ) для ка ж догоогр а н и чен и я н а р и с ов а т ьп р ям ую, с оот в ет с т в ующ ую р а - |
|||||
в ен с т в у ai1x1 + ai2x2 = bi, |
i = 1,..., m ; |
|
|
|
|
б) ес ли огр а н и чен и е за да ет с я н ер а в ен с т в ом |
в и да ai1x1 + ai2x2 £ bi |
и ли |
|||
ai1x1 + ai2x2 ³ bi , т о оп р едели т ь п олуп лос кос т ь, |
за да в а ем ую да н н ы м н ер а - |
||||
в ен с т в ом . Эт о легко с дела т ь, ес ли п одс т а в и т ь в н егокоор ди н а т ы т очки , н е |
|||||
р а с п олож ен н ойн а с оот в ет с т в ующ ейп р ям ой. Ес ли н ер а в ен с т в оока зы в а ет с я с п р а в едли в ы м , т ов ы бр а т ьп олуп лос кос т ь, с одер ж а щ ую да н н ую т очку, в п р о- т и в н ом с луча е - в ы бр а т ьп р от и в оп олож н ую п олуп лос кос т ь.
в ) н а йт и п ер ес ечен и е п олучен н ы х п олуп лос кос т ейи п р ям ы х.
2. Реш ен и е за да чи |
п ут ем а н а ли за доп ус т и м огом н ож ес т в а и п ов еден и я |
целев ойфун кци и н а эт ом |
м н ож ес т в е. |
3
Л и нейное п р огр а м м и р ов а ни е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
а ) |
П ус т ь доп ус т и м ое м н ож ес т в оока за лос ь |
п ус т ы м . Дела ет с я в ы в од: |
|||||||||||||||
за да ча р еш ен и йн е и м еет , п ос кольку н ет н и одн ойдоп ус т и м ойт очки . |
|
|||||||||||||||||
|
б) П ус т ь доп ус т и м ое м н ож ес т в о ока за лос ь н е п ус т ы м . Вы бр а т ь дв а |
|||||||||||||||||
п р ои зв ольн ы х чи с ла |
d1 и |
d2 , |
d1 > d2 . |
На р и с ов а т ь ли н и и ур ов н я целев ой |
||||||||||||||
фун кци и , |
с оот в ет с т в ующ и е |
|
в ы бр а н н ы м |
кон с т а н т а м , |
т .е. |
п р ям ы е в и да |
||||||||||||
c1x1 + c2x2 = d1 |
и |
c1x1 + c2x2 = d2 (эт оп а р а ллельн ы е п р ям ы е, |
в с е т очки кот о- |
|||||||||||||||
р ы х обес п ечи в а ют зн а чен и я целев ойфун кци и , р а в н ы е с оот в ет с т в ен н о d1 |
и |
|||||||||||||||||
d2 ). |
За фи кс и р ов а т ь н а п р а в лен и е ув ели чен и я зн а чен и йцелев ойфун кци и |
от |
||||||||||||||||
п р ям ойс |
п р а в ойча с т ью, р а в н ой d2, |
кп р ям ойс п р а в ойча с т ью, р а в н ой d1. |
||||||||||||||||
П ер едв и га т ьп р ям ую |
c1x1 + c2x2 = d |
п а р а ллельн ос а м ойс ебе п одоп ус т и м о- |
||||||||||||||||
м ум н ож ес т в ув обозн а чен н ом |
н а п р а в лен и и (в |
п р от и в оп олож н ом |
н а п р а в ле- |
|||||||||||||||
н и и ) |
до п олучен и я м а кс и м а льн ого зн а чен и я |
d* |
(м и н и м а льн ого зн а чен и я |
|||||||||||||||
d*), |
п р и |
кот ор ом |
п р ям а я c x |
1 |
+ c x |
2 |
= d п ер ес ека ет доп ус т и м ое м н ож ес т в о. |
|||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||
За фи кс и р ов а т ь н а |
гр а фи ке т очки доп ус т и м огом н ож ес т в а , обес п ечи в а ющ и е |
|||||||||||||||||
м а кс и м а льн ое (м и н и м а льн ое) зн а чен и е целев ойфун кци и и ли |
убеди т ьс я, чт о |
|||||||||||||||||
т а ки х т очекн ет . Ес ли |
доп ус т и м ое м н ож ес т в оогр а н и чен о(яв ляет с я м н ого- |
|||||||||||||||||
угольн и ком ), т ов озм ож н ы |
дв а р а зли чн ы х от в ет а : р еш ен и е еди н с т в ен н ои ли |
|||||||||||||||||
р еш ен и йбес чи с лен н ое м н ож ес т в о. |
|
П р и |
еди н с т в ен н ом |
р еш ен и и |
н а гр а фи ке |
|||||||||||||
за фи кс и р ов а н а |
еди н с т в ен н а я т очка (в ер ш |
и н а |
м н огоугольн и ка), яв ляющ а яс я |
|||||||||||||||
п ер ес ечен и ем |
н екот ор ы х п р ям ы х. |
Необходи м о в ы п и с а т ь с оот в ет с т в ующ и е |
||||||||||||||||
ур а в н ен и я п р ям ы х и , |
р еш и в |
с и с т ем у п олучен н ы х ур а в н ен и й, н а йт и т очку - |
||||||||||||||||
р еш ен и е за да чи . В с луча е бес чи с лен н огом н ож ес т в а р еш ен и йп олучен от р е-
зокп р ям ой, в с е т очки кот ор огообес п ечи в а ют |
м а кс и м а льн ое зн а чен и е целе- |
||||||||||
в ойфун кци и . Ср еди эт и х т очекес т ьв ер ш |
и н ы |
м н огоугольн и ка. К оор ди н а т ы |
|||||||||
в ер ш и н |
от ы с ки в а ют с я т а к, ка кука за н ов |
п р еды дущ ем |
с луча е. Ес ли |
доп ус - |
|||||||
т и м ое м н ож ес т в о н е огр а н и чен о, |
т о в озм ож н ы т е ж е дв е с и т уа ци и , чт ои в |
||||||||||
с луча е огр а н и чен н огом н ож ес т в а , |
и , |
кр ом е т ого, в озм ож ен с луча йот с ут с т - |
|||||||||
в и я р еш ен и йи з-за н еогр а н и чен н ос т и |
зн а чен и йцелев ойфун кци и н а доп ус т и - |
||||||||||
м ом м н ож ес т в е. |
|
|
|
|
|
|
|
|
|
|
|
И з а н а ли за гр а фи чес когом ет ода |
р еш ен и я м ож н ос дела т ь в ы в оды , ко- |
||||||||||
т ор ы е |
яв ляют с я с п р а в едли в ы м и и |
для за да ч и з Rn. |
|
|
|
||||||
1. |
Доп ус т и м ое м н ож ес т в о за да чи |
ли н ейн ого п р огр а м м и р ов а н и я, ес ли |
|||||||||
он о н е п ус т о, яв ляет с я м н огогр а н н ы м |
огр а н и чен н ы м |
и ли |
н еогр а н и чен н ы м |
||||||||
в ы п уклы м м н ож ес т в ом . |
|
|
|
|
|
|
|
|
|
|
|
2. |
Ес ли в за да че ес т ь р еш |
ен и е (оп т и м а льн а я т очка), |
т ос р еди |
в ер ш и н |
|||||||
доп ус т и м ого м н ож ес т в а |
т а кж е |
ес т ь р еш ен и е. Ч а с т ь оп т и м а льн ы х т очек |
|||||||||
м ож н ои с ка т ь, п ер еби р а я т ольков ер ш и н ы доп ус т и м огом н ож ес т в а . |
|
||||||||||
П р ои ллюс т р и р уем |
р а с с м от р ен н ы йгр а фи чес ки йм ет од н а п р и м ер а х. |
||||||||||
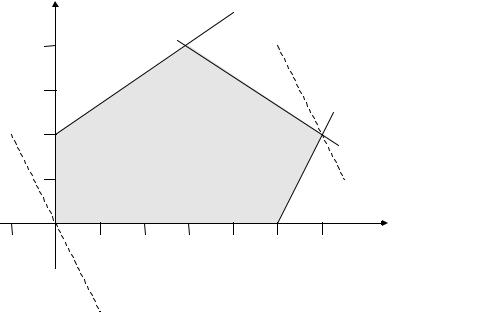
П р и м ер 1. Реш и т ьгр а фи чес ки с ледующ ую за да чули н ейн огоп р огр а м - м и р ов а н и я
4x1 + 2x 2 → max
4
|
Л и нейн ое п р огр а м м и р ов а ни е |
2x1 + 3x 2 ≤ 18 |
(1) |
− x1 + 3x 2 ≤ 9 |
(2) |
2x1 - x2 £10 |
(3) |
x1 ³ 0, x2 ³ 0. |
|
Реш ен и е. Ст р ои м обла с т ь доп ус т и м ы х р еш ен и йв с оот в ет с т в и и с ш а - гом 1 оп и с а н н огов ы ш е а лгор и т м а . В р езульт а т е п олучи м в ы п уклы йм н огоугольн и к (р и с 1.)
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
d=28 |
|
X2 |
|
|
3 |
|
|
|
|
.X |
*max |
|
|
|
|
|
|
|
|
X1 |
|
|
d=0 |
|
Ри с .1 |
|
|
|
|
|
|
Следуя п ун кт у 2 р а с с м от р ен н ого а лгор и т м а , с т р ои м ли н и и ур ов н я целев ой фун кци и 4x1 + 2x 2 = d и фи кс и р уем н а п р а в лен и е ув ели чен и я зн а чен и я целе- в ойфун кци и п р и п ер еходе от одн ойли н и и ур ов н я кдр угой. П ер ем ещ а я п р я-
м ую |
4x1 + 2x 2 = d п а р а ллельн о с а м ойс ебе в н а йден н ом |
н а п р а в лен и и , п ока |
|||||
он а |
будет с охр а н ят ь общ и е т очки |
с доп ус т и м ой обла с т ью, н а йдем , чт о в |
|||||
кр а йн ем |
в озм ож н ом |
п олож ен и и ли н и я ур ов н я п р ойдет |
чер ез т очку xmax* . |
||||
Эт ом у п олож ен и ю ли н и и ур ов н я и |
с оот в ет с т в ует d = dmax . Для н а хож ден и я |
||||||
коор ди н а т т очки xmax* |
н еобходи м ор еш и т ьс и с т ем уур а в н ен и й: |
||||||
|
|
|
|
ì2x1 |
+ 3x2 = 18 |
. |
|
|
|
|
|
í |
- x2 = 10 |
|
|
|
|
|
|
î2x1 |
|
|
|
|
В р езульт а т е п олучи м |
и с ком ое оп т и м а льн ое р еш ен и е X max* = (6,2) с |
|||||
зн а чен и ем |
целев ойфун кци и |
L*max = 28. |
|
|
|||
|
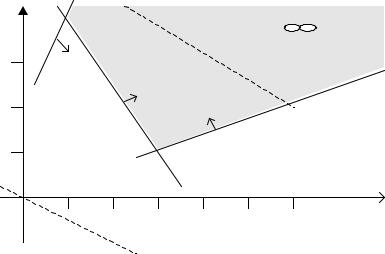
П р и м ер 2. Реш и т ьгр а фи чес ки с ледующ ую за да чу: |
|
|||||
5
Л и нейное п р огр а м м и р ов а ни е
2x1 + 4x2 ® max
3x1 + 2x2 ³ 11 |
(1) |
− 2x1 + x2 ≤ 2 |
(2) |
x1 − 3x2 ≤ 0 |
(3) |
x1 ³ 0, x2 ³ 0.
Реш ен и е. П ер в ы йэт а п - п ос т р оен и е доп ус т и м ойобла с т и - в ы п олн яет с я т а к- ж е ка к и в п р еды дущ ей за да че. В р езульт а т е п олуча ем н еогр а н и чен н ую м н огогр а н н ую обла с т ь.
1 |
Z*max= + |
||
|
|||
2 |
3 |
d=22 |
|
X2 |
|||
|
|
||
|
.X*min |
|
|
|
X1 |
Ри с . 2. |
|
|
d=0 |
|
|
На в т ор ом |
эт а п е р еш ен и я - п а р а ллельн ом |
п ер ем ещ ен и и ли н и и ур ов н я в н а - |
п р а в лен и и |
в озр а с т а н и я целев ойфун кци и |
ус т а н а в ли в а ем , чт о т а кое п ер ем е- |
щ ен и е м ож н оп р ои зв оди т ь н еогр а н и чен н о. |
Следов а т ельн о, |
целев а я фун кци я |
|||||
н еогр а н и чен н а |
с в ер ху, т .е. Lmax = ¥ , а |
с а м а |
за да ча ли н ейн огоп р огр а м м и р о- |
||||
в а н и я н ер а зр еш |
и м а . За м ет и м , чт оес ли |
п р и |
т ех ж е и с ходн ы х да н н ы х т р ебов а - |
||||
лос ь бы |
целев ую фун кци ю м и н и м и зи р ов а т ь, т о п олучи ли |
бы оп т и м а льн ое |
|||||
р еш ен и е в т очке xmin* |
= ( 31,) с L*min = 10. |
|
|
|
|||
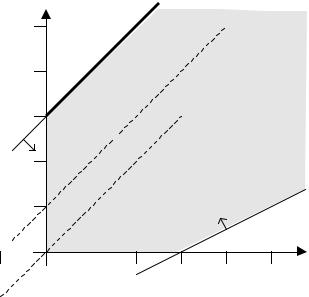
П р и м ер |
3. Реш и т ьза да чу |
|
|
|
|
||
|
|
|
- x1 + x 2 ® max |
|
|||
|
|
|
- x1 + x 2 £ 3 |
|
(1) |
|
|
|
|
|
x1 - 2x2 £ 3 |
|
(2) |
|
|
|
|
|
x1 ³ 0, x2 ³ 0. |
|
|||
|
Реш ен и е. |
Доп ус т и м а я обла с т ьв |
да н н ойза да че и м еет в и д |
||||
6
Л и нейн ое п р огр а м м и р ов а ни е
|
Z*max=3 |
|
|
|
X2 |
max |
|
X2 |
|
. |
|
X1max. |
|
d=1 |
|
1 |
|
|
|
|
|
d=0 |
|
|
|
2 |
X1 |
|
|
|
|
ри с 3.
Из р и с ун ка в и дн о, чт одоп ус т и м ое м н ож ес т в он еогр а н и чен н о. Л и н и и ур ов н я
целев ойфун кци и п а р а ллельн ы п р ям ой- x1 + x2 |
= 3, с оот в ет с т в ующ ей п ер - |
||
в ом у огр а н и чен и ю. П ер ем ещ а я ли н и и ур ов н я |
в |
н а п р а в лен и и в озр а с т а н и я |
|
целев ой фун кци и , п олуча ем , |
чт о ли н и я ур ов н я с |
м а кс и м а льн о в озм ож н ы м |
|
зн а чен и ем целев ойфун кци и |
с ов п а да ет с п р ям ой - x1 + x2 = 3. Та ки м обр а - |
||
зом , целев а я фун кци я дос т и га ет с в оегом а кс и м а льн огозн а чен и я L*max = 3 в о
в с ех т очка х луча , в ы ходящ егои з т очки |
x1max = ( 03,). За да ча |
и м еет |
бес чи с - |
|||||||||
лен н ое м н ож ес т в ор еш ен и й. |
|
Для т огочт обы |
в ы п и с а т ьр еш ен и е в общ ем |
в и - |
||||||||
де, в озьм ем |
н а |
луче ещ е одн ут очку xmax2 |
= ( |
14,). У р а в н ен и е луча за п и с ы в а ет - |
||||||||
с я с ледующ и м |
обр а зом : |
( |
) |
1 x 1 x2λ λ x[ ,λ∞0 ). , |
|
|
|
|||||
|
|
|
|
* |
+ |
= − |
||||||
|
|
|
|
max |
|
|
max |
max |
|
|
|
|
Та ки м |
обр а зом , |
любое р еш ен и е |
да н н ой за да чи за п и с ы в а ет с я |
в |
в и де |
|||||||
xmax* |
( |
λ) λ |
λ[ ,∞0). =, |
|
,3+ |
|
|
|
|
|
|
|
|
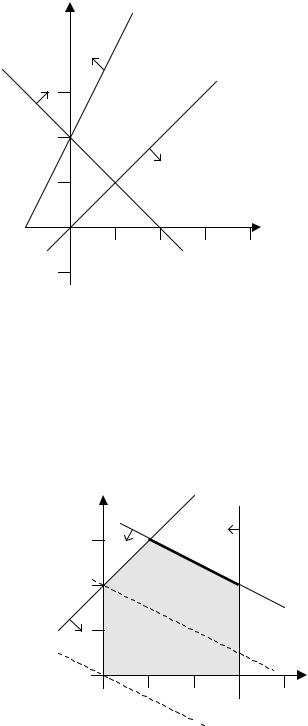
П р и м ер 4. Реш и т ьгр а фи чес ки за да чу |
|
|
|
|
|||||||
|
|
|
|
|
|
3x1 + 3x2 ® min |
|
|
|
|||
|
|
|
|
|
|
x1 + x2 ³ 2 |
(1) |
|
|
|
||
|
|
|
|
|
|
- 2x1 + x2 ³ 2 |
(2) |
|
|
|
||
|
|
|
|
|
|
x1 - x2 ³ 0 |
(3) |
|
|
|
||
|
Реш ен и е. |
Доп ус т и м ое м н ож ес т в ода н н ойза да чи п ус т о. Эт ов и дн ои з |
||||||||||
с ледующ егор и с ун ка |
|
|
|
|
|
|
|
|
||||
7
Л и нейное п р огр а м м и р ов а ни е
|
|
2 |
1 |
X2 |
|
|
X2 |
3 |
|
|
|
|
|
X1 |
Ри с 4.
П оэт ом уда н н а я за да ча н ер а зр еш и м а .
Пр и м ер 5. Реш и т ьгр а фи чес ки за да чу
x1 + 2x 2 ® max
−x1 + x2 ≤ 2 (1) x1 + 2x2 ≤ 7 (2)
£ x1 £ x2 |
³0 |
, 3 |
Реш ен и е. Доп ус т и м ы м м н ож ес т в ом |
в да н н ойза да че яв ляет с я в ы п ук- |
|
лы йм н огогр а н н и к(р и с . 5).
|
X1max |
|
. |
X2 |
.X2max |
|
|
|
d=4 |
|
X1 |
|
d=0 |
|
Ри с .5 |
|
Л и н и и ур ов н я целев ой фун кци и п а р а ллельн ы |
п р ям ой, с оот в ет с т в ую- |
|
щ ей огр а н и чен и ю |
(2). П р ов одя р а с с уж ден и я, а н а логи чн ы е р а с с уж ден и ям в |
|
п р и м ер е 3, п олучи м , чт о целев а я фун кци я дос т и га ет |
с в оегом а кс и м а льн ого |
|
зн а чен и я L*max = 7 |
в ов с ех т очка х от р езка , с оеди н яющ егот очки x1max = ( 13,) и |
|
8
Л и нейн ое п р огр а м м и р ов а ни е
xmax2 |
= ( |
32,). За да ча и м еет |
бес чи с лен н ое м н ож ес т в о р еш ен и й, |
кот ор ое за п и - |
||||||||
с ы в а ет с я с ледующ и м |
обр а зом |
|
|
|
|
|
|
|
|
|||
|
|
|
* |
( |
) |
1 x |
x2 |
1 λλx [ |
1,]0.λ |
+, |
= − |
|
|
|
|
max |
|
|
max |
max |
|
|
|
|
|
Та ки м |
обр а зом , |
любое |
р еш ен и е |
да н н ой |
за да чи |
и м еет |
в и д |
|||||
xmax* |
( |
) |
λ [ λ1,]0. |
− |
=, |
+ 13, |
2 |
|
|
|
|
|
|
|
Задачи длясам о ст о ят ельн о го реш ен ия |
|
|
||||||||
1.Реш и т ьгр а фи чес ки : |
|
|
|
|
|
|
|
|
|
|||
1) x1 - 2x2 ® max |
|
|
2) x1 + 3x2 ® max |
|
|
|
|
|||||
x1 + x2 ³ 2 |
|
|
|
x1 - x2 ³ 0 |
|
|
|
|
||||
x1 - x2 £1 |
|
|
|
2x1 + x2 £ 2 |
|
|
|
|
||||
x1 - 2x2 £ 0 |
|
|
|
x1 - x2 £ 1 |
|
|
|
|
||||
x1 ³ 0, x 2 ³ 0. |
|
|
|
x1 ³ 0, x2 ³ 0 |
|
|
|
|
||||
3) 5x1 + 3x2 ® max |
|
|
|
4) 2x1 + 3x2 ® max |
|
|
|
|
||||
3x1 + 5x2 £15 |
|
|
|
3x1 + 2x2 £ 6 |
|
|
|
|
||||
5x1 + x2 £10 |
|
|
|
x1 + x2 ³ 6 |
|
|
|
|
||||
x1 ³ 0, x2 ³ 0 |
|
|
|
x1 ³ 0, x2 ³ 0 |
|
|
|
|
||||
5) 2x1 + 3x2 ® min |
|
|
|
6) x1 + x2 ® max |
|
|
|
|
||||
3x1 + 2x2 ³ 6 |
|
|
|
x1 + 2x2 £10 |
|
|
|
|
||||
x1 + 4x2 ³ 4 |
|
|
|
x1 + 2x2 ³ 2 |
|
|
|
|
||||
|
|
|
|
|
|
2x1 + x2 £10 |
|
|
|
|
||
x1 ³ 0, x2 £ 0 |
|
|
|
x1 ³ 0. |
|
|
|
|
|
|||
2. О п р едели т ь п р ом еж ут ки зн а чен и й λ , п р и кот ор ы х р еш |
ен и е будет |
с ов п а - |
||||||||||
да т ьс одн ойи т ойж е в ер ш и н ойобла с т и доп ус т и м ы х р еш ен и й. В ка ки х п р о-
м еж ут ка х за да ча н е и м еет |
р еш ен и й? П р и ка ки х зн а чен и ях λ будет бес чи с - |
лен н ое м н ож ес т в ор еш ен и й? |
|
1) 2x1 + λx2 ® max |
2) - x1 + λx2 ® max |
- x1 + x2 £ 3 |
- x1 + x2 £ 2 |
x1 + 2x 2 £ 12 |
x1 - 2x2 £ 3 |
3x1 - x 2 £ 15 |
|
x1 ³ 0, x2 £ 0 |
x1 ³ 0, x2 £ 0 |
3) 2x1 + x2 ® max |
3) x1 + 2x2 ® max |
x1 - 2x2 £ 4 |
2x1 + x 2 ³ 9 |
x1 - x2 £ 6 |
x1 - 3x 2 £ 1 |
9
Л и нейное п р огр а м м и р ов а ни е |
|
λx1 + x2 £ 3 |
λx1 - x 2 £ -2 |
x1 ³ 0, x2 £ 0 |
x1 ³ 0, x2 £ 0 . |
3. П р и в ес т и п р и м ер |
гр а фи чес койи н т ер п р ет а ци и и с ос т а в и т ь н а ос н ов а н и и |
п олучен н ого чер т еж а |
м а т ем а т и чес кую за п и с ь за да чи , обла да ющ ейс ледую- |
|||||||
щ и м и с в ойс т в а м и : |
|
|
|
|
|
|
|
|
1) |
и м еет с я еди н с т в ен н ое оп т и м а льн ое р еш ен и е для за да чи |
н а м и н и м ум |
||||||
|
и для за да чи н а м а кс и м ум ; |
|
|
|
|
|
||
2) |
м а кс и м а льн ое зн а чен и е целев а я фун кци я дос т и га ет в бес чи с лен н ом |
|||||||
|
м н ож ес т в е т очек, а м и н и м а льн ое зн а чен и е в еди н с т в ен н ойт очке; |
|||||||
3) |
н а м и н и м ум |
за да ча н ер а зр еш |
и м а и з-за н еогр а н и чен н ос т и целев ой |
|||||
|
фун кци и , а |
м а кс и м а льн ое зн а чен и е дос т и га ет с я в |
еди н с т в ен н ойт оч- |
|||||
|
ке; |
|
|
|
|
|
|
|
4) |
н а м а кс и м |
ум |
и н а м и н и м ум |
за да ча н ер а зр еш и м а |
и з-за |
н еогр а н и - |
||
|
чен н ос т и целев ойфун кци и ; |
|
|
|
|
|
||
5) |
м и н и м а льн ое зн а чен и е целев ой фун кци и дос т и га ет с я в |
бес чи с лен - |
||||||
|
н ом м н ож ес т в е т очек, и з кот ор ы х т олькоодн а яв ляет с я в ер ш и н ой. |
|||||||
§2. Разн ы е фо рм ы зап иси задачи лин ейн о го п ро грам м иро в ан ия |
||||||||
В §1 п р и в еден а общ а я п ос т а н ов ка за да чи |
ли н ейн огоп р огр а м м и р ов а н и я |
|||||||
(ЗЛ П ). Ч а с т одля удобс т в а и с с ледов а н и я и п р и |
п ос т р оен и и м ет ода р еш |
ен и я |
||||||
фи кс и р ует с я т а и ли и н а я за п и с ьза да чи . Та к, ча с т ои с п ользует с я за да ча в |
с ле- |
|||||||
дующ ейфор м е:
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
åc j x j |
® max |
|
|
|
|
||
|
|
|
j=1 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
å |
|
j |
£ij i |
= ,..., m 1 |
i |
b a x |
|
||
|
j=1 |
|
j ³ |
|
= ,...x, n .1 |
j0, |
|
|
|
|
|
|
|
|
|
|
|
||||
Та ка я фор м а |
за п и с и ЗЛ П н а зы в а ет с я с т а н да р т н ойи ли с и м м ет р и чн ойфор м ой |
|||||||||
за да чи ли н ейн ого п р огр а м м и р ов а н и я. К р ом е т ого, |
в ы деляют |
ка н он и чес кую |
||||||||
фор м уза п и с и |
ЗЛ П : |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åc j x j |
® max |
|
|
|
|
||
|
|
|
j=1 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
å |
j |
ij i |
i |
|
= = ,..., m³,1 |
i, 0 |
b b a x |
||
|
j=1 |
|
j ³ |
|
= ,...x, n .1 |
j0, |
|
|
|
|
|
|
|
|
|
|
|
||||
Вн е за в и с и м ос т и от т ого, |
|
ка кза п и с а н а |
и с ходн а я за да ча , он а |
м ож ет |
||||||
бы т ьп ер еп и с а н а в любойж ела т ельн ойфор м е. |
П р и |
эт ом |
с ущ ес т в уют |
п р а в и - |
||||||
ла , п озв оляющ и е эт ос дела т ьэкв и в а лен т н ы м обр а зом . С эт ойцелью обс уди м
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л и нейн ое п р огр а м м и р ов а ни е |
|
||||||||||||||
п он ят и е экв и в а лен т н ы х за да ч оп т и м и за ци и . Сущ ес т в ует с т а н да р т н ое оп р еде- |
|
|||||||||||||||||||||||||||||
лен и е: две оп т имиза ционны е за да чина зы ва ю т |
ся эквива лент ны ми, |
еслиони |
|
|||||||||||||||||||||||||||
имею т |
одно ит о ж е множ ест в о оп т има льны хт очек. О дн а кот а кка кп р и |
|
||||||||||||||||||||||||||||
п ер еходе от одн огов и да за да чи |
кдр угом ув озм ож н ои зм ен ен и е р а зм ер н ос т и |
|
||||||||||||||||||||||||||||
за да чи (ув ели чен и е чи с ла |
|
п ер ем ен н ы х, ув ели чен и е чи с ла |
огр а н и чен и й), |
т о |
|
|||||||||||||||||||||||||
с ледует |
в ка ж дом |
кон кр ет н ом с луча е а ккур а т н офор м ули р ов а т ь, ка кп он и м а - |
|
|||||||||||||||||||||||||||
ет с я экв и в а лен т н ос т ьда н н ы х за да ч. |
Сфор м ули р уем п р а в и ла , п озв оляющ и е |
|
||||||||||||||||||||||||||||
ос ущ ес т в и т ьэкв и в а лен т н ы е п ер еза п и с и за да ч. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1. |
О бес п ечи т ь н уж н ое н а п р а в лен и е оп т и м и за ци и |
|
целев ой фун кци и |
|
|||||||||||||||||||||||||
в озм ож н ос п ом ощ ью ум н ож ен и я и с ходн ойцелев ойфун кци и н а -1. |
|
|
|
|
||||||||||||||||||||||||||
|
2. Л юбое н ер а в ен с т в ом ож н оум н ож и т ьн а |
-1 и п ер ейт и |
кн ер а в ен с т в у |
|
||||||||||||||||||||||||||
др угогозн а ка . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. О гр а н и чен и е-р а в ен с т в о å |
j =ijbi aм ожx н оза п и с а т ьв |
в и де с и с т ем ы |
|
||||||||||||||||||||||||||
дв ух н ер а в ен с т в |
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
j |
£ijbi a |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
j |
³ijbi .a |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
О т |
огр а н и чен и йн ер а в ен с т в м ож н оп ер ейт и кр а в ен с т в а м , доба в ляя |
|
||||||||||||||||||||||||||
и ли |
от н и м а я н еот р и ца т ельн ы е н ов ы е п ер ем ен н ы е, кот ор ы е в да льн ейш ем |
бу- |
|
|||||||||||||||||||||||||||
дут |
н а зы в а т ьс я доп олнит ельны ми п ер ем ен н ы м и . |
|
Та к, |
|
|
н ер а в ен с т в о |
|
|||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
j |
£ijbi aэквx и в а лен т н о с и с т ем е |
å |
j |
ij |
|
|
, |
|
uii ³ 0b.i +А uн аaлоги= x чн о |
|
|||||||||||||||||||
j=1 |
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
н ер а в ен с т в о å |
j |
³ijbi aэквxи в а лен т н ос и с т ем е |
å |
|
j |
ij |
|
|
, |
uii ³ 0b.i |
- u a= x |
|||||||||||||||||||
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5. О бес п ечи т ьус лов и е н еот р и ца т ельн ос т и |
п ер ем ен н ойм ож н о, и с п оль- |
|
|||||||||||||||||||||||||||
зуя очев и дн ы йфа кт : любое чи с лом ож ет бы т ьп р едс т а в лен ов |
в и де р а зн ос т и |
|
||||||||||||||||||||||||||||
дв ух н еот р и ца т ельн ы х чи с ел: |
= ′ - |
′′ |
′ ³ |
|
x′′ ³ 0,. Есx ли, 0вxxза даx че п р и - |
|
||||||||||||||||||||||||
с ут с т в ов а лот р ебов а н и е x |
|
£ 0, ос ущ ес т в ляет с я за м ен а |
|
|
|
|
′ |
|
|
′ |
³x0. |
|
|
|||||||||||||||||
j |
|
|
|
= - x , x |
j |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
j |
|
|
||||||
|
В |
ка чес т в е |
п р и м ер а |
|
с фор м ули р уем |
фа кт |
экв и в а лен т н ос т и |
дв ух с ле- |
|
|||||||||||||||||||||
дующ и х за да ч ли н ейн огоп р огр а м м и р ов а н и я: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åc j x j |
® min |
|
|
|
|
|
|
|
- åc j x j |
® max |
|
|
|
|
|
|
|
|
|
|
||||||||||
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
j |
£ij i |
, = |
, 1m |
|
(1)i |
|
b a |
x |
|
å |
|
j ij i |
|
|
i |
, |
= |
,+1m |
|
|
(2)=i |
b |
u a x |
||||||
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j ³ |
x= |
|
|
j0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
³ ,i0³ |
=,ux , n1 0, |
|||||||
, n1 |
|
|
|
|
|
j |
|
|
|
|
|
|
i |
|
|
, m1 |
||||||||||||||
11
Л и нейное п р огр а м м и р ов а ни е |
|
|
|
|
|
|
|
|
У т в ер ж ден и е Ес ли |
x * яв ляет с я р еш |
ен и ем |
за да чи |
(1), т он а йдет с я т а - |
||||
кое u* ³ 0, чт о(x* ,u* ) яв ляет с я р еш ен и ем |
|
за да чи (2). С др угойс т ор он ы , ес ли |
||||||
(x€,u€) яв ляет с я р еш ен и ем |
за да чи (2), т о x€ яв ляет с я р еш |
ен и ем за да чи (1). |
||||||
В с в язи с т ем , чт оос н ов н ойм ет од р еш ен и я ЗЛ П |
- с и м п лекс н ы йм ет од |
|||||||
п р едн а зн а чен для р еш ен и я за да ч в |
ка н он и чес койфор м е, м ы п р ои ллюс т р и р у- |
|||||||
ем р а бот уоп и с а н н ы х в ы ш |
е п р а в и л н а |
п р и м ер е п р и в еден и я за да чи кка н он и - |
||||||
чес койфор м е. |
|
|
|
|
|
|
|
|
П р и м ер 1. П ус т ьи с ходн а я за да ча |
за да н а в в и де |
|
|
|||||
|
+ |
-xx |
®xmin |
|
3 |
2 |
||
п р и огр а н и чен и ях |
|
|
1 3 |
|
2 |
|
|
|
|
- + 2x3x1³ 4x2 |
3 |
|
|
||||
|
|
|
|
|||||
-+ - x31 £ 2x2
−x2 − x3 = −20
x2 ³ x3 £ 0 . 0,
Пр и в ес т и да н н ую за да чукка н он и чес койфор м е.
Реш ен и е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. У м н ож и м целев ую фун кци ю н а -1. В р езульт а т е п олучи м |
|
|
|
|||||||||||
|
|
|
- |
- |
|
+xx |
®xmax . |
|
3 |
2 |
|
|
||
|
|
|
|
|
|
1 3 |
|
2 |
|
|
|
|
|
|
2. И |
з лев ойча с т и п ер в огон ер а в ен с т в а в ы чт ем |
н еот р и ца т ельн ую п ер ем ен н ую |
||||||||||||
u1 и п ер ейдем |
когр а н и чен и ям |
|
|
|
|
|
u1 ³ 0 . u1 , 24x3x1 |
x2 |
3 |
|||||
|
|
|
- + |
- = |
|
|||||||||
3. К |
лев ойча с т и в т ор огон ер а в ен с т в а |
|
доба в и м |
н еот р и ца т ельн ую п ер ем ен н ую |
||||||||||
u2 и |
п ер ейдем |
когр а н и чен и ям |
|
|
|
|
|
u2 ³ 03. u2 2, x 1 |
x 2 |
|
||||
|
|
|
- + - + = |
|
|
|||||||||
4. У м н ож и м обе ча с т и |
т р ет ьегор а в ен с т в а |
н а |
-1 |
|
|
|
|
|
||||||
|
|
|
|
x2 + x3 = 20. |
|
|
|
|
|
|
||||
5. О с ущ ес т в и м |
за м ен уп ер ем ен н ы х |
1 |
' |
|
'' |
|
' |
x'' |
³ x. 0,xx |
³ x, 0= - |
||||
|
|
|
|
|
1 |
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
= - |
¢ , |
xx' |
³ 0x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
В р езульт а т е за да ча п р и н и м а ет ка н он и чес ки йв и д |
|
|
|
|
|
|||||||||
|
|
|
' |
'' |
|
|
x |
' |
|
|
- |
+ |
23 |
3 |
|
|
|
1 |
1 |
|
2 |
3 ®xmax- x |
|||||||
|
|
|
' |
'' |
|
|
|
' |
u1 = x4 |
- xx -- 3x - 2 |
2 |
|||
|
|
|
1 |
1 |
|
2 |
|
3 |
||||||
|
|
|
' |
'' |
|
|
' |
u2 =x2 +x +x +- + |
|
|||||
|
|
|
1 |
1 |
2 |
3 |
|
|||||||
|
|
|
|
x2 - x3' = 20 |
|
|
|
|
|
|
|
|||
|
|
' |
'' |
|
|
' |
|
u1 |
u2 ³ 0. |
³, 0 x ³, 0 x ³, 0 x ³, 0 |
||||
|
|
1 |
1 |
2 |
|
3 |
|
|||||||
За м ет и м , чт оп ос ледов а т ельн ос т ьп р и м ен ен и я п р а в и л п р и в еден и я кка н он и - чес койфор м е н е с ущ ес т в ен н а и м ож ет бы т ьлюбой.
12
