Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лин. програм. учеб. пособие (Азарнова Т. В

.).pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

538.99 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Л и нейн ое п р огр а м м и р ов а ни е

2. На

за ключи т ельн ойи т ер а ци и , кр ом е т ого, когда п олучен а оп т и м а ль-

н а я т очка, оцен ки в с ех в ект ор ов Aj

н еот р и ца т ельн ы

−1

==, 1n ³j0, -

Ac B

и ли

−1

T T =³ c, T y =A A y Ac B

−1

т .е. в ект ор

ByB

c яв ляет с я доп ус т и м ы м в дв ойс т в ен н ойза да че, кр ом е т о-

го, он яв ляет с я р еш

ен и ем дв ойс т в ен н ойза да чи .

П р и

эт ом

за м ет и м , чт оча с т ь

огр а н и чен и й

дв ойс т в ен н ой

за да чи

в ы п олн яет с я

в и де

р а в ен с т в

( T )j =

j ,

Î I ,

гдеj cI -Aм нyож ес т в оба зи с н ы х и н декс ов

(т а кка коцен ки ба -

зи с н ы х в ект ор ов в с егда

р а в н ы

н улю

= 0, j Î I ). Та ки е т очки y н а зы в а ют -

с я ба зи с н ы м и

дв ойс т в ен н ойза да че.

Ра с с м от р и м

п р и м ер ы п р и м ен ен и я и злож ен н ойт еор и и

дв ойс т в ен н ос т и

кр еш ен и ю за да ч ли н ейн огоп р огр а м м и р ов а н и я.

П р и м ер

3. На

ос н ов а н и и гр а фи чес кого а н а ли за

дв ойс т в ен н ойза да чи

и с с ледов а т ьр а зр еш

и м ос т ьс ледующ и х за да ч и

с луча е р а зр еш и м ос т и н а йт и

оп т и м а льн ое зн а чен и е целев ойфун кци и .

а )

® minx

б)9

x x® minx2

3 1

- + 2 +xx

³ 3x

- + + x = 2x

1 3

3 + - x31 ³1x2

- xx31 =31 x2

³ x31 ³ 0 x2 , 0

Реш ен и е.

Дв ойс т в ен н ы е кп р едлож ен н ы м

за да ча м

от н ос ят с я кза да ча м

ли н ейн о-

го п р огр а м м и р ов а н и я в

R2 и

п оэт ом у

и х м ож н о р еш а т ь оп и с а н н ы м в

§1

гр а фи чес ки м

м ет одом .

Дв ойс т в ен н а я кза да че а ) и м еет

в и д:

3y1 + y2 ® max

- y1 + 3y2 £ 6

2y1 + y2 £ 9 y1 - y2 £ 3 y1, y2≥0

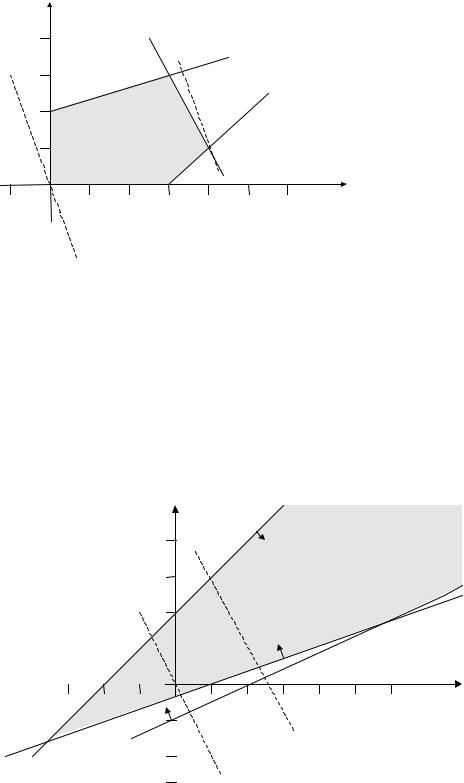
Л и нейное п р огр а м м и р ов а ни е

					2
					1
			Y		d=12	3
					.Y* max
					Y1
					Y1
			d=0
					Ри с .6			= ( 41,) с
Г р а фи чес кое р еш ен и е да н н ойза да чи (Ри с . 6) п ока зы в а ет , чт оY *								= ( 41,) с
							max
zmax*	= 13.		В с и луп ер в ойт еор ем ы дв ойс т в ен н ос т и				и с ходн а я за да ча	т а кж е
и м еет р еш		ен и е, п р и чем		оп т и м а льн ое зн а чен и е р а в н о13.
	Дв ойс т в ен н а я за да ча				кза да че б) и м еет в и д:
					2y1 + y2 → max
					− y1 + y2 ≤ 2
					y1 − 3y2	≤ 1
					y1 − 2y2	≤ 2
					Y
						Y1
		2		3	d=0	d=5
		2	1		d=0	d=5
			1
					Ри с .7
					34

Л и нейн ое п р огр а м м и р ов а ни е

Г р а фи чес ки йа н а ли з п ока зы в а ет , чт одв ойс т в ен н а я за да ча н ер а зр еш и м а и з-за н еогр а н и чен н ос т и целев ойфун кци и , п оэт ом у п о с в ойс т в у 3 и с ходн а я


за да ча н ер а зр еш и м а и з-за п ус т от ы доп ус т и м огом н ож ес т в а .
П р и м ер 4. О п р едели т ь, яв ляют с я ли да н н ы е в ект ор ы								x и y	оп т и м а ль-
н ы м и р еш ен и ям и да н н ойза да чи и дв ойс т в ен н ойкн ей:
+	+ xx	® maxx						8	10
	1 3			2
+ 4	+xx		= 2x	2
	1 3			2
+ 2	−xx		= 0x	2
	1 3			2
³	³ x31 ³ 0 x2 , 0							0,
			æ 9			7	ö
x (	), 1,1y0,= ç				,-		÷ =
x (	), 1,1y0,= ç				,-	2	÷ =
			è 2			2	ø

	Реш ен и е. Реш ен и е да н н ойза да чи ос ущ ес т в ляет с я в н ес колькоэт а п ов :
1)	п одс т а в и м	т очку x = (	1,)10,в		огр а н и чен и я и с ходн ойза да чи ; т а кка кт очка
	удов лет в ор яет огр а н и чен и ям , п ер еходи м					кс ледующ ем уэт а п у;
2)	п ос т р ои м	дв ойс т в ен н ую за да чу
					2y1 ® min
					y1 + y2 ³ 1
					y1 +	y2 ³ 104	2
					y1 - y2 ³ 8 ;
		æ 9		7	ö
3)	п одс т а в и м	т очку y = ç	,-		÷ в огр а н и чен и я дв ойс т в ен н ойза да чи ; т очка
3)	п одс т а в и м	т очку y = ç	,-	2	÷ в огр а н и чен и я дв ойс т в ен н ойза да чи ; т очка
		è 2		2	ø

удов лет в ор яет огр а н и чен и ям , п ер еходи м кс ледующ ем уэт а п у;

4) п одс т а в и м			т очку x = ( 1,)10,в целев ую фун кци ю и с ходн ойза да чи , а т очку
æ 9		7	ö
y = ç	,-		÷ - в целев ую фун кци ю дв ойс т в ен н ойза да чи ; п олучен н ы е зн а -
		2
è 2			ø

чен и я с ов п а да ют , п оэт ом уп ос в ойс т в у4 да н н ы е т очки яв ляют с я с оот в ет -

с т в ен н ор еш ен и ем и с ходн ойи	дв ойс т в ен н ы х за да ч.
П р и м ер 5. На йт и р еш ен и е с ледующ ейЗЛ П									п ут ем			гр а фи чес когоа н а -
ли за дв ойс т в ен н ойза да чи :				+ x		®xmaxx
5	+	+		+ x	4	®xmaxx				2
					4			31		2
	4	+		x + x		4	= 16x
				1		4			3
		-	-	+ x			4	=xx4			x	2	6	4
							4		1 3			2
	³	³		3 ³ x4 ³ 0 .x1 , 0 x2 , 0 0,
		Реш ен и е.
Дв ойс т в ен н а я за да ча за п и ш		ет с я в		в и де
		y1 +	y2 ® min										4	16
		y1 +		y2 ³ 54					6
		- 4y2 ³ 1

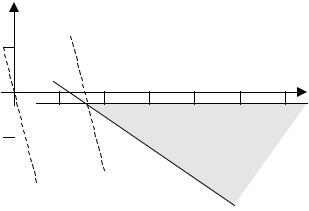
Л и нейное п р огр а м м и р ов а ни е

y1 - y2 ³ 1 y1 + y2 ³ 1

y1, y2≥0

Г р а фи чес ки йа н а ли з эт ойза да чи п ока за н н а с ледующ ем р и с ун ке.

Y2
.	Y1
.
Y*min
	d=9
d=0
	Ри с . 8

Y *

1 ö

О п т и м а льн ы м р еш ен и ем

яв ляет с я в ект ор

= ç

÷ ,

= 25. На ос -

min

è 8

4 ø

min

н ов а н и и

в т ор ойт еор ем ы дв ойс т в ен н ос т и

для в ект ор а x*,яв ляющ егос я р еш е-

н и ем

и с ходн ойза да чи долж н ы , в ы п олн ят ьс я р а в ен с т в а

y*x +y= 0 -) 5

y*x( y-= 0 -)1

- = 0 -)1 ( 4

y*x( y+= 0 .-)1

П одс т а в ляя коор ди н а т ы в ект ор а Ymin* , п олуча ем , чт о п ер ем ен н ы е x3 и x4 и с ходн ойза да чи долж н ы обр а щ а т ьс я в н уль. Тогда и з и с ходн ойс и с т ем ы п о-

луча ем

4x1 = 16, от куда

x1 = 4,

x1 − x2 = 46, от куда4

x2 = 5. Следов а т ель-

н о,

р еш ен и ем и с ходн ойза да чи

яв ляет с я в ект ор X max*

) 0,. П0,р5,и(4эт ом

zmax*

+ 5=254*.

П р и м ер 6. О п р едели т ь р еш ен и е

дв ойс т в ен н ойза да чи кза да че и з п р и -

м ер а 1 § 4, и с п ользуя р еш ен и е и с ходн ойза да чи .

Реш ен и е.

В с оот в ет с т в и и с

за м еча н и ем

1 оп т и м а льн ы м р еш

ен и ем дв ойс т в ен н ой

æ1

æ3

за да чи

яв ляет с я в ект ор

= TyB−1c = (

, где м а т р и ца B−1

1,)2,30

0 1

è1

Л и нейн ое п р огр а м м и р ов а ни е

яв ляет с я	м а т р и цей		обр а т н ой к оп т и м а льн ой ба зи с н ой м а т р и це
		æ -	1 0	ö	1
= [		ç	0	÷	. 1
= [	AB A]=A		0	÷	. 1
	53 1	ç		÷
		ç	10	÷	1
		è	10	ø	1

				Задачи длясам о ст о ят ельн о го реш ен ия
1. Сос т а в и т ьдв ойс т в ен н ы е за да чи															кс ледующ и м				и с ходн ы м			и п р ов ер и т ь
с в ойс т в о1 дв ойс т в ен н ы х										за да ч:
1)	-	+	- x			4		®xmax x					2		2		3
						4			13				2
	- +		- x4 £ 52x3x1 3 x2												2		3)		-	+	-		+ x				®xmin2						x	x			3
	+ 2 - + x							£x3x			x						3)		-	+	-		+ x		5		®xmin2						x	x	2		3
	+ 2 - + x					4		£x3x			x	2													5					4			31		2
						4			1 3			2							- + -					- x				2= 10x					x	x 3
	³		³			³ x4 ³ 0 ;x31									, 0 x2		, 0	0,	- + -					- x				2= 10x					x	x 3
																										5				4			31		2
																			+	- +				+ x						³28x			xx		2x
2)			3x3 - x4					® max											+	- +				+ x					5	³28x		4	xx		2x	2
																													5			4	1 3			2
																			- +			- + x5 £ 4 x4 2x3x1													x2
	- 2		+ x4 = x81									x2							- +			- + x5 £ 4 x4 2x3x1													x2
	- 2		+ x4 = x81									x2							³		³ x41 ³ 0.x3 , 0												0,
		+ - 3xx = 6x									3								³		³ x41 ³ 0.x3 , 0												0,
							4 2				3
³		³	³ x4 ³ 0 x31 , 0 x2 , 0														0,
2. На ос н ов а н и и гр а фи чес когоа н а ли за																дв ойс т в ен н ойза да чи и с с ледов а т ьр а з-
р еш	и м ос т ь с ледующ и х за да ч												и в		с луча е р а зр еш				и м ос т и н а йт и оп т и м а льн ое
зн а чен и е целев ойфун кци и :
1)	-	+	- x					4	® maxx x					x 2		2	4		+ 3	+xx		£ -x2
								4			3 1			2							1 3		2
	- +			- x4 £ 52x3x1									x2		2				-	+ x31 ³41 x2 4
	-		+		- x4 ³ x431								2x2		2		x1 ³ x2 ³ 0;						0,
																	4)		+	+	x x® minx2										2
2)	-	+	-		x			® minx x					2x		6						3 1		2
2)	-	+	-		x		4	® minx x					2x	2	6		- + + x31 = 2x2
							4		3 1					2			- + + x31 = 2x2
		+ 2x1 - x4 = x43																	-	- xx =31 x				2		2
	- + - 3x4 ³ 8x31										x2										31			2
	- + - 3x4 ³ 8x31										x2								³	³ x ³ 0. x , 0													0,
	³		£ x41 ³ 0;x3								, 0			0,								31				2
	³		£ x41 ³ 0;x3								, 0			0,
3)	-		+ xx		® minx										4 3		12
			13						2
3. Для ка ж дойи з п а р ы									дв ойс т в ен н ы х за да ч в озм ож н ы												т р и в а р и а н т а									от в ет а :
за да ча р а зр еш и м а					(Р),				фун кци я н е огр а н и чен а									(Н),		обла с т ь п ус т а я (П ). Эт о
п озв оляет , в ообщ е гов ор я, р а с с м от р ет ь9 с и т уа ци й: РР (обе за да чи																										р а зр еш и -
м ы ), РН(п ер в а я р а зр еш и м а , в ов т ор ойцелев а я фун кци я н е огр а н и чен а ) и																															т .д.
У ка за т ьв с е в озм ож н ы е с и т уа ци и .
4. П р и в ес т и п р и м ер ы								дв ойс т в ен н ы х п а р , обла да ющ и х с ледующ и м и																					с в ойс т -
в а м	и .
1)	обе за да чи		и м еют оп т и м а льн ы е р еш ен и я;
2)	одн а	за да ча и м еет						н еогр а н и чен н ую доп ус т и м ую обла с т ь, в т ор а я - п ус т ую

обла с т ь;

Л и нейное п р огр а м м и р ов а ни е

3)доп ус т и м ы е обла с т и обеи х за да ч п ус т ы е;

4)доп ус т и м ы е обла с т и обеи х за да ч н еогр а н и чен н ы е.

5. О п р едели т ь, яв ляют с я ли да н н ы е в ект ор ы x и y р еш ен и ям и да н н ойза да - чи и дв ойс т в ен н ойкн ей:

+ 4	+xx	®xmax
	1 3		2
+	+ xx		= 9 x	2	2 5	12
		13		2

+ xx

= 11x

4 3

³ x31 ³ 0 x2 , 0

1 ö

x = (

), 2,y10,= ç

÷.

14 ø

Реш и т ь дв ойс т в ен н ы е за да чи , и с п ользуя р еш

ен и е и с ходн ы х за да ч

с и м -

п лекс н ы м

м ет одом :

xx ® maxx

+ + x

®xminx

+xx

³ 5x

- - 2 + x

£ 6x x

1 3

3 1

+ + 2x3x1³ 10x2

- x1

+ x3

£ 2

- + 3 -xx

³ 2x

+ 2x

£ 8x

1 3

³ x31 ³ 0 x2 , 0

³ x4 ³ 0 x31 , 0 x2 , 0

+ x

®xmaxx

x 2

3 1

=x210

3 1

+ x1 + x4 = 7x3

+ x1 + x5 = 4x33

³ x5 ³ 0 x4 , 0 x31 , 0 x2 , 0

7. Тран сп о рт н аязадача

Тр а н с п ор т н а я за да ча

фор м ули р ует с я с ледующ и м

обр а зом . И

м еет с я m

п ун кт ов п р ои зв одс т в а

A1, A2,..., Am одн ор одн огоп р одукт а

n п ун кт ов п о-

т р еблен и я

B1, B2,..., Bn . За да н ы объем ы п р ои зв одс т в а

ai ,

i =

ка ж дого

1, m

п ун кт а Ai

и р а зм ер ы с п р ос а ка ж дого п ун кт а

bj ,

j =

одн и х и т ех ж е

1, n

еди н и ца х и зм ер ен и я . И

зв ес т н а

т а кж е м а т р и ца

= =

р а ,с=j- , 1m

( i C),

, 1n

ходов cij ,

с в яза н н ы х с п ер ев озкойеди н и цы п р одукци и

и з п ун кт а

Ai в п ун кт

B j . Тр ебует с я с ос т а в и т ьп ла н п ер ев озок, обес п ечи в а ющ и йп р и м и н и м а льн ы х

с ум м а р н ы х р а с хода х

удов лет в ор ен и е в с ех п ун кт ов

п от р еблен и я

за

с чет

и м еющ егос я в

п ун кт а х п р ои зв одс т в а

п р одукт а .

П р и в еден н а я фор м ули р ов ка п р едп ола га ет

н а ли чи е р а в ен с т в а

(ус лов и я

ба ла н с а )

Л и нейн ое п р огр а м м и р ов а ни е

å ai = å bj .

i=1

j=1

Та ка я за да ча

н а зы в а ет с я за кр ы т ойт р а н с п ор т н ойза да чей. М а т ем а т и че-

с ка я п ос т а н ов ка эт ойза да чи

и м еет

с ледующ и йв и д

å å

(1)

® min

п р и огр а н и чен и ях

i=1 j=1

å x ij

= ai

i =

(2)

1, m

j=1

å x ij = bj

j =

1, n

(3)

i=1

x ij

³ 0

(4)

i = 1 m

j = 1 n

где x ij - коли чес т в оп р одукт а , п ер ев ози м ое и з п ун кт а

Ai в

п ун кт B j .

Без огр а н и чен и я общ н ос т и в с егда

и,

м ож н ос чи т а т ь, чт о ai > 0 i = 1 m

j >

. 0,j

, 1n

За да ча (1)-(4) яв ляет с я за да чейли н ейн огоп р огр а м м и р ов а н и я, за п и с а н -

н ойв ка н он и чес койфор м е. О н а и м еет

mn п ер ем ен н ы х и m + n огр а н и чен и й.

юба я доп ус т и м а я т очка за да чи

м ож ет бы т ьза п и с а н а

в и де м а т р и цы

æ x

...

x1n

X = (x ij ) =

...

ç ...

÷ .

...

èx m1

x mn ø

К а ки зв ес т н о, н е люба я за да ча ли н ейн огоп р огр а м м и р ов а н и я и м еет

р е-

ен и е. У с лов и я р а зр еш и м ос т и

т р а н с п ор т н ойза да чи

фор м ули р уют с я в

с ле-

дующ ейт еор ем е.

Тео рем а 1.

Для р а зр ешимост и т р а нсп ор т ной за да чи необходимо и

дост

а т очно вы п олнение следую щ его условия ба ла нса

å ai

å bj .

i=1

j=1

М ож н о п ока за т ь, чт о чи с ло н еза в и с и м ы х ур а в н ен и й с и с т ем ы

(2)-(3)

р а в н о m + n − 1. О т с юда , в ча с т н ос т и ,

с ледует , чт олюба я доп ус т и м а я ба зи с -

н а я т очка т р а н с п ор т н ойза да чи

с одер ж и т

н е более m + n − 1 п олож и т ельн ы х

коор ди н а т .

Ра с с м от р и м

дв а м ет ода

н а хож ден и я

и с ходн ой ба зи с н ой т очки

для

т р а н с п ор т н ойза да чи : м ет од "с ев ер о-за п а дн огоугла " и

м ет од м и н и м а льн ого

элем ен т а .

и нейное п р огр а м м и р ов а ни е

М ет о д "сев еро -зап адн о го угла"

А лгор и т м

п ос т р оен и я и с ходн ойба зи с н ойт очки с кла ды в а ет с я и з н ес кольки х

а гов , н а

ка ж дом

и з кот ор ы х оп р еделяет с я в ер хн и йлев ы йэлем ен т

м а т р и цы

X . Сфор м ули р уем

а лгор и т м

м ет ода "с ев ер о-за п а дн огоугла ".

а г 0. П ола га ем

′

== , n1.

,=j

, m1

а г 1. П ола га ем

(

i′ ,b′j

)a. Есminли xi

= ai′

, т оп ер еходи м

кш а гу2,

п р от и в н ом с луча е - кш а гу4.

а г 2. П ола га ем

′j0 =

′j0

− xbi0 j0 . bИ

н декс у i0

п р и с в а и в а ем

зн а чен и е

+ 1.

Ес ли

= m , т оп ер еходи м

кш а гу3, в

п р от и в н ом

с луча е кш а гу1.

а г 3. П ола га ем

= b′

для в с ех

j ³ j

. Реш ен и е за кон чен о.

i′0

а г 4. П ола га ем

− xai0 j0 . Иa н декс у j0

п р и с в а и в а ем

зн а чен и е

+ 1.

Ес ли

= n , т оп ер еходи м

кш а гу5, в п р от и в н ом

с луча е п ер еходи м

кш а гу1.

а г 5. П ола га ем

x 0

= ai′

дляijв с ех i ³ i0 . Реш ен и е за кон чен о.

Ра с с м от р и м

п р и м ер

и с п ользов а н и я да н н огоа лгор и т м а .

П р и м ер 1. И с ходн ы е да н н ы е:

b j

в ер хн ем

п р а в ом

углу

ка ж дой

ячейке

с т оят

коэффи ци ен т ы

j = c5,.1Даi ,н,н4,а 1я за да ча яв ляет с я за кр ы т ойт р а н с п ор т н ойза да чей, т а к

ка кс ум м а

п от р ебн ос т ейв

п р одукт е р а в н а

с ум м е и м еющ егос я п р одукт а

45+70+15+50=30+36+36+22+56.

Результ а т ы р а бот ы

а лгор и т м а за п и с а н ы в

в н и ж н ем

лев ом углуячейки .

П о-

лучен а и с ходн а я ба зи с н а я т очка

			Л и нейн ое п р огр а м м и р ов а ни е
æ	0 0 ö			0	15	30
ç	0	÷	13		36 0	21
ç	0	÷	13		36 0	21
X = ç	06	÷	09	0
ç	06	÷	09	0
ç		÷	0	0
è	500ø		0	0

с o зн а чен и ем	целев ойфун кци и р а в н ы м	804.
М ет од	"с ев ер о-за п а дн ого угла "	м ож ет ока за т ьс я очен ь "да леки м " от
оп т и м а льн ого, т а кка кп р и п ос т р оен и и		н а ча льн ойба зи с н ойт очки эт и м м ет о-
дом м ы с ов с ем н е р еа ги р уем н а коэффи ци ен т ы целев ойфун кци и cij . Ва ж н о
и м ет ь п р ос т ойм ет од, п озв оляющ и йс т р ои т ь н а ча льн ую ба зи с н ую т очку в о
м н оги х с луча ях бли зкую коп т и м а льн ой. Та ки м м ет одом яв ляет с я н екот ор а я
м оди фи ка ци я м ет ода "с ев ер о-за п а дн огоугла " - м ет од м и н и м а льн огоэлем ен -

т а .

Алго рит м

м ет о да м ин им альн о го элем ен т а

а г

0. П ола га ем

¢ = ,

j)Îi,Ω( , bгдеa Ωb

}. ,=j , m1 :ii)(

i j

, n1

а г

1. О п р еделяем

п а р уи н декс ов

(i0 , j0 ) и з ус лов и я

min c = c 0 j0 i.

x ( i¢ ,b¢j

)a. Есminли xi

i j)( ,Ω

а г 2.

П ола га ем

= ai¢

, т оп ер еходи м

кш а гу

3, в п р от и в н ом

с луча е - кш

а гу6.

а г

3. П ола га ем

¢j0

- xbi0 j0 . b

Ш а г 4. Ω = Ω {( 0

)

}. \ :ji

, n1

а г 5. Ес ли

м н ож ес т в о Ω с ос т ои т

и з элем ен т ов

одн ойс т р оки ik , т оп ола га -

ем

= b¢

для в с ех

j) Ω .

Реш ен и е за кон чен о. В п р от и в н ом

с луча е

п ер еходи м кш а гу1.

а г 6. П ола га ем

i¢0

- xai0 j0 . a

Ш а г 7. Ω = Ω {(

0 ) :=

}. i\ i ,j

, 1m

а г 8. Ес ли

м н ож ес т в о Ω с ос т ои т

и з элем ен т ов одн огос т олбца jk , т оп о-

ла га ем

x k = ai¢

дляij в с ех (i, jk ) Ω . Реш ен и е за кон чен о. В п р от и в н ом с лу-

ча е п ер еходи м кш а гу1.

Да н н ы м

м ет одом н а йдем

и с ходн ую ба зи с н ую т очкудля п р и м ер а 1.

Л и нейное п р огр а м м и р ов а ни е
П р и м ер		2.
	b j	30	36		36	22			56
ai		30	36		36	22			56
ai		3		4	2		4		5
45		3		4	2		4		5
45					36(2)			9(5)
					36(2)			9(5)
70		3		1	4		2		4
70		36(1)			22(3)			12(5)
		36(1)			22(3)			12(5)
15		4		3	5		3		6
15								15(5)
50		2		4	3		6		8
50	30(4)							20(5)
Для н а глядн ос т и ка ж ды йэлем ен т с н а бж ен и н декс ом , р а в н ы м								н ом ер уи т ер а -
ци и , н а	кот ор ойбы л п олучен			да н н ы йэлем ен т . В р езульт а т е п олучи ли						с ле-
дующ ую ба зи с н ую т очку
			æ		9 ö	0	360	0
			ç		÷	22	00		36
			ç		12÷	22	00		36
		X = ç			÷	0	0	0
			ç		150	0	0	0
			ç		÷
			ç		÷	0		0	30
			è		200ø	0		0	30
с озн а чен и ем		целев ойфун кци и , р а в н ы м 545. Да н н ое зн а чен и е яв н ом ен ьш е,
чем зн а чен и е целев ойфун кци и				н а ба зи с н ойт очке, п олучен н ойм ет одом						"с е-
в ер о-за п а дн огоугла ".
Зам ечан ие 1. П р и зн а ком				в ы р ож ден н ос т и т р а н с п ор т н ойза да чи яв ляет -
с я с ущ ес т в ов а н и е r < m,			s < n , для кот ор ы х в ы п олн яет с я р а в ен с т в о
				r	s
				å aik	= åbjl .
				k =1	l=1
В эт ом	с луча е п р и и с п ользов а н и и п р и в еден н ы х а лгор и т м ов м ож ет ока за т ьс я,
чт ос р еди n + m − 1 ба зи с н ы х коор ди н а т ес т ьн улев ы е.
П р и м ер		3. П ос т р ои м	м ет одом		"с ев ер о-за п а дн ого угла " и с ходн ую ба -
зи с н ую т очкудля с ледующ ейза да чи
				42

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.05.201539.94 Кб63Лекция. Обработка звучащей речи.doc
#
20.05.2015337.55 Кб7Ленина.rtf
#
17.07.20191.4 Mб76лесомелиорация курск. кулешова.docx
#
19.03.2016142.85 Кб27ЛетописьПознания.doc
#
22.08.201938.25 Кб2лизации расплавленного базальта.docx
#
21.05.2015538.99 Кб15Лин. програм. учеб. пособие (Азарнова Т. В.).pdf
#
20.05.201546.59 Кб9ЛИннгв идеи эпохи возрождения (2).doc
#
21.05.20151.38 Mб78Линтер методичка.pdf
#
19.03.201693.18 Кб1Липинский Д.А. Проблемы совершен. проц. отв..doc
#
21.05.2015210.4 Кб15литература 17-18вв.pdf
#
19.03.2016501.25 Кб219литература 18 века 1.doc