
Лабораторные работы по ТВиМС
.pdf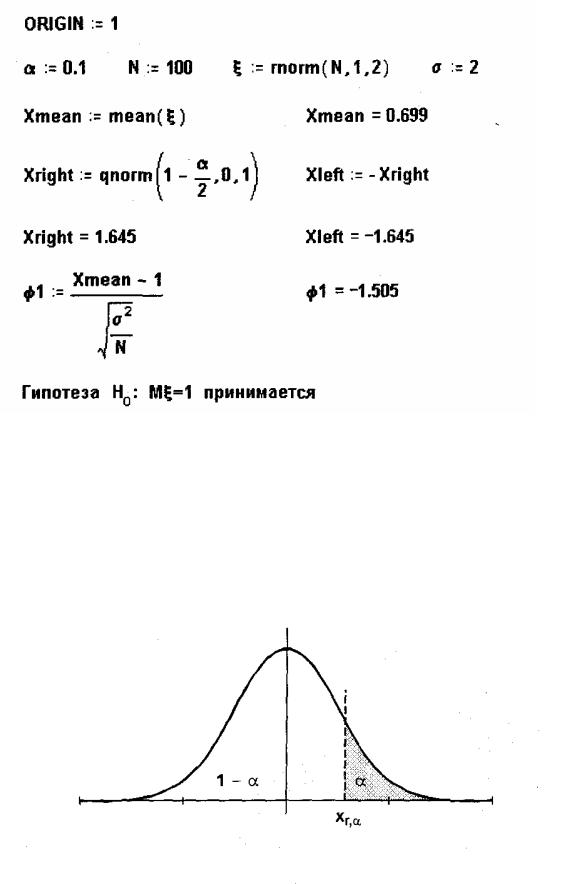
31
Ука за ние. Снач ала с п омощ ью функ ци и rnorm(N,m,σ) сг е не ри рована
вы борк а |
объ е ма N = |
100 и з знач е ни й |
случ ай ной |
ве ли ч и ны , |
и ме ющ е й |
|||
нормальное расп ре де ле ни е N(1,2). Для уровня знач и мости |
α=0.1 |
вы ч и сле ны |
||||||
г рани цы |
к ри ти ч е ск ой |
области , Xright = 1.645, Xleft |
= |
-1.645, |
и |
оце нк а |
||
мате мати ч е ск ог о ож и дани я Х mean = 1.12. В ы ск азана нулева я гипо т еза |
о т о м, |
|||||||
ч т о знач е ни е п араме тра М ξ =a равно а0 = 1, т.е . Н0: a0 |
= 1. З ате м вы ч и сле но |
|||||||
знач е ни е |
к ри те ри я ϕ = |
-1.505 |
и , п оск ольк у -1.505 (-1.645,1.645), |
нуле вая |
||||
г и п оте за п ри ни мае тсяна уровне |
знач и мости |
α =0.1. |
|
|
|
|
||
В рассматри вае мом случ ае |
к ри ти ч е ск ая область знач е ни и к ри те ри я ϕ, п ри |
|||||||
к оторы хг и п оте за H0 отве рг ае тся, п равосторонняя(ри с. 3). |
|
|
|
|||||
Ри с. 3. К ри ти ч е ск аяобластьдляальте рнати вной г и п оте зы H1: a>a0

|
|
|
32 |
|
|
|
К ри ти ч е ск ая точ к а удовле творяе т услови ю |
P(ϕ > xr,α ) = α и находи тсяк ак |
|||||
ре ше ни е уравне ни я ϕ(xr,α ) = 1− α . |
|
|
|
|
||
К ог да |
к ри ти ч е ск ая |
область |
най де на, мож но |
вы ч и сли ть п о |
вы борк е |
|
знач е ни е к |
ри те ри я ϕ и |
п рове ри ть, |
п оп адае т ли |
оно |
в к ри ти ч е ск ую |
область. |
Е сли ϕ > xr ,α , то ги п оте за H0 отве рг ае тся и п ри ни мае тся г и п оте за H1. Е сли ж е ϕ < xr,α , то г и п оте за H0 не отве рг ае тся.
Ни ж е |
п ри ве де |
н фраг ме нт |
рабоч е г о док уме нта Mathcad, |
соде рж ащ и й |
||
п рове рк у |
г и п оте зы |
H0: a |
= a1 |
о |
ве ли ч и не мате мати ч е ск ог о |
ож и дани я а |
нормально |
расп ре де ле нной |
случ ай ной |
ве ли ч и ны п ри альте рнати вной ги п оте зе |
|||
H1: a > a1.
В |
тре тье м случ ае |
с |
нуле вой |
г и п оте зой |
H0: a = a1 |
и |
альте рнати вной |
|||||||
г и п оте зой |
H1: a < a1 |
оп ять задади мся не к оторы м уровне м знач и мости α и |
||||||||||||
вы ч и сли м п о вы борк е |
x = (x1, x2 ,.., xn ) знач е ни е |
к ри те ри яϕ = |
x |
− a0 |
, |
|
||||||||
|
|
|
|
|||||||||||
σ 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x = 1 n |
|
|
|
|
|
|
|
n |
|
|||
г де |
x . |
|
|
|
|
|
|
|
|
|
|
|||
|
|
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n åi=1 |
|
|
|
|
|
|
к ри те ри я ϕ п ри |
||||
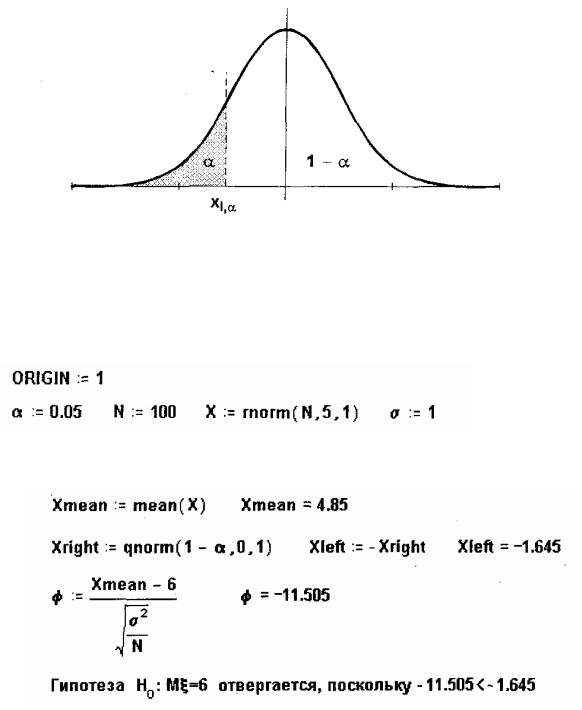
В |
рассматри вае мом случ ае к ри ти ч е ск ая область знач е ни и |
|||||||||||||
к оторы хг и п оте за H0 отве рг ае тся, ле восторонняя(ри с. 4). |
|
|
|
|
|
|
||||||||
К ри ти ч е ск ая точ к а удовле творяе т услови ю P(ϕ < xl,α ) = α |
и находи тся п о |
|||||||||||||
формуле |
xl,α |
= − xr ,α , |
г де |
xr,α – |
ре ше ни е |
уравне ни я Φ(xr,α ) = 1− α . К ог да |
||||||||
к ри ти ч е ск аяобластьнай де на, мож но вы ч и сли тьп о вы борк е |
знач е ни е |
к ри те ри я |
||||||||||||
ϕ и |
п рове ри ть, п оп адае т |
ли |
оно |
в к ри ти ч е ск ую область. |
|
Е сли ϕ < xl,α , то |
||||||||
г и п оте за |
H0 |
отве рг ае тся |
и |
п ри ни мае тся г и п оте за H1. Е сли |
ж е |
ϕ > xl,α ,то |
||||||||
г и п оте за H0 не |
отве рг ае тся. |
|
|
|
|
|
|
|
|
|
|
|||
33
Ри с. 4. К ри ти ч е ск аяобластьдляальте рнати вной г и п оте зы H1:a<a0
Ни ж е |
п ри ве де н |
фраг ме нт |
рабоч е г о док уме нта Mathcad, |
соде рж ащ и й |
|
п рове рк у |
г и п оте зы |
о ве ли ч и не |
мате мати ч е ск ог о |
ож и дани я а |
нормально |
расп ре де ле нной случ ай ной ве ли ч и ны H0: a = 6 п ри |
альте рнати вной г и п оте зе |
||||
H1: a < 6. |
|
|
|
|
|
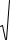
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
||
|
З АДАН И Е 7 а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Смоде ли руй те |
вы борк у |
100 |
|
|
знач е ни й |
нормально |
расп ре де ле нной |
||||||||||||||||||||||
случ ай ной |
ве ли ч и ны |
с |
ук азанны ми |
|
п араме трами . |
Сформули руй те |
нуле вую |
|||||||||||||||||||||||
г и п оте зу о |
ве ли ч и не |
мате мати ч е ск ог о |
ож и дани я и |
п рове рьте |
для заданны х |
|||||||||||||||||||||||||
уровне й |
знач и мости |
три альте рнати вны е |
ги п оте зы . |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
П ор я д ок вы полнени я зад ани я |
|
|
|
|
|
||||||||||||||||||
1. |
Смоде ли руй те оп и санную в услови и вы борк у. |
|
|
|
|
|
|
|||||||||||||||||||||||
2. |
Най ди те п о вы борк е |
точ е ч ную оце нк у мате мати ч е ск ог о ож и дани я. |
|
|||||||||||||||||||||||||||
3. |
Сформули руй те |
нуле вую |
г и п оте зу о знач е ни и мате мати ч е ск ог о ож и дани я |
|||||||||||||||||||||||||||
4. |
H0: a = a0. |
знач е ни е |
к ри те ри я. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
В ы ч и сли те |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5. |
Най ди те |
г рани цы |
|
к ри ти ч е ск ой |
|
области |
для |
альте рнати вной |
ги п оте зы |
|||||||||||||||||||||
|
H1: a ¹ a0. |
|
знач е ни е |
|
к ри те ри я |
с |
г рани цами |
к ри ти ч е ск ой |
области |
и |
||||||||||||||||||||
6. Сравни те |
|
|
||||||||||||||||||||||||||||
|
сформули руй те |
соотве тствую щ е е |
|
утве рж де ни е . |
|
|
|
|
|
|
||||||||||||||||||||
7. |
Най ди те |
г рани цы |
|
к ри ти ч е ск ой |
|
области |
для |
альте рнати вной |
ги п оте зы |
|||||||||||||||||||||
8. |
H1: a > a0. |
знач е ни е |
|
к ри те ри я |
с |
г рани цами |
к ри ти ч е ск ой |
области |
и |
|||||||||||||||||||||
Сравни те |
|
|
||||||||||||||||||||||||||||
|
сформули руй те |
соотве тствую щ е е |
|
утве рж де ни е . |
|
|
|
|
|
|
||||||||||||||||||||
9. |
Най ди те |
г рани цы |
|
к ри ти ч е ск ой |
|
области |
для |
альте рнати вной |
ги п оте зы |
|||||||||||||||||||||
|
H1: a < a0. |
знач е ни е |
к ри те ри я |
|
с |
|
г рани цами |
к ри ти ч е ск ой |
области |
и |
||||||||||||||||||||
10. Сравни те |
|
|
|
|||||||||||||||||||||||||||
|
сформули руй те |
соотве тствую щ е е |
|
утве рж де ни е . |
|
|
|
|
|
|
||||||||||||||||||||
|
П р и мер вы полнени я |
зад ани я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
В |
к аж дом |
и зп ри ве де нны х вы ше |
тре х фраг ме нтов рабоч и х док уме нтов |
||||||||||||||||||||||||||
Mathcad п рове де ны п рове рк и дляодной |
и зальте рнати вны хги п оте з. |
|
|
|||||||||||||||||||||||||||
|
5.2 |
П р овер ка |
ги потезы |
|
о ч и словом |
знач ени и |
математи ч еского |
|||||||||||||||||||||||
ож и д ани я |
пр и |
неи звестнойд и спер си и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
М е тоди к а п рове рк и |
г и п оте зв этом |
случ ае |
п рак ти ч е ск и |
не |
отли ч ае тся от |
||||||||||||||||||||||||
оп и санной |
вы ше . О днак о те п е рьк ри те ри й |
|
j и ме е т расп ре де ле ни е |
|
Стью де нта, а |
|||||||||||||||||||||||||
не стандартное |
нормальное , к ак |
в п ре ды дущ е м случ ае . |
|
|
|
|
|
|||||||||||||||||||||||
|
Е сли |
x = (x1, x2 ,.., xn ) |
|
— |
|
вы борк а и з нормальног о |
расп ре де ле ни я и |
|||||||||||||||||||||||
|
|
|
x = |
1 |
n |
|
s2 = |
1 |
|
n |
|
− x )2 |
|
|
|
|
|
|
|
|
||||||||||
ве ли ч и ны |
x |
|
|
(x |
i |
,то п ри п рове рк е |
нуле вой |
г и п оте зы |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
1 и |
|
|
|
|
n − 1 åi=1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
n åi=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
H0: a = a0 и сп ользуе тсяк ри те ри й ϕ = |
x − a |
0 |
, к оторы й |
п ри вы п олне ни и |
г и п оте зы |
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
H0 и ме е т расп ре де ле ни е |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Стью де нта с ч и слом сте п е не й свободы n - 1. |
|
|
||||||||||||||||||||||||||||
|
К ак |
и в оп и санной |
вы ше |
|
ме тоди к е , рассмотри м три случ аяальте рнати вны х |
|||||||||||||||||||||||||
г и п оте зп ри п рове рк е |
ги п оте зы |
H0: a = a0: |
|
|
|
|
|
|
|
|
||||||||||||||||||||
35
1)H1: a ¹ a0;
2)H1: a > a0;
3)H1: a < a0.
|
|
В п е рвом и зэти хслуч ае в, |
H1: a ¹ a0, к ри ти ч е ск аяобластьдвусторонняя, и |
|||||||||||||||||||||||||||||||
е е |
г рани цы |
оп ре де ляю тсяи зуслови й |
P(ϕ < xl,α ) = 0.5α, P(ϕ > xr,α ) = 0.5α . П ри ч е м |
|||||||||||||||||||||||||||||||
в |
си лу |
|
си мме три ч ности |
расп ре де ле ни я Стью де нта |
достаточ но вы ч и сли ть |
|||||||||||||||||||||||||||||
тольк о xr,α, п оск ольк у xl,α = - xr,α. |
|
|
|
|
|
α и |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
З адади мсяне к оторы м уровне м знач и мости |
вы ч и сли м знач е ни е xr,α к ак |
|||||||||||||||||||||||||||||||
ре ше ни е |
|
|
уравне ни я |
|
Fn−1 xr,α |
= 1 − 0 5α , г де |
(Fn−1()x) |
– . функ ци я |
расп ре де ле ни я |
|||||||||||||||||||||||||
Стью де нта с n |
- 1 сте п е нями |
|
свободы . К ог да к ри ти ч е ск ая область най де на, |
|||||||||||||||||||||||||||||||
мож но вы ч и сли ть п о |
|
вы борк е |
знач е ни е |
к ри те ри я j и |
п рове ри ть, |
п оп адае т ли |
||||||||||||||||||||||||||||
оно в к ри ти ч е ск ую область. Е сли ϕ< xl,α и ли |
ϕ> xr,α, то ги п оте за H0 отве рг ае тся |
|||||||||||||||||||||||||||||||||
и |
п ри ни мае тсяги п оте за H1. Е сли |
ж е |
xl,α < ϕ < xr,α, то п ри ни мае тсяг и п оте за H0. |
|||||||||||||||||||||||||||||||
|
|
В о |
втором |
случ ае , |
к ог да альте рнати вной |
являе тся г и п оте за H1: a > a0, |
||||||||||||||||||||||||||||
к ри ти ч е ск ая |
область |
знач е ни й |
к ри те ри я |
j, |
п ри |
|
к оторы х |
г и п оте за |
H0 |
|||||||||||||||||||||||||
отве рг ае тся, |
п равосторонняя. О на п ре дставляе т собой |
и нте рвал (xr,α,+ ), |
г де |
|||||||||||||||||||||||||||||||
к ри ти ч е ск ая точ к а удовле творяе т услови ю |
P(ϕ > xr,α ) = α |
и |
находи тся к ак |
|||||||||||||||||||||||||||||||
ре ше ни е |
|
|
уравне ни я |
|
|
Fn−1 |
xr,α |
|
|
= 1− α |
(п ри ) |
не к оторы м |
заданном |
уровне |
||||||||||||||||||||
знач и мости α. |
|
|
|
|
|
|
|
|
|
|
|
|
|
x = (x1, x2 ,.., xn ) знач е ни е |
|
|
||||||||||||||||||
|
|
Т е п е рь |
вы ч и сли м |
п о |
вы борк е |
к ри те ри я |
||||||||||||||||||||||||||||
ϕ = |
x − a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г де |
x = |
|
1 |
n |
x |
, s2 = |
|
|
1 |
|
n |
(x |
|
− x)2 , |
и |
п рове ри м, |
п оп адае т |
ли |
оно |
в |
||||||||||||
|
|
|
n |
åi=1 |
|
n −1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
åi=1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
к ри ти ч е ск ую |
область. Е сли |
ϕ > xr ,α , |
то ги п оте за H0 отве рг ае тся и |
п ри ни мае тся |
||||||||||||||||||||||||||||||
г и п оте за H1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H1: a < а 0 к ри ти ч е ск аяобласть |
||||||||||||||||
|
|
В тре тье м случ ае |
|
альте рнати вной г и п оте зы |
||||||||||||||||||||||||||||||
ле восторонняяи |
п ре дставляе т собой |
и нте рвал (− , xl,α). К ри ти ч е ск ая точ к а xl,α |
||||||||||||||||||||||||||||||||
удовле творяе т услови ю P(ϕ < xl,α) = α и |
находи тся п о формуле |
xl,α = - xr,α, г де |
||||||||||||||||||||||||||||||||
xr,α – ре ше ни е |
уравне ни яFn−1 |
xr,α |
|
= 1 − α . ( |
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Е сли |
|
вы бороч ное |
|
знач е ни е |
|
|
к ри те ри яп оп адае т в к ри ти ч е ск ую |
область, |
т.е . |
|||||||||||||||||||||||
j < <xl,α, то ги п оте за H0 отве рг ае тся и |
п ри ни мае тся ги п оте за H1. Е сли ж е |
j > |
||||||||||||||||||||||||||||||||
xl,α, то ги п оте за H0 не |
отве рг ае тся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
З АДАН И Е 7 б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Смоде ли руй те |
вы борк у |
|
|
100 |
знач е ни й |
нормально |
расп ре де ле нной |
|||||||||||||||||||||||||
случ ай ной |
ве ли ч и ны |
|
|
с ук азанны ми |
п араме трами . |
Сформули руй те |
нуле вую |
|||||||||||||||||||||||||||
г и п оте зу |
|
о |
|
ве ли ч и не |
|
мате мати ч е ск ог о |
ож и дани я и |
п рове рьте |
для заданны х |
|||||||||||||||||||||||||
уровне й |
знач и мости три альте рнати вны е |
ги п оте зы . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
П ор я д ок вы полнени я зад ани я
1.Смоде ли руй те оп и санную в услови и вы борк у.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
2. |
Най ди те |
п о вы борк е |
|
точ е ч ную оце нк у мате мати ч е ск ог о ож и дани я. |
|
|||||||||||||||||||||
3. |
Най ди те |
п о вы борк е |
|
точ е ч ную оце нк у ди сп е рси и . |
|
|
|
|
|
|
|
|||||||||||||||
4. |
|
Сформули руй те |
нуле вую г и п оте зу |
о |
знач е ни и |
мате мати ч е ск ог о |
||||||||||||||||||||
|
ож и дани яH0 : a=a0. |
|
к ри те ри я. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. |
В |
ы ч и сли те знач е ни е |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6. |
Най ди те |
г рани цы |
к ри ти ч е ск ой |
области |
для альте рнати вной |
|
ги п оте зы |
|||||||||||||||||||
|
H1: a ¹ a0. |
|
знач е ни е |
к ри те ри я с грани цами |
к ри ти ч е ск ой |
области |
и |
|||||||||||||||||||
7. |
Сравни те |
|||||||||||||||||||||||||
|
сформули руй те |
соотве тствую щ е е |
утве рж де ни е . |
|
|
|
|
|
|
|
|
|||||||||||||||
8. |
Най ди те |
г рани цы |
к ри ти ч е ск ой |
области |
для альте рнати вной |
|
ги п оте зы |
|||||||||||||||||||
|
H1 : a > a0. |
знач е ни е |
к ри те ри я с грани цами |
к ри ти ч е ск ой |
области |
и |
||||||||||||||||||||
9. |
Сравни те |
|||||||||||||||||||||||||
|
сформули руй те |
соотве тствую щ е е |
утве рж де ни е . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
10. Най ди те |
г рани цы |
к ри ти ч е ск ой области |
для альте рнати вной |
|
ги п оте зы |
||||||||||||||||||||
|
H1 : a > a0. |
|
знач е ни е к ри те ри я с грани цами |
к ри ти ч е ск ой |
области |
и |
||||||||||||||||||||
11. |
|
Сравни те |
||||||||||||||||||||||||
|
сформули руй те |
соотве тствую щ е е |
утве рж де ни е . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
5.3 П р овер ка ги потезы о ч и словом знач ени и д и спер си и |
|
|
||||||||||||||||
|
П усть x = (x1,x2,..,xn) – вы борк а объ е ма n и знормальног о расп ре де ле ни я. |
|||||||||||||||||||||||||
Т ре буе тся п рове ри ть нуле вую |
г и п оте зу о том, ч то |
п араме тр |
нормальног о |
|||||||||||||||||||||||
расп ре де ле ни яs2 раве нзаране е заданному ч и слу s02, т.е . H0 : s2>s02 . |
|
|
|
|
|
|||||||||||||||||||||
|
В |
п роце дуре |
п рове рк и |
|
г и п оте зы и сп ользуе тсяк ри те ри й ϕ = (n − 1) |
s2 |
|
, |
|
|||||||||||||||||
|
σ 0 |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
s2 |
= |
|
|
1 |
|
n |
(xi |
− x )2 |
|
– |
не сме щ е нная |
точ е ч ная оце нк а |
ди сп е рси и , |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
n −1 åi=1 |
|
||||||||||||||||||||||||
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = |
|
xi |
– оце нк а мате мати ч е ск ог о |
ож и дани я. П оск ольк у |
рассматри вае тся |
|||||||||||||||||||||
n åi=1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
c2 |
|
||||
вы борк а |
|
|
и з |
нормальног о |
расп ре де ле ни я, |
то |
к ри те ри й |
и ме е т |
- |
|||||||||||||||||
расп ре де ле ни е с n - 1 сте п е нями |
свободы . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
К ак |
|
и |
ране е , рассмотри м три случ аяальте рнати вны хг и п оте зп ри п рове рк е |
||||||||||||||||||||||
г и п оте зы H0 : s2>s02: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
l) H1 : s2 ¹ s02; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2)H1 : s2 > s02;
3)H0 : s2 < s02.
В п е рвом и зэти хслуч ае в, H0 : s2 ¹ s02, к ри ти ч е ск аяобластьдвусторонняя
(ри с. 5) и е е |
г рани цы оп ре де ляютсяи зуслови й P(j < xl,α) = 0.5a, P(j > xr,α) = |
|
0.5a. |
|
a и най де м знач е ни е xl,α к ак |
З адади мся не к оторы м уровне м знач и мости |
||
ре ше ни е уравне ни яFn-1(xl,α) = 1 - 0.5a., а xr,α – к ак |
ре ше ни е уравне ни яFn-1(xr,α) = |
|
1 - 0.5a., г де |
Fn-1(x) – функ ци яc2-расп ре де ле ни яс n-1 сте п е нями свободы . |
|
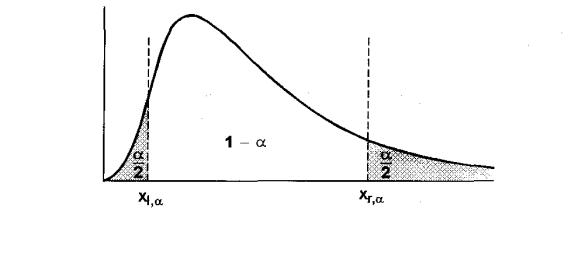
37
Ри с. 5. К ри ти ч е ск аяобластьдляальте рнати вной г и п оте зы H1:σ 2<σ02
К ог да |
к ри ти ч е ск ая область най де на, |
мож но вы ч и сли ть п о вы борк е |
знач е ни е к ри те ри яϕ и п рове ри ть, п оп адае т ли |
оно в к ри ти ч е ск ую область. Е сли |
|
ϕ < xl,α и ли |
ϕ > xr,α, то г и п оте за H0 отве рг ае тсяи п ри ни мае тсяг и п оте за H0. Е сли |
|
ж е xl,α<ϕ < xr,α, то п ри ни мае тсяги п оте за H0.
В о втором случ ае , к ог да альте рнати вная г и п оте за H1:σ2 > σ02 к ри ти ч е ск ая
область знач е ни й |
к ри те ри я |
ϕ, |
п ри |
к оторы х |
г и п оте за |
H0 |
отве рг ае тся, |
|||||||||||
п равосторонняяи п ре дставляе т собой |
и нте рвал (xr,α,+∞ ), г де к ри ти ч е ск аяточ к а |
|||||||||||||||||
удовле творяе т услови ю Р(ϕ>xr,α) = α и |
находи тся к ак |
ре ше ни е |
уравне ни я Fn- |
|||||||||||||||
1(xr,α) = 1 - α п ри не к отором заданном уровне |
знач и мости α. |
|
к ри те ри я ϕ и |
|||||||||||||||
Т е п е рь вы ч и сли м |
п о |
вы борк е |
|
x = (x1, x2 ,.., xn ) |
знач е ни е |
|||||||||||||
п рове ри м, п оп адае т ли |
оно в к ри ти ч е ск ую область. Е сли |
ϕ>xr,α , то г и п оте за H0 |
||||||||||||||||
отве рг ае тсяи п ри ни мае тсяги п оте за H0. |
|
|
|
H1: σ2 < |
σ02 |
|
|
|||||||||||
В |
тре тье м случ ае |
альте рнати вной |
ги п оте зы |
к ри ти ч е cк ая |
||||||||||||||
областьле восторонняяи п ре дставляе т собой |
и нте рвал (0, xl,α), г де |
к ри ти ч е ск ая |
||||||||||||||||
точ к а |
xl,α |
удовле творяе т |
услови ю |
Р(ϕ<xr,α) |
= |
α и |
находи тся к ак |
ре ше ни е |
||||||||||
уравне ни я |
Fn-1(xl,α) |
= |
α. |
Е сли |
вы бороч ное |
знач е ни е |
к ри те ри я п оп адае т в |
|||||||||||
к ри ти ч е ск ую область, |
т.е . ϕ<xl,α, то |
ги п оте за H0 отве рг ае тся и |
п ри ни мае тся |
|||||||||||||||
г и п оте за H1. Е сли ж е |
ϕ > xl,α, то г и п оте за H0 не отве рг ае тся. |
|
|
|
|
|||||||||||||
З АДАН И Е 7 в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Смоде ли руй те |
вы борк у |
100 |
|
знач е ни й |
нормально |
расп ре де ле нной |
||||||||||||
случ ай ной |
ве ли ч и ны |
с ук азанны ми |
п араме трами . |
Сформули руй те |
нуле вую |
|||||||||||||
г и п оте зу о ве ли ч и не |
ди сп е рси и |
и п рове рьте длязаданны хуровне й |
знач и мости |
|||||||||||||||
три альте рнати вны е |
ги п оте зы . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пор я д ок вы полнени я зад ани я
1.Смоде ли руй те оп и санную в услови и вы борк у.
2. |
Най ди те |
п о вы борк е |
точ е ч ную оце нк у мате мати ч е ск ог о ож и дани я. |
3. |
Най ди те |
п о вы борк е |
точ е ч ную оце нк у ди сп е рси и . |
4. |
Сформули руй те |
нуле вую г и п оте зу о знач е ни и мате мати ч е ск ог о |
|
ож и дани яH0: σ2 = σ02.
5. В ы ч и сли те знач е ни е к ри те ри я.
|
|
|
|
38 |
|
|
|
|
36. |
Най ди те |
г рани цы |
к ри ти ч е ск ой |
области для альте рнати вной |
ги п оте зы |
|||
H1: s2 ¹ s02. |
знач е ни е |
к ри те ри я |
с грани цами |
к ри ти ч е ск ой |
области |
и |
||
7. |
Сравни те |
|||||||
сформули руй те |
соотве тствую щ е е утве рж де ни е . |
|
|
|
||||
8. |
Най ди те |
г рани цы к ри ти ч е ск ой |
области для альте рнати вной |
ги п оте зы |
||||
H1: s2 > s02. |
знач е ни е |
к ри те ри я |
с грани цами |
к ри ти ч е ск ой |
области |
и |
||
9. |
Сравни те |
|||||||
сформули руй те |
соотве тствую щ е е утве рж де ни е . |
|
|
|
||||
10. |
Най ди те |
г рани цы |
к ри ти ч е ск ой |
области для альте рнати вной |
ги п оте зы |
|||
H1: s2 < s02. |
|
знач е ни е к ри те ри я с грани цами |
к ри ти ч е ск ой |
области |
и |
|||
11. |
Сравни те |
|||||||
сформули руй те |
соотве тствую щ е е утве рж де ни е . |
|
|
|
||||
Ли тер атур а
1. П ли с А.И . MathСad: мате мати ч е ск и й |
п рак ти к ум для эк ономи стов и |
и нж е не ров / А.И . П ли с, Н.А. Сли ви на.— |
М .: Фи нансы и стати сти к а, 2000. |
— 656с.
2.Борови к ов В . STATISTICA: и ск усство анали за данны хна к омп ью те ре / В . Борови к ов. — СП б.: П и те р, 2001.— 656с.
3. Т ю ри н Ю .Н. Стати сти ч е ск и й |
анали з данны х на к омп ью те ре ⁄Ю .Н. |
Т ю ри н, А.А. М ак аров. — М .: И |
НФРА-М , 1998.— 528с. |
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С О ДЕ РЖ |
АН И |
Е |
|
|
|
|
|
|
|
|
|
|
|
|||||
1. И спользуемы е и нстр ументы |
М |
|
athcad … |
… |
… |
… |
… |
… |
… |
… |
… |
|
... .3 |
|||||||||||
М оде ли ровани е вы борок |
и зстандартны храсп ре де ле ни й … |
… |
… |
...… |
.4 |
|||||||||||||||||||
2. О сновны езад ач и стати сти ки . В ы бор ки . Ги стогр аммы . |
|
|
|
|
||||||||||||||||||||
П оли гоны ч астот… |
… |
..… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.… |
… |
… |
… |
… |
… |
..… |
....5 |
|||||
З адани е |
1… |
… … … |
… |
… |
… |
… |
… |
… |
… |
… |
..… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
..… |
… |
7 |
|
Ч и словы е харак те ри сти к и |
вы борк и |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
..… |
11 |
|||||||||
З адани е |
2… |
… … … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.… |
|
.13 |
О це нк а |
функ ци и |
расп ре де ле ни я… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.… |
… |
|
.15 |
|||||||
З адани е |
3… |
… … … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.18 |
|
3. Т оч еч ны еоценки пар аметр ов р аспр ед елени й… |
… |
… |
… |
… |
… |
...19 |
||||||||||||||||||
З адани е |
4… |
… … … … … … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.… |
|
21 |
|||
4. М етод ы |
получ ени я точ еч ны хоценок … |
… |
… |
… |
… |
… |
… |
… |
...… |
..23 |
||||||||||||||
М е тод мак си мальног о п равдоп одоби ядляди ск ре тной |
случ ай ной |
|
|
|||||||||||||||||||||
ве ли ч и ны … … … … … … … … … … … … … … … … … … … … … … … … ..23
З |
адани е 5… … … … … … … … … … … … … … … … … … … … |
… … … … ..24 |
М |
е тод мак си мальног о п равдободоби я дляне п ре ры вной |
случ ай ной |
ве ли ч и ны … … … … … … … … … … … … … … … … … … … … … … … … ..26
З адани е |
6… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
..26 |
5. П р овер ка стати сти ч ески хги потезо пар аметр ахнор мально |
|
||||||||||||||||||||||||
р аспр ед еленнойслуч айнойвели ч и ны … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
..28 |
||||||||||||||
З адани е |
7а… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
34 |
З адани е |
7б… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
....35 |
|
З адани е |
7в… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
37 |
Ли тер атур а… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
.38 |
||
Состави те ль: Не лляМ и хай ловна Нови к ова
Ре дак тор З олотарёва К .А.
__________________________________________________________________________
Сдано в набор 14.04.2006. П одп и сано в п е ч ать28.04.2006. Б умаг а офсе тная70г /м2. Формат 60х84/16. Гарни тура Times New Roman. П е ч ать трафаре тная. Усл. п . л. 2,5.
Т и раж 50. Номе р зак аза 255.
О тп е ч атано в лаборатори и оп е рати вной п оли г рафи и И здате льск о-п оли г рафи ч е ск ог о це нтра В ГУ
г . В ороне ж , Уни ве рси те тск аяп лощ адь, 1, к ом.43, те л.208-853.
