
Лабораторные работы по ТВиМС
.pdf11 |
|
|
Ука за ние. В п ри ве де нном фраг ме нте |
250 вы бороч ны хзнач е ни й |
сохране ны |
в масси ве с и ме не м ξ. П ре ж де ч е м |
п ри ступ ать к г руп п и ровк е |
вы борк и , |
не обходи мо уп орядоч и ть вы бороч ны е знач е ни я в п орядк е и х возрастани я. Эту
оп е раци ю |
вы п олняе т функ ци я sort(ξ). Груп п и ровк а п рои зводи тся с п омощ ью |
||||||||
функ ци и |
hist(x, ξ), г де |
х – масси в, |
соде рж ащ и й |
знач е ни я се ре ди н и нте рвалов |
|||||
г руп п и ровк и . П ре ж де |
ч е м обрати ться к |
функ ци и |
hist(x,ξ), |
не обходи мо |
|||||
вы ч и сли ть |
се ре ди ны |
и нте рвалов |
г руп п и ровк и |
и |
п ри свои ть |
и х знач е ни я |
|||
эле ме нтам |
масси ва x. |
З нач е ни я |
функ ци и |
hist(x,ξ) |
– |
ве к тор, |
к омп оне нты |
||
к оторог о равны к оли ч е ству эле ме нтов масси ва ξ, п оп авши хв и нте рвал
При ме р вы п олне ни язадани я
При ме рны й вари ант вы п олне ни язадани ядлявсе й вы борк и дляm = 10, 20, 100 п ри ве де нвы ше .
2.2Ч и словы ехар актер и сти ки вы бор ки
П оказатели |
полож ени я . |
Сре дне е |
знач е ни е |
вы борк и |
вы ч и сляе тся п о |
|||||||||
формуле |
|
|
|
|
1 |
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x = |
å xi . |
|
|
|
|
|
||||
|
|
|
|
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
В |
Mathcad |
для вы ч и сле ни я вы бороч ног о |
сре дне г о знач е ни я вы борк и , |
|||||||||||
сохране нной |
в |
матри це |
А, |
п ре дназнач е на функ ци я mean(A). |
Выбо ро ч но й |
|||||||||
ква нт илью уровнярназы вае тсяре ше ни е |
уравне ни я |
|
|
|
|
|||||||||
|
|
|
|
Fn (x) = p, |
|
|
|
|
|
|||||
г де Fn(x) — вы бороч наяфунк ци ярасп ре де ле ни я. |
|
уравне ни яFn(x) = 0.5, т.е . |
||||||||||||
В |
ч астности , выбо ро ч на ямедиа на е стьре ше ни е |
|||||||||||||
вы бороч ная ме ди ана — |
это |
вы бороч ная к ванти ль уровня 0.5. |
В ы бороч ная |
|||||||||||
ме ди ана разби вае т вы борк у |
п оп олам: |
сле ва и |
сп рава от |
не е |
ок азы вае тся |
|||||||||
оди нак овое |
ч и сло эле ме нтов вы борк и . |
Е сли ч и сло |
эле ме нтов вы борк и |
ч е тно, |
||||||||||
n = 2k, |
то вы бороч ную ме ди ану оп ре де ляют п о формуле :(xk+xk+1)/2, г де |
xk, xk+1 |
||||||||||||
– k-е и |
(k+1)-е |
вы бороч ны е |
знач е ни я и звари аци онног о ряда. П ри не ч е тном |
|||||||||||
объ е ме |
вы борк и |
(n=2k+1) в к ач е стве знач е ни я ме ди аны п ри ни маю т ве ли ч и ну |
||||||||||||
xk+1. В |
Mathcad для вы ч и сле ни я вы бороч ной ме ди аны вы борк и , сохране нной в |
|||||||||||||
матри це А, п ре дназнач е на функ ци яmedian(A).
К |
п ок азате лям |
п олож е ни я |
относятся |
ми ни мальны й |
и |
мак си мальны й |
|||||
эле ме нты вы борк и , |
а так ж е |
ве рхняя и |
ни ж няя к варти ли |
(они |
ог рани ч и вают |
||||||
зону, в к оторой сосре доточ е ны 50% эле ме нтов вы борк и ) |
|
|
вы борк и , |
||||||||
Для вы ч и сле ни я ми ни мальног о и |
мак си мальног о эле ме нтов |
||||||||||
разме щ е нной в матри це А, в Mathcad п ре дназнач е ны |
соотве тстве нно функ ци и |
||||||||||
min(A) и max(A). |
р азбр оса. |
К |
п ок азате лям |
разброса относятся |
ди сп е рси я |
||||||
П оказатели |
|||||||||||
вы борк и |
(вы бороч ная ди сп е рси я), стандартное отк лоне ни е , размах вы борк и , |
||||||||||
ме ж к варти льны й |
размах, |
к оэффи ци е нт эк сце сса |
(вы бороч ны й |
эк сце сс). |
|||||||
Выбо ро ч но йдис перс иейназы вае тсяве ли ч и на
1 ån (xi − x)2. n i=1
О днак о в стати сти к е ч ащ е в к ач е стве вы бороч ной ди сп е рси и

|
|
12 |
|
и сп ользуе тсяве ли ч и на |
|
|
|
|
1 |
n |
|
s2 = |
å(xi − x)2. |
||
|
|||
|
n −1 i=1 |
||
В Mathcad дляоп ре де ле ни яди сп е рси и вы борк и , сохране нной в матри це A, п ре дназнач е на функ ци яvar(A), а ве ли ч и ну s2 мож но вы ч и сли тьп о формуле :
s2 = n1−1var(A).
Ст а нда рт но е о т кло нение рассч и ты вае тсяп о формуле :
σˆ = 
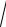 s2 .
s2 .
Ра зма хвыбо рки вы ч и сляе тсяп о формуле |
R= xmax-xmin |
75%-ная к варти ль, |
||||||||||
М еж ква рт ильный ра зма х раве н x0.75-x0.25 |
г де x0.75 – |
|||||||||||
ре ше ни е уравне ни яFn(x0.75) = 0.75, x0.25 – 25%-наяк варти ль, ре ше ни е |
уравне ни я |
|||||||||||
Fn(x0.25) = 0.25. |
|
|
|
|
|
|
|
|
|
|
|
|
В ы бороч ны й эк сце сс |
оп ре де ляе тся |
сле дующ и м |
образом. |
Снач ала |
||||||||
оты ск и вае тсяве ли ч и на вы бороч ног о це нтральног о моме нта 4-г о п орядк а |
||||||||||||
|
μˆ4 = 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
å xi −( x 4 . ) |
|
|
|
|
|||||||
|
n |
i=1 |
|
|
|
|
|
|
|
|
|
|
А зате м п о сле дую щ е й |
формуле |
|
вы ч и сляе тсявы бороч ны й эк сце сс: |
|||||||||
|
ˆ |
|
|
2 |
) |
−2 |
− 3. |
|
|
|
|
|
|
E = μˆ4 (s |
|
|
|
|
|
|
|
||||
П оказатели |
аси мметр и и . |
На |
|
|
основани и |
эти х п ок азате ле й |
и зуч аю т |
|||||
и нформаци ю о |
си мме три и |
расп ре де ле ни я вы бороч ны х данны х ок оло це нтра |
||||||||||
вы борк и . Сю да в п е рвую оч е ре дьотноси тсяк оэффи ци е нт аси мме три и , к оторы й вы ч и сляе тсяп о формуле
|
|
1 |
n |
|
|
μˆ3 = |
å(xi − x)3 |
||
|
n |
|||
г де |
|
i=1 |
— вы бороч ны й це нтральны й моме нт 3-г о п орядк а, а |
|
σ – |
стандартное |
отк лоне ни е , формула для вы ч и сле ни я к оторог о п ри ве де на |
||
вы ше . |
|
|
|
|

|
13 |
|
|
З АДАН И Е 2 |
|
|
Для вы борк и , сформи рованной в п ре ды дущ е м |
задани и , вы ч и сли те все |
оп и санны е вы ше вы бороч ны е харак те ри сти к и . |
|
|
|
П орядок вы п олне ни язадани я |
|
1. |
П роч ти те сохране нны й ране е фай л, соде рж ащ и й |
вы борк у. |
2. |
В ы ч и сли те мак си мальны й и ми ни мальны й эле ме нты и размахвы борк и . |
|
3.Рассч и тай те вы бороч ное сре дне е .
4.Най ди те ме ди ану.
5. |
В ы ч и сли те |
вы бороч ную ди сп е рси ю и стандартное отк лоне ни е . |
|
6. |
Най ди те вы бороч ны е моме нты 3-г о и 4-г о п орядк ов. |
||
7. |
В ы ч и сли те |
вы бороч ны й |
эк сце сс. |
8. |
О п ре де ли те к оэффи ци е |
нт аси мме три и . |
|
П р и мер вы полнени я |
зад ани я |
|
Ни ж е |
п ре дставле н фраг ме нт рабоч е г о док уме нта Mathcad, соде рж ащ и й |
|
вы ч и сле ни е |
харак те ри сти к |
вы бороч ны хданны х, п ри ве дённы хв нач але разде ла. |
Ука за ние. В |
Mathcad не т встрое нны х функ ци й для вы ч и сле ни я вы бороч ны х |
моме нтов. |
Для оп ре де ле ни я сре дне к вадрати ч ног о отк лоне ни я в Mathcad |
п ре дназнач е на функ ци я

14 |
|
|
Рассч и ты вае мое с е е п омощ ью знач е ни е |
сре дне к вадрати ч ног о |
отк лоне ни я |
отли ч но от оп ре де ле нног о вы ше , п оэтому |
сре дне к вадрати ч ное |
отк лоне ни е |
сле дуе т вы ч и слятьк ак |
|
|
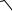
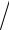 s 2 .
s 2 .
2.3 О ценка функци и р аспр ед елени я
Рассмотри м ме тоды |
оце ни вани я функ ци и расп ре де ле ни яFξ(x) случ ай ной |
|||||
ве ли ч и ны , о к оторой |
и зве стно, ч то она не п ре ры вна. |
|
||||
П усть x={x1,x2,..,xn} |
– совок уп ность вы бороч ны х знач е ни й случ ай ной |
|||||
ве ли ч и ны |
ξ, |
т.е . вы борк а и зслуч ай ной |
ве ли ч и ны ξ. |
Расп олож и м наблю де ни я |
||
x1,x2,..,xn |
в |
п орядк е |
и х |
возрастани я. |
О бознач и м |
новую уп орядоч е нную |
п осле довате льность – вари аци онны й ряд - x`1,x`2,..,x`n, x`1<x`2<..<x`n. П о этому
вари аци онному |
ряду |
п острои м |
сле дую щ ую |
|
не убы ваю щ ую |
|
ступ е нч атую |
|||||||||||||||||
функ ци ю : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì0,x £ x1′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ïk |
,x¢k−1 £ x £ x¢k ,k =1,2,...,n, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= í |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Fn (x) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
ïn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï1,x > x¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
î |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И з п ри ве де нной |
|
вы ше |
формулы |
ви дно, |
ч то |
|
|
|
ˆ |
п ре те рп е вае т |
в |
|||||||||||||
|
функ ци яFn (x) |
|||||||||||||||||||||||
к аж дой |
точ к е |
вари аци онног о ряда ск ач ок , равны й |
п о ве ли ч и не |
1/n. Е сли |
к ак ая- |
|||||||||||||||||||
ни будь точ к а вари аци онног о ряда п овторяе тся т |
раз(т |
точ е к |
вари аци онног о |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
в этой |
точ к е |
раве нт /п. |
|
|
|
|
|
||||
ряда совп адаю т), то ск ач ок функ ци и Fn (x) |
|
|
|
|
|
|||||||||||||||||||
Функ ци яFn(x) назы вае тсяэмпирич ес ко йфункциейра с пределения. |
|
|
|
|
|
|||||||||||||||||||
За меч а ние. |
Эмп и ри ч е ск ая |
функ ци я расп ре де ле ни я |
ˆ |
|
|
|
|
|
не |
|||||||||||||||
Fn (x) зави си т |
||||||||||||||||||||||||
тольк о от x, но и |
от все й вы борк и |
x. |
Ч тобы обрати ть вни мани е на этот фак т, |
|||||||||||||||||||||
буде м |
обознач ать эмп и ри ч е ск ую |
функ ци ю |
расп ре де ле ни я |
ч е ре з |
n |
( F, xˆ)x |
||||||||||||||||||
|
. |
|||||||||||||||||||||||
И ме нно |
n ( |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
функ ци и |
расп ре де ле ни я |
|||||||
F, x)x п ри ни маю т за оце нк у те оре ти ч е ск ой |
||||||||||||||||||||||||
F(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О стае тся |
|
вы ясни ть, |
наск ольк о |
хорошо |
эмп и ри ч е ск ая |
функ ци я |
||||||||||||||||||
расп ре де ле ни яап п рок си ми руе т те оре ти ч е ск ую функ ци ю расп ре де ле ни я. |
|
|
— |
|||||||||||||||||||||
Е сли |
Fξ(x) |
– те оре ти ч е ск ая |
функ ци я |
расп ре де ле ни я, |
a |
Fn(x) |
||||||||||||||||||
эмп и ри ч е ск ая функ ци я расп ре де ле ни я, |
п острое нная п о |
заданной |
вы борк е |
xˆ |
||||||||||||||||||||
знач е ни й случ ай ной |
ве ли ч и ны |
ξ, |
|
то |
в |
к ач е стве |
ме ры |
|
расхож де ни я |
|||||||||||||||
те оре ти ч е ск ой |
и |
эмп и ри ч е ск ой |
функ ци й |
расп ре де ле ни явозьме м ве ли ч и ну: |
|
|||||||||||||||||||
ˆ |
|
Fn (x) − Fξ (x) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Dn (x) = sup |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта функ ци я от |
вы бороч ны х знач е ни й |
х назы вае тся с т а т ис т ико й |
|||
К о лмо го ро ва . |
Сле дуе т |
п омни ть, |
ч то Dn (xˆ) случ ай ная ве ли ч и на и |
ч то е е |
|
расп ре де ле ни е |
не зави си т от |
не и зве стной |
те оре ти ч е ск ой |
функ ци и |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расп ре де ле ни я Fξ(x), |
е сли |
|
она не п ре ры вна. Боле е |
тог о, |
сп раве дли ва те оре ма |
||||||||||||||||||||||||
К олмог орова: |
е сли |
функ ци я расп ре де ле ни я |
Fξ(x) |
случ ай ной |
|
ве ли ч и ны |
ξ |
||||||||||||||||||||||
не п ре ры вна, a Fn(x) – е е вы бороч наяфунк ци ярасп ре де ле ни я, то п ри |
n→∞ |
|
|||||||||||||||||||||||||||
æ |
|
|
|
|
|
|
|
z |
ö |
ì |
z £ |
, 0 |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ˆn |
|
|
|
|
|
ï |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
çsup |
|
- |
n |
x |
|
<FP |
|
|
|
x÷ ®F K z) =( í |
|
) 2 (2 |
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
è x |
|
|
|
|
|
|
|
|
n ø |
ï |
å - |
e−k2 z |
k z > |
|
. 0 |
|
|
, |
|
|
( )1 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
îk =−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функ ци яK(z) п ре дставляе т собой |
функ ци ональны й |
ряд, к оторы й |
|
сле дуе т |
|||||||||||||||||||||||||
п ротабули ровать. |
Сразу |
обрати м вни мани е |
на |
то, |
ч то |
этот |
ряд |
|
сходи тся |
||||||||||||||||||||
абсолю тно длявсе хz>0, но не равноме рно на п роме ж утк е |
[0, +∞ ]. Это означ ае т, |
||||||||||||||||||||||||||||
ч то длядости ж е ни язаданной |
точ ности п ри вы ч и сле ни и |
K(z) ч и сло N ч ле нов в |
|||||||||||||||||||||||||||
соотве тствую щ е й |
ч асти ч ной |
сумме зави си т от z. Е сли |
ε – тре буе мая точ ность |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é1 |
|
|
|
|
|
|
|
ù |
|
|
|
|
|
|
|
|
|
ч и сло N вы ч и сляе тся п о |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|||||||||
вы ч и сле ни я К (z), |
то |
формуле |
N = ê |
|
|
|
|
ln |
|
ú + 1, |
г де |
||||||||||||||||||
|
2 |
ε |
|||||||||||||||||||||||||||
си мволом [ ] обознач е на це лаяч астьч и сла. |
|
|
|
|
|
ë z |
|
|
û |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
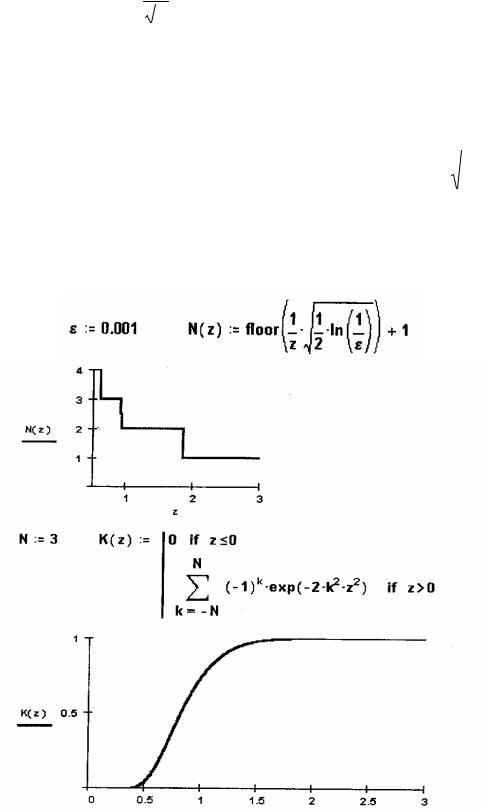
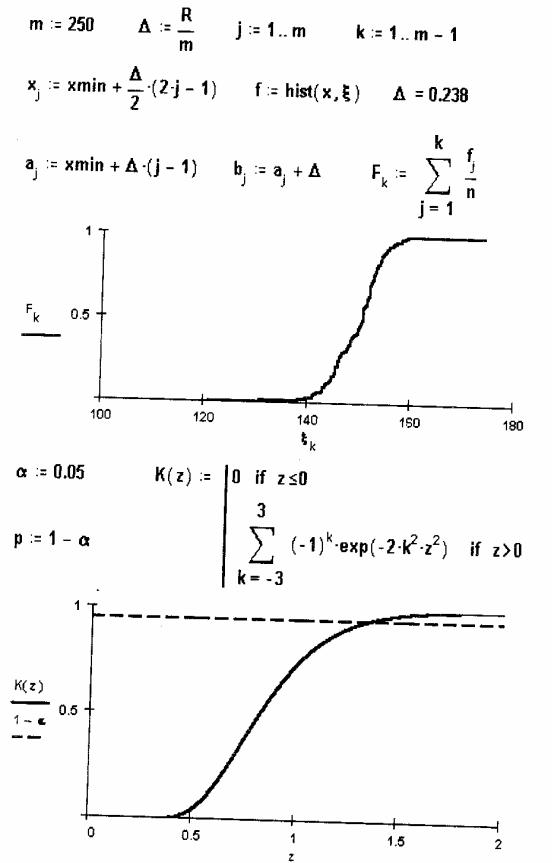
Ни ж е |
|
п ри ве де н |
фраг ме нт |
рабоч е г о |
док уме нта |
Mathcad, |
|
соде рж ащ и й |
|||||||||||||||||||||
п ри бли ж е нное |
оп ре де ле ни е |
функ ци и |
K(z) |
для ε |
= |
0.001, |
|
|
N |
|
= 3, |
и |
|||||||||||||||||
соотве тствую щ и е |
г рафи к и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

|
|
16 |
И зп ри ве де нны х в док уме нте |
г рафи к ов ви дно, ч то для малы х z ве ли ч и ну |
|
K(z) мож но п олож и ть равной |
нулю , а для z > 2 мож но сч и тать K(z) равной |
|
е ди ни це . |
α |
|
З адади мся ве роятностью |
так ой , ч то собы ти е , п рои сходящ е е с |
|
ве роятностью 1-α, п ре дставляе тсяп рак ти ч е ск и достове рны м. В ы ч и сли м к оре нь Zα уравне ни я1 – K(z) =α, тог да не раве нство:
ˆ |
|
zα |
|
|
ˆ |
zα |
|
|
|
|
|
|
|||
Fn x |
|
|
|
|
|
ξ |
) ( n (x) +FF( |
|
) |
x |
< − |
< |
|
|
|
|
|
n |
n |
|
к 1-α. |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
вы п олняе тсядлявсе хде й стви те льны ххс ве роятностью , бли зк ой |
|||||||||||||||
Т ак и м |
образом, |
в |
ок ре стности эмп и ри ч е ск ой |
|
функ ци и |
расп ре де ле ни я |
|||||||||
п острое н |
"к ори дор", |
в |
к отором |
ле ж и т |
и сти нная, |
те оре ти ч е ск ая функ ци я |
|||||||||
расп ре де ле ни яFξ(x). Сростом п "ши ри на" этог о к ори дора стре ми тсяк нулю .
В ме сто |
эмп и ри ч е ск ой |
функ ци и |
расп ре де ле ни я |
буде м и сп ользовать |
|||||||
функ ци ю нак оп ле нны хотноси те льны хч астот, п оск ольк у |
ˆ |
|
|||||||||
Fn (x) = Fk, для x (ξk- |
|||||||||||
1,ξk] и знач е ни яфунк ци й |
совп адают вне |
п роме ж утк а [xmin, xmax]. |
|||||||||
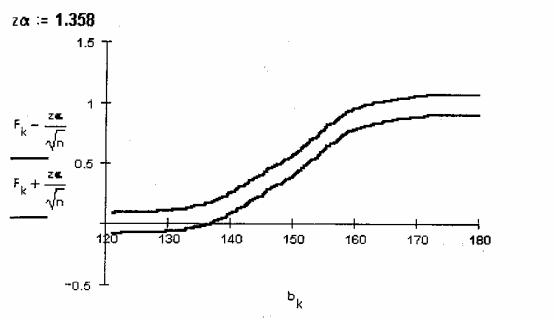
На сле дую щ е й |
страни це п ри ве де нфраг ме нт рабоч е г о док уме нта Mathcad с |
||||||||||
п острое ни е м |
95%-ног о |
"к ори дора" для функ ци и |
расп ре де ле ни я случ ай ной |
||||||||
ве ли ч и ны п о п ри ве де нной вы борк е . |
|
|
|
|
|
||||||
Ука за ние. |
К ак |
уж е |
отме ч алось вы ше , в к ач е стве эмп и ри ч е ск ой функ ци и |
||||||||
расп ре де ле ни я |
и сп ользована |
эмп и ри ч е ск ая функ ци я нак оп ле нны х ч астот. |
|||||||||
З аме ти м, ч то |
Mathcad вме сто |
г рафи к а ступ е нч атой |
функ ци и |
строи т ломаную |
|||||||
ли ни ю , сое ди няя |
"ступ е ньк и " |
ве рти к альны ми |
отре зк ами |
п рямы х. К оре нь |
|||||||
уравне ни я 1 – К (z) |
=α |
п рощ е |
все г о |
най ти г рафи ч е ск и , |
и сп ользуя оп е раци ю |
||||||
Trace п унк та |
|
Graph ме ню Format), к ак точ к у |
п е ре се ч е ни я г рафи к а K(z) и |
||||||||
п рямой у = 1-α. Ни ж е п ри ве де н фраг ме нт ок на Mathcad с ок ном отображ е ни я к оорди нат точ к и п е ре се ч е ни я.
17
18
Для |
оце нк и |
п лотности |
расп ре де ле ни я |
случ ай ной |
ве ли ч и ны |
мож но |
||||||||||
восп ользоваться п оли г оном ч астот, к оторы й п ре дставле н вы ше . |
П ри не |
оч е нь |
||||||||||||||
строг и х ог рани ч е ни ях док азано, ч то |
вы бороч ная п лотность ве роятносте й , т.е . |
|||||||||||||||
п оли г он ч астот, с |
ростом |
объ е ма |
вы борк и |
до бе ск оне ч ности |
стре ми тся к |
|||||||||||
и сти нной , те оре ти ч е ск ой |
п лотности |
|
расп ре де ле ни я и ссле дуе мой |
случ ай ной |
||||||||||||
ве ли ч и ны . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З АДАН И Е 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
П острой те длявы борк и , сформи рованной |
в задани и 1, 95%-ны й |
"к ори дор" |
||||||||||||||
дляфунк ци и |
расп ре де ле ни яи ссле дуе мой |
случ ай ной |
ве ли ч и ны . |
|
|
|
|
|||||||||
П ор я д ок вы полнени я |
зад ани я |
|
|
|
|
|
|
|
|
|
|
|
||||
1. П роч и тай те |
фай л, сохране нны й |
п ри вы п олне ни и задани я1. |
|
|
||||||||||||
2. О п ре де ли те |
стати сти к у К олмог орова — |
функ ци ю |
K(z) и |
п острой те е е |
||||||||||||
г рафи к . |
|
|
|
|
|
α. |
|
|
|
|
|
|
|
|
|
|
3. О п ре де ли те |
знач е ни е ве ли ч и ны |
|
|
|
|
|
|
|
|
|
||||||
4. Ре ши те г рафи ч е ск и уравне ни е |
1 - K(z) = α. |
|
|
|
|
|
|
|
||||||||
5. П острой те "к ори дор" дляте оре ти ч е ск ой |
функ ци и расп ре де ле ни я. |
|
||||||||||||||
П р и мер вы полнени я |
зад ани я |
|
|
|
|
|
|
|
|
|
|
|
||||
П ри ме р |
п острое ни я 95%-ног о |
"к ори дора" функ ци и |
расп ре де ле ни я для |
|||||||||||||
и ссле дуе мой |
во все хп ри ме рахэтог о разде ла вы борк и |
250 знач е ни й |
случ ай ной |
|||||||||||||
ве ли ч и ны п ри ве де нвы ше . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Т О Ч Е Ч Н Ы |
Е О Ц Е Н КИ |
П АРАМ |
Е Т РО В РАС П РЕ ДЕ ЛЕ Н И Й |
|
||||||||||||
П ре дп олож и м, ч то функ ци ярасп ре де ле ни я случ ай ной |
ве ли ч и ны |
ξ зави си т |
||||||||||||||
от не и зве стног о п араме тра θ: P(ξ<X) |
= |
Fξ(x,θ). Е сли |
x1,x2,..,xn |
– вы борк а и з |
||||||||||||
г е не ральной |
совок уп ности |
случ ай ной |
ве ли ч и ны ξ, |
то |
оце нк ой |
θˆ п араме тра θ |
||||||||||
назы вае тся п рои звольная функ ци я от вы бороч ны х знач е ни й |
θˆ =θˆ ( |
x1,x2,..,xn). |
||||||||||||||
К оне ч но, |
и сп ользуе мы е |
на |
п рак ти к е |
оце нк и |
θˆn (x1,x2,..,xn) |
не |
совсе м |
|||||||||
п рои звольны е функ ци и : они обладаю т рядом свой ств, |
к оторы е |
обе сп е ч и ваю т в |
||||||||||||||

|
|
|
|
19 |
|
|
|
|
не к отором |
смы сле |
оп ти мальное |
и звле ч е ни е |
и нформаци и и з |
вы борок . |
|||
Рассмотри м эти свой ства. |
|
|
|
|
|
|||
Т оч еч ны еоценки математи ч еского ож и д ани я |
|
|
||||||
Сле дуе т отме ти ть, ч то знач е ни е |
оце нк и |
θˆ ме няе тсяот вы борк и к |
вы борк е |
|||||
и , знач и т, |
θˆ |
е сть |
случ ай ная ве ли ч и на. |
Е сте стве нно п отре бовать, |
ч тобы |
|||
знач е ни яэтой |
случ ай ной ве ли ч и ны |
в больши нстве |
эк сп е ри ме нтов бы ли |
бли зк и |
||||
к знач е ни ю оце ни вае мог о п араме тра. Этог о мож но дости г нуть, е сли длялю бог о
знач е ни я |
n |
мате мати ч е ск ое |
ож и дани е |
ве ли ч и ны |
|
θˆn |
равно |
и сти нному |
||||||||||||
(те оре ти ч е ск ому) знач е ни ю п араме тра θˆ : Mθˆn = θ. |
|
|
|
|
|
|
|
|||||||||||||
О це нк и |
|
θˆn , |
удовле творяющ и е |
услови ю |
|
Mθˆn =θ, |
|
назы ваю тся |
||||||||||||
нес мещ енными. Не сме щ е нностьоце нк и |
означ ае т, ч то эта оце нк а не |
не се т в се бе |
||||||||||||||||||
си сте мати ч е ск ой |
оши бк и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оце нк и , — |
||||
Е щ е |
одно |
важ ное |
свой ство, |
к оторы м |
долж ны |
обладать |
||||||||||||||
состояте льность. |
О це нк а θˆn назы вае тся с о с т о ят ельно й оце нк ой |
п араме тра θ, |
||||||||||||||||||
е сли длялю бог о ε>0 сп раве дли во: lim P(|θn^-θ|<ε) =1. |
|
|
|
|
|
|
||||||||||||||
П оясни м |
смы сл п осле дне г о |
раве нства. П усть ε>0 – к ак |
уг одно малое |
|||||||||||||||||
п олож и те льное |
ч и сло. Т ог да с ростом п расте т наша уве ре нность в том, ч то |
|||||||||||||||||||
знач е ни е |
оце нк и |
θˆn отли ч ае тся от и сти нног о знач е ни я п араме тра θ не боле е |
||||||||||||||||||
ч е м на ве ли ч и ну ε, |
т.е . с ростом |
объ е ма вы борк и |
уве ли ч и вае тся точ ность |
|||||||||||||||||
ре зультата. П равда, |
зде сь п ри ходи тся отой ти |
от |
тради ци онног о п оняти я |
|||||||||||||||||
точ ности : |
не т г аранти и , |
ч то |
|θˆn -θ|<ε, |
однак о |
утве рж дае тся, |
ч то, |
нач и ная с |
|||||||||||||
не к оторог о п, собы ти е |θˆn -θ|<ε станови тсяп рак ти ч е ск и достове рны м. |
||||||||||||||||||||
В ообщ е |
г оворя, дляоце нк и одног о и тог о ж е |
п араме тра мож но п ри думать |
||||||||||||||||||
мног о разли ч ны х |
не сме щ е нны х |
и |
состояте льны х |
оце нок . |
Рассмотри м |
|||||||||||||||
не ск ольк о п ри ме ров. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
П усть |
x1, |
x2, .., xn |
– |
вы борк а |
и з |
г е не ральной |
|
совок уп ности , |
||||||||||||
соотве тствую щ е й |
случ ай ной |
ве ли ч и не |
ξ |
с |
не и зве стны м |
мате мати ч е ск и м |
||||||||||||||
ож и дани е м Mξ=θ и и зве стной |
ди сп е рси е й Dξ=σ2. П острои м не ск ольк о оце нок |
|||||||||||||||||||
не и зве стног о |
п араме тра Mξ=θ. Нап ри ме р, е сли |
θˆn |
(1) =x1, то |
Mθˆn |
(1) =x1, т.е . |
|||||||||||||||
рассматри вае мая оце нк а являе тся нес мещ енно й о ценко й. П оск ольк у знач е ни е θˆn (1) =x1 вообщ е не зави си т от объ е ма вы борк и n, то оце нк а θˆn (1) не являе тся с о с т о ят ельно й. Рассмотри м друг ую оце нк у:
θˆ(2) = x1 + 2x2 + ... + nxn . n n(n +1)
2
Най де м
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
æ |
ξ |
+ 2ξ |
|
+ ... + nξ |
|
ö |
|
|||
Mθˆn(2) = M |
ç |
|
n |
÷ |
= |
||||||||
ç |
1 |
|
|
2 |
|
|
|
÷ |
|||||
|
|
|
ç |
|
|
n(n +1) |
|
÷ |
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
2 |
|
×θ (1 + 2 + ... + n) = |
|||
|
|
|
|
|
|
|
|
= |
|
||||
|
|
|
|
|
|
|
|
n(n +1) |
|||||
= |
2θ |
× n(n +1) |
=θ , |
|
|
|
|||||||
n(n +1) |
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
т.е . и ме е м не сме щ е нную оце нк у. П рове ри м е е состояте льность.
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Dθˆn |
)(2 |
ç |
|
|
1 |
2 |
2 |
|
...+ + nξ+ ÷ |
ξ |
|
|
|
ξ4 |
|
|
|
σ |
|
2 |
|
2 |
2 |
2 |
|
|||||||||||
= Dç |
|
|
|
|
|
|
|
|
|
|
n |
÷ |
= |
|
|
|
|
|
|
|
n |
|
) = |
...+× |
|
+ 2 |
+(1 |
|||||||||
|
|
|
|
n n(+ |
)1 |
|
|
|
|
n |
2 |
n(+ |
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
)1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
4σ 2 |
è |
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ )1 |
|
|
|
2(n)(+1)1 2 |
|
2(n |
n n |
|
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
σ |
. |
|
|
|
|
|
|
|
|
|||
n |
2 |
n(+ |
2 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
)1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n n + )1 3 ( |
|
|
|
|
|
|
|
|||||||||||||
П оск ольк у |
Dθˆn |
)(2→ 0 п ри |
|
n®∞ , то, сог ласно зак ону больши х ч и се л, для e> 0 |
||||||||||||||||||||||||||||||||
сп раве дли во |
|
lim P( |
|
$(2) |
- θ |
|
< ε ) |
|
= 1, т.е . и ме е м состояте льную оце нк у. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
θ n |
|
|
|
|
|
|
||||||||||||||||||||||||||||
Рассмотри м е щ е одну оце нк у не и зве стног о мате мати ч е ск ог о ож и дани я:
θˆn(3) |
= |
x1 |
+ x2 + ... + xn |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
у к оторой |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(3) |
|
|
|
(Mξ1 |
|
|
|
+...+ Mξ n ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Mθ n |
= |
|
|
|
+ Mξ2 |
|
θ n = θ |
|
|
|
|
|
|
|
|
||||||||||||||||||
n |
n |
σ 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(3) |
|
|
|
1 |
|
(Dξ1 + Dξ2 +...+Dξn ) = |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Dθ n |
|
= |
|
|
|
nσ |
|
= |
|
n → 0 |
|
|
|
|
|
||||||||||||||||||
|
n2 |
n2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
п ри n®∞ , т.е . п осле дняяоце нк а так ж е |
не сме щ е ннаяи состояте льная. К ак ой |
ж е |
|||||||||||||||||||||||||||||||
оце нк е |
отдатьп ре дп оч те ни е ? Длятог о ч тобы отве ти тьна этот воп рос, сравни м |
||||||||||||||||||||||||||||||||
ди сп е рси и п осле дни хдвухоце нок . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
$(3) |
|
σ 2 |
|
|
$(2) |
|
2(2n +1) |
|
2 |
|
σ 2 |
æ |
n -1 |
ö |
|
|
|||||||||
П оск ольк у |
|
|
|
|
|
|
Dθ n |
= |
|
, Dθ n |
|
= |
|
|
|
|
|
σ |
|
= |
|
ç1 + |
|
|
÷ |
, |
то |
||||||
|
|
|
|
|
|
n |
|
3n(n |
+1) |
|
|
n |
|
|
|||||||||||||||||||
(2) |
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
3(n +1)ø |
|
|
|||||||||||
|
|
|
|
т.е . |
оце нк а |
ˆ |
(3) |
дае т ме ньши й |
|
разброс |
ок оло |
знач е ни й |
|||||||||||||||||||||
Dθ n |
> Dθ n |
, |
|
|
θn |
|
|
||||||||||||||||||||||||||
п араме тра q и , |
|
сле довате льно, |
п ре дп оч ти те льне е . В так ом случ ае |
г оворят, ч то |
|||||||||||||||||||||||||||||
оце нк а θˆn |
(3)эффект ивнее оце нк и |
θˆn |
(2). Т е п е рь е сте стве нно п остави ть воп рос о |
||||||||||||||||||||||||||||||
п острое ни и |
самой эффе к ти вной |
оце нк и – об оце нк е |
с ми ни мальной |
ди сп е рси е й . |
|||||||||||||||||||||||||||||
Т ак ая оце нк а назы вае тся эффект ивно й оце нк ой . |
Док азано, |
ч то эффе к ти вной |
|||||||||||||||||||||||||||||||
оце нк ой |
мате мати ч е ск ог о ож и дани я |
нормально |
расп ре де ле нной |
|
случ ай ной |
||||||||||||||||||||||||||||
