
Лабораторные работы по ТВиМС
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ве ли ч и ны |
|
являе тся оце нк а |
θˆn =(x1+x2+… |
+xn)/n. И ме нно п оэтому |
п осле дняя |
|||||||||||||||||||||||||||||||||||||||||||
оце нк а так |
ши рок о |
и сп ользуе тся в мате мати ч е ск ой |
стати сти к е . И так , |
вп ре дь |
||||||||||||||||||||||||||||||||||||||||||||
для |
оце нк и |
|
|
не и зве стног о |
|
|
мате мати ч е ск ог о |
ож и дани я случ ай ной |
|
|
ве ли ч и ны |
|||||||||||||||||||||||||||||||||||||
буде м и сп ользоватьвыбо ро ч но е с реднее, т. е : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
θˆn |
= x = |
x1+ + x2 |
+ ... + xn |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т оч еч ны еоценки д и спер си и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Для ди сп е рси и |
σ2 |
случ ай ной ве ли ч и ны ξ мож но п ре длож и ть сле дую щ ую |
|||||||||||||||||||||||||||||||||||||||||||
оце нк у: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
= |
1 |
n |
|
|
x −( x |
2 , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
DX |
|
|
|
|
x |
|
|
– вы бороч ное |
сре дне е , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
г де |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n åi =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Док азано, ч то эта оце нк а состояте льная, но с мещ енна я. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
В |
|
к ач е стве состояте льной |
не сме щ е нной |
оце нк и |
ди сп е рси и |
и сп ользую т |
|||||||||||||||||||||||||||||||||||||||
ве ли ч и ну |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
n |
|
|
|
|
2 |
|
|
|
1 |
|
æ |
|
n |
2 |
|
|
|
2 |
ö |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
s |
|
= |
|
|
|
|
|
|
å(xi - x) |
|
|
= |
|
|
|
|
ç |
åxi |
- nx |
|
÷. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
n -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
-1 i=1 |
|
|
|
|
|
|
|
è i=1 |
|
s2 |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
И ме нно |
|
не сме щ е нностью |
оце нк и |
|
объ ясняе тся е е |
|
|
боле е |
ч астое |
||||||||||||||||||||||||||||||||||||
и сп ользовани е |
|
в к ач е стве |
оце нк и ве ли ч и ны Dξ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
З аме ти м, ч то |
Mathcad п ре длаг ае т в к ач е стве |
|
оце нк и ди сп е рси и |
|
ве ли ч и ну |
||||||||||||||||||||||||||||||||||||||||
|
DX |
, а не s2: функ ци яvar(x) вы ч и сляе т ве ли ч и ну: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
1n åi=1 |
(xi − mean(x))2 |
, г де |
mean(x) - вы бороч ное |
сре дне е : |
|
åi=1 |
xi . |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
З АДАН И Е 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Най ди те |
состояте льны е |
не сме щ е нны е |
|
оце нк и мате мати ч е ск ог о |
|
ож и дани я |
|||||||||||||||||||||||||||||||||||||||
М ξ |
и |
|
ди сп е рси и |
|
Dξ |
случ ай ной |
ве ли ч и ны |
ξ |
|
п о |
п ри ве де нны м |
|
в задани и |
|||||||||||||||||||||||||||||||||||
вы бороч ны м знач е ни ям x1, x2, .., xn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
П ор я д ок вы полнени я |
зад ани я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1. |
П роч и тай те |
с |
ди ск а фай л, |
соде рж ащ и й |
|
вы бороч ны е |
|
знач е ни я, |
и ли |
||||||||||||||||||||||||||||||||||||
|
|
|
вве ди те |
|
заданную вы борк у с к лави атуры . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2. В |
ы ч и сли те |
точ е ч ны е |
|
оце нк и |
М ξ и |
Dξ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
П р и мер вы полнени я |
|
зад ани я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Най ди те |
состояте льны е |
не сме щ е нны е |
|
оце нк и мате мати ч е ск ог о |
|
ож и дани я |
|||||||||||||||||||||||||||||||||||||||
М ξ |
и |
|
ди сп е рси и |
|
Dξ |
случ ай ной |
|
ве ли ч и ны |
ξ |
п о |
вы бороч ны м |
знач е ни ям, |
||||||||||||||||||||||||||||||||||||
заданны м сле дующ е й табли це й . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
X |
904.3 |
|
|
910.2 |
916.6 |
928.8 |
|
|
935.0 |
|
941.2 |
|
947.4 |
|
953.6 |
|
959.8 |
966.0 |
|
972.2 |
978. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
N |
1 |
|
|
|
|
3 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|
1 |
|
|
1 |
1 |
|
|
|
2 |
|
1 |
||||||

|
22 |
|
Для вы борк и , |
заданной табли це й так ог о ти п а |
(п ри ве де но вы бороч ное |
знач е ни е и ч и сло, |
ук азы ваю щ е е , ск ольк о раз это |
знач е ни е встре ч ае тся в |
вы борк е ), формулы |
для состояте льны х не сме щ е нны х оце нок мате мати ч е ск ог о |
|
ож и дани яи ди сп е рси и и ме ю т ви д:
|
1 |
k |
1 |
k |
|||
x = |
åni xi , s2 = |
åni (xi |
|||||
|
n |
|
|||||
|
|
i=1 |
n − 1 i=1 |
||||
г де |
k |
– |
к оли ч е ство знач е ни й |
||||
вы борк е , n – |
объ е м вы борк и . |
||||||
n
− x)2 , n = åni ,
i=1
в табли це ; ni – к оли ч е ство знач е ни й xi в
Фраг ме нт рабоч е г о док уме нта Mathcad с вы ч и сле ни ями точ е ч ны хоце нок п ри ве де нни ж е . И зп ри ве де нны хвы ч и сле ни й ви дно, ч то сме щ е ннаяоце нк а дае т
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. М Е Т О ДЫ П О ЛУ Ч Е Н И Я Т О Ч Е Ч Н Ы Х О Ц Е Н О К |
|
|
|
|
|||||||||||||||||
И зве стны ме тоды п олуч е ни я точ е ч ны х оце нок : |
ме тод |
|
моме нтов, |
ме тод |
|||||||||||||||||||
мак си мальног о п равдоп одоби яи ме тод наи ме ньши хк вадратов. |
|
|
|
|
|||||||||||||||||||
О це нк и , п олуч е нны е |
ме тодом |
мак си мальног о |
|
|
п равдоп одоби я, обладаю т |
||||||||||||||||||
хороши ми |
а с импт о т ич ес кими |
свой ствами : |
п ри |
|
|
n®∞ |
|
они |
становятся |
||||||||||||||
эффе к ти вны ми , |
не сме щ е нны ми , |
состояте льны ми . |
|
|
П ознак оми мся с |
эти м |
|||||||||||||||||
ме тодом на п ри ме рах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.1 М |
етод макси мального пр авд опод оби я д ля д и скр етнойслуч айной |
||||||||||||||||||||||
П усть x – |
|
|
вели ч и ны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ди ск ре тная случ ай ная ве ли ч и на, |
расп ре де ле нная п о |
зак ону |
|||||||||||||||||||||
П уассона с не и зве стны м |
п араме тром |
l |
, т.е . |
P(ξ = m) = λm e−λ |
и m1, |
m2,.., mn – |
|||||||||||||||||
|
|
|
|
|
|
|
m! |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ре зультаты |
не зави си мы хнаблю де ни й случ ай ной |
ве ли ч и ны x. З адач а состои т в |
|||||||||||||||||||||
п острое ни и |
точ е ч ной |
оце нк и не и зве стног о п араме тра l. Дляе е ре ше ни явве де м |
|||||||||||||||||||||
в рассмотре ни е |
функцию пра вдо по до бия, заданную раве нством |
|
|
|
|
||||||||||||||||||
L(m1 ,m2 ,..,mn ) = p(ξ1 = m1 ,ξ2 = m2 ,..,ξn |
= mn ), |
|
|
|
|
||||||||||||||||||
г де x1, x2,.., xn - |
не зави си мы е случ ай ны е |
ве ли ч и ны , расп ре де ле нны е |
так ж е , к ак |
||||||||||||||||||||
и случ ай наяве ли ч и на x. |
|
|
|
|
|
|
|
|
|
|
|
= m ) = λmi e−λ |
|
|
|
|
|||||||
П оск ольк у случ ай ны е |
ве ли ч и ны x не зави си мы и |
P(ξ |
i |
, то |
|
||||||||||||||||||
|
|
|
|
i |
|
mi ! |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L(m ,m ,..,m ) = P(ξ |
= m )P(ξ |
|
= m )...P(ξ |
|
= m ) = |
λm1+...+mn |
e−nλ . |
||||||||||||||||
2 |
n |
|
|
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
1 |
2 |
n |
1 |
1 |
|
|
|
2 |
|
|
|
|
|
n |
m1 !..mn ! |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
К ак |
ви дно |
и з п осле дне г о раве нства, функ ци я п равдоп одоби я зави си т |
|||||||||||||||||||||
тольк о от ре зультатов наблюде ни й |
|
m1,m2,.., mn и |
от не и зве стног о п араме тра l. |
||||||||||||||||||||
З а оце нк у не и зве стног о п араме тра l п ри ме м так ое ч и сло мак си мум функ ци и п равдоп одоби я.
П ри ре ше ни и задач оты ск ани я мак си мума функ ци и все г о находят мак си мум функ ци и lnL:
, к оторое доставляе т
λ
п равдоп одоби я ч ащ е
æ |
λ |
mi +...+ mn |
ö |
|
|
|
|
|
||
ln L = lnç |
|
|
|
e− nλ ÷ = -nλ + (m |
+...+m ) ln λ - ln(m !... m !), |
|||||
|
|
|
|
|||||||
è m1 !...mn ! |
ø |
1+ |
|
n |
1 |
n |
||||
|
|
|
|
|
||||||
к оторая дости г ае т мак си мума в той ж е точ к е , |
ч то и |
функ ци я п равдоп одоби я |
||||||||
L(m1,m2,.. mn). |
|
|
|
|
|
|
|
|
|
|
И зне обходи мог о услови яэк стре мума |
|
|
|
|
||||||
∂ ln L |
= -n + |
m1 +...+m1 |
= 0 |
|
|
|
|
|||
∂λ |
|
|
|
|
|
|||||
|
|
|
|
λ |
|
|
|
|
|
|
1
име е м и ск омую оце нк у λ = n (m1,..., mn ) не и зве стног о п араме тра l.
|
|
24 |
|
|
|
|
|
|
|
|
В сп омни м, |
ч то |
мате мати ч е ск ое |
ож и дани е |
случ ай ной ве ли ч и ны |
ξ, |
|||||
и ме ю щ е й расп ре де ле ни е П уассона с п араме тром λ, равно |
М ξ |
= λ и |
ч то |
|||||||
эффе к ти вной , |
не сме щ е нной , состояте льной |
оце нк ой |
мате мати ч е ск ог о |
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
ож и дани яξ п о вы борк е m1,m2,.. mn являе тсяве ли ч и на m = |
|
|
|
|
= λ . |
|
||||
|
n(m1 |
+...+mn ) |
|
|||||||
|
|
|
|
|
|
|
|
|||
В Mathcad для моде ли ровани я вы борк и знач е ни й |
случ ай ной |
ве ли ч и ны , |
||||||||
расп ре де ле нной |
п о |
зак ону П уассона, |
п ре дназнач е на |
|
функ ци я |
rpois(k,λ)), |
||||
к отораяформи руе т ве к тор и зk случ ай ны хч и се л, расп ре де ле нны хп о П уассону с п араме тром λ.
З АДАН И Е 5 |
|
Смоде ли руй те не ск ольк о вы борок объ е ма п знач е ни й случ ай ной |
ве ли ч и ны |
ξ, и ме ю щ е й расп ре де ле ни е П уассона с п араме тром λ=0.1N, N – номе р вари анта. |
|
Дляодной вы борк и п острой те г рафи к функ ци и п равдоп одоби я. Най ди те оце нк у |
|
мак си мальног о п равдоп одоби я п араме тра λ к ак функ ци ю объ е ма |
вы борк и . |
В ы п олни те вы ч и сле ни ядляn = 10N, 20N,..., 50N п ри N < =15 и дляn = N, 2N,...,
10N п ри N > 15. И зобрази те |
на г рафи к е |
зави си мостьоце нк и от объ е ма вы борк и . |
|||||||||
Сравни те п олуч е нны е |
оце нк и с заданны м знач е ни е м п араме тра. |
|
|||||||||
П ор я д ок вы полнени я |
зад ани я |
|
|
|
|
|
|
||||
1. |
Смоде ли руй те |
вы борк у |
знач е ни й |
случ ай ной |
ве ли ч и ны , |
и ме ющ е й |
|||||
расп ре де ле ни е |
П уассона с заданны м знач е ни е м п араме тра λ. |
|
|||||||||
2. |
О п ре де ли те |
|
лог ари фм |
функ ци и |
мак си мальног о |
п равдоп одоби я и |
|||||
и зобрази те е г о г рафи к . |
|
|
|
|
|
|
|
|
|||
3. |
Смоде ли руй те |
не ск ольк о |
вы борок разног о объ е ма знач е ни й |
случ ай ной |
|||||||
ве ли ч и ны , и ме ю щ е й |
расп ре де ле ни е |
П уассона |
с |
заданны м |
знач е ни е м |
||||||
п араме тра λ. |
|
|
|
|
|
п равдоп одоби я п араме тра λ к ак |
|||||
4. |
В ы ч и сли те |
оце нк у |
мак си мальног о |
||||||||
функ ци ю объ е ма вы борк и . |
|
|
|
|
|
|
|
||||
5. |
И зобрази те |
на |
г рафи к е |
зави си мость |
оце нк и |
мак си мальног о |
|||||
п равдоп одоби яот объ е ма вы борк и . |
|
|
|
|
|
||||||
П р и мер вы полнени я зад ани я |
|
|
|
|
|
|
|||||
В |
п ри ве де нном |
ни ж е фраг ме нте |
рабоч е г о |
док уме нта |
вы п олне ны |
||||||
тре буе мы е вы ч и сле ни ядлярасп ре де ле ни яП уассона с п араме тром λ = 3.
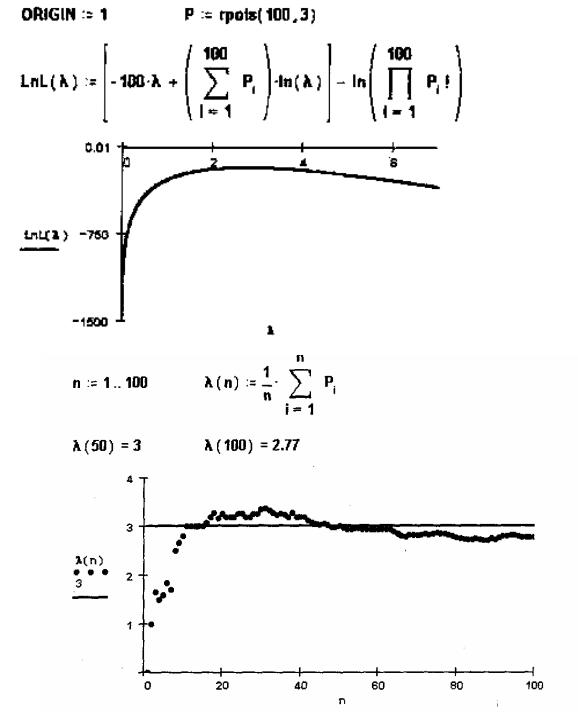
25
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
4.2 М |
етод макси мального пр авд опод оби я д ля непр ер ы внойслуч айной |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
вели ч и ны |
|
|
|
|
|
|
|
|
|||
П устьξ – случ ай наяве ли ч и на, расп ре де ле ннаяп о п ок азате льному зак ону с |
|||||||||||||||||||||
не и зве стны м п араме тром λ: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ì |
x < 0 |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Pξ (x) = í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
îλe−λx , x ³ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
З адач а состои т |
в |
п острое ни и |
ме тодом |
|
мак си мальног о |
п равдоп одоби я |
|||||||||||||||
оце нк и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ п араме тра λ п о вы бороч ны м знач е ни ям x1,x2,..,xn. |
|
|
|
||||||||||||||||||
П о аналог и и |
с п ре ды дущ и м разде лом оп ре де ли м функ ци ю п равдоп одоби я |
||||||||||||||||||||
раве нством |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L(x1, x2 ,.., xn ) = ∏ pξ (xi ) = λne−λ( x1 +...+ xn ) . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
К ак ви дно, |
функ ци я п равдоп одоби я зави си т не |
|
тольк о |
от вы бороч ны х |
|||||||||||||||||
знач е ни й , |
но и от не и зве стног о п араме тра расп ре де ле ни я λ. |
К ак |
и |
вы ше , за |
|||||||||||||||||
оце нк у не и зве стног о |
п араме тра λ п ри ме м так ое ч и сло |
|
|
доставляе т |
|||||||||||||||||
λ , к оторое |
|||||||||||||||||||||
мак си мум |
функ ци и |
п равдоп одоби я. |
Снова п е ре ходи м |
к лог ари фму функ ци и |
|||||||||||||||||
п равдоп одоби я, |
п ри ме няе м |
не обходи мое |
услови е |
|
эк стре мума |
|
и п осле |
||||||||||||||
не слож ны хвы ч и сле ни й |
п олуч ае м: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ln L = nln λ − (x + ... + x )λ, |
∂ ln L |
= |
n |
− (x + ... + x ) = 0 |
|||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
n |
|
∂λ |
|
λ |
1 |
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ˆ |
|
|
n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ = |
|
|
= |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
x + ... + x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ч то е сте стве нно, |
п оск ольк у |
мате мати ч е ск ое |
ож и дани е |
случ ай ной |
|
ве ли ч и ны , |
|||||||||||||||
и ме ю щ е й |
п ок азате льное |
расп ре де ле ни е с п араме тром λ, равно 1/λ. |
|
|
|||||||||||||||||
В |
Mathcad для моде ли ровани я вы борк и |
знач е ни й |
случ ай ной |
|
ве ли ч и ны , |
||||||||||||||||
и ме ю щ е й |
п ок азате льное |
расп ре де ле ни е , п ре дназнач е на функ ци я |
rexp(k,λ), |
||||||||||||||||||
к отораяформи руе т ве к тор и зk случ ай ны хч и се л, расп ре де ле нны хп ок азате льно с п араме тром λ.
|
З АДАН И Е 6 |
|
|
|
|
|
|
|
Смоде ли руй те не ск ольк о вы борок объ е ма n знач е ни й |
случ ай ной |
ве ли ч и ны |
||||
ξ, и ме ю щ е й п ок азате льное расп ре де ле ни е с п араме тром |
λ == 0.1N, г де N – |
||||||
номе р вари анта. |
Для |
одной |
вы борк и |
п острой те |
г рафи к |
функ ци и |
|
п равдоп одоби я. Най ди те |
оце нк у мак си мальног о п равдоп одоби я п араме тра λ |
||||||
к ак |
функ ци ю объ е ма вы борк и . В ы п олни те вы ч и сле ни ядляn = 10N, 20N,.... 50N |
||||||
п ри |
N < =15 и для n = N, 2N,..., 10N п ри |
N > 15. И зобрази те на г рафи к е |
|||||
зави си мость оце нк и |
от |
объ е ма |
вы борк и . |
Сравни те п олуч е нны е |
оце нк и с |
||
заданны м знач е ни е м п араме тра. |
|
|
|
|
|||
|
|
|
|
|
|
|
27 |
|
|
|
П ор я д ок вы полнени я |
зад ани я |
|
|
|
|
|||||
1. |
Смоде ли руй те |
вы борк у |
знач е ни й |
случ ай ной ве ли ч и ны , |
и ме ющ е й |
|||||
эк сп оне нци альное |
расп ре де ле ни е |
с заданны м знач е ни е м п араме тра λ. |
||||||||
2. |
О п ре де ли те |
лог ари фм |
функ ци и |
мак си мальног о п равдоп одоби я и |
||||||
и зобрази те |
е г о г рафи к . |
|
|
|
|
|
|
|||
3. |
Смоде ли руй те |
не ск ольк о |
вы борок разног о объ е ма знач е ни й |
случ ай ной |
||||||
ве ли ч и ны , |
и ме ю щ е й |
эк сп оне нци альное расп ре де ле ни е |
с |
заданны м |
||||||
знач е ни е м п араме тра λ. |
|
|
п равдоп одоби я п араме тра λ к ак |
|||||||
4. |
В ы ч и сли те |
оце нк у |
мак си мальног о |
|||||||
функ ци ю объ е ма вы борк и . |
|
|
|
|
|
|||||
5. |
И зобрази те |
|
на |
г рафи к е |
зави си мость оце нк и |
мак си мальног о |
||||
п равдоп одоби яот объ е ма вы борк и . |
|
|
|
|||||||
П р и мер вы полнени я зад ани я |
|
|
|
|
||||||
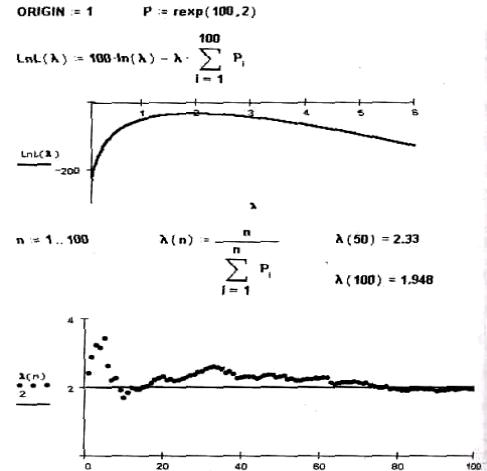
В п ри ве де нном ни ж е |
фраг ме нте |
рабоч е г о док уме нта вы п олне ны тре буе мы е |
||||||||
вы ч и сле ни ядляэк сп оне нци альног о расп ре де ле ни яс п араме тром λ=2.
|
28 |
|
|
|
5. П РО В Е РКА С Т АТ И С Т И Ч Е С КИ Х ГИ П О Т Е З О П АРАМ |
Е Т РАХ |
|||
Н О РМ АЛЬ Н О РАС П РЕ ДЕ ЛЕ Н Н О Й С ЛУ Ч АЙ Н О Й В Е ЛИ Ч И Н Ы |
||||
|
|
|
вы борк е |
и з случ ай ной |
П усть дана не к оторая оце нк а θ , п острое нная п о |
||||
ве ли ч и ны ξ. |
Е сть основани я сч и тать, |
ч то и сти нное |
знач е ни е |
оце ни вае мог о |
п араме тра равно θ0. О днак о вы бороч ное |
|
|
|
|
знач е ни е θ вряд ли буде т совп адатьс |
||||
θ0, п оск ольк у |
|
В связи с эти м возни к ае т воп рос, п ри |
||
θ – случ ай ная ве ли ч и на. |
||||
|
|
|
|
|
к ак ом отк лоне ни и θ от θ0 и с к ак ой сте п е нью уве ре нности мож но утве рж дать, |
||||
ч то и сти нное |
|
|
|
|
знач е ни е оце ни вае мог о п араме тра θ отли ч но от θ0. О тве том на |
||||
этот воп рос мож е т служ и тьве роятность(вы ч и сле ннаяв п ре дп олож е ни и θ = θ0 )
тог о, ч то |
|
θ0 больше не к оторог о фи к си рованног о ч и сла, о ве ли ч и не к оторог о |
||||||||||||||||||||
θ - |
||||||||||||||||||||||
буде т ск азано ни ж е . Е сли |
эта ве роятность мала, то мы являе мся сви де те лями |
|||||||||||||||||||||
малове роятног о |
собы ти я, |
|
т.е . |
|
отли ч и е |
эмпирич ес ко го |
знач е ни я |
|
от |
|||||||||||||
|
|
θ |
||||||||||||||||||||
гипо т ет ич ес ко го |
знач е ни яθ0 п ре дставляе тсязна ч имым, и |
г и п оте за о том, ч то θ |
||||||||||||||||||||
= θ0 , долж на бы тьотве рг нута. Е сли |
ж е |
эта ве роятность ве ли к а, то отк лоне ни е |
||||||||||||||||||||
|
от |
θ0, |
п о-ви ди мому, |
обусловле но |
е сте стве нной |
случ ай ностью , |
и , |
|||||||||||||||
θ |
||||||||||||||||||||||
сле довате льно, г и п оте за о том, ч то |
|
= θ0, мож е т бы тьп ри нята. |
|
|
|
|
|
|||||||||||||||
θ |
|
|
|
|
|
|||||||||||||||||
|
Наша задач а состои т в вы работк е |
общ е г о п одхода к |
п роце дуре , к оторая |
|||||||||||||||||||
назы вае тся п рове рк ой |
|
|
|
|
|
|
– вы бороч ное знач е ни е |
оце ни вае мог о |
||||||||||||||
г и п оте з. П усть θ |
||||||||||||||||||||||
п араме тра θ и п усть |
p – п лотность ве роятносте й случ ай ной |
ве ли ч и ны |
|
п ри |
||||||||||||||||||
θ |
||||||||||||||||||||||
|
|
|
θ = |
θ |
|
θ |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
услови и , |
ч то |
0 |
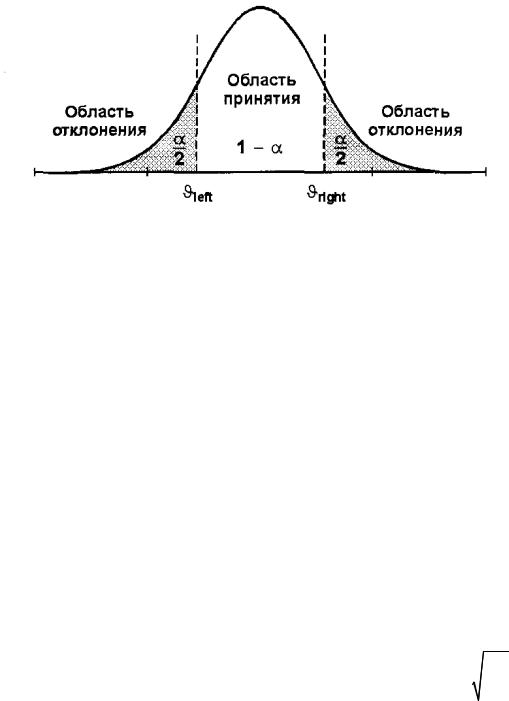
На ри с. 1 |
и зображ е н г рафи к |
функ ци и |
|
|
, на к отором |
||||||||||||||
отме ч е ны точ к и θleft и |
θright |
, |
дляк оторы хвы п олне ны |
услови я: |
θ |
|
) = 0.5α , |
|||||||||||||||
P(θ ≤ θ left |
||||||||||||||||||||||
|
|
|
|
г де |
α – |
не к оторое |
малое |
ч и сло. |
Это ч и сло |
и ме е т п ростой |
||||||||||||
P(θ > θ right ) = 0.5α , |
||||||||||||||||||||||
смы сл: е сли |
ве роятность собы ти я не |
п ре вы шае т α, |
то собы ти е |
малове роятно, |
||||||||||||||||||
т.е . е сли |
вы ч и сле нное |
|
|
|
ок аж е тсявне |
п роме ж утк а (θleft , θright ), то е сть |
||||||||||||||||
знач е ни е θ |
|
|||||||||||||||||||||
все |
основани яусомни тьсяв том, |
ч то и сти нное |
знач е ни е п араме тра θ равно θ0, и |
|||||||||||||||||||
в этом случ ае |
г и п оте зу о том, ч то θ = θ0 , сле дуе т отве рг нуть(отк лони ть). Е сли |
|||||||||||||||||||||
ж е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ п оп адае т в и нте рвал(θleft , θright ), то г и п оте за о том, ч то θ = θ0 , мож е т бы ть |
||||||||||||||||||||||
п ри нята. В е роятностьα, и сп ользованнаяп ри вы ч и сле ни и и нте рвала (θleft , θright),
назы вае тся уро внем зна чимо с т и; |
области |
знач е ни й |
|
|
к оторы х г и п оте за |
|||
θ , п ри |
||||||||
отве рг ае тся и ли |
п ри ни мае тся, |
назы ваю тся соотве тстве нно |
о бла с т ью |
|||||
о т кло нения(крит ич ес ко йо бла с т ью) и о бла с т ью принят иягипо т езы. |
||||||||
В |
п ри ве де нном |
на ри с. 1 п ри ме ре |
к ри те ри й |
п рове рк и г и п оте зы бы л |
||||
двус т о ро нним, п оск ольк у знач и мы ми бы ли |
|
|
от |
θ0 в обе |
стороны . |
|||
отк лоне ни я θ |
||||||||
Е сли |
отк лоне ни я знач и мы тольк о |
|
|
|
θ0 |
|
< θ0), то |
|
в одну сторону (θ > |
и ли θ |
|||||||
строятсяо дно с т о ро нние крит ерии.
29
|
Ри с. 1. О бласти п ри няти яи отк лоне ни яги п оте з |
|
|
|
||||||
Сле дуе т обрати ть вни мани е |
на то, ч то в рассматри вае мы х нами |
задач ах |
||||||||
п ри няти е |
и ли |
отк лоне ни е |
г и п оте зы |
не носят к ате г ори ч е ск ог о |
харак те ра. |
|||||
Ре ше ни е |
об отк лоне ни и и ли |
п ри няти и |
г и п оте зы мож е т ок азаться оши боч ны м: |
|||||||
г и п оте за отк лоняе тся, хотя она на самом де ле |
ве рна (оши бк а перво го |
ро да ), и |
||||||||
г и п оте за п ри ни мае тся, хотяона на самом де ле не ве рна (оши бк а вт о ро го |
ро да ). |
|||||||||
5.1 |
П р овер ка |
ги потезы |
о ч и словом |
знач ени и |
математи ч еского |
|||||
ож и д ани я пр и |
и звестнойд и спер си и |
|
|
|
|
|
||||
П усть М ξ = a – |
не и зве стная ве ли ч и на, а ди сп е рси я Dξ = σ2 и зве стна. |
|||||||||
Сформули руе м нуле вую г и п оте зу |
H0 о том, ч то не и зве стны й п араме тр а раве н |
|||||||||
заданному ч и слу a0 |
, т.е . H0: a=a0. |
Альте рнати вную |
г и п оте зу |
H1 |
мож но |
|||||
сформули роватьтре мясп особами : |
|
|
|
|
|
|||||
1)H1: a ¹ a0;
2)H1: a > a0;
3)H1: a < a0.
Рассмотри м п одробно к аж ды й и зэти хтре хслуч ае в.
О брати мся к п е рвому случ аю : нуле вая г и п оте за H0: a = a0 и альте рнати внаяг и п оте за H1: a ¹ a0 . З адади мсяне к оторы м уровне м знач и мости
α и вы ч и сли м п о вы борк е |
x = (x1, x2 ,.., xn ) |
знач е ни е к ри те ри яϕ = |
x |
− a0 |
. |
||||
|
|
|
|||||||
σ 2 |
|||||||||
|
|
|
|
|
|
||||
Е сли г и п оте за H0 ве рна, то случ ай ная ве ли ч и на j и ме е т |
|
n |
|||||||
стандартное |
|||||||||
нормальное расп ре де ле ни е , и |
здравы й смы сл п одск азы вае т, ч то в больши нстве |
||||||||
эк сп е ри ме нтов ве ли ч и на |
j |
буде т мало |
отли ч аться от нуля. |
Е сли ж е е е |
|||||
отк лоне ни я от нуля ве ли к и , то это, ск оре е все г о, ук азы вае т на оши боч ность г и п оте зы H0. П ри дади м п ри ве де нны м соображ е ни ям боле е ч е тк ую форму.
В ы де ли м для к ри те ри я j – крит ич ес кую о бла с т ь, т.е . ук аж е м так и е знач е ни яj, п ри к оторы хг и п оте зу H0 сле дуе т отве рг нуть. На ри с. 2 и зображ е на п лотность расп ре де ле ни я к ри те ри я j (п лотность стандартног о нормальног о расп ре де ле ни я).

30
|
|
Ри с. 2. К ри ти ч е ск аяобластьдляальте рнати вной |
г и п оте зы H1 :a¹a0 |
|
||||||||||||||||||||
О п ре де ли м г рани цы к ри ти ч е ск ой области |
xl,α и |
xr,α |
так , ч тобы |
|
|
|||||||||||||||||||
|
P(ϕ < xl,α ) = |
α , P(ϕ > xr,α ) = |
α . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
К ри ти ч е ск и е |
точ к и xl,α и xr,α расп олож е ны |
си мме три ч но |
относи те льно |
||||||||||||||||||||
нуля, п раваяявляе тсяк орне м уравне ни яФ(x |
)= 1 — |
0.5α, а ле ваявы ч и сляе тся |
||||||||||||||||||||||
п о формуле xl,α = - xr,α. |
|
|
|
|
|
|
|
r,α |
|
|
|
|
|
|
|
|||||||||
|
область |
най де на, |
мож но |
вы ч и сли ть |
п о |
вы борк е |
||||||||||||||||||
|
К ог да |
к ри ти ч е ск ая |
||||||||||||||||||||||
знач е ни е к ри те ри яj и п рове ри ть, п оп адае т ли оно в к ри ти ч е ск ую область. |
||||||||||||||||||||||||
|
Е сли |
ϕ< xl,α |
и ли |
ϕ> xr,α, то |
г и п оте за |
|
H0 |
отве рг ае тся и |
п ри ни мае тся |
|||||||||||||||
г и п оте за H1. Е сли |
ж е xl,α<ϕ<xr,α то п ри ни мае тсяг и п оте за H0. |
|
соде рж ащ и й |
|||||||||||||||||||||
|
Ни ж е |
п ри ве де н |
фраг ме нт рабоч е г о |
док уме нта |
Mathcad, |
|||||||||||||||||||
п рове рк у |
г и п оте зы |
о |
ве ли ч и не |
|
|
мате мати ч е ск ог о |
ож и дани я нормально |
|||||||||||||||||
расп ре де ле нной |
случ ай ной |
ве ли ч и ны |
H0: а |
|
= 1 п ри |
альте рнати вной |
ги п оте зе |
|||||||||||||||||
H1: а |
¹ 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H0: |
а |
= a0 и |
||
|
Рассмотри м |
|
второй |
|
случ ай |
с |
нуле вой |
г и п оте зой |
||||||||||||||||
альте рнати вной |
ги п оте зой |
|
H1: а > a0. Снова задади мся не к оторы м |
уровне м |
||||||||||||||||||||
знач и мости α и |
вы ч и сли м |
п о вы борк е |
|
= (x1, x2 ,.., xn ) |
знач е ни е |
к ри те ри я |
||||||||||||||||||
x |
||||||||||||||||||||||||
|
x − a |
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
||||
j = |
|
|
0 |
|
, |
|
|
г де |
|
x = |
|
åxi . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
s |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
|
|
|
|||
n
