Коэффициенты метода определяются из условия корректности (24). В этом случае (24) примет вид

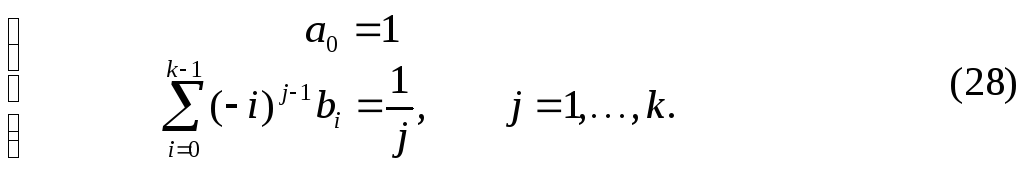
Определитель этой системы отличен от нуля и, следовательно, существует единственное решение. Таким образом, для любого решение системы (28) однозначно определяет метод Адамса-Башфорта порядка(метод является состоятельным).

Таблица 1. Алгоритмы метода Адамса-Башфорта.

Порядок	Алгоритм
Первый	(явный метод Эйлера)
Второй
Третий
Четвертый

Для численной реализации метода Адамса-Башфорта порядка требуетсястартовых значений(метод является- шаговым).

Метод Адамса-Мултона (интерполяционный метод Адамса).

Метод Адамса-Мултона порядка является неявным многошаговым методом полиномиальной аппроксимации, полученным из (22) при условии

то есть

Коэффициенты метода определяются из условия корректности (24). В этом случае (24) примет вид

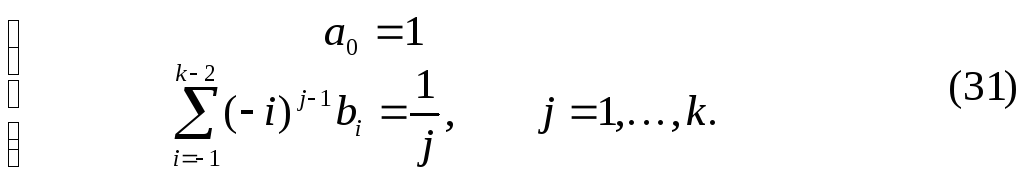
Определитель этой системы отличен от нуля и, следовательно, существует единственное решение. Таким образом, для любого решение системы (31) однозначно определяет метод Адамса-Мултона порядка(метод является состоятельным).

Для численной реализации метода Адамса-Мултона порядка требуетсястартовых значений(метод является- шаговым).

Таблица 2. Алгоритмы метода Адамса-Мултона.

Порядок	Алгоритм
Первый	(неявный метод Эйлера)
Второй	(метод трапеций)
Третий
Четвертый

Связь неявных методов с методами прогноза-коррекции.

Запишем алгоритм (22) неявногомногошагового метода полиномиальной аппроксимации в виде

Для определения единственной неизвестной величины получаем из (32) уравнение

где

Пусть удовлетворяет условию Липшица с константойпридля всех,, где- точное решение уравнения (33). При выполнении условия

функция в (33) является сжимающим отображением и, следовательно, при любом выборе начального приближенияитерационный процесс

при сходится к точному решениюуравнения (33).

Отметим, что скорость сходимости (35) становится медленной, если величина будет близка к 1. Поэтому для увеличения скорости сходимости придется выбирать малый шаг. Но это приведет к увеличению числа шагови ошибок округления. В качестве компромисса предлагается «хорошо» выбирать начальное приближение. Пусть, например, решение задачи (1) находится методом Адамса-Мултона четвертого порядка. Для предсказанияможно выбрать явный метод Эйлера (7) (прогноз)

и полученное значение использовать в качестве начального приближения итерационного процесса (35) (коррекция)

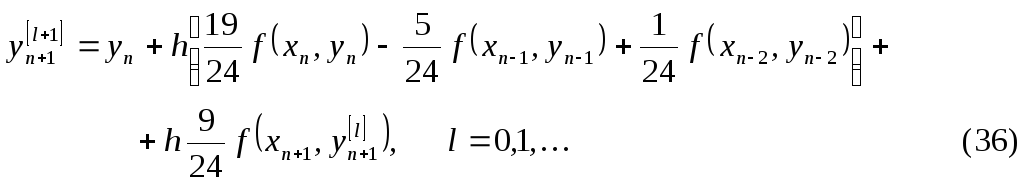
Формула (36) дает скорректированное значение послеитераций. Число итерацийзависит от желаемой точности решения и локальной алгоритмической ошибки прогноза. Если для прогноза выбрать более точный метод

то для требуемой точности ответа обычно достаточно одной итерации .

Замечания.

1) Многошаговый метод не являетсясамоначинающимся (самостартующим) в отличие от одношагового метода. Для реализации многошагового метода полиномиальной аппроксимации (22) нужно задатьпредыдущих (стартовых) значений. Очевидно, что для получения этих значений должен быть использован по крайней мерераз одношаговый метод. Обычно для вычисления стартовых значений пользуются методом Рунге-Кутта.

2) При численной реализации некоторых алгоритмов методов полиномиальной аппроксимации алгоритмическая ошибка и ошибка округления могут усиливаться (накапливаться) при каждом шаге. Поэтому через несколько шагов возросшая ошибка будет преобладать над самим решением. Это делает совершенно бесполезным применение таких методов. Таким образом, метод должен быть не только точным, но и устойчивым в том смысле, что алгоритмическая ошибка и ошибка округления должны оставаться ограниченными при достаточно малой величине шага при.

Устойчивость методов полиномиальной аппроксимации.

При анализе устойчивости метода полиномиальной аппроксимации обычно обращаются к тестовой задаче Коши

где - комплексный параметр.

Применим алгоритм (22) к решению задач (38), получим

Преобразуем (39) в эквивалентное разностное уравнение

где .

Положив в (40) , получим после сокращения намногочлен степени:

Многочлен (41) будем называть характеристическим многочленомметода полиномиальной аппроксимации (22).

Общее решение разностного уравнения (40) определяется выражением

где -различных корней характеристического многочлена (41),- произвольные постоянные, значения которых находятся из стартовых значенийрешения. Если характеристический многочлен (41) имеет кратный корень(- его кратность), то соответствующее слагаемое в формуле (42) общего решения будет иметь вид

Заметим, что если , топри(даже в том случае, когда корень- простой). Если- корень кратностии, то из (43) следует, чтопри.

Замечание. Призначениеявляется простым корнем характеристического многочленатогда и только тогда, когда.

Теорема (критерий устойчивости методов полиномиальной аппроксимации).

Состоятельный метод полиномиальной аппроксимации (22), удовлетворяющий условию , устойчив(в том смысле, что локальная алгоритмическая ошибка метода и ошибка округления остаются ограниченными при достаточно малой величине шага )тогда и только тогда, когда все корнимногочлена

таковы, что , а те корни, для которых, простые.

Корни многочлена (44) принято называть паразитными.

Замечание. Методы Адамса-Башфорта и Адамса-Мултона устойчивые. Действительно, для этих методов,. Поэтому

.

Здесь все корни многочлена равны нулю и, следовательно, лежат внутри единичного круга.

Обозначим через - решение уравнения

со стартовыми значениями ().

Теорема(оценка глобальной погрешности многошагового метода полиномиальной аппроксимации).

Пусть выполнены следующие условия:

1. Правая часть дифференциального уравнения определена непрерывна в областии существует константа, не зависящая оттакая, что в области

2. Пусть- точное решение уравнения задачи Коши (1) имеет на отрезкенепрерывные производные до порядка,.

3. Метод полиномиальной аппроксимации (22) является состоятельным и .

4. При достаточно малом все корнимногочлена

таковы, что , а те корни, для которых, простые.

Тогда для глобальной ошибки метода (22) справедлива оценка

где ,,-локальная ошибка округления на-ом шаге,- постоянные, зависящие от коэффициентов формулы (22) и правой части дифференциального уравненияи независящие от,.

Из (45) следует, что глобальная ошибка метода полиномиальной аппроксимации состоит из трех частей:

1. ошибка при вычислении стартовых значений,

2) суммарная алгоритмическая ошибка метода, характеризуемая величиной , убывающая с уменьшением,

3) ошибка округления, представленная членом , который растет с уменьшением.

Погрешность, очевидно, растет с увеличением длины отрезка, на котором разыскивается решение.

Замечание. Все описанные методы решения задачи Коши (1) переносятся на системы дифференциальных уравнений

где

или

…….

Формулы сохраняются в прежнем виде, нужно только заменить на,на. В оценках погрешности абсолютная величина заменяется на норму вектора.

6. Задание. Найдите на отрезкерешение задачи Коши для системы обыкновенных дифференциальных уравнений

с точностью , методами Рунге-Кутта, Адамса-Башфорта четвертого порядка и прогноза-коррекции (используя для прогноза алгоритм (37) и коррекции – метод Адамса-Мултона четвертого порядка).

Варианты заданий.

№ варианта
1				0,5	1,5
2				-1	1
3				1	1
4				0	0
5				0	0
6				0,5	1,2
7				0	0
8				-1	1
9				1	1
10				0,7	-0,5
11				0	0
12				0,2	0
13				1	-1
14				0	0
№ варианта
15				-1	2
16				0	1/6
17				0	1/7
18				0	0,125
19				0	1/9
20				0	0,1
21				0	1/11
22				0	1/11
23				0	1/12
24				0	1/13
25				0	1/14
26				0	1/6
27				0	1/7
28				0	0,125
29				0	1/9
30				0	0,1
31				0	1/11
32				0	1/12

Приложение. Для выполнения задания можно использовать следующие процедуры (на языке Паскаль):

1) Процедура rung, реализующая алгоритм метода Рунге-Кутта четвертого порядка (18):

Procedure rung(h:real; var x0:real;var y0:vector; n:integer);

{Входные параметры:

h – шаг интегрирования системы;

x0 – стартовое значение аргумента;

y0 – массив, содержащий значения решения системы в точке x0;

n - размерность системы.

Выходные параметры:

y0 – массив, содержащий значения решения системы в точке x0+h.

Здесь vector - одномерный массив порядка n}

var

i:integer;

begin

f(x0,y0,k1); for i:=1 to n do yt[i]:=y0[i]+0.5*h*k1[i];

f(x0+0.5*h,yt,k2); for i:=1 to n do yt[i]:=y0[i]+0.5*h*k2[i];

f(x0+0.5*h,yt,k3); for i:=1 to n do yt[i]:=y0[i]+h*k3[i];

f(x0+h,yt,k4); x0:=x0+h;

for i:=1 to n do y0[i]:=y0[i]+(h/6)*(k1[i]+2*k2[i]+2*k3[i]+k4[i])

end;

2) Процедура ad , реализующая алгоритм метода Адамса-Башфорта четвертого порядка (см. Таблицу 1):

Procedure ad(h:real;var yt:start;var y0:vector);

{Входные параметры:

h – шаг интегрирования системы;

yt – двумерный массив порядка (n,4)(n-размерность системы),столбцы

которого являются решениями системы в четырех стартовых точках.

Выходные параметры:

y0 – массив, содержащий решение системы в точке, отстоящей на 4h от

первой стартовой.

Здесь start – двумерный массив порядка (n,4), vector - одномерный

массив порядка n, kof – одномерный массив порядка 4.}

var

i,j:integer; kf:kof;

begin

kf[1]:=-9.0/z; kf[2]:=37.0/z; kf[3]:=-59.0/z; kf[4]:=55.0/z;

for i:=1 to n do

for j:=1 to 4 do

y0[i]:=y0[i]+h*yt[j,i]*kf[j]

end;

3) Процедура ad_mult, реализующая алгоритм метода прогноза-коррекции: прогноз - явный метод (37), коррекция - метод Адамса-Мултона четвертого порядка (см. Таблицу 2).

Procedure ad_mult(x0,h,eps:real;ys:start;var yc:vector);

{ {Входные параметры:

x0 – первая стартовая точка решения системы;

h - шаг интегрирования системы;

eps- значение в условии окончания итерационного процесса при

коррекции решения ;

ys – двумерный массив порядка (n,3) (n-размерность системы),

столбцами которого являются решения системы в трех стартовых

точках.

Выходные параметры:

yc - массив, содержащий решение системы в точке, отстоящей на 3h от

первой стартовой.

Здесь start – двумерный массив порядка (n,3), vector - одномерный

массив порядка n, kof – одномерный массив порядка 4.}

var

i,j :word;

yt :start; {

yp,y :vector; {

ka_m :kof;

x :real;

begin

yp:=ys[3];

for j:=1 to 3 do f(x0+j*h,ys[j+1],yt[j]);

ka_m[1]:=1/z; ka_m[2]:=-5/z; ka_m[3]:=19/z; ka_m[4]:=9/z;

for i:=1 to n do yp[i]:=yp[i]+2*h*yt[3,i]; {прогноз}

f(x0+4*h,yp,yt[4]);

yc:=ys[4];

for i:=1 to n do

for j:=1 to 4 do

yc[i]:=yc[i]+h*yt[j,i]*ka_m[j];

while nr(yp,yc)>=eps do

{nr – имя функции,вычисляющей норму разности двух векторов}

begin yp:=yc; y:=ys[4];

f(x0+4*h,yc,yt[4]);

for i:=1 to n do

for j:=1 to 4 do

y[i]:=y[i]+h*yt[j,i]*ka_m[j];

yc:=y

end

end;

function nr(z,z1:vector):real;

{vector - одномерный массив порядка n}

var i :word;

q :real;

begin

q:=0; for i:=1 to n do

if abs(z1[i]-z[i])>=q then q:=abs(z1[i]-z[i]);

nr:=q

end;

Составитель – Трофимов Валерий Павлович

Редактор - Бунина Т.Д.

19