
- •Министерство образования Российской Федерации
- •Из формулы (6) при получаем
- •3. Метод Рунге-Кутта.
- •4. Общий одношаговый метод.
- •4. Методы полиномиальной аппроксимации.
- •Коэффициенты метода определяются из условия корректности (24). В этом случае (24) примет вид
- •Коэффициенты метода определяются из условия корректности (24). В этом случае (24) примет вид
Из формулы (6) при получаем
![]()
Этот
алгоритм называется явным
методом Эйлера. Здесь
![]() .
.
Метод Тейлора второго порядка.
При
![]() из формулы (6) получаем
из формулы (6) получаем
![]()
где
![]()
3. Метод Рунге-Кутта.
Метод
Рунге-Кутта имеет тот же порядок точности,
что и метод Тейлора, но исключает
необходимость вычисления значений
частных производных от правой части
дифференциального уравнения
![]() .
Основная идея метода состоит в замене
функции
.
Основная идея метода состоит в замене
функции![]() в формуле (6) другой функцией
в формуле (6) другой функцией![]() ,
не требующей вычисления частных
производных от
,
не требующей вычисления частных
производных от![]() и удовлетворяющей условию
и удовлетворяющей условию
![]()
где
![]() -
константа, не зависящая от
-
константа, не зависящая от![]() .
Таким образом, алгоритм метода Рунге-Кутта
имеет вид:
.
Таким образом, алгоритм метода Рунге-Кутта
имеет вид:
![]()
где
![]() удовлетворяет условию (9). Очевидно,
метод (10) имеет ту же алгоритмическую
ошибку, что и метод Тейлора. Алгоритм
(10) принято называтьметодом Рунге-Кутта
порядка
удовлетворяет условию (9). Очевидно,
метод (10) имеет ту же алгоритмическую
ошибку, что и метод Тейлора. Алгоритм
(10) принято называтьметодом Рунге-Кутта
порядка
![]() .
.
Функцию![]() разыскивают в виде:
разыскивают в виде:![]()
![]()
где
![]()
![]()
![]()
![]()
![]()
В формулах (11)
коэффициенты
![]() и
и![]() находятся из условия (9).
находятся из условия (9).
Метод Рунге-Кутта первого порядка.
При
![]() получаем из (11)
получаем из (11)
![]()
Сравнивая
![]() с
с![]() ,
немедленно получаем из условия (9), что
,
немедленно получаем из условия (9), что![]() .
Таким образом метод Рунге-Кутта первого
порядка совпадает с явным методом
Эйлера:
.
Таким образом метод Рунге-Кутта первого
порядка совпадает с явным методом
Эйлера:
![]()
Метод Рунге-Кутта второго порядка.
При
![]() получаем из (11)
получаем из (11)
![]()
Разлагая
![]() во втором слагаемом в (12) по формуле
Тейлора в точке
во втором слагаемом в (12) по формуле
Тейлора в точке![]() получаем
получаем
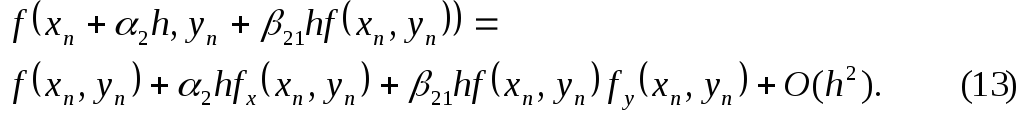
Подставляя (13) в (12), имеем
![]()
С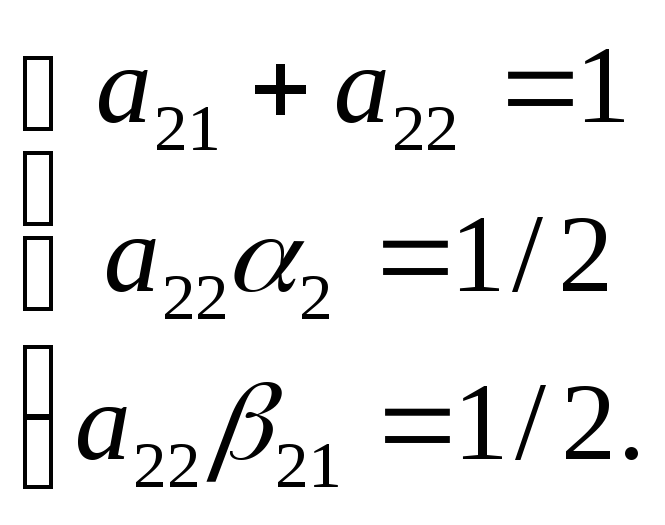 равнивая
равнивая![]() и (14), получаем из условия (9) нелинейную
систему уравнений для определения
коэффициентов
и (14), получаем из условия (9) нелинейную
систему уравнений для определения
коэффициентов![]() :
:
Отсюда следует,
что для различных
![]() существует целое семейство методов
Рунге-Кутта второго порядка с
коэффициентами
существует целое семейство методов
Рунге-Кутта второго порядка с
коэффициентами![]() и
и
![]() :
:
![]()
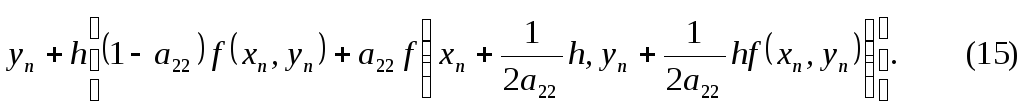
Приведем примеры алгоритмов метода Рунге-Кутта второго порядка.
Метод Хьюна (модифицированный метод трапеций).
В этом случае ![]() ,
,![]()
![]() Из
(15) получаем алгоритм метода Хьюна
Из
(15) получаем алгоритм метода Хьюна
![]()
Модифицированный метод Эйлера.
В этом случае ![]() ,
,![]()
![]() Из
(15) получаем алгоритм модифицированного
метода Эйлера
Из
(15) получаем алгоритм модифицированного
метода Эйлера
![]()
Метод Рунге-Кутта четвертого порядка.
Наиболее часто в вычислительной практике используется метод Рунге-Кутта четвертого порядка, алгоритм которого определяется формулами
![]()
где
![]()
![]()
![]()
![]()
![]()
Отметим,
что если правая часть дифференциального
уравнения
![]() не зависит от
не зависит от![]() ,
то формула (18) совпадает с квадратурной
формулой Симпсона. (Решение задачи Коши
,
то формула (18) совпадает с квадратурной
формулой Симпсона. (Решение задачи Коши![]() равносильно вычислению интеграла
равносильно вычислению интеграла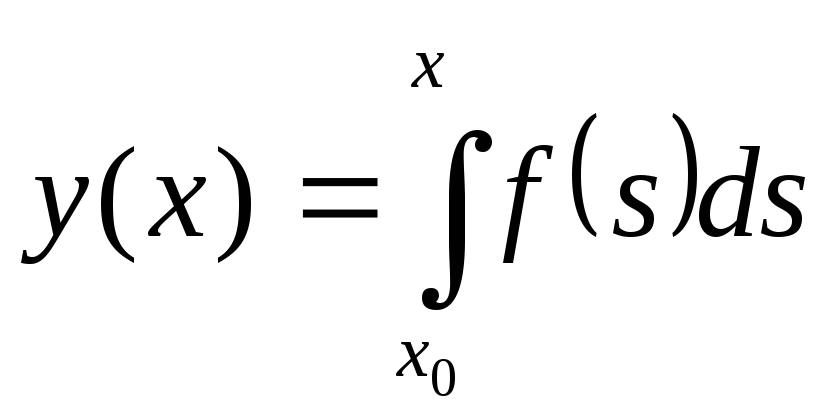 ).
).
Замечание.
Метод (18) часто называют просто
«методом Рунге-Кутта» без всяких указаний
на порядок. Локальная алгоритмическая
ошибка этого метода не превосходит![]() ,
где
,
где![]() -
константа, не зависящая от
-
константа, не зависящая от![]() .
Однако оценить
.
Однако оценить![]() не просто. Это существенный недостаток
метода Рунге-Кутта. Грубое оценочное
правило выбора шага
не просто. Это существенный недостаток
метода Рунге-Кутта. Грубое оценочное
правило выбора шага![]() предложено Коллатцом: если для некоторой
точки
предложено Коллатцом: если для некоторой
точки![]() величина
величина![]()
![]() больше нескольких сотых, то шаг
больше нескольких сотых, то шаг![]() уменьшают.
уменьшают.
4. Общий одношаговый метод.
Метод, алгоритм которого определяется формулой
![]()
где
![]() -
функция аргументов
-
функция аргументов![]() зависит от правой части дифференциального
уравнения
зависит от правой части дифференциального
уравнения![]() ,
называетсяобщим одношаговым методом.
,
называетсяобщим одношаговым методом.
Очевидно, что методы Тейлора и Рунге-Кутта являются частными случаями общего одношагового метода.
Обозначим
через
![]() - решение уравнения
- решение уравнения![]()
![]() с начальным условием
с начальным условием![]() .
.
Теорема(оценка глобальной погрешности общего одношагового метода).
Пусть выполнены следующие условия:
1.
Функция
![]() определена и непрерывна в области
определена и непрерывна в области![]()
![]() и существует константа
и существует константа![]() ,
не зависящая от
,
не зависящая от![]() и
и![]() ,
такая, что в области
,
такая, что в области![]()
![]()
![]()
![]() 2.
Существует константа
2.
Существует константа![]() и целое
и целое![]() такие, что в области
такие, что в области![]()
![]()
![]()
![]()
где
![]() - решение уравнения
- решение уравнения![]() на отрезке
на отрезке![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию![]() .
.
Тогда для глобальной ошибки метода (19) справедлива оценка
![]() где
где![]() ,
,![]() -локальная ошибка округления на
-локальная ошибка округления на![]() -ом
шаге.
-ом
шаге.
Из (20) следует, что глобальная ошибка общего одношагового метода (19) состоит из трех частей:
ошибка при вычислении начального условия,
2)
суммарная алгоритмическая ошибка
метода, характеризуемая величиной
![]() ,
убывающая с уменьшением
,
убывающая с уменьшением![]() ,
,
3)
ошибка округления, представленная
членом
![]() ,
который растет с уменьшением
,
который растет с уменьшением![]() .
.
Из
(20) следует, что попытка уменьшить
алгоритмическую ошибку метода приводит
к уменьшению
![]() и, следовательно, к увеличению ошибки
округления. Кроме того, глобальная
ошибка растет с увеличением длины
интервала, на котором разыскивается
решение дифференциального уравнения.
и, следовательно, к увеличению ошибки
округления. Кроме того, глобальная
ошибка растет с увеличением длины
интервала, на котором разыскивается
решение дифференциального уравнения.
