4 _диффер уравнения
.pdfМетодические рекомендации для студентов 1 курса факультета по РИУ по специальности «лечебное дело»
по самоподготовке к практическому занятию по математике
Тема: Методы решения простейших дифференциальных уравнений. Составление и решение дифференциальных уравнений при решении задач физико-химического и медико-биологического содержания.
Актуальность темы: ознакомление с основными понятиями и методами математического анализа как средства решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности
Цель занятия: научиться решению дифференциальных уравнений 1 порядка с разделяющимися переменными, решению однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, составлению и решению дифференциальных уравнений в прикладных задачах физики, химии.
План изучения темы
1.Понятие дифференциального уравнения и его порядка.
2.Понятие общего и частного решения дифференциального уравнения.
3.Геометрический смысл общего и частного решения дифференциального уравнения.
4.Некоторые виды обыкновенных дифференциальных уравнений:
5.дифференциальные уравнения с разделяющимися переменными;
6.однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
7.Составление дифференциальных уравнений и их решение на примерах задач физико-химического и медико-биологического содержания.
Рекомендуемая литература:
Основная литература:
1.Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-
М.:Медицина, 2004.-232 с.
2.Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков, Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-
Медиа, 2006.-423 с.
Дополнительная литература:
∙Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.-сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.
∙Гмурман В.Е. Теория и математическая статистика. М. «Высшая школа», изд. 5, 2004.
Вопросы для самоконтроля:
1.Дайте определение дифференциального уравнения.
2.Дайте определение порядка дифференциального уравнения.
3.Что называется общим решением дифференциального уравнения?
4.Что называется частным решением дифференциального уравнения?
5.Какое уравнение называется уравнением с разделяющимися переменными?
6.Как найти решение дифференциального уравнения с разделяющимися переменными?
7.Каков общий вид линейного однородного дифференциального уравнения первого порядка?
8.Как найти решение линейного однородного дифференциального уравнения первого порядка?
9.Каков общий вид однородных дифференциальных уравнений
второго порядка с постоянными коэффициентами?
10.Как составляется характеристическое уравнение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами?
11.Каков вид общего решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами в зависимости от знака дискриминанта характеристического уравнения?
Задания на самоподготовку:
1)Найдите общее и частное решения дифференциальных уравнений:
′ = y
1.ln x при x = e, y =1
2.y′ = y 2 при x =1, y =1
2)Найдите общее решение дифференциального уравнения второго порядка с постоянными коэффициентами:
1.y′′+ y′+ y = 0
2.y′′+ 2 y′+ y = 0
3.y′′−6 y ′+8 y = 0xy
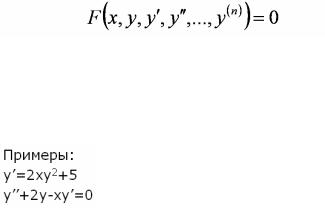
4.
Ориентировочные основы действий:
1.Изучить основные понятия по теме
2.Ответить на вопросы для самоконтроля
3.Проработать примеры решения задач по теме
4.Выполнить задания для самостоятельного контроля
5.Решить контрольные задания по теме
После изучения данной темы студент должен знать: общий вид и теоретические основы решения обыкновенных дифференциальных уравнений.
уметь: решать дифференциальные уравнения первого порядка с разделяющимися переменными и линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами, получить навыки решения прикладных задач на составление дифференциальных уравнений.
Краткая теория
При решении различных задач математики и физики, биологии и медицины довольно часто не удается сразу установить функциональную зависимость в виде формулы, связывающей переменные величины, которые описывают исследуемый процесс. Обычно приходится использовать уравнения, содержащие, кроме независимой переменной и неизвестной функции, ещё и её производные или дифференциалы.
Уравнение, связывающее независимую переменную, зависимую переменную, её производные или дифференциалы обоих переменных называется
дифференциальным уравнением.
Если искомая функция есть функция одного аргумента, то дифференциальное уравнение называется обыкновенным.
Если искомая функция зависит от двух или большего числа аргументов, то уравнение будет содержать частные производные по всем переменными называться дифференциальным уравнением в частных производных.
Порядком дифференциального уравнения называется порядок наивысшей производной или дифференциала, входящих в уравнение.
Решить диф. уравнение – это значит найти неизвестную функцию, которая превращает уравнение в тождество после подстановки этой функции и её производных в уравнение.
Любое диф. уравнение имеет общее и частное решение.
Функция от аргумента х с k произвольными постоянными называется
Общее решение, записанное в неявном виде называется
Частное решение получается из общего решение при наборе конкретных значений констант с учетом тех условий, которым оно должно удовлетворять. Задание таких условий называется начальными условиями.
Задача нахождении частного условия, удовлетворяющего начальным условиям называется задачей Коши.
График решения д.р. называется интегральной кривой. Придавая произвольным постоянным различные значения, можно получить частные решения. На плоскости XOY общее решение представляет собой семейство интегральных кривых, соответствующих каждому частному решению.
Дифференциальные уравнения первого порядка с разделяющимися переменными
f1 (x) f 2 ( y)dy +ϕ1 (x)ϕ2 ( y)dx = 0
Алгоритм решения дифференциальных уравнений первого порядка с разделяющимися переменными
1. Деление обеих частей уравнения на f1 (x)ϕ2 ( y) при условии, что
f1 (x)ϕ2 ( y) ¹ 0 .
После сокращения получаем f 2 ( y) dy + ϕ1 (x) dx = 0 .
ϕ2 ( y) f1 (x)
2.Интегрируем полученное равенство∫ f 2 ( y) dy + ∫ϕ1
ϕ2 ( y) f1
(x) dx = С (x)
3.Разрешаем проинтегрированное выражение относительно y – получаем общее решение д.у.
4.При нахождении частного решения уравнений первого порядка с разделяющимися переменными следующим шагом будет подстановка указанных значений x0, y0 в выражение для общего решения дифференциального уравнения. Тем самым вычисляется численное значение постоянной С=С0.
5.Подстановка в выражение для общего решения дифференциального уравнения полученного значения постоянной С0 – получаем частное решение дифференциального уравнения.
Уравнение вида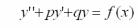 
, где p и q - числа, y = f (x) - функция
аргумента x называются линейными неоднородными уравнениями второго порядка с постоянными коэффициентами.
Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения
Если f (x) = 0 для всех x , то уравнение |
называется |
линейными однородными уравнениями второго порядка с постоянными коэффициентами.
Будем искать решение этого уравнения в виде 
.
Тогда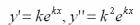 
. Подставив их в уравнение 
получим.
Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
1). Составьте характеристическое уравнение, заменив в данном дифференциальном уравнении y''на exk2, y' на exk, y на exk0=1;
Получаем:
k 2 + pk + q = 0
2). Найдите корни характеристического уравнения k1 и k2
1.k 2 ¹ k1 – действительные;
2.k 2 = k1 = k – действительные;
3.k1,2 = α ± βi – комплексные.
3)В зависимости от вида корней характеристического уравнения, напишите общее решение дифференциального уравнения:
1. |
y = c ek1x |
+ c |
ek2 x |
|
|
|
|
|
||
|
1 |
|
2 |
|
|
|
|
|
|
|
2. |
y = ekx (c x + c ) |
|
|
|
|
|
||||
|
1 |
|
2 |
|
|
|
|
|
||
3. |
y = eαx (c cos βx + c sin βx) , если |
k |
|
= α ± βi где α = - |
p |
; β = q - |
||||
1,2 |
|
|||||||||
|
|
|
|
1 |
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
||
i = + |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|||
p 2 ;
4
Примеры решения задач Пример 1. Найти общее и частное решение дифференциального
уравнения первого порядка с разделяющимися переменными xy'+y = 0 при y = 10, x = 2.
Решение: |
|
|
|
|
|
|
|
1. |
Представим уравнение в виде xdy = −ydx (заменили y ¢ = |
dy |
, |
||||
|
|||||||
|
|
|
|
|
|
dx |
|
|
помножили обе части равенства на dx). |
||||||
2. |
Разделим обе части на ху: |
dy |
- |
dx |
= 0 |
||
|
|
||||||
y x
3. |
Интегрируем |
|
dy |
− |
|
dx |
= С , получаем ln |
|
y |
|
− ln |
|
x |
|
= C1 (С1-сумма |
||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
∫ |
y |
∫ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||||||||||||
|
констант, полученных при интегрировании и константы С) |
||||||||||||||||||||||
4. |
Если постоянную С1 взять в виде C1=lnC0, то ln |
|
y |
|
= ln C0 − ln |
|
x |
|
или |
||||||||||||||
|
|
|
|
||||||||||||||||||||
y = C0 - общее решение дифференциального уравнения.
x
5.Для вычисления частного решения подставим заданные значения для y и x в общее решение дифференциального уравнения,
получим 10 = C0 С0 = 5.
2
6. Подставим полученное значение С0 в общее решение y = 5 -
x
частное решение дифференциального уравнения.
Пример 2.
Решить следующие линейные дифференциальные уравнения второго порядка
1. y²+2y¢=0
|
Решение. Составляем характеристическое уравнение k2+2k=0. Его корни: |
||||||||||||
k |
=0 и k =-2. Общее решение y = C e0 x |
+ C |
e−2 x |
или |
y = C + C |
e−2 x . |
|
||||||
1 |
2 |
1 |
|
2 |
|
|
1 |
2 |
|
|
|||
|
2. y²–2y ¢+9y=0 |
|
|
|
|
|
|
|
|
|
|
||
|
Решение. |
Характеристическое |
|
уравнение |
|
k2–2k+9 = |
0 имеет |
||||||
|
корни k1,2=1 ± |
|
илиk1,2 |
= 1 ± 2 |
|
|
i . |
|
|
||||
комплексные |
1 − 9 |
2 |
Общее |
решение |
|||||||||
дифференциального уравнения y = e x (C1 cos 2
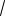2x + C2 sin 2
2x) .
1. y²+4y¢+4y=0
Решение. Характеристическое уравнение k2+4k+4=0 имеет два равных корня k1=k2=2. Общее решение y = e2 x (C`1 x + C2 ) .
Пример 3.
Наэлектризованное тело вследствие несовершенства изоляции постепенно теряет свой заряд. Скорость потери заряда пропорциональна его величине. В начальный момент времени величина заряда равна 100Кл, по истечении 10 мин величина заряда 50Кл. Определить величину заряда через
20 мин.
Решение.
Скорость изменения любого процесса выражается первой производной функции по её аргументу. В данном случае изменяется величина заряда с течением времени.
dq = −αq dt
Знак минус вследствие того, что величина заряда уменьшается с течением времени, α – коэффициент пропорциональности.
Найдем общее решение данного дифференциального уравнения.
∫dqq = −α∫dt ln q = −αt + ln C
ln q = −αt C
q = Ce−αt
Произвольные постоянные, входящие в данное уравнение, С и α, можно найти из начальных условий
t = 0, q =100Кл
t = 600с, q = 50Кл
Получим систему двух уравнений
100 = Ce-α×0 |
|
100 = C |
|
|||
|
|
|
= |
|
||
|
= Ce |
-600α |
|
|
-600α |
|
|
|
= 100e |
||||
50 |
|
|
50 |
|
||
Находим α.
1 = e-600α
2
Логарифмируем полученное равенство
ln 1 = ln e-600α 2
- ln 2 = -600α α = ln 2 = 1,15 ×10-3 600
Итак, уравнение, выражающее зависимость потери величины заряда наэлектризованного тела с течением времени, имеет вид
q =100e-1,15×10−3 t
Через 20 минут величина заряда будет равна
q(1200)=100e-1,15×10−3 ×1200 ≈ 25(Кл)
Контрольные задания:
1)Найти общее и частное решения дифференциальных уравнений:
a)y′ = y 2 при x =1, y =1
b)(x 2 + 4)y′− 2xy = 0 при x =1, y = 5 ;
xy′ = |
y |
|
|
ln x при x = e, y =1; |
|||
c) |
|||
y′ = y
d)ln y при x = 2, y =1
e)yy′/ x + e y = 0
f)x + y′(y + xy)= 0
g)xydx + (x +1)= 0
h)ye2 x dx − (1 + e2 x )dy = 0
2)Найдите общее решение дифференциального уравнения второго порядка с постоянными коэффициентами
a)y′′ + 2 y′ + 2 y = 0
b)y′′ − 6 y′ + 8 y = 0
c)y′′ − 4 y′ + 5 y = 0
d)y′′ + 2 y′ + y = 0
e)y′′ + y′ + y = 0
3)В ультрацентрифугах скорость смещения молекул исследуемого полимера в направлении от оси вращения выражается формулой υ = bω 2 x , где b – постоянная величина, характеризующая данный полимер, ω – угловая скорость вращения центрифуги, x – расстояние от оси вращения до движущейся границы оседающего полимера. Составить уравнение движения границы полимера, если в момент времени t=0 она находилась на расстоянии 0,5 см от оси вращения.
4)Наэлектризованной изолированное тело вследствие несовершенства изоляции постепенно теряет свой заряд. Скорость потери заряда пропорциональнее его величине. В начальный момент времени величина заряда равна 100 Кл, а по истечении 10 мин – 50 Кл. определить величину заряда через 20 мин.
5)Если первоначальное количество фермента равно 1 г, а через 1 ч становится равным 1,2 г, то чему оно будет равно через 5 ч после начала брожения? (Скорость прироста фермента считать пропорциональной его начальному количеству.)
6)В реакцию первого порядка вступает 1000 молекул и за одну секунду 400 из них распадается. Сколько молекул распадается за две сукенды?
7)Согласно теории Смолуховского, процесс быстрой коагуляции
электролитами можно формально приравнять к реакции второго порядка: dc/dt= - kc2, где с – концентрация золя; k >0 – постоянная, характеризующая вероятностьь столкновения частиц. Установить закон концентрации золя, ечсли при t=0 c=c0 и при t=τ c=c0/2.
8)При непрерывном внутрисосудистом введении лекарственного препарата с постоянной скоростью υ изменение его в крови описывается уравнением dm/dt=υ – km , где k – постоянная удаления препарата из крови.
Определить зависимость количества лекарственного препарата в крови от времени при условии, что при t=0 m(0) =0.