
умк_Вабищевич_Физика_ч
.1.pdf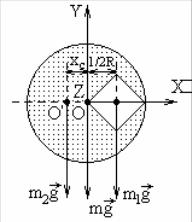
Пример 2.
Внутри диска радиусом R = 105,6 см, изготовленного из плоскопараллельной однородной пластинки, вырезан квадрат таким образом, как показано на рис. 1.8. Найти положение центра тяжести диска с вырезом.
Решение. Нахождение положения центра тяжести однородных тел, имеющих вырез, в рамках школьной программы возможно лишь при условии, что известны положения центров тяжести целого тела и вырезанной части. При этом на чертеже тело с вырезом нужно расположить так, чтобы центры тяжести целого тела и вырезанной части находились в плоскости рисунка на горизонтальной прямой. Тогда силу тяжести целого тела можно представить как сумму двух параллельных сил – силы тяжести вырезанной части и силы тяжести оставшейся фигуры, т.е. тела с вырезом.
Рассмотрим конкретную задачу.
Если бы диск массой m был без выреза, то на него действовала бы сила тяжести mg = m1g + m2 g , где m1, m2 – масса вырезанного квадрата и
масса диска с вырезом соответственно. При этом сила тяжести mg приложена к центру тяжести диска без выреза (к геометрическому центру диска), m1g – к центру тяжести квадрата (к геометрическому центру квадрата), m2 g – в некоторой точке О/, соответствующей центру тяжести диска с выре-
зом. При этом диск находился бы в равновесии.
Запишем уравнение моментов целого диска относительно оси OZ, проходящей через точку О (геометрический центр диска) перпендикулярно плоскости чертежа, считая диск состоящим из двух частей – квадрата и диска с вырезом:
∑M Z = m1g |
R |
− m2 gxc = 0 , |
(1) |
|
|||
2 |
|
|
|
где хс – расстояние от оси OZ до центра тяжести пластинки с вырезом. Выразив массы вырезанного квадрата и диска через плотность и объем
m = 1 |
ρhR2 |
, |
m =ρhπR2 |
(2) |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
(где h – толщина пластинки; ρ – плотность материала, из которого она изготовлена), из (1) – (2) находим
101
|
|
1 m R |
|
|
1 m R |
|
R |
|
|||
xc = |
2 |
1 |
|
|
= |
2 |
1 |
= |
≈ 0,1 м . |
||
m2 |
|
m − m1 |
2(2π −1) |
||||||||
|
|
|
|
|
|
||||||
Ответ: xc = |
|
R |
|
|
≈ 0,1 м. |
|
|
|
|||
2(2π−1) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||
Пример 3.
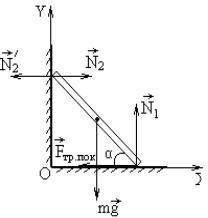
Лестница массой m = 30 кг прислонена к гладкой вертикальной стене под некоторым углом к полу. Коэффициент трения между лестницей и полом µ = 0,3. Определить наименьший угол наклона лестницы к полу, при котором она может оставаться в равновесии, и силу, с которой лестница давит на стену, когда скользит.
Решение. На лестницу кроме силы тяжести mg , приложенной к ее центру масс (сере-
дине), действуют силы: со стороны пола – сила
|
реакции N1 – и сила трения покоя Fтр. пок. ; со |
|
стороны стены – сила реакции N2 (рис. 1.9). |
|
При этом сила трения направлена таким обра- |
|
зом, чтобы препятствовать скольжению лест- |
|
ницы по полу. |
|
Введем систему координат XYZ. Относи- |
Рис. 1.9 |
тельно оси OZ, проходящей через точку О пер- |
пендикулярно плоскости чертежа, момент силы |
|
трения покоя Fтр. |
пок. равен нулю, сила тяжести mg и сила реакции стены |
N2 «вращают» лестницу по часовой стрелке, а сила реакции пола N1 – |
|
против. С учетом этого запишем уравнения равновесия лестницы в виде |
|
||
∑M Z = mg 1 cosα + N2 |
sin α − N1 |
cosα = 0 , |
(1) |
2 |
|
|
|
∑Fx = N2 − Fтр. пок. = 0 , |
|
(2) |
|
∑Fy = N1 − mg = 0 . |
|
(3) |
|
Поскольку сила трения покоя |
|
|
|
Fтр. пок. ≤ Fтр. max = µN1, |
|
|
|
то уравнения (2) – (3) можно записать в виде |
|
|
|
N2 = Fтр. пок. ≤ µN1 ; |
N1 = mg ; |
N2 ≤ µmg . |
(4) |
102
Преобразуем уравнение (1) с учетом выражений (4):
|
mg |
+µmgtgα ≥ mg . |
|
|||
Отсюда находим |
2 |
|
|
|
||
|
|
|
|
|
||
tgα ≥ |
1 |
; |
αmin = arctg |
1 |
≈ 59 . |
|
2µ |
2µ |
|||||
|
|
|
|
|||
Обратимся теперь ко второму вопросу задачи.
При скольжении лестницы сила трения будет равна Fтр = µN1 . Следо-
вательно, сила N2/ (по третьему закону Ньютона N2/ = N2 , с которой лестница будет давить на стену
N2/ = Fтр = µN1 = µmg =88,2 H .
Ответ: αmin = arctg 21µ ≈ 59 ; N2/ = µmg =88,2 H .
Пример 4.
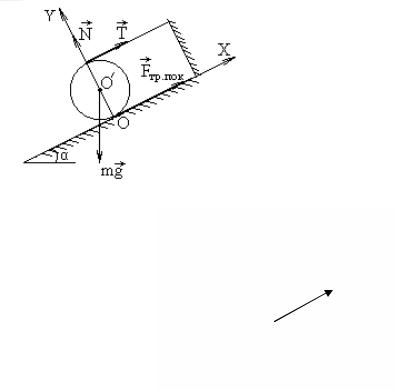
На цилиндр намотана нить, конец которой закреплен на стойке в верхней точке наклонной плоскости так, как показано на рис. 1.10. Коэффициент трения цилиндра о плоскость – µ. При каком максимальном значении угла α цилиндр не будет скатываться с наклонной плоскости?
Решение. На цилиндр действуют четыре силы: сила тяжести mg , сила натяжения нити Т , сила реакции N и
сила трения Fтр. пок. , препятствующая скольжению цилиндра по плоскости.
Так как цилиндр покоится, алгебраи- |
|
ческая сумма моментов сил, действующих |
|
на цилиндр, относительно произвольно вы- |
|
бранной оси равна нулю. Запишем уравне- |
|
ние моментов, например, относительно оси, |
|
перпендикулярной плоскости чертежа и |
Рис. 1.10 |
совпадающей с осью цилиндра, а также |
|
уравнения равновесия для сил в проекциях на оси ОХ и ОY: |
|
∑M Z =TR − Fтр. пок.R = 0 , |
(1) |
∑FX =T + Fтр. пок. − mg sin α = 0 , |
(2) |
∑FY = N − mg cosα = 0 . |
(3) |
103
Выразив из уравнения (1) силу натяжения нити Т и подставив в (2), получим
2Fтр. пок. − mg sin α = 0 . |
(4) |
Поскольку сила трения покоя Fтр. пок. ≤ Fтр. max =µN , то уравнение (4) с учетом (3) можно записать в виде
F |
пок. |
= mg sin α |
≤ µN = µmg cos α . |
|
тр. |
2 |
|
|
|
|
|
|
|
|
Следовательно |
|
|
|
|
tgα ≤ 2µ; |
|
α ≤ arctg2µ; |
αmax = arctg2µ. |
|
Ответ: αmax = arctg2µ. |
|
|
||
104
2. УЧЕБНЫЙ БЛОК «ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА»
Введение
Раздел динамики вращательного движения является одним из основных разделов физики, изучаемой в университете. Это обусловлено, вопервых, достаточно новым материалом, который в школьном курсе физики не изучается. Во-вторых, этот раздел имеет большое значение при изучении других дисциплин: теоретической механики, сопротивления материалов, строительной механики, теории машин и т.д. Поэтому материал этого блока, по сравнению с другими блоками, предлагается на лекции, и не выносится на самостоятельное изучение. Вместе с тем для изучения этого блока необходимо наличие у студентов определенных знаний и умений.
При изучении данного блока студенты
должны знать:
–законы динамики поступательного движения материальной точки;
–понятие момента сил и центра масс;
–законы сохранения механики поступательного движения материальной точки;
иметь представление:
–о правилах векторного и скалярного произведений;
–о методах интегрирования;
–о способах определения центра масс;
–о кинематических характеристиках движения по окружности.
Учебная программа блока
|
Содержание блока |
Форма |
Литература |
|
|
подготовки |
|||
|
|
|
||
|
Динамика твердого тела |
|
||
1. |
Основные понятия: момент импульса, момент |
лекция |
[3] |
|
инерции, момент импульса силы |
||||
|
|
|||
2. |
II закон Ньютона для вращательного движения |
лекция |
[3], [4] |
|
3. |
Закон сохранения момента импульса |
лекция |
[2], [4] |
|
4. |
Кинетическая энергия вращательного движения. |
лекция |
[3] |
|
Работа |
||||
|
|
|||
|
Свободное вращение твердого тела |
|
||
5. |
Понятие о степени свободы твердых тел |
лекция |
[4] |
|
6. |
Момент инерции сложных тел |
лекция |
[2], [3], [4] |
|
105
|
|
|
Окончание табл. |
|
7. |
Вращение тела относительно свободной оси |
лекция |
[4] |
|
8. |
Вращение тела относительно заданной точки |
лекция |
– |
|
9. Гироскопический эффект |
самост. |
[2], [4] |
|
|
Цели обучения
студент должен знать |
студент должен уметь |
– законы динамики вращательного движе- |
– определять моменты сил и плечо сил; |
ния (законы сохранения и II закон Ньютона |
– определятьмоментинерциитвердыхтел; |
для вращательной динамики); |
– определять динамические характеристики |
– понятие и методику определения момента |
вращательного движения на основе зако- |
инерции твердых тел; |
новдинамикивращательногодвижения; |
– способы определения направления век- |
– решать комплексные задачи механики |
торов момента силы, момента импульса; |
сучетомкаченияивращениятвердыхтел |
– понятие степени свободы твердого тела; |
|
– понятие свободной оси и особенности |
|
движения твердого тела со свободной осью |
|
2.1. Краткое содержание теоретического материала
m1
m2
Рис. 2.1
Закон сохранения момента импульса
В динамике систем материальных точек твердого тела известны две величины, которые в замкнутой системе сохраняются: импульс и энергия. Определим еще одну такую величину.
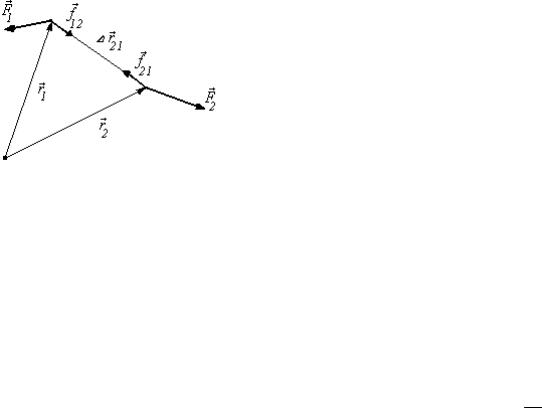
Рассмотрим систему, состоящую из двух взаимодействующих точек, на которые действуют также внешние силы (рис. 2.1). Уравнения движения точек имеют вид
m1υ1 = f12 + F1 и |
m2υ2 = f21 + F2 , |
где υ – производная скорости точек по времени (ускорение).
Умножим первое уравнение на r1 , а второе – на радиус-вектор второй частицы r2 , которые для мгновения времени, можно считать радиусами окружностей, по которым движутся материальные точки m1 и m2 и получим:
m |
r , υ |
|
= r f |
|
+ r F |
|
; |
m |
r ,υ |
|
= r f |
|
+ r F |
. |
1 |
1 1 |
|
1 12 |
|
1 1 |
|
|
2 |
2 |
2 |
2 |
21 |
2 2 |
|
Поскольку векторное произведение rυ эквивалентно dtd [rυ], то получаем уравнение движения в виде
106
m |
d |
[r υ ]= |
r |
, f |
|
+ r F |
; |
m |
d |
[r υ |
2 |
]= r |
, f |
21 |
+ |
r F |
|
(1) |
|||||||||
|
|
|
|||||||||||||||||||||||||
1 |
dt |
|
|
1 1 |
1 12 |
|
1 1 |
|
2 |
dt |
2 |
2 |
|
2 2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Сложив уравнения вместе с учетом p = mυ и − f12 = f21 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
d |
|
|
([r1 p1]+ |
[r2 p2 ]) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
dt |
|
= (r1 − r2 )F12 |
+ r1F1 + |
r2F2 , |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
векторное произведение |
(r |
− r |
), f |
|
= 0 , так как вектора r |
− r |
|
и |
f |
|
парал- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
12 |
|
|
|
|
|
|
|
1 |
2 |
|
12 |
|
|||
лельны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если внешние силы отсутствуют, так как система замкнута, то |
|
||||||||||||||||||||||||||
|
|
|
|
d |
([r1 p1]+[r2 p2 ])= 0 или [r1 p1]+[r2 p2 ]= const . |
|
|
|
|
(2) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Величина L =[rp] носит название момента импульса относительно
точки О.
Закон сохранения момента импульса: в замкнутой системе момент импульса системы тел всегда сохраняется постоянным.
Величина M = rF , как известно, носит название момента силы F
относительно точки О.
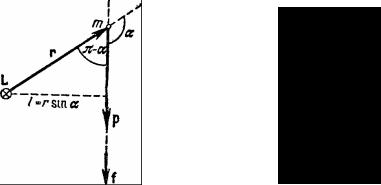
Определение модуля момента импульса показано на примерах (рис. 2.2), где а – момент импульса точки массой m относительно оси ( L = mυl = mυr sin α = pl (3)), а б – момент импульса точки, движущейся по
окружности радиуса R ( L = mυR = pR (4)).
|
|
|
|
|
|
|
а |
|
Рис. 2.2 |
б |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||
Направление вектора L |
определяют по правилу левой руки: если |
||||
четыре пальца ладони направить по направлению плеча импульса, а ладонь расположить так, чтобы импульс входил в ладонь, то момент импульса силы
107
будет направлен по направлению большого пальца ладони, отогнутого на угол 90˚.
Обобщая уравнения (1) и (2), связь момента импульса системы материальных точек с моментами сил, действующих на точки, получаем в виде
|
|
|
|
|
d |
|
|
m |
|
|
|
|
|
|
|
|
L = ∑ ri Fi , |
|
(5) |
||||
|
|
|
|
|
dt |
|
|||||
|
|
|
|
|
|
i |
|
|
|||
m |
ri Fi – суммарный момент внешних сил. |
|
|||||||||
где M = ∑ |
|
||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
Если |
суммарный |
момент |
сил на некоторую ось равен |
нулю |
|||||||
∑M z = 0 , то |
|
|
|
|
|
|
|
|
|||
|
|
d |
Lz = |
∑M z , |
|
d |
Lz = 0 , |
Lz = const |
|
||
|
|
|
|
|
|||||||
|
|
dt |
|
|
|
|
dt |
|
|
||
и момент импульса системы также сохраняется.
Второй закон Ньютона для вращательного движения. Момент инерции тел
На основе уравнений (4) и (5) для материальной точки, движущейся по окружности, можно записать
d(mυR) = FR dt , |
(6) |
где левая часть – изменение момента импульса материальной точки под действием импульса момента силы, представленного правой частью уравнения. Так как υ = ωR , то уравнение (6) можно переписать в виде
mR |
2 |
dω |
= F R = M , |
|
|
dt |
|
||
|
|
|
|
|
или, вводя угловое ускорение ε, в виде |
|
|||
|
|
mR2ε = M , |
(7) |
|
где величина J = mR2 является мерой инертности при вращательном движении и получила название момента инерции. Таким образом, для вращательного движения твердого тела уравнение (7), выражающее Второй закон Ньютона, можно записать в виде
M = JT εT , |
(8) |
где JT – момент инерции тела, εT – мгновенное угловое ускорение тела под действием результирующего момента сил, действующих на тело.
108
Так как масса твердого тела распределена по его объему, то для определения момента инерции тела можно поступать следующим образом:
–разбить тело на микрообъемы dVi;
–определить кратчайшее расстояние ri от dVi до оси вращения тела;
–определить массу микрообъема mi = ρi dVi ;
–определить момент инерции такой массы Ji = miri2 ;
–осуществить операцию суммирования Ji
N |
N |
N |
JT = ∑Ji =∑miri2 |
= ∑ρidVi ri2 . |
|
i=1 |
i=1 |
i=1 |
Операцией, эквивалентной суммированию, является интегрирование функции J по объему тела. Поэтому в общем случае
JT = ∫ρ r2dV , |
(9) |
V
где ρ – плотность вещества тела.
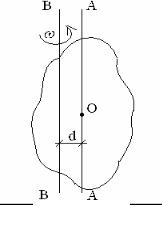
Уравнение (9) позволяет определить J для любого тела (формы и распределения массы) и любой оси вращения этого тела. Однако определение J может быть упрощено в ряде случаев, например, если известен момент инерции тела относительно некоторой оси вращения его, проходящей через центр массы – Jo, а реальная ось вращения параллельно смещена (рис. 2.2).
Рис. 2.2.
АА– ось вращения, для которой известно J0;
ВВ– ось вращения тела, для которой определяется J
Вращение тела относительно оси ВВ с угловой скоростью ω можно представить в виде двух движений:
–движение центра массы mT (точка О) по окружности с радиусом d вокруг оси ВВ;
–вращение тела относительно оси АА.
109
При этом оба движения осуществляются с угловой скоростью ω. Поэтому можно записать
J = J |
o |
+ m d 2 . |
(10) |
|
T |
|
Выражение (10) называется теоремой Штейнера.
Энергия и работа при вращательном движении
Пусть на элементы тела массой mi действуют внутренние fi и внешние Fi силы. Эти силы совершают работу, которая для i-го элемента будет записана в виде формулы
dAi = fiυidt + Fiυidt = fi [ωri ]dt + Fi [ωiri ]dt ,
и которая приводит к движению i-го элемента по окружности относительно некоторой оси с угловой скоростью ω, вектор которой совпадает с осью вращения z.
Тогда для всех элементов тела элементарная работа равна dA = ∑dAi = ω(∑Miвнутр )dt + ω(∑Miвнеш )dt .
Сумма моментов внутренних сил равна 0. Поэтому
dA = ωMdt = ωM ωdt = ωM t dt ,
так как проекция Mω = M z , поскольку ось z совпадает с вектором угловой скорости. Учитывая, что dϕ = ωdt , получаем выражение для работы по повороту твердого тела вокруг оси z на бесконечно малый угол dϕ:
dA = M zdϕ
Для поворота тела на конечный угол ϕ, требуемая работа равна
ϕ
A = ∫dA =M zϕ.
0
Определить энергию вращающегося тела с угловой скоростью ω можно суммированием энергий движения по окружностям всех бесконечно малых элементов (точек) твердого тела, которая является кинетической энергией.
Для одной i-ой точки твердого тела
W |
= |
miυi2 |
= |
miω2Ri2 |
= |
J |
m R 2ω2 |
= 1 ω2 J |
zi |
. |
|
|
|
||||||||
кi |
2 |
2 |
|
2 |
i i |
2 |
|
|||
|
|
|
|
|
||||||
110
