уп_Вабищевич_Физика ч
.1.pdf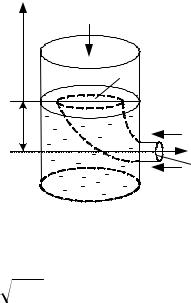
Определим, с какой скоростью вытекает жидкость через отверстие в |
||||||||
сосуде, наполненном жидкостью. Допустим, что в сосуде уровень жидко- |
||||||||
сти поддерживается постоянным. За нулевой уровень отсчета высоты вы- |
||||||||
берем уровень, на котором находится отверстие (рис. 4.2). Выделим линию |
||||||||
тока, которая начинается наверху и заканчива- |
Y |
|||||||
ется в отверстии. Будем считать отверстие |
||||||||
|
||||||||
очень маленьким и давления в верхней и ниж- |
p0 |
|||||||
ней частях его одинаковыми. Запишем уравне- |
||||||||
S0 |
||||||||
ние Бернулли для двух сечений, S0 и |
S : |
|||||||
|
||||||||
|
ρυ2 |
ρυ2 |
|
|
|
p0 υ |
||
где υ0 – |
|
20 + p0 + ρgh = |
2 |
+ p0 , |
h |
|||
скорость движения уровня воды на вы- |
S |
|||||||
соте h ; |
υ – |
скорость вытекания жидкости из |
p0 |
|||||
|
||||||||
сосуда; |
p0 – |
атмосферное давление. По усло- |
Рис.4.2 |
|||||
вию h = const ; υ0 = 0, тогда ρgh = |
ρυ2 |
|||||||
|
||||||||
2 |
, откуда |
|
||||||
|
|
|
|
|
|
|
||
следует, что скорость вытекания жидкости υ = 
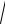2gh .Таким образом, ско-
рость, с которой жидкость вытекает из сосуда, равна скорости, которой об- ладает тело, упавшее с высоты, равной разности уровней отверстия и по- верхности жидкости.
Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу слоев жидкости (условно выделяемых при решении задач) относи- тельно друг друга. Между этими слоями, движущимися друг относительно друга с некоторыми скоростями, действуют силы внутреннего трения (со-
противления). В случае одномерного течения жидкости (вдоль оси х) вели- чина силы трения описывается законом Ньютона
F = −ηS |
dυx |
n , |
(5) |
с |
dy |
|
где n – единичный вектор, совпадающий с направлением вектора скорости
υ, η – коэффициент динамической вязкости (в некоторых случаях исполь-
зуют также коэффициент кинематической вязкости γ = ηρ ), S – площадь со-
прикосновения движущихся слоев; dυx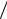 
dy – градиент скорости, т.е. быст- рота изменения скорости слоев в направлении оси Y , перпендикулярной к υx (скорости течения).
Для медленно движущегося небольшого шара радиусом r сила лобо-
вого сопротивления описывается законом Стокса
Fc = −6πrηυ.
161
Закон Стокса лежит в основе лабораторного метода определения вязкости, основанного на изучении падения шариков в вязкой среде.
Характер течения жидкости при обтекании ею какого-нибудь тела
зависит от значения безразмерной величины Re = |
ρυL |
, где ρ – плотность |
|
η |
|
жидкости (газа), υ – средняя (по сечению трубы) |
скорость потока, L – ха- |
|
рактерный размер для поперечного сечения тела. |
|
|
Величина Re называется числом Рейнольдса. Если число Рейнольдса меньше некоторого критического значения, течение жидкости носит лами- нарный характер (слои не перемешиваются), начиная с некоторого значения Re течение жидкости приобретает турбулентный характер.
|
|
|
|
|
|
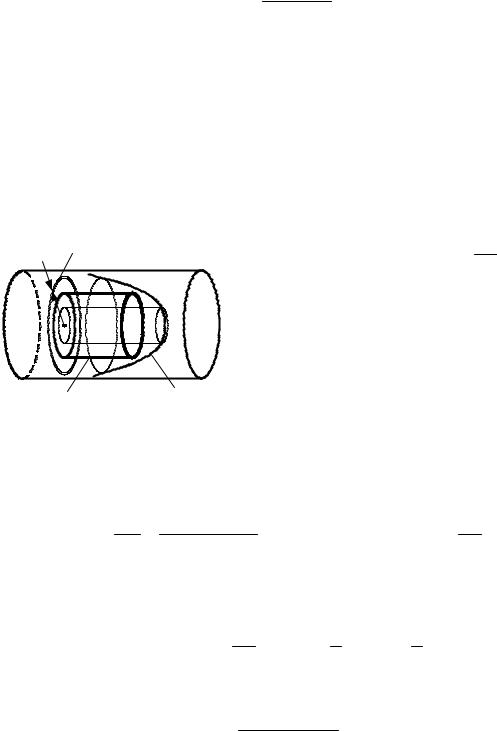
Рассмотрим |
течение |
жидкости |
в |
|
|
|
|
υ1 |
> υ2 |
||||
|
|
|
|
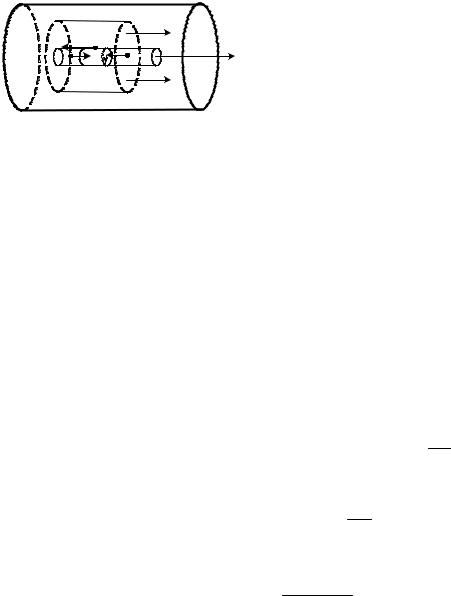
круглой трубе (рис. 4.3). При ламинарном |
|||||
|
|
|
υ2 |
|
|
||||
|
|
|
|
υ |
течении скорость |
жидкости |
меняется |
от |
|
|
Fc |
F2 |
|
|
нуля около стенок трубы до максимально- |
||||
P |
|
|
|
|
1 |
го значения на оси трубы. |
|
|
|
|
r |
|
P |
|
|
|
|||
1 |
F l |
|
|
|
|
|
|
||
|
|
2 |
|
Найдем закон изменения скорости. |
|||||
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
υ= 0 |
|
|
|
|
Выделим воображаемый цилиндрический |
|||
|
|
|
|
|
|
||||
|
Рис. 4.3 |
|
|
|
объем жидкости радиусом r и длиной l. |
||||
|
|
|
|
|
|
При стационарном течении |
этот объем |
||
движется без ускорения. В направлении движения на жидкость действует си-
ла |
давления F = p πr2 , во встречном |
|
|
направлении – |
сила давления |
||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
F |
= p πr 2 |
. Результирующая сил давления имеет модуль |
|
||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = ( p − p |
2 |
)πr2 , |
(6) |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
||
где ( πr2 ) – |
площадь основания цилиндра. |
|
|
|
|
|
|
|
|
||||
|
На боковую поверхность действует тормозящая сила внутреннего трения |
||||||||||||
|
|
|
|
d υ |
|
|
|
|
|
||||
|
|
|
F = −η2πrl |
|
|
, |
|
|
(7) |
||||
|
|
|
|
||||||||||
|
|
|
c |
|
|
|
dr |
|
|
|
|
||
|
|
|
|
|
|
|
|
dυ |
|
|
|||
где 2πrl – |
площадь боковой поверхности цилиндра; |
– |
изменение скоро- |
||||||||||
|
|||||||||||||
dr
сти течения жидкости с расстоянием от оси трубки; dυ < 0 , поскольку ско- dr
рость на оси максимальна.
( p1 − p2 )πr 2 = −η d υ 2πl . dr
Разделив переменные, получим уравнение
dυ = − ( p1 − p2 ) rdr , 2ηl
162
интегрирование которого дает
u = - |
( p1 − p2 ) |
r 2 + C . |
(8) |
|
|||
|
4hl |
|
|
Постоянную C нужно выбрать из условия, что на стенке трубы (т.е. при r = R) скорость обращается в нуль. Это условие выполняется в случае, если
C = ( p1 − p2 ) R2 . 4hl
Подстановка этого выражения в (7) приводит к формуле
u(r) = |
( p - p ) |
|
2 |
- r |
2 |
) = |
( p - p ) |
- |
r2 |
2 |
|
|
||||
1 2 |
(R |
|
|
1 |
2 |
1 |
|
|
R |
|
. |
(9) |
||||
|
|
|
|
|
|
2 |
|
|||||||||
|
4hl |
|
|
|
|
|
4hl |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Скорость жидкости на оси трубы
u = u(0) = |
( p1 − p2 ) |
R2 . |
(10) |
|
|||
0 |
4hl |
|
|
|
|
|
|
С учетом формулы (10) можно записать:
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
u(r) = u |
|
- |
r2 |
|
(11) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
R |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим расход жидкости |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Q , равный объему жидкости, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
протекающей |
через |
поперечное |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
сечение трубы в единицу времени. |
||||||||||
l = υ(r)dt |
Вид функции скорости υ(r) |
Разобьем сечение трубы на кольца |
||||||||||||||||||||
Рис. 4.4 |
|
|
|
|
|
|
|
|
|
шириной |
dr |
(рис. |
|
|
4.4). |
Через |
||||||
|
|
|
|
|
|
|
|
|
кольцо радиусом r толщиной dr |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
пройдет в |
единицу |
|
времени |
объем |
|
жидкости |
dV = u(r )dt × dS , где |
|||||||||||||||
dS = 2πrdr , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dQ = |
dV |
= |
u(r ) |
2prdrdt |
|
|
|
|
|
|
r2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
= 2pru(r )dr = u 2pr 1 - |
|
2 |
dr . |
|
||||||||||
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
0 |
|
|
R |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проинтегрировав это выражение по r в пределах от нуля до R, полу- |
||||||||||||||||||||||
чим поток Q: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = |
R |
u |
|
- |
r2 |
|
= |
1 |
pR2u = |
1 |
|
|
|
|
|
|
(12) |
|||
|
|
∫ |
1 |
|
2 |
2prdr |
|
Su . |
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
R |
|
|
2 |
0 |
2 |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставив в (12) выражение (10), получим формулу Пуазейля
Q = ( p1 - p2 )pR4 . (13) 8hl
163
Из формулы Пуазейля следует, что расход Q сильно зависит от радиуса
трубы, пропорционален отношению ( p1 − p2 ) , т.е. перепаду давления на l
единице длины трубы, а также обратно пропорционален коэффициенту дина- мической вязкости η. Объем жидкости, прошедшей через сечение S за вре- мя t, выражается формулой
V = |
π( p − p )R4t |
|
|
|
1 |
2 |
, |
(14) |
|
|
8ηl |
|||
|
|
|
|
|
из которой найдем коэффициент вязкости
η = |
π( p − p )R4t |
|
|
|
1 |
2 |
. |
(15) |
|
|
8Vt |
|||
|
|
|
|
|
Если жидкость с плотностью |
ρ вытекает из вертикальной трубки |
|||
только под действием собственного веса, то разность давлений на концах трубки равна гидростатическому давлению ρgh , т.е.
p1 − p2 = ρgh , |
(16) |
|||||
где ρ – плотность жидкости; g – ускорение силы тяжести; h – |
высота стол- |
|||||
ба жидкости. |
|
|
|
|
|
|
Тогда с учетом (16) уравнение (15) примет вид |
|
|||||
η = |
πρghR4t |
= |
|
A |
|
|
|
|
|
t . |
(17) |
||
8Vl |
|
|||||
|
|
V |
|
|||
Из выражения (17) следует, что время вытекания некоторого объема V жидкости определяется ее вязкостью и зависит от геометрических раз- меров трубки ( R, l ) и плотности жидкости (ρ) . Поэтому если нам извест-
на величина A = πρghR4 , то, измерив объем жидкости V , вытекающий за
8l
время t , можно рассчитать величину динамической вязкости η согласно (17). В этом состоит суть метода Пуазейля для определения коэффициента динамической вязкости.
Рассмотренные закономерности движения жидкости и тел в жидкости во многих случаях применимы к движению газа и тел в газе, так как при определенных условиях свойства газа оказываются близкими к свойствам жидкости, в частности, при больших скоростях движения газа и тел в газе или при достаточно высокой плотности газа.
164
|
|
|
|
|
|
4.2. Методические указания к лекционным занятиям |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы лекции |
|
Форма |
Литература |
|
Вопросы для самоконтроля |
||||
|
|
изучения |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Давление в жидкости. |
|
|
|
|
1. |
Что называется давлением? |
|
||
|
Сила Архимеда. |
|
|
лекция + |
[5], пп. 1.140 – 1.142 |
2. |
Сформулируйте закон Паскаля. |
|
||
|
Закон Паскаля. |
|
|
самост. |
|
3. |
Что такое гиростатическое давление, чему оно равно? |
|||
|
Стационарное течение |
жидкости |
|
[7], пп. 6.1 – 6.8 |
4. |
Чему равна сила Архимеда? |
|
|||
|
и уравнение неразрывности. |
|
|
|
5. |
Что такое линия и трубка тока? |
|
|||
|
Уравнение Бернулли. |
|
|
|
[8], пп. 8.1 – 8.4 |
6. |
Запишите и объясните уравнение неразрывности. |
|||
|
Сила внутреннего трения. |
|
|
|
7. |
Сформулируйте физический смысл уравнения Бернулли. |
||||
|
Сила сопротивления. |
|
|
|
[10], пп. 28 – 33 |
8. |
Что такое динамический напор? |
|
||
|
Движение |
жидкости в |
круглой |
|
|
9. |
В чем различие ламинарного и турбулентного движения? Что |
|||
|
трубе. |
|
|
|
|
[13], пп. 5.1 – 5.14 |
10. |
такое число Рейнольдса? |
|
|
|
Формула Пуазейля. |
|
|
|
|
Запишите выражение для силы внутреннего трения, от чего она |
||||
|
Методы определения вязкости. |
|
|
|
|
зависит? |
|
|||
|
|
|
|
11. |
От чего зависит скорость течения жидкости вдоль оси трубы? |
|||||
165 |
Применяемость законов движения |
|
|
|||||||
жидкости |
и тел в жидкости |
к |
|
|
12. |
Запишите формулу Пуазейля. |
|
|||
|
движению газов и тел в газах. |
|
|
|
13. |
Что характеризует число Рейнольдса? |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
4.3. Методические указания к практическим занятиям |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Тема |
|
Задачи |
|
|
Рекомендации |
Задачи из сборников |
|||
|
занятия |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Давление жидкостяхи газах |
|
Равновесие |
тел в |
При решении задач на равновесие тел в жидкости необходимо вспомнить |
[11], №№ 1.211 – 1.246 |
||||
|
|
Движение тел в жид- |
условия равновесия тел. |
|
|
[2], №№ 4.1 – 4.20 |
||||
|
|
|
жидкости и газе. |
|
|
|||||
|
|
|
Вытекание жидкостей |
При решении задач на вытекание жидкости из сосудов необходимо пом- |
[12], №№ 12.45 – 12.60 |
|||||
|
|
|
из сосудов. |
|
нить о том, что скорость вытекания зависит от высоты уровня жидкости. |
|
||||
|
|
|
Движение жидкостей |
Задачи данного типа, как правило, решаются с использованием дифферен- |
|
|||||
|
|
|
в трубах. |
|
циального исчисления |
|
|
|
||
|
в |
|
костях и газах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
165
4.3. Примеры решения задач
Пример 1. В жидкости с плотностью ρ1 плавает полый шар объемом
V, изготовленный из материала с плотностью ρ2. Каков объем полости VП ,
если известно, что объем погруженной в жидкость части шара составляет n = 0,75 всего объема шара?
Решение. При равновесии сила тяжести равна архимедовой силе
FA = mg , |
(1) |
где m – масса шара; m = ρ2 (V − VП ) . |
|
Модуль силы Архимеда FA = ρ1gV1 , где V1 – |
погруженный в жид- |
кость объем шара. |
|
После подстановки получаем |
|
ρ2 g (V − VП ) = ρ1gV1 |
|
или с учетом того, что V1 = nV , |
|
ρ2 (V − VП ) = ρ1nV . |
(2) |
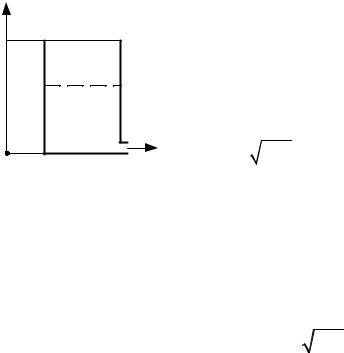
Из (2) получаем выражение для объема полости VП = V (1 − nρ1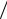 
ρ2 ) .
Ответ: VП = V (1 − nρ1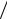 
ρ2 ) .
X
S
h
x 
dx
υ
O |
S0 |
|
Изменение объема уровня жидкости:
Пример 2. Определить время τ вытекания жидкости из сосуда высотой h и площадью осно- вания S, если внизу находится отверстие площа- дью S0 (см. рисунок).
Решение. Известно, что скорость истече- ния жидкости из отверстия определяется форму-
лой υ = 
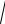2gx , где x – высота уровня поверхности жидкости.
вследствие вытекания связано с изменением
dV = −Sdx . |
(1) |
С другой стороны, это изменение равно объему жидкости, проходя- щему через отверстие,
dV = υS0dt = |
|
|
|
2gxS0dt . |
(2) |
||
166
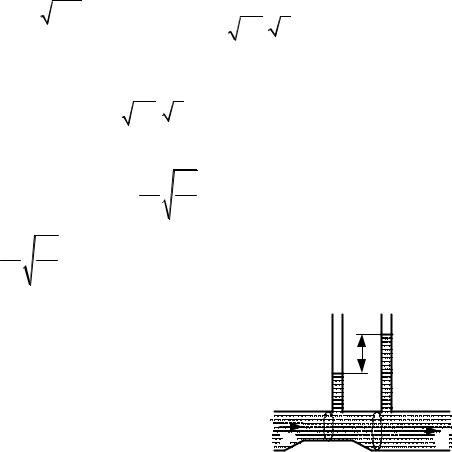
Приравнивая (1) и (2), получаем дифференциальное уравнение
−Sdx = |
|
|
|
S |
|
|
dx |
|
= dt . |
||
2gxS0dt или − |
|
||||||||||
|
|
|
|
|
|
|
|||||
S0 |
|
2g |
|
|
|||||||
|
|
|
|
|
|
|
x |
||||
Интегрируя
0 |
|
S |
|
|
dx |
|
τ |
||
−∫ |
|
|
|
|
= ∫dt , |
||||
|
|
|
|
|
|
|
|
||
S0 |
|
2g |
|
|
|
x |
|||
h |
|
|
|
|
0 |
||||
определяем зависимость времени вытекания от начального уровня:
τ = S 2h .
S0 
g
Ответ: τ = S 2h .
S0 
g
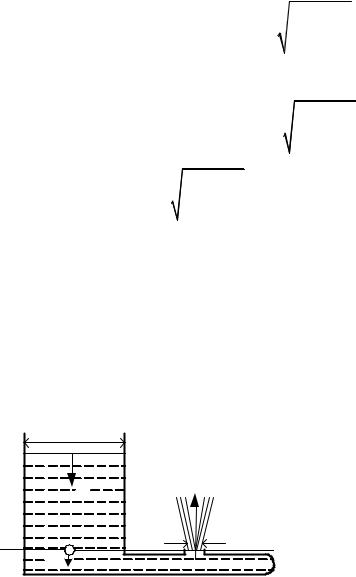
Пример 3. Две манометрические трубки |
|
|
|
установлены на горизонтальной трубе перемен- |
|
|
h |
ного сечения в местах, где сечения трубы равны |
|
|
|
|
|
|
|
S1 и S2 (см. рисунок). По трубе течет вода. Найти |
|
|
|
объем воды, протекающей в единицу времени |
|
|
|
|
|
||
через сечение трубы, если разность уровней во- |
υ |
|
|
S1 |
υ |
||
ды в манометрических трубках равна h. |
|
S2 |
|
|
|
||
Решение. Объем жидкости, протекающий |
|
|
|
в единицу времени, |
|
|
|
V = υ2S2 , |
|
|
(1) |
где υ2 – скорость течения воды в месте сечения S2. |
|
|
|
Запишем уравнение Бернулли для двух сечений: |
|
|
|
ρυ2 |
+ p = |
ρυ2 |
|
(2) |
2 |
1 + p , |
|||
2 |
2 |
2 |
1 |
|
|
|
|
||
где p1 и p2 – статические давления у оснований манометрических трубок, причем p2 − p1 = ρgh .
С другой стороны, из (2) следует, что |
p |
− p = ρυ12 |
− ρυ22 . |
|||
|
|
|
2 |
1 |
2 |
2 |
|
|
|
|
|
||
Приравняв правые части, получаем |
|
|
|
|
|
|
ρgh = |
ρυ2 |
ρυ2 |
|
|
(3) |
|
1 − |
2 |
2 . |
|
|
||
|
2 |
|
|
|
|
|
167
Воспользуемся уравнением неразрывности
υ1S1 = υ2S2 . |
(4) |
Решая совместно систему уравнений (3) – (4), находим скорость
υ2 = S1 |
|
2gh |
|
. |
|
S |
2 |
− S |
2 |
||
|
|
2 |
1 |
|
|
Подставив υ2 в (1), получаем искомый объем жидкости
V = S2S1 |
|
2gh |
|
. |
|
S |
2 |
− S |
2 |
||
|
|
2 |
1 |
|
|
Ответ: V = S2S1 |
|
2gh |
|
. |
|
S |
2 |
− S |
2 |
||
|
|
2 |
1 |
|
|
Пример 4. Вода подается в фонтан из большого цилиндрического бака и бьет из отверстия фонтана со скоростью 12 м/с. Найти: 1. Скорость понижения уровня воды в баке, если диаметр бака равен 2 м, а диаметр от- верстия фонтана 2 см. 2. Давление, под которым вода подается в фонтан. 3. Высоту уровня воды в баке и струи, выходящей из фонтана. Вязкостью воды пренебречь. (Уровень 3).
|
D |
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
1. В |
движущейся |
жидкости |
||
|
|
|
|
|
|
||||
|
υ |
|
|
|
|
выделим два горизонтальных сече- |
|||
|
|
|
|
|
|
|
|
||
|
|
|
υ2 |
|
|
|
|
|
|
|
|
|
|
|
|
ния на уровне отверстия – |
одно в ба- |
||
|
1 |
|
|
|
|
||||
|
|
|
II |
d |
|
ке с диаметром D и второе – в от- |
|||
I |
|
I |
II |
верстии с диаметром d . |
|
||||
|
υ1 |
|
|
|
|
Из |
условия |
неразрывности |
|
|
|
|
|
|
|
υ1S1 = υ2S2 |
следует, что объем воды |
||
V1, протекающий за 1 с через сечение I − I , должен быть равен объему воды |
|||||||||
V2, протекающей через сечение II − II : |
|
|
|
||||||
V1 = V2
или
|
πD2 |
|
= |
πd |
2 |
|
, |
(1) |
|
|
l |
|
l |
2 |
|||
|
|
|
||||||
4 |
1 |
|
4 |
|
|
|
||
|
|
|
|
|
|
|||
где D и d – диаметры бака и отверстия; |
l1 |
и l2 – |
длины цилиндрических |
|||||
столбов жидкости, протекающей за 1 с через сечения I − I и II − II .
168
Так как длины l1 и l2 определяются скоростями течения υ1 и υ2 в се-
чениях I − I и II − II (l1 = υ1 t ; l2 = υ2 t ), равенство (1) можно записать в виде
D2υ = d 2υ |
2 |
, |
|
|
1 |
|
|
|
|
откуда |
|
|
|
|
u1 = u2 |
d |
2 . |
(2) |
|
|
||||
D
Подставив в это равенство числовые значения заданных величин в единицах системы СИ, найдем
υ1 = 12(0,02/2)2 = 0,0012 м/с.
С такой же скоростью будет понижаться уровень воды в баке. Как видно, эта скорость очень мала по сравнению со скоростью струи.
2. Давление р1, под которым вода подается в фонтан, найдем с по- мощью уравнения Бернулли. Это уравнение для идеальной несжимаемой жидкости в условиях данной задачи имеет вид
p + |
ru2 |
= p + |
ru2 |
(3) |
1 |
2 . |
|||
1 |
2 |
2 |
2 |
|
|
|
|
Учитывая, что р2 равно нулю (здесь под давлением мы подразумева- ем избыточное давление над атмосферным), из уравнения (3) получим
|
|
|
|
p = |
ru2 |
ru2 |
|
|
|
|
(4) |
||||||
|
|
|
|
|
2 - |
1 . |
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выразим числовые значения величин в единицах системы СИ: |
|||||||||||||||||
r = 103 кг/м3; |
|
|
|
u1 = 0,0012 м/с; |
|
|
|
|
u2 = 12 м/с. |
||||||||
Подставив их в равенство (4), получим |
|
|
|
|
|
|
|||||||||||
|
|
103 |
×122 |
|
103 × (0,0012)2 |
|
2 |
|
|||||||||
p = |
|
|
|
- |
|
|
|
|
|
|
|
|
|
Н/м |
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Второй член правой части имеет значение, весьма малое по сравне- |
|||||||||||||||||
нию со значением первого члена. Пренебрегая им, получаем |
|||||||||||||||||
|
|
|
|
103 ×122 |
|
|
4 |
|
|
2 |
|
|
|||||
|
p = |
|
|
|
|
|
|
= 7,2 |
×10 |
|
Н/м |
. |
|
||||
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Зная давление р1, можно найти высоту уровня воды в баке по формуле
p1 = ρgh1 ,
откуда h = p1 .
1 rg
169
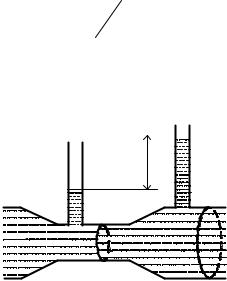
Подставив числовые значения, будем иметь
h = |
7, 2 ×104 |
= 7,35 м. |
||
|
|
|
||
1 |
103 |
×9,81 |
||
|
||||
Зная скорость u2, с которой вода выбрасывается фонтаном, можно найти высоту h2, на которую она будет выброшена:
h = |
u2 |
= |
|
122 |
= 7,35 м. |
2 |
|
|
|||
|
|
|
|||
2 |
2g |
2 |
×9,81 |
||
|
|||||
Подчеркнем, что высота уровня воды в баке равна высоте, на кото- рую поднимется фонтан воды (по правилу сообщающихся сосудов). Конечно, это замечание справедливо, если пренебречь сопротивлением воздуха, а воду считать идеальной (h = 0) .
4.5. Задачи для самостоятельного решения
1. |
Водяной бак в паровозе имеет длину l |
= 4 м. Какова разность |
l уров- |
||||
|
ней воды у переднего и заднего концов бака при движении поезда с ус- |
||||||
|
корением a = 0,5 м/с2? [20,4 см; уровень 5]. |
|
|||||
2. |
Струя воды ударяется о неподвижную плоскость, поставленную под |
||||||
|
углом ϕ = 60° к направлению движения струи. Скорость υ струи равна |
||||||
|
20 м/с, площадь S ее поперечного сечения равна 5 см2. Определить силу |
||||||
|
F давления струи на плоскость [ F = 2rSu2 sin j = 346 Н; уровень 5]. |
||||||
3. |
Насос выбрасывает струю воды диаметром d = 2 см со скоростью |
||||||
|
υ= 20 м/с. Найти мощность P , необходимую для выбрасывания воды. |
||||||
|
[ P = prd 2 u3 |
8 |
= 1,26 кВт; уровень 4]. |
|
|
||
|
|
|
|
|
|
|
|
4. |
Полый медный шар (r = 8,93 г/см3) весит в воздухе 3 Н, а в воде |
||||||
|
(r¢ = 1 г/см3) – 2 Н. Пренебрегая весом воздуха в полости, определите |
||||||
|
|
|
|
|
объем |
внутренней полости |
шара. |
|
|
|
|
|
[68 см3; уровень 2]. |
|
|
|
|
|
|
|
|
||
h |
5. |
Водомер представляет собой горизон- |
|||
|
|||||
|
|
тальную трубу переменного сечения, в |
|||
|
|
которую |
впаяны |
две |
вертикальные |
|
|
манометрические трубки одинакового |
|||
S1 |
|
сечения (см. рисунок). По трубе про- |
|||
S1 |
текает вода. Пренебрегая вязкостью |
||||
|
воды, определить ее массовый расход, |
||||
170