такого вычитания. Здесь вновь работает принцип двойственности: утверждения относительно умножения подобны утверждениям относительно деления.

Пример. Раздаем 12 кругов по 4 круга каждому учащемуся (рис. 7.14 а). Обозначаем вычитанием предметные действия: 1) 12 – 4 = 8, 2) 8 – 4 = 4, 3) 4 – 4 = 0 (или 12 – 4 – 4 – 4 = 0). Из 12-ти по 4 вычитали 3 раза и предметов не осталось. Короткая запись: 12 : 4 = 3. Раздаем 13 кругов учащимся по 4 круга каждому (рис. 7.14 б): 1) 13 – 4 = 9, 2) 9 – 4 = 5, 3) 5 – 4 = 1; или 13 – 4 – 4 – 4 = 1. Из 13-ти по 4 вычитали 3 раза, 1 круг остался не розданным. Короткая запись: 13 : 4 = 3 (ост.1).

Рис. 7.11

Дети овладевают практическими способами деления групп предметов на равночисленные подгруппы по заданному числу предметов в группе (деление по содержанию) как только научаются откладывать равные количества предметов: по одному, по два, по три.

Практическое деление группы предметов на заданное число равночисленных подгрупп (деление на равные части) более сложное, и потому способ, которым дети еще до школы самостоятельно начинают делить предметы на заданное число равных частей – это способ проб и ошибок. Чаще всего пробы бывают двух видов. Первый: количество предметов в каждой части из заданного количества частей определяют исходя из соображений визуального равенства по объему, массе или по другим свойствам, осязаемым органами чувств, а затем проверяют равенство «штук» предметов в частях соответствием один к одному или счетом. Второй: наугад берут по некоторому одинаковому, интуитивно выбранному количеству предметов столько раз, на сколько равных частей нужно поделить. Если при этом все предметы окажутся поделенными, то выбранное число предметов и будет искомым результатом. Если первая попытка неудачна (не хватило предметов или остались предметы), то пробуют другое число предметов.

Существует также алгоритм деления (деление на равные части) группы предметов на заданное число равных частей. На рисунке 7.12 показано деление 12 треугольников на 4 равные по количеству треугольников части. Этот способ описан выше. Он доступен детям, может быть изобретен ими под руководством педагога, подсказан им.

Рис. 7.12

Включение в процесс познания субъектного опыта предметных действий учащихся делает познание осмысленным, личностно значимым. Отметим несовпадение субъектного опыта предметных действий детей и опыта предметных действий учителя, взрослого. У детей этот опыт богат и ярок, так как они занимались этими действиями совсем недавно, весь дошкольный период. У взрослых он по большей части уже забыт. Знание учителем предметных смыслов математических понятий и математических операций позволяет актуализировать опыт соответствующих предметных действий у учащихся.

Смыслы умножения и деления, основанные на понятии величины. Если у сложения и вычитания в теоретико-множественных и величинных смыслах принципиальных различий нет, то в теории числа, основанной на понятии величины, умножение и деление имеют и новые смыслы. Они могут быть перенесены на теоретико-множественные, если количество элементов в множестве рассматривать как величину, которую можно измерять.

Умножение чисел а и b, также как при теоретико-множественном подходе, можно понимать как обозначение «суммирования» – соединения в одно целое соответствующим конкретной величине способом b объектов, числовое значение величины каждого из которых, измеренного в одинаковых для всех частей единицах, равно а (рис. 7.13).

Рис. 7.13

Умножение может быть также понято как операция перехода от более крупных единиц данной величины к другим, более мелким. Так 23 можно понимать как обозначение числового значения величины некоторого объекта в новых, более мелких единицах, где 2 – число, показывающее, сколько новых единиц укладывается в старой единице, иначе, 2 – есть отношение старой единицы, большей, к новой, меньшей, а 3 – числовое значение величины этого объекта в старых, крупных единицах. (Рис. 7.14)

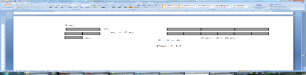
Рис. 7.14

Практическое деление какого-либо предмета на равные по некоторой величине части также как и при теоретико-множественном подходе может быть двух видов, называемых, как мы уже говорили, деление по содержанию и деление на равные части, соответственно, когда задано числовое значение величины части и когда задано число равных по этой величине частей. Деление по содержанию не вызывает трудностей, равно как и его обозначение с помощью чисел и математических знаков. Например, ленту, длина которой равна 60 см, нужно разрезать на части по 30 см каждая. Последовательно отмеряя с помощью линейки по 30 см и считая количество отрезанных частей, получим, что частей будет 2: 60 : 30 = 2 и 60 см : 30 см = 2. Если длина ленты 65 см, то последовательно отмеряя и отрезая по 30 см, получим 2 ленточки по 30 см и ленточку в 5 см, что обозначается делением с остатком: 65 : 30 = 2 (ост. 5) или 65 см : 30 см = 2 (ост. 5 см).

Однако предметная модель деления с остатком с помощью делением предмета на равные по некоторой непрерывной величине части оказывается невозможной. Покажем это на примере деления 11 : 2.

Возьмем бумажную полоску длиной в 11 см. Деление 11 : 2 может быть обозначением деления на равные части заданной длины и деления на заданное число равных частей. Выполним практически (мысленно или реально) оба вида деления. При делении по 2 см (рис. 7.15) полоска в 1 см остается «неразделенной», что и записывается в результате: 11 : 2 = 5 (ост.1)

Рис. 7.15

При делении полоски на 2 равные части (рис. 7.16) перегибанием пополам мы обнаружим, что «неразделенной» части нет, а, значит, нет и остатка. Поэтому введение деления с остатком на основе моделирования практическим делением предмета, геометрической фигуры на заданное число равных по непрерывной величине частей, невозможно.

Рис. 7.16

Деление натуральных чисел на основе понятия величины, кроме рассмотренных двух видов практического деления, в которых мы работаем с одной единицей величины, можно рассматривать с позиций перехода от более мелких единиц величины, к более крупным. Практические действия при этом такие же, как при делении «по содержанию», но результат интерпретируется не как ответ на вопрос «Какова длина (площадь, объем, масса) в новых единицах?» или «Каково числовое значение длины (площади, объема, массы и т.п.) в единицах, где новая единица в целое число раз меньше старой?» (рис. 7.17).

Рис. 7.17

Порядковые смыслы умножения и деления проявляются в способе нахождении результата умножения и деления соответственно присчитыванием (сложением) или отсчитыванием (вычитанием) по два (умножение двух и деление на два), по три (умножение трех и деление на три) и т.д. по натуральному ряду или числовой прямой.

Подготовка к введению умножения и деления заключается в освоении сложения и вычитания, выполнении заданий на сложение одинаковых слагаемых и последовательное вычитание одного и того числа, в счете двойками, тройками и т.д.

• Составьте по данным рисункам суммы (на рисунках изображены группы с одинаковым количеством предметов, пакеты одинаковой, указанной, массы, товары одинаковой, указанной, стоимости и т.п.). • Найди сумму. 5 + 5 + 5 + 5 + 5 + 5 + 6; 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 (М.И. Башмаков, М.Г. Нефедова). • Нарисуй квадрат со стороной в 10 клеток. Размести в нем маленькие квадраты со стороной 4 клетки так, чтобы они не накрывали друг друга. Закрась их. Сколько маленьких квадратов уместилось? Сколько получилось закрашенных клеток? (М.И. Башмаков, М.Г. Нефедова). • Из ряда чисел 1. 2, 3, 4, …20 выпишите ниже каждое второе число, каждое третье, …, каждое десятое. Продолжите получившиеся ряды. • 10 тетрадей нужно разложить в две одинаковые стопки. Сколько стопок получится? 10 тетрадей нужно раздать учащимся по 2 тетради. Сколько учеников получит тетради?

Ведение умножения и деления, мотивация к изучению, планирование изучения умножения и деления. Мотивом к введению действия может быть интерес к нему как к новому действию, которое еще не изучали, но уже слышали о нем, смотрели в учебнике. Сильным мотивом является проблема, решить которую можно введением нового действия. Мотивом введения умножения может быть проблема записи и чтения суммы большого числа одинаковых слагаемых. Например, число всех тетрадей в 7 пачках, в каждой из которых 20 тетрадей, находится сложением: 20 + 20 + 20 + 20 + 20 + 20 + 20. Громоздкость записи, трудности восприятия, чтения при назывании каждого слагаемого и краткость прочтения указанием только двух чисел (20 взято слагаемым 7 раз) приводит к изобретению умножения как рационального обозначения суммы одинаковых слагаемых.

В связи с этим, умножение при введении выступает не как новое, уже имеющееся действие, а как наша договоренность называть и записывать сложение одинаковых слагаемых кратко. До этой договоренности умножения не было. Поэтому при введении умножение – это особый случай сложения, которому мы даем имя «умножение», придумываем для него короткую запись, а затем учимся заменять длинные записи короткими. И лишь постепенно, по мере изобретения способов получения результатов без вычисления суммы одинаковых слагаемых умножение приобретает черты самостоятельного арифметического действия. Очень важно, чтобы учащиеся прожили это становление нового арифметического действия как дело рук своих.

После такого введения умножения необходимо рассмотреть и другие предметные ситуации, которые приводят к сумме одинаковых слагаемых, а значит, к умножению и тем самым задают представленные в начале нашего разговора об умножении предметные смыслы умножения. Ниже приведены примеры соответствующих заданий.

• 1-а. Обозначь выражением количество изображенных предметов, фигур и площадь прямоугольника. 1-б. Выполни задание 1-а двумя способами там, где это возможно. 1-в. Составь несколько равенств с выражениями, полученными при выполнении задания 1-а. (рис. 7.18)

Рис. 7.18

• Замени каждое из выражений равным ему выражением с умножением несколькими способами. Найди значения выражений.

17 + 3 + 17 + 3 + 17 + 3 8 + 8 + 8 + 7 + 7 + 7 12 – 6 + 12 – 6 + 12 – 6 5 + 195 + 5 + 195 + 5 + 195 + 5 (16 + 5 ) + (16 + 5) + (16 + 5)

Особо остановимся на умножении с числом 1 и числом 0. Если умножение вводим как сумму одинаковых слагаемых, а за множителями закрепляем их значения (первый множитель означает слагаемое, а второй множитель количество таких слагаемых), то записи 5 ∙ 1 и 5 ∙ 0 не обозначают умножения, так как в сумме не может быть одно слагаемое или ни одного! Что же делать? Но коль мы «придумали» умножение, то почему бы нам и записи вида 5 ∙ 1 и 5 ∙ 0 не назвать умножением? Давайте назовем! Но у нас нет способа найти число – произведение (значение произведения). Как быть? Воспользуемся присвоенной нами властью: назначим какие-нибудь числа произведениями. Вообще говоря, можно назначить любое, первое пришедшее на ум число. Но было бы неплохо, чтобы назначение этих чисел не помешало свойствам умножения. Одно из таких свойств – переместительное. Для всех случаев умножения, кроме рассматриваемого случая, это свойство справедливо. Логично тогда в качестве произведений взять такие числа, чтобы переместительное свойство выполнялось и для этих случаев. 1∙ 5 = 1 + 1 + 1 + 1 + 1 = 5, а 0 ∙ 5 = 0 + 0 + 0 + 0 + 0 = 0. Тогда назначаем: 5 ∙ 1 = 1∙ 5 = 5, для любого числа ∆ ∙ 1 = 1 ∙ ∆ = ∆; 5 ∙ 0 = 0 ∙ 5 = 0 и ∆ ∙ 0 = 0 ∙ ∆ = 0. Или a ∙ 1 = 1 ∙ a = a и a ∙ 0 = 0 ∙ a = 0.

После введения деления аналогично нужно рассмотреть деление на 0. Запрет деления на 0 может быть мотивирован, например, так. В отличие от умножения на 0 подобрать число в качестве частного при делении некоторого числа на 0 оказалось невозможным. Никто не сумел найти такое число. Люди оказались бессильны. И что же делать? Каждый раз при попытке деления на нуль говорить о том, что мы не смогли «назначить» частное для этого случая? Ну, уж нет! Коль не удалось найти число на эту «должность», то сделаем вид, что мы и не хотели, да и не могли искать! Издадим закон: делить на 0 нельзя! Что теперь мы можем о себе говорить? На нуль мы не делим не потому, что бессильны это сделать, а потому, что есть запрет на такое деление! Но это же совсем другое дело! Мы такие умные, сильные, еще и законопослушные! Такое эмоциональное «прочтение» запрета деления на 0 очень нравится ребятам. И математика вновь показывает, что она создана людьми, что она живая.

Действия с нулем и единицей позволяют акцентировать внимание на поведении чисел в действиях. Число 1 по отношению к умножению и при делении на него ведет себя очень скромно, никак не влияя на результат. Говорят, что 1 – нейтральное число по отношению к умножению и нейтральное справа по отношению к делению. А 0 ведет себя в умножении и при делении нуля агрессивно: в результате любое число превращается в нуль, поглощается нулем. Поэтому в математике 0 называют поглощающим по отношению к умножению, поглощающим слева по отношению к делению. Обычно в школе об этом не говорят. Нуль в делении отличился также тем, что на себя делить запрещает! Такие характеристики чисел придают отношениям и действиям с числами характер отношений между людьми в связи с действиями людей и потому придают числам и действиям с ними личностный характер. А это всегда сказывается положительно на уровне как предметных, так и личностных и метапредметных результатов.

Так как умножение уже третье арифметическое действие, а деление – четвертое, то планирование работы по изучению умножения и деления уже полностью может осуществляться учащимися. Они уже в состоянии сами прогнозировать и планировать свою учебную работу по освоению новых действий. В этот период уже можно предложить учащимся наметить вопросы, на которые нужно будет ответить в процессе изучения умножения и деления. Такими вопросами могут быть: Как читается запись умножения? Как называются компоненты умножения? Какие случаи умножения относятся к табличным? Как построить таблицу умножения? Как можно найти результаты табличных случаев умножения? Что такое деление? Если умножение получено из сложения, то может ли деление быть получено из вычитания? Какими свойствами обладает умножение? Деление? Чтобы окончательно согласовать планы по изучению новых действий, нужно сравнить их с последовательностью изучения, предлагаемую авторами учебника.

К вопросу «Как найти результат умножения?» можно переходить после усвоения основных смыслов умножения. Проведя параллель со сложением, учащиеся обосновывают необходимость построения таблицы умножения однозначных чисел, строят такую таблицу, овладевают навыками табличных вычислений. (Более подробно в 7.4.) Некоторую часть табличных случаев умножения иногда изучают до введения деления, расширяя возможности использования связи деления с умножением.

Деление также вводится на основе предметных действий в предметных ситуациях, задающих теоретико-множественный, величинный и порядковый смыслы числа (см. выше). В процессе таких предметных действий усваиваются не только указанные смыслы, но и связи с умножением, вычитанием. Овладению смыслами умножения и деления те же виды заданий, что и при овладению смыслами сложения и вычитания. Это задания на: а) обозначение соответствующих предметных действий действиями вначале сложением или вычитанием, а затем умножением или делением (включая и деление с остатком); б) по записи или устному названию действия с конкретными числами показать или описать соответствующие предметные действия; в) задания на установление соответствия предметных действий и действий умножения или деления, выражений, содержащих сложение или вычитание и выражений с умножением или делением. Заметим, что универсальной наглядной моделью умножения является прямоугольник, разбитый на равные прямоугольники или прямоугольная таблица. Число равных прямоугольных частей прямоугольника может интерпретироваться как площадь прямоугольника, в единицах, равных площади прямоугольника-части.

Изучение свойств умножения и деления. Прежде всего, отметим, что некоторые свойства умножения и деления могут быть сформулированы учащимися самостоятельно по аналогии со свойствами сложения и вычитания, а затем проверены, обоснованы для некоторых, а затем и любых чисел.

Первым открывается переместительное свойство умножения. Его существование, как и других основных свойств, может быть спрогнозировано при планировании изучения умножения. Учащиеся формулируют его самостоятельно на основе сходства с переместительным свойством сложения. Затем намечаются способы обоснования его справедливости: проверяем вычислениями на нескольких парах чисел, обосновываем для всех чисел.

Для того, чтобы утверждать, что переместительное свойство справедливо для всех пар чисел, можно использовать обоснование на примере подсчета числа ячеек в прямоугольной таблице, которая, при одинаковых размерах ячеек, может быть понята и как прямоугольник, поделенный на равные, прямоугольные части, площадь которых может быть принята за единицу площади а общее их число – значением площади прямоугольника в этих единицах. И в том, и в другом случае очевидно, что число ячеек (прямоугольников-мерок) не зависит от способа подсчета. Рациональных способов два: сосчитать число ячеек (прямоугольников-мерок) в строке, число строк и найти соответствующее произведение; сосчитать число ячеек (прямоугольников-мерок) в столбце и число столбцов и найти соответствующее произведение.

Приведенные рассуждения в состоянии провести любой учащийся, Аналогично может быть обосновано распределительное свойство умножения относительно сложения. Моделью для него может быть прямоугольная таблица с ячейками разного цвета (рис. 7. 19)

Рис. 7.19

По такой таблице легко составляются два числовых выражения:

(3 + 2) ∙ 9 и 3 ∙ 9 + 2 ∙ 9, обозначающих число всех ячеек таблицы, на основании чего (3 + 2) ∙ 9 = 3 ∙ 9 + 2 ∙ 9. И вновь обобщаем на любые числа: так как произведение любой суммы на число можно представить подобным образом, то подобное равенство будет справедливо для любых чисел: (∆ + ⌂) ∙ ☼ = ∆ ∙ ☼ + ⌂ ∙ ☼.

Так как в период изучения свойств умножения и деления учащиеся уже имеют опыт решения текстовых задач, в том числе решения разными арифметическими способами, то еще одним источником открытия свойств может быть решение текстовых сюжетных задач двумя арифметическими способами с записью решения в виде выражения.

Задача. В цветочном магазине составили букеты по 3 цветка одного вида из 36 хризантем и из 21 розы. На сколько больше букетов из хризантем, чем из роз. Решение. Первый способ: 36 : 3 – 27 : 3. Второй способ (36 – 27) : 3. Так как оба выражения дают ответ на вопрос одной и той же задачи, то 36 : 3 – 27 : 3 = (36 – 27) : 3.

Аналогично могут быть изучены и другие, названные в начале этой части главы свойства. С каждым новым свойством степень самостоятельности учащихся нужно увеличивать.

С изучением действий тесно связано рассмотрение числовых рядов, обнаружение закономерностей, на которых построен ряд. Примеры рядов: а) 18, 27, … 72, 81; б) 132, 264, 396, …; в) 3020 , 3220, 3420, 3620, … . Во внеурочной деятельности могут быть рассмотрены ряды и с более сложными зависимостями. Полезны задания на составление рядов.

Средствами углубления представлений об арифметических действиях являются уроки обобщения, задания на составление и определение смысла числовых выражений с парами числовых данных текстовых задач (см. главу о текстовых задачах), уроки или внеурочные занятия – праздники арифметического действия или действий, на которых говорят и показывают достоинства действий, их необычные свойства, говорят о своем добром отношении, делятся впечатлениями от некоторых встреч с ними и т.п., уроки – праздники чисел 0 и 1, как имеющих особые функции в арифметических действиях, праздник «модной одежды» чисел для наилучшего выполнения числами своих функций в арифметических действиях, праздник-конкурс оригинальных способов вычислений.

Уроки обобщения и систематизации уроки завершают изучение каждого блока учебного материала, а также определенные периоды обучения, например, полугодие, учебный год. Обобщающие уроки при изучении арифметических действий призваны обеспечить понимание учащимися связей между действиями, особенности и общие характеристики действий.

7.4. Формирование вычислительных умений у учащихся начальной школы

7.4.1. Понятия, характеризующие вычислительные умения и процесс их формирования. Термин вычислительные умения в теории и методике обучения математике в начальной школе использовался редко. Актуальным он стал в связи с тем, что ФГОС НОО ориентирует на формирование вычислительных умений. На протяжении многих десятилетий при рассмотрении вопросов изучения арифметических действий пользовались термином «вычислительные навыки». Обозначаемое им понятие понималось как «высокая степень овладения вычислительными прие­мами …, значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро»¹. Формирование вычислительных навыков являлось главной задачей изучения в начальной школе арифметических действий и математики в целом. Пути решения этой задачи были реализованы в действовавших тогда учебниках математики, представлены в методических пособиях, обсуждались и совершенствовались в многочисленных публикациях.

Работой, которая задавала ключевые позиции в решении названной задачи, была процитированная выше статья одного из авторов учебников математики, М.А. Бантовой «Система вычислительных навыков», опубликованная в журнале «Начальная школа» в 1975 г, № 10, а затем в № 11 юбилейного для журнала 1993 года в числе наиболее значимых работ из истории журнала. В ней представлены понятия вычислительный прием, вычислительные навыки, теоретическая основа вычислительного приема, названы качества вычислительных навыков (правильность, осознан­ность, рациональность, обобщенность, автоматизм, прочность), даны рекомендации по формированию вычислительных навыков с названными качествами.

Цели формирования вычислительных умений в современной начальной школе – это не только требуемый ФГОС НОО уровень владения учащимися вычислительными умениями. Это также личностные и метапредметные результаты. Личностные результаты: понимание мира и себя в мире, уважение иного мнения, владение начатками алгоритмического мышления и алгоритмической культуры и др. Метапредметные результаты: умения ставить учебные и познавательные цели своей учебной деятельности, выбирать и конструировать учебные действия, направленные на достижение учебных целей (регулятивные универсальные учебные действия - УУД), умения находить личностные основания овладения вычислительными алгоритмами (личностные УУД), устанавливать закономерности, исследуя числовые выражения, таблиц сложения/вычитания и умножения/деления, числовые ряды, умения ставить вопросы, (познавательные УУД), умения сотрудничать с участниками учебного процесса для овладения вычислительными умениями (коммуникативные УУД) и др.

Для подготовки к формированию у учащихся умений «выполнять устно и письменно арифметические действия с числами» (ФГОС НОО) необходимо понять содержание понятий умения выполнять арифметические действия (вычислительные умения), формирование вычислительных умений, и других, связанных с названными.

В педагогической литературе некоторое время велись споры о том, какое психологическое новообразование более высокого уровня: умение или навык. Если понимать навык как «кирпичик» умения, то умение более совершенное качество; если навык считать высоким уровнем развития умения, то навык качество более высокого уровня. Термины «навык», «формирование навыков», «формирование «вычислительных навыков» зачастую ассоциируется с многократным механическим повторением, с механическим заучиванием. Исключение из языка описания изучения арифметических действий названных терминов исключает и ассоциацию с соответствующими способами обучения, которые уже давно признаны неэффективными. Но термин «навык» ассоциируется также со свободным, осознанным, безошибочным, быстрым, доведенным до автоматизма выполнением осваиваемого действия. А эти качества вычислительных умений необходимы учащимся и сейчас. Поэтому термин вычислительные навыки будем использовать для умений с указанными характеристиками, признаком которых может быть способность находить результаты действий по памяти или с помощью алгоритмов быстрых вычислений.

Вычисления являются алгоритмическими процессами. Поэтому вычислительные умения можно понимать как умение выбирать или конструировать для каждого случая вычислений подходящий алгоритм и правильно его применять. Или: владеть вычислительными алгоритмами - это «для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро» (М.А. Бантова).

Формирование вычислительных умений – это процесс овладения учащимися вычислительными алгоритмами, переход от вычислительных алгоритмов на основе предметных действий к алгоритмам с умственными операциями, переход от вычислений с развернутыми рассуждениями и операциями к свернутым.

В 4.2 приведены классификации вычислительных алгоритмов. Выделены устные вычислительные алгоритмы (не содержат операций записи), письменные (записи в заданной форме являются операциями алгоритма), табличные вычислительные алгоритмы (результаты находятся на основе свойств таблицы и свойств действий), алгоритмы вычислений с помощью действий с предметами, инструментами и механическими устройствами (на счетных палочках, счетах, абаках, с помощью масштабной линейки), алгоритмы вычислений на вычислительной технике – алгоритмы калькуляторных вычислений.

На основе классификации вычислительных алгоритмов можно выделить основные виды вычислительных умений: умения вычислять с помощью предметов и инструментов, табличные, устные, письменные, умения вычислять с помощью калькулятора.

Умения вычислять с помощью предметов и инструментов (предметные вычислительные умения) – это умение найти результат действия с помощью счетных палочек, пальцев, условно-предметных рисунков, в том числе моделирующих десятичный состав чисел, а инструментами вычислений можно считать измерительные инструменты, с помощью которых находят результаты арифметических действий на основе величинных смыслов числа. Умения этой группы также как и из группы табличных играют вспомогательную роль в составе вычислительных умений и собственно вычислительную функцию выполняют только в период освоения смыслов соответствующего действия. Однако значимость опыта предметных действий как средства моделирования арифметического действия и его результата, средства создания кинестетического и зрительного его образа велика. Образ действия, зрительный, кинестетический, мышечный, возможно и звуковой, эмоциональный составляет смысловую, и эмоциональную основу устных и письменных вычислительных умений. Наличие этой основы позволяет учащимся конструировать новые способы вычислений, определяет выбор действия при решении текстовых задач, создает чувство уверенности, придает положительную эмоциональную окраску вычислительной деятельности.

Табличные вычислительные умения можно понимать как:

а) умения выполнять сложение и умножение однозначных чисел и соответствующие им действия вычитания и деления с помощью устных вычислительных алгоритмов; б) умение называть результаты табличных случаев действий по памяти (вычислительный навык); в) умение находить результаты действий по заполненной таблице с помощью алгоритма поиска результатов сложения и умножения (находим строку (столбец) первого компонента, столбец (строку) второго компонента, число в ячейке пересечения - результат) и алгоритма поиска результата вычитания и деления (находим строку (столбец) вычитаемого или делителя, ячейку с уменьшаемым или делимым в этой строке (столбце), число столбца (строки) с найденной ячейкой - результат); г) умение находить результаты действий с помощью алгоритмов арифметических действий на основе свойств таблицы и нескольких результатов действий, полученных с помощью устных вычислительных алгоритмов или с помощью предметных действий (такие вычислительные алгоритмы назовем табличными). (4.2)

В структуре вычислительных умений табличные вычислительные умения а) и б) являются базовыми для всех других. Они связаны со многими вычислительными алгоритмами и входят в состав других групп вычислительных умений. Это единственный вид вычислительных умений, относительно которых задача довести уровень владения ими до автоматизма, до автоматизированного вычислительного навыка может быть оправданной и достижимой в начальной школе. Однако этот результат должен достигаться средствами, адекватными современным педагогическим подходам.

Умения в) и г) - вспомогательные при формировании вычислительных умений. Однако они важны, так как являются проявлением универсального учебного действия – считывания информации с таблицы. Кроме того, умения находить результаты с помощью свойств таблицы опирается на умения обнаруживать закономерности, упорядочивать и структурировать информацию, которые являются УУД и признаками метапредметных компетенций работы с информацией.

Следует различать табличные вычислительные алгоритмы - алгоритмически заданные способы вычисления на основе свойств таблицы и табличные вычисления.

В методике обучения математики термины табличные вычисления и внетабличные вычисления используют как обозначение действий соответственно с числами, входящими в таблицы сложения/вычитания и умножения/деления, и с числами, не входящими в них.. Вычисления 7 + 5 = 12; 12 – 5 = 7; 4 ∙ 7 = 28; 28 : 7 = 4 – табличные; 23 + 7 = 30; 30 – 23 = 7; 12 ∙ 3 = 36; 200 : 8 = 25; 600 + 45 = 645; 645 – 600 = 45; 85 : 25 = 3 (ост. 10) - внетабличные.

Устными вычислительными умениями назовем умения пользоваться устными вычислительными алгоритмами, в том числе изобретенными самостоятельно, и умения выполнять вычисления устно, без записей и предметных действий.

Письменными вычислительными умениями назовем умения пользоваться письменными вычислительными алгоритмами арифметических действий, в том числе изобретенными самостоятельно, и умения использовать вспомогательные записи при применении устных вычислительных алгоритмов.

Подчеркнем различия между понятиями устные алгоритмы вычислений, устные вычисления, устные вычислительные умения и между понятиями письменные алгоритмы вычислений, письменные вычисления, письменные вычислительные умения.

Если вычисления проводятся без калькулятора, без записи операций вычислительного алгоритма и промежуточных результатов, без выполнения предметных действий (объединения, удаления предметов или части предмета, деления групп предметов или предмета на равные по некоторому признаку части), то это устные вычисления.

Устные вычисления – это вычисления, выполняемые устно, в уме. В устных вычислениях могут записываться исходные числа и результат, но могут не записываться и они. При выполнении устных вычислений чаще всего используют устные вычислительные алгоритмы. Однако иногда исполнители предпочитают письменные алгоритмы, выполняя соответствующие записи в столбик или уголком мысленно.

При применении устного вычислительного алгоритма запись может не производиться или производиться в любой форме и с любой степенью детализации. Вычисления с помощью устных вычислительных алгоритмов могут устно, а могут сопровождаться развернутой записью, которая будет отражать не только последовательность операций, но и теоретические основы алгоритма, т.е. выполняться письменно. Вычисления 13 – 5; 13 = 10 + 3; 5 – 3 = 2; 10 – 2 = 8; ответ: 13 – 5 = 8 выполнены письменно с помощью устного вычислительного алгоритма. Те же вычисления можно записать «цепочкой»: 13 – 5 = (10 + 3) – 5 = 10 – (5 – 3) = 10 – 2 = 8, записать только результаты всех или некоторых операций (13 – 5; 2; 8). Операции этого алгоритма можно иллюстрировать предметными действиями, а можно выполнить в уме без записей и предметных действий.

При вычислениях с помощью устных вычислительных алгоритмов запись может служить визуальной опорой умственным действиям, показателем осознанности вычислений, средством обоснования вычислений. Обоснование может производиться и устно (теоретические основы алгоритма) и (или) выполнением предметных действий (эмпирические основы алгоритма).

Письменными вычислительными умениями назовем умения пользоваться письменными алгоритмами вычислений и использовать записи как вспомогательное средство в любых вычислениях. Важнейшей составляющей письменных вычислительных умений являются умения читать и записывать числа, устанавливать зависимости между формой записи и выполняемыми операциями, использовать записи как инструмент вычислений.

Учащиеся современной начальной школы выполняют арифметические действия не только устно и письменно, но и на калькуляторе. При вычислениях на калькуляторе задействованы два вида алгоритмов. Первый – это программы выполнения арифметического действия калькулятором, которые разрабатываются программистами и обеспечивают функционирование калькулятора. Мы будем говорить только об алгоритмах второго вида: это алгоритмы действий пользователя по запуску программ и считывания результата работы устройства в соответствии с программой.

Алгоритм выполнения арифметических действий на калькуляторе не требует особых интеллектуальных усилий, и овладеть им нетрудно. Однако для того, чтобы калькуляторные вычисления не мешали, а помогали формированию умений выполнять вычисления устно и письменно, способствовали достижению других метапредметных и личностных результатов, необходимо найти такие их характеристики, которые позволили бы решить названную задачу. В заданиях учебников математики калькулятор вполне обоснованно рекомендуется для проверки письменных вычислений, для выполнения действий при арифметическом решении некоторых текстовых задач и в некоторых других случаях, когда внимание учащихся должно быть сосредоточено не на вычислениях, а на анализе и способах поиска информации, задаваемой результатами вычислений, на способах решения.

Одной из черт калькуляторных вычислений, объединяющей их с некалькуляторными, является возможность ошибок, обусловленных «человеческим фактором», неправильным набором исходных чисел и знаков действий из-за недостаточного владения позиционной записью, из-за нечаянного нажатия не той клавиши, двойного нажатия клавиши, нажатия сразу нескольких клавиш, залипания клавиши и др. Поскольку исключить такие ошибки нельзя, то при считывании результата вычислений на калькуляторе необходимо каждый раз быстро оценивать его правдоподобность. Сделать это можно только с помощью прикидки, прогнозирования, результата и последующей оценки соответствия полученного результата прогнозируемому. Этот же прием проверки работает при устных и письменных вычислениях. Овладение им требует понимания смысла действий, его свойств, зависимостей между компонентами и результатами действий, между изменениями компонентов и изменениями результата действий.

Представленные выше понятия характеризуют а) качества вычислителя, в частности учащегося (вычислительные умения, вычислительные навыки), б) качества вычислительных действий исполнителя (устные, письменные, табличные, предметные, калькуляторные вычисления), в) способ вычисления (вычислительные алгоритмы); г) педагогическую деятельность взаимодействия с учащимися для овладения ими вычислительными умениями и навыками (формирование вычислительных умений и навыков учащихся). Они составляют понятийную основу решений проблемы формирования вычислительных умений у учащихся.

7.4.2. Система работы учителя по формированию вычислительных умений. В общем процессе изучения арифметических действий процессы формирования вычислительных умений занимают одно из главных мест (7.3). Сформулируем несколько важных требований к процессу формирования вычислительных умений, а также вопросы, возникновение которых у учащихся и поиск ответов на них включает учащихся в познавательный и мыслительный процесс, в учебную деятельность, и обеспечивает выполнение соответствующих требований.

• Для начала формирования вычислительных умений необходимо создание содержательных основ вычислительных умений: овладение смыслами действия, свойствами действия, нахождение результатов действия на основе смыслов с помощью действий с предметами или их изображениями. (Что это? Какое это действие?)

• Чтобы формирование вычислительных умений было эффективным, процесс обучения должен обеспечить мотивацию к созданию и обнаружению способов и алгоритмов вычислений, к овладению ими, к постановке и принятию соответствующей учебной задачи. (Как находить результат? Что делать, чтобы найти результат арифметического действия без обращения к действиям с предметами? Как можно складывать (вычитать, умножать, делить? Что делать, чтобы научиться находить результаты этого арифметического действия без обращения к действиям с предметами?)

• Учащимся должен быть обеспечен выбор заданий и способов их выполнения (учебных действий) для овладения алгоритмами действия. (Что делать, чтобы научиться быстро и безошибочно, складывать (вычитать, умножать, делить)? Как выполнять такие задания, чтобы это помогло мне научиться складывать (вычитать, умножать, делить)?)

• Выбор и выполнение учебных действий для выработки умений применять вычислительные алгоритмы. (Где можно применить? Как (что делать, чтобы) научиться применять?) Осознание достоинств и недостатков освоенного алгоритма, встраивание его в систему других освоенных способов вычислений. (Чем хорош и чем плох для меня этот способ вычисления? Есть ли другие?).

• Оценка достижений в ходе самоконтроля и самооценки, внешнего контроля и оценки. (Научился ли я складывать (вычитать, умножать делить) числа … . Научился ли я складывать (умножать), применяя переместительное свойство, правило … ? Научился ли я складывать (вычитать, умножать, делить) круглые числа? умножать на 2? … Как хорошо я умею складывать (вычитать, умножать, делить) … способом? Любыми способами? Какие вычисления у меня еще не получаются? Чему еще стоит научиться?)

Формирование устных и табличных вычислительных умений и навыков. Табличные вычисления занимают особое место среди вычислений. Свободное владение табличными вычислениями означает знание результатов сложения и умножения и соответствующих случаев вычитания и деления для всех однозначных чисел, возможность овладения устными и письменными вычислениями. Достижение такого результата может быть обеспечено разными средствами.

Наилучший образовательный эффект таблица имеет тогда, когда она составлена самими учащимися и они понимают смысл этой работы. Таблица сложения/вычитания составляется в первом классе. Это может быть сделано лишь после того, как учащиеся освоят смыслы сложения смыслы сложения и вычитания и овладеют некоторыми вычислительными алгоритмами. Сложение и вычитание - первые действия, с которыми дети знакомятся в самом начале школьного обучения. Результаты этих действий, прежде чем попадут в таблицу, должны быть найдены с помощью предметных действий, устных вычислительных алгоритмов на основе смыслов и свойств действий, и лишь потом на основе закономерностей таблицы.

Ниже представлены основные способы вычислений, которые можно использовать в начальной школе в период формирования навыков табличного сложения и вычитания. Некоторые из вычислительных алгоритмов этого периода заданы в 4.2.

• 6 + 1 = 7, 7 – 1 = 6, 46 + 1 = 47, 47 – 1 = 46 (свойство натурального ряда: если к число сложить с единицей, то получится следующее число; если из числа вычесть единицу, то получится предыдущее число). • 5 + 3 = 5 + 1 + 1 + 1 = 6 + 1 + 1 = 7 + 1 = 8; 8 – 3 = 8 – 1 – 1 – 1 = 7 – 1 – 1 = 6 – 1 = 5 (присчитывание и отсчитывание по единице на основе порядкового смысла вычитания). • 5 + 3 = 5 + 2 + 1 = 5 + 1 + 2 = 8, 5 – 3 = 5 – 2 – 1 = 3 – 1 = 2 (прибавление и вычитание по частям на основе правила прибавления суммы к числу и вычитания числа из суммы). • 12 – 5 = 7, так как 5 + 7 = 12 (зависимость между сложением и вычитанием: если из суммы вычесть одно слагаемое, то получится второе слагаемое). • 2 + 8 = 8 + 2 = 10 (переместительное свойство, перестановка слагаемых). • 10 + 7 = 17, 17 – 7 = 10, 17 – 10 = 7 (разрядный состав числа).

При изучении табличного умножения и деления, которое происходит на фоне освоенных смыслов умножения и деления, в том числе умножения и деления с единицей и нулем, опирается на опыт изучения табличного сложения и вычитания, уже можно максимально включать учащихся в управление собственной учебной деятельностью. Для актуализации опыта табличного сложения и вычитания, на доске выделим две колонки: «Сложение и вычитание», «Умножение и деление». В первую колонку впишем называемые учащимися свойства сложения и вычитания, примеры соответствующих способов вычислений, во вторую – предположения детей о возможных свойствах и способах вычисления для умножения и деления. В таком сопоставлении со сложением и вычитанием обосновывается необходимость выделения табличных случаев умножения и деления и построения таблицы умножения/деления.

Основным способом умножения до заполнения таблицы умножения/деления является умножение путем нахождения суммы одинаковых слагаемых. Результаты табличных случаев деления на этапе знакомства с этим действием и освоения его смыслов находятся вначале с помощью предметных действий, а затем на основе связи с умножением: 6 ∙ 3 = 6 + 6 + 6 = 18, 18 : 6 = 3, 18 : 3 = 6.

Создание собственно таблиц сложения/вычитания и умножения/деления, которые строятся после овладения смыслами действий и накопления опыта вычислений на основе этих смыслов играет важную роль в формировании вычислительных умений.

Перед построением таблицы сложения/вычитания включаем в уроки (и не только уроки математики) задания, данные которых представлены в таблице, используем термин «таблица», обсуждаем его значение. Для мотивации учащихся к построению и изучению таблицы сложения/вычитания можно использовать прием «точки удивления». Такой точкой удивления может быть сообщение учителя о том, что сложение однозначных чисел и соответствующие случаи вычитания называют табличными. Возникает вопрос о причинах такого названия. Учащихся просят высказать свои предположения. Уточняется само понятие таблицы, рассматриваются образцы таблиц, вводятся термины «строки», «столбцы», ячейка». В разрешении интриги, какое отношение может иметь таблица к сложению и вычитанию, учащиеся приходят к выводу: что в таблицу удобно помещать результаты сложения, чисел, которые помещены в заголовках строк и столбцов таблицы. Далее в диалоговом обсуждении определяется, результаты сложения каких чисел нужно будет поместить в таблицу, почему результаты сложения с 0 и 1 в таблицу можно не заносить, сколько понадобится строк и столбцов. После обсуждения строится сетка таблицы на доске и в тетради, определяются и записываются числа в заголовки таблицы. Аналогично может быть организована работа с введением таблицы умножения/деления.

Заполнение таблицы начинаем слева - направо и сверху - вниз. Когда результаты сложения или умножения (таблица 7.1.) для нескольких пар чисел найдены (с помощью действий с предметами для сложения, с помощью сложения для умножения), то далее для заполнения таблицы можно воспользоваться закономерностями числовых рядов по строкам, столбцам, диагональным ячейкам.

Таблица 7.1.

Таблица сложения/вычитания												Таблица умножения/деления
+	2	3	4	5	6	7	8	9			×		2	3	4	5	6	7	8	9
2	4	5	6	7							2		4	6	8	10				18
3	5	6	7								3		6	9	12	15				27
4	6	7	8								4		8	12	16	20				36
5	7										5			15	20	25
6											6					30
7											7
8											8
9											9

В таблице сложения/вычитания, к примеру, обнаруживаем, что по диагональным линиям справа - налево записаны одинаковые числа, можно заполнить половину таблицы, никаких действий не выполняя. Это кажется удивительным!

Закономерностей, которые могут быть замечены по каждой таблице, много. По таблице сложения/вычитания закономерности доступны учащимся первого класса, овладевшим смыслами сложения, умением вести счет, складывать числа прибавлением по единице и группами.

Возможности таблиц умножения/деления еще более значительны. В таблице умножения/деления на основе обнаруженных закономерностей по нескольким результатам умножения, найденным на основе предметных смыслов или сложения, также могут быть заполнены все ячейки. Самые простые закономерности наблюдаются в каждой строке и столбце: каждое следующее число больше предыдущего на одно и то же число. Интересны последние столбец и строка. Уже первые три произведения, которые легко могут быть найдены сложением, позволяют увидеть, что сумма «цифр» у каждого числа равна 9, что цифры десятков задают последовательность 1; 2; 3; …, а цифры единиц - последовательность 8; 7; 6; … . Заполнение ячеек будет заключаться в написании двух последовательностей цифр.

Огромный мотивационный, познавательный, развивающий потенциал таблиц сложения/вычитания, умножения/деления реализуется тогда, когда они становятся средством и предметом познания.

Таблицу можно использовать для формирования умения «устанавливать закономерность, правило, по которому составлена числовая последовательность, и составлять последовательность по заданному или самостоятельно выбранному правилу (увеличение/уменьшение числа на несколько единиц, увеличение/уменьшение числа в несколько раз)»², для составления числовых рядов, для обсуждения вопросов об особенностях данной таблицы и о таблицах вообще (например, почему таблицы составляют только для однозначных чисел, нет ли интересных закономерностей в таблицах для чисел второго десятка, для нечетных, четных, делящихся на 3 чисел, и др.).

Формирование табличных вычислительных умений начинается с знакомства с арифметическим действием, освоения его смыслов и продолжается после знакомства со свойствами действий и алгоритмами вычислений, основанных на них. Запоминание результатов происходит во всех видах работы над смыслами действий, при открытии и освоении свойств действий, при овладении названиями компонентов действий, при описанной выше работе с таблицами, при выполнении других специальных заданий, которые должны быть разнообразными как по содержанию, так и по форме.

Задания на формирование вычислительных умений должны носить развивающий характер и предоставлять учащимся возможность выполнять их на разных уровнях в соответствии со своими возможностями и зоной своего ближайшего развития. Приведем примеры некоторых видов заданий для формирования табличных вычислительных умений, которые представлены в учебниках и пособиях для начальной школы.

• Вычисли значения сумм (разностей, произведений, частных): …. Запиши получившиеся числа в порядке возрастания (убывания). • Запишите равенства: 1 + 1 = … 2 + 2 = … 3 + 3 = … 4 + 4 = … 5 + 5 = … (1 ∙ 1 = …; 2 ∙ 2 = …; 3 ∙ 3 = …; ) Что вы заметили? • Нарисуй числовой луч. Покажи на нем дугами путь: 0 + 3 + 5 – 8 + 10 – 4 – 6 (0 + 2 ∙ 4 – 3 + 5 – 10) .В какой точке конец пути? • Выполни действия: 6 + 3; 7 – 4; 12 : 3; 7 ∙ 8; 63 : 9; 63 : 8. Измени слагаемые (уменьшаемое и вычитаемое, множители, делимое и делитель) так, чтобы сумма (разность, произведение, частное, частное и омтаток) не изменились. Измени компоненты сложения (вычитания) так, чтобы сумма (разность) увеличилась (уменьшилась) на 1, на 2, …. Измени компоненты умножения (деления) так, чтобы произведение (частное) увеличилось (уменьшилось) в 2 раза. Измени компоненты вычитания так, чтобы разность увеличилась (уменьшилась) на 1, и т.п.

• Восстанови числа в цепочке: 10 + 7 … – 2 … + 4 19 – 5 … + 4 … – 8 … – 2 … – 3 … + 10 … – 5 10. • Составь как можно больше верных равенств, используя числа из 1, 2, 3, 5, 7, 9, 10, 15, 18 и знаки арифметических действий. • Запиши несколько чисел ряда, в котором первое число 5, а каждое следующее больше предыдущего на 2, на 3; на 4, на … (в 2 раза, в 3 раза, …). • Запиши все числа ряда, в котором самое большое число 20, а любые два соседних числа отличаются друг от друга на 4. • Рассмотри суммы (разности, произведения, частные). Запиши значения тех из них, которые помнишь.

Укреплению и развитию вычислительных умений способствуют задания в форме сказочных, веселых сюжетов. Для вычислительной разминки хорошо подходят задачи в стихотворной форме. Полезны задания с познавательной информацией, игры, например, игра в математическое домино или математическое лото.

Следующая группа вычислительных умений формируется на материале внетабличных вычислений.

Формирование умений выполнять внетабличные вычисления. Внетабличные вычисления наиболее богаты возможностями творчества, изобретения оригинальных способов и алгоритмов вычислений, форм их использования и представления. При изучении внетабличных вычислений учащиеся уже могут обсуждать, выбирать и изобретать формы записи. Техника письма позволяет достаточно много писать, а тот факт, что рассматриваемые в этот период алгоритмы устных вычислений никаких требований на форму записи не накладывают, позволяет учащимся экспериментировать, примерять разные формы записи к себе, выбирать удобные, обнаруживать свою индивидуальность и уникальность, т.е. достигать личностных результатов.

Выделим группы внетабличных вычислений, для каждой из которых есть подходящий устный вычислительный алгоритм, хотя к числам каждой группы или к ее части могут быть применены и другие алгоритмы, в том числе письменные. Назовем эти группы и представим соответствующие устные вычислительные алгоритмы развернутой записью применения алгоритма к конкретным вычислениям. Задать их другими способами – словесным предписанием, блок-схемой, формулой, где это целесообразно, вы можете самостоятельно. Заметим, представленные развернутые записи предназначены для передачи информации об алгоритме студентам. Для учащихся алгоритмы могут быть заданы и иначе, записи могут быть короче, а пояснения даны устно, схемой, действиями с предметами.

1. Прибавление и вычитание единицы. Теоретическая основа – порядковый смысл числа. Это первый не предметный способ сложения и вычитания, который осваивают учащиеся. Он раскрывает порядковый смысл числа и рассматривается не только для однозначных, а для любых чисел, относительно которых учащиеся могут назвать следующее число и предыдущее. • 7 + 1 = 8, 14 – 1 = 13, 49 + 1 = 50, 3408 + 1 = 3409, 50 – 1 = 49, 187 – 1 = 186.

2. Действия с круглыми числами, основанные на свойствах позиционной, десятичной системы.

• 10 + 2 = 1дес. + 2ед. = 1дес.2 ед. = 12; 20 + 3 = 23

• 50 + 30 = 5дес. + 3 дес. = 8 дес. = 80; 500 + 300 = 800.

• 12 – 2 = 1дес.2 ед. – 2 ед. = 1 дес. = 10.

• 12 – 10 = 1 дес.2 ед. – 1 дес. = 2 ед. = 2.

• 50 – 30 = 5дес. – 3 дес. = (5 – 3) дес. = 2 дес. = 20

• 10 ∙ 2 = 1 дес. ∙ 2 = (1 ∙ 2) дес. = 2 дес. = 20.

• 20 ∙ 30 = 20 ∙ 10 ∙ 3 = 200 ∙ 3 = 2 сот. ∙ 3 = 6 сот. = 600.

• 40 : 2 = 4 дес. : 2 = (4 : 2) д∙ 3ес. = 2 дес. = 20.

2. Поразрядное выполнение действий.

• 24 + 52 = (20 + 50) + (4 + 2) = 76; 24 + 57 = (20 + 50) + (4 + 7) = 70 + 11 = 70 + 10 + 1 = 81. • 69 – 45 = (60 – 40) + (9 – 5) = 24. • 132 ∙ 3 = 100 ∙ 3 + 30 ∙ 3 + 2 ∙ 3 = 300 + 90 + 6 = 396. • 969 : 3 = 900 : 3 + 60 : 3 + 9 : 3 = 300 + 20 + 3 = 323. • 967 : 3 = 900 : 3 + 60 :3 + 7 : 3 = 300 + 20 + 2 (ост. 1) = 322 (ост. 1).

3. Выполнение действий с помощью свойств (правил) арифметических действий. (Назовите соответствующее свойство или сформулируйте правило для каждого примера вычислений.)

• 17 + 3 = (10 + 7) + 3 = 10 + (7 + 3) = 10 + 10 = 20.

• 48 + 9 = 48 + 2 + 7 = 50 + 7 = 57.

• 48 + 19 = 48 + 2 + 17 = 50 + 17 = 67.

• 63 + 38 = (63 – 2) + (38 + 2) = 61 + 40 = 101.

• 63 + 38. 63 + 40 = 103, 40 – 38 = 2, 103 – 2 = 101. 63 + 38 = 101.

• 35 – 16 = (20 + 15) – 16 = 20 – 16 + 15 = 4 + 15 = 19.

• 32 – 18 = (32 + 2) – (18 + 2) = 34 – 20 = 14.

• 32 – 18. 32 – 20 = 12, 20 – 18 = 2, 12 + 2 = 14, 32 – 18 + 14.

• 32 – 18. 38 – 18 = 20. 38 – 32 = 6, 20 – 6 = 14, 32 – 18 = 14.

• 27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 60 + 21 = 81.

• 75 ∙ 4 = (75 : 5) ∙ (4 ∙ 5) = 15 ∙ 20 = 300.

• 75 4 = 75 ∙ (2 ∙ 2) = 150 ∙ 2 = 300.

• 16 ∙ 25 = 4 ∙ 4 ∙ 25 = 4 ∙100 = 400.

• 72 : 24, 24 ∙ 3 = 72, 72 : 24 = 3.

• 75 : 3 = (15 ∙ 5) : 3 = (15 : 3) ∙ 5 = 5 ∙ 5 = 25.

• 7 : 21. 1∙ 21 > 7, 1 – не частное. 0 ∙ 21 = 0, 0 < 7. 0 – частное; 7 – 0 = 7 , 7 – остаток. 7 : 21 = 0 (ост. 7).

• 273 : 9 = (270 + 3) : 9 = (270 : 9) (ост.3) = 30 (∙ост.3)

Наиболее эффективно становление вычислительных умений тогда, когда дети сами открывают, изобретают, придумывают способы и алгоритмы приведенных вычислений.

Для того, чтобы табличные и внетабличные вычислительные умения стали прочными, безошибочными, быстрыми, выполнение развивающих заданий, изобретение новых способов и алгоритмов вычислений, новых форм записи, полезно чередовать с использованием тренировочных упражнений. Эффективнее такие упражнения выполнять с помощью специальных компьютерных программ. Например, на сайте http://www.mobintech.ru/multiplication/размещена очень простая программа, работая с которой не более 5 минут на каждом уроке и столько же минут дома учащиеся без проблем, в течение короткого станут хорошими вычислителями. Напомним, тренировочные упражнения выполняются после освоения смыслов действий, объединяя тренировку в вычислениях с содержательной, развивающей работой.

Для формирования УУД после обобщения способа вычисления и формулировки алгоритма необходимо сделать предметом осознания и способ получения нового знания, который состоит в следующем: действуя старыми способами получаем ряд результатов и фиксируем их для наблюдения; устанавливаем закономерные связи между исходными числами и результатом; обосновываем наличие таких связей во всех случаях вычислений рассматриваемого вида; формулируем обобщенный способ вычисления, в частности, в форме алгоритма (или предписания алгоритмического вида). При подведении итога урока проговариваем оба результата: алгоритм вычисления на основе записи и путь открытия нового способа действия, алгоритма.

Все виды заданий, которые приведены выше к табличным вычислениям, могут быть использованы и при формировании умений выполнять внетабличные вычисления. Отметим лишь, что в период изучения внетабличных вычислений усиливается роль текстовых сюжетных задач как средства формирования вычислительных умений.

Обучение письменным вычислениям – это обучение сложению, вычитанию, умножению в столбик и делению уголком. Общим в формировании письменных вычислительных умений является то, что письменные алгоритмы вычислений показывают роль формы обозначения информации в повышении эффективности способов получения новой информации с помощью правил преобразования знаков.

Все письменные вычислительные алгоритмы «вырастают» из устных как решение проблемы сохранения промежуточных результатов в устных вычислениях. Устные вычисления трудны потому, что приходится сохранять в памяти результаты некоторых операций, иногда во время выполнения другой операции. Снижение трудностей возможно за счет записей. Осознание названных трудностей, формулирование гипотезы об их снижении за счет формы записи, позволяет учащимся вычленить проблему отыскания компактной, удобной записи вычислений. Такое осознание возможно тогда, когда учащиеся имеют возможность сами конструировать, изобретать способы записей при использовании устных вычислительных алгоритмов.

Переход от алгоритмов устных вычислений к письменным наилучшим образом происходит как поиск компактной записи пошагового применения устного алгоритма поразрядного выполнения действия. Например, поразрядное сложение и вычитание (34 + 53 = (30 + 50) + (4 + 3) = 87; 327 + 452 = (300 + 400) + (20 + 50) + (7 + 2) = 779; 76 – 42 = (70 – 40) + (6 – 2) = 34; 857 – 326 = (800 – 300) + (50 – 20) + (7 – 6) = 531) позволяет увидеть, что при хорошем расположении записи исходных чисел достаточно будет уметь складывать и вычитать однозначные числа. Догадаться, что таким хорошим расположением является запись одного числа под другим, учащиеся могут самостоятельно, «подсмотрев» в учебнике или вспомнив опыт записи цифр друг под другом и сложении многозначных чисел при овладении письмом цифр в начале первого класса, если такой опыт был.

При введении алгоритма письменного умножения опыт сложения и вычитания в столбик также позволяет учащимся активно участвовать в изобретении удобного способа расположения множителей в записи для облегчения умножения. Например, хорошо видны преимущества записи в столбик умножения на однозначное число без перехода через десяток:

223 ∙ 3 = 200 ∙ 3 + 20 ∙ 3 + 3 ∙ 3 = 223

= 600 + 60 + 9 = 669 × 3

669

Даже способ записи чисел при делении, если первая пара чисел требует одного цикла операций алгоритма письменного деления, может быть введен со значимым участием детей. Так, соответствующая запись очень логична при делении с остатком с применением алгоритма подбора частного. Например, при подборе частного в случае 38 : 5 требуется умножение 7 ∙ 5 = 35, вычитание 38 – 35 = 3 и сравнение числа 3 с делителем 5: 3 < 5. Все эти операции удобно записываются при делении уголком.

39 |5

35 |7

4

Важным вопросом формирования вычислительных умений является вопрос о том, на каких парах чисел начинать изучение письменного алгоритма выполнения каждого действия, необходимо ли выделение каких-либо особых случаев и если необходимо, то в какой последовательности рассматривать их.

Отвечая на поставленный вопрос, отметим, что в применении каждого алгоритма можно выделить группы пар чисел таким образом, что алгоритмом выполнения действия с числами из пар разных групп предписываются разные виды операций (что присуще всем письменные вычислительным алгоритмам как алгоритмам разветвленным) или разное количество циклов. Это, в свою очередь, определяет разные уровни трудности применения алгоритма учащимися.

Для письменного алгоритма сложения, сложения в столбик, это две группы, которые принято называть «сложение без перехода через десяток» и «сложение с переходом через десяток». Случаи письменного сложения обычно рассматривают с соблюдением принципа постепенного нарастания трудностей в таком порядке: сложение без перехода через десяток, сложение с переходом через десяток в одном разряде, в двух, трех и т.д. разрядах.

+26 +47 +184 +35972

53 36 239 79348

79 83 423 115320

Изучение письменного вычитания (вычитания в столбик), по нарастанию степени трудности применения алгоритма рассматривают в следующей последовательности: вычитание в случаях, когда • в каждом разряде уменьшаемого не меньше единиц, чем в этом же разряде вычитаемого; • в одном разряде число единиц уменьшаемого меньше, чем в вычитаемом, а в соседнем разряде уменьшаемого не нуль; • в нескольких разрядах число единиц в разряде уменьшаемого меньше числа единиц этого же разряда в вычитаемом и в соседних разрядах не нули; • в разряде уменьшаемого нуль, а в том же разряде вычитаемого не нуль; • в нескольких соседних разрядах уменьшаемого нули, а в этих же разрядах вычитаемого не нули.

Примеры.

_86 _92 _2351 _240 _ 2000

45 53 1782 86 732

21 39 569 154 1268

Алгоритм письменного умножения более сложен, чем алгоритм письменного сложения, и потому более труден в освоении учащимися. Только очень небольшое количество произведений однозначных чисел являются однозначными числами (по 10 произведений с нулем и единицей и 2∙3, 2∙4, 3∙3), а потому лишь малая часть случаев умножения является умножением без перехода через разряд. Поэтому почти всегда приходится выделять устно в промежуточных результатах десятки и единицы, а затем десятки добавлять в произведение единиц следующего разряда. При письменном умножении на многозначное число многократно используется умножение на однозначное число. При этом получается столько неполных произведений, сколько цифр в записи второго множителя. Неполные произведения затем складывают, применяя алгоритм письменного сложения. В письменном умножении есть также особые случаи, для которых алгоритм умножения несколько видоизменяется.

В связи со всеми названными обстоятельствами последовательность изучения письменного умножения такова: • умножение чисел, не оканчивающихся нулем, на однозначное число без перехода через разряд; • умножение чисел, не оканчивающихся нулем, на однозначное число с переходом через разряд; • умножение чисел, оканчивающихся нулем на однозначное число; • умножение чисел, не оканчивающихся нулем на двузначное круглое число; • умножение чисел, не оканчивающихся нулем, на двузначное не круглое число; • умножение чисел, не оканчивающихся нулем, на трехзначное, четырехзначное круглое число; • умножение чисел, не оканчивающихся нулем, на трехзначное не круглое число; • умножение чисел, оканчивающихся нулями.

×234 ×328 ×3210 ×145 ×145 ×582 ×617 × 7321 ×12900

2 4 3 30 30 34 600 153 530

468 1312 9630 4350 4350 438 370200 21963 387

2246 36605 645 .

22898 7321 6837000

1120113

При овладении алгоритмом письменного деления или деления уголком основные трудности возникают у детей при подборе неполного частного, при проверке правильности выбора и в некоторых случаях при записи операций алгоритма и промежуточных результатов. Поэтому и последовательность изучения алгоритма письменного деления может быть следующей: • деление в один цикл (однозначное частное) на двузначное, трехзначные числа в случаях, когда цифра частного легко находится (например, табличный случай или близкий к табличному); • деление в два и более циклов (частное двузначное, трехзначное и т.д.) в случаях, когда цифры частного легко подбираются; • деление в случаях, когда цифра или цифры частного находятся путем подбора частного, в том числе с помощью специальных приемов подбора (рис. 7.20).

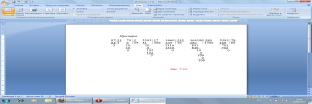
Рис. 7.20

При выполнении письменного деления одним из средств проверки может быть определение количества цифр в частном или определение высшего разряда частного: высший разряд частного есть разряд первого промежуточного (неполного) делимого. Например, при делении 128 092 на 72 первое неполное делимое 128 в делимом представляет единицы тысяч, значит и высший разряд частного – единицы тысяч и частное будет четырехзначным.

Для выработки умений выполнять письменные вычисления необходимы как специальные упражнения, в том числе на выполнение отдельных операций алгоритма, так и решение текстовых задач с применением письменных вычислений. Для проверки вычислений можно использовать как специальные приемы, например, проверка обратным действием, так и калькулятор.

Обучение вычислениям с помощью калькулятора может быть проведено в любом классе, но активно использовать калькулятор можно в третьем – четвертом классах после ознакомления с записью и чтением многозначных чисел. Калькулятор может служить средством тренировки в записи и чтении многозначных чисел. Полезно показать некоторые специальные возможности калькулятора, например, сложение, вычитание, умножение, деление одинаковых чисел при многократном повторном нажатии знака «равно» после выполнения действия с двумя числами. Так, последовательное нажатие клавиш «13 × 5 = = = =» обеспечивает вычисление значения выражения 13 ∙ 5 ∙ 5 ∙ 5 ∙ 5, а клавиш «84 : 4 = = =», значение выражения 84 : 4 : 4 : 4.

Мы уже говорили о необходимости обучать прикидке и оценке результата вычислений, в том числе при вычислениях на калькуляторе. Прикидка результата арифметического действия с натуральными числами может быть основана на прогнозе высшего разряда и определении цифры единиц (за исключением деления с остатком). Например, нужно дать предварительную оценку результата умножения 64356 на 47. Рассуждаем следующим образом. При умножении пятизначного числа на двузначное может получиться число, не менее чем шестизначное, но не более чем семизначное (наименьшее произведение 5-значного и двузначного чисел 10 000∙10 = 100 000 - число шестизначное, а наибольшее 99 999∙99 = 99 999∙(100 – 1) = 9 999 900 – 99 999 будет семизначным). Так как произведение единиц высших разрядов (6∙4 = 24) двузначное число, то искомое произведение будет семизначным числом, в высшем разряде которого может быть 2 или 3 единицы, причем 3 вероятнее (47 близко к 50-ти, а 5∙6 = 30). Последняя цифра произведения 2, так как 6∙7 = 42. Произведение 64356 ∙ 47 = 3 024 732 подтверждает наши прогнозы.

Прикидка устанавливает нижнюю и верхнюю границы результата по высшим его разрядам. При сложении двух чисел сумма может быть числом с количеством цифр как у большего слагаемого или на один больше.

С прикидкой тесно связаны такие действия как округление, приближенные результаты, оценка. «Оценкой называется приблизительный ответ или грубое, предварительное вычисление»³. Округление – это замена точного результата приближенным. Если округление применяется к целым числам, то точный результат, выраженный не круглым числом, заменяется ближайшим круглым. Отсюда и название - «округление». Обучение округлению, оценке – важная часть математического образования младших школьников и формирования вычислительных умений. Такое обучение должно вестись не только в процессе обучения проверке вычислений, но и через задания, специально направленные на формирование указанных действий. Приведем виды таких заданий, часть из них взята из процитированного выше пособия.

• Даны рисунки мелких предметов. Нужно дать оценку их количеству. • Ответьте быстро на вопросы. 1. Какой у вас рост и вес? 2. Сколько времени вы добираетесь до школы? 3. Далеко ли она находится от школы? … • Представлено несколько проездных билетов на поезд с разной стоимостью (билетов в театр, на футбольный матч, …). И даны три приближенных ответа вопрос, сколько стоят все билеты. • Заданы пары чисел. Нужно дать оценку результату арифметическим действиям с ними (найти приближенно результаты арифметических действий с ними). • Округлить заданные числа с заданной точностью. • Используя округление, проверить пробные частные в заданных случаях (первое число – неполное или промежуточное делимое, второе – делитель, третье – пробная «цифра» частного): 137, 26, 4; 137, 26, 7; 137, 26, 5.

Завершая разговор о формировании вычислительных умений и навыков, отметим, что тема эта неисчерпаема и в данной части главы задана лишь основная информация о содержании и направлениях, методах и приемах работы учителя.