Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный институт управления РАНХиГС (СЗАГС)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

задачи по вариантам

.pdf

Скачиваний:

111

Добавлен:

15.05.2015

Размер:

393.05 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Введение Основной тенденцией последних десятилетий является глубокое проникновение математических

методов анализа информации в самые различные сферы деятельности. В частности, владение современными статистическими методами расчета становится необходимым все большему числу государственных служащих, специализирующихся в области экономики, финансов, государственного управления, анализа кризисных ситуаций и т.п. В связи с этим курс теории вероятностей и математической статистики в соответствии с общегосударственным стандартом по специальности 06100 «ГИМУ» является неотъемлемой частью базового курса высшей математики Северо-Западной Академии государственной службы. Вместе с тем, до сих пор отсутствует задачник, позволяющий государственным служащим развить и закрепить навыки самостоятельного использования теоретических методов на практике. Настоящее пособие имеет целью в известной мере устранить этот пробел. Задачник содержит 30 вариантов, каждый из которых содержит 10 задач по основным разделам теории вероятностей, согласованным с основными главами курса теории вероятностей, читаемого в Академии студентам второго курса. Набор задач максимально адаптирован к учебным программам по специальностям 06100 «ГМУ» и 062100 «Управление персоналом».

1. Примеры решения задач.

Приведенные задачи подобраны по темам:

Задача 1 – Прямой подсчет вероятности случайного события на основании классического определения вероятности. Задача 2 – Подсчет вероятности случайного события с использованием теорем сложения и умножения вероятностей. Задача 3 – Определение вероятностей случайных событий с использованием формулы полной вероятности и формулы Байеса.

Задача 4 – Отыскание вероятности успешного выполнения теста, организованного по схеме включения последовательных и параллельных цепочек вопросов.

Задача 5 – по теме дискретные случайные величины и их характеристики. Задача 6 – по теме непрерывные случайные величины и их характеристики. Задача 7 – по теме функции случайных величин.

Задача 8 – по теме системы дискретных случайных величин и их характеристики. Задача 9 – по теме системы непрерывных случайных величин и их характеристики. Задача 10 – по теме нормальный закон распределения.

В тексте задач использованы следующие сокращения и обозначения: ДСВ – дискретная случайная величина.

НСВ – непрерывная случайная величина.

СНСВ – система непрерывных случайных величин. СДСВ – система дискретных случайных величин.

МО – математическое ожидание (EХ=а)

D – дисперсия (DХ= 2 ) .

СКО – средне квадратичное отклонение ( ). ФР – функция распределения F(x), F(x,y).

ПР – функция плотности распределения р(x), р(x,y). КМ - корреляционный момент ( Kxy).

КК - коэффициент корреляции (r XY ).

N(a, ) нормальный закон распределения с математическим ожиданием a и среднеквадратическим отклонением .

Рассмотрим решение типичных задач по каждой теме:

Задача 1. Из ящика, содержащего 8 белых и 6 красных шаров вынимается случайным образом 5 шаров. Какова вероятность того, что вынутые шары – это два белых и три красных.

Решение. Будем решать задачу на основе классического определения вероятности случайного события. Построим вероятностное пространство для опыта, состоящего в «вынимании» случайным образом пяти шаров из четырнадцати. Очевидно, что число n равновозможных исходов такого опыта есть число сочетаний из 14 по 5, то есть

n c145		14 13 12 11 10	2002
		1 2 3 4 5	. Теперь определим число исходов нашего опыта, при которых наступает случайное

событие, вероятность которого мы хотим определить, а именно число исходов этого опыта, при которых вынутые шары будут 2 белых и 3 красных. Из восьми белых шаров можно образовать c82 28 различных комбинаций по два шара.

Аналогично из шести красных шаров можно образовать c36 20 различных комбинаций по три шара. Для определения числа всех «благоприятных» исходов опыта следует рассмотреть каждую комбинацию из c82 28 с каждой комбинацией из c36 20. Таким образом, число m «благоприятных» исходов опыта есть m c82c36 28 20 560. По классическому определению искомая вероятность P mn 2002560 14340 .

Задача 2. Из ящика, содержащего 8 белых и 6 красных шаров вынимается три шара. Какова вероятность того, что все шары красные.

Решение. Эту задачу можно решить тем же способом, как и задачу 1. Но можно также решить ее с применением теоремы умножения вероятностей. Обозначим буквами следующие события:

А={первый вынутый шар оказался красным}. В={второй вынутый шар оказался красным}. С={третий вынутый шар оказался красным}. D={все три шара оказались красными}. События A,B,C – зависимые, так как соотношение белых и красных шаров в ящике после изъятия одного шара зависит от цвета вынутого шара. Очевидно, что целью задачи является вычисление P(D) - вероятности события D. Очевидно также, что событие D есть произведение трех случайных событий:

D A B C . Но по теореме умножения вероятностей: P(D) P(A)PA (B)PAB (C) , следовательно задача сводится

к отысканию вероятностей P(A), PA (B), PAB (C) соответствующих событий. Очевидно, что P(A)=6/14. Вероятность того, что второй шар будет красным при условии, что первый вынутый шар красный, также легко найти. Действительно, если первый шар красный, то в ящике осталось 13 шаров, из которых 8 белых и 5 красных, поэтому PA (B) 5/13.

Условную вероятность PAB (C) найдем аналогично: PAB (C) 4/12 . Итак, по формуле умножения вероятностей имеем: P(D)=(6/14)(5/13)(4/12)=5/91.

Задача 3. В трех студенческих группах отношение к проведению некоторого мероприятия разделилось следующим образом. В группе 211: 12- «за», 13 – «против». В группе 212: 8- «за», 15 – «против». В группах 213 и 214: 22- «за», 4 – «против». Из одной из этих групп выбраны три представителя. Их опрос показал, что один из них – «за», а двое других – «против». Из какой группы наиболее вероятно отобраны представители?

Решение. Обозначим А={трое представителей разделилсь по голосам так, что один из них – «за», а двое других – «против»}, H1={представители выбраны из группы 211}, H2={представители выбраны из группы 212}, H3={представители выбраны либо из группы 213 либо из группы 214}. Заметим, что H1,H2,H3 – несовместны и образуют полную группу. Следовательно, до того как событие А произошло можно говорить, что его вероятность вычисляется по

						3
формуле полной вероятности: P(A) P(Hi )PHi (A). Вероятности «гипотез» Hi легко находятся из условия
						i 1
равнозначности групп при выборе:					P(H1) 1/4,			P(H 2 ) 1/4,				P(H3 ) 2/4 1/2 .			Условные вероятности
события А при различных гипотезах находятся по алгоритму решения задачи 1.
		c121 c132		1213 12		39			c18c152		815 14			120
PH1	(A)	c121 c132		1 1 2		39	PH 2	(A)	c18c152		1 1 2			120
PH1	(A)	3		25 24 23		575	PH 2	(A)	3		23 22 21			253
			c25	25 24 23		575			c23		23 22 21			253
				1 2 3			,				1 2 3			,
			c122c42	22 4 3		33
PH 3	(A)		c122c42	1 1 2		33
PH 3	(A)		3	26 25 24		650
			c26	26 25 24		650
				1 2 3			. Тогда P(A) находится так:
P(A)=(1/4)(39/575)+(1/4)(120/253)+(1/2)(33/650)=0.01696+0.11858+0.02538=0.16092														Теперь можно найти по формуле Байеса
										PA		(H2)	PH 2(A)P(H2) 0.11858			0.737
										PA				P(A)	0.16092	.
вероятность гипотезы H2 при условии, что событие А произошло:																.

Так как «уточненная» вероятность гипотезы H2 больше, чем ½, то уже ясно, что наиболее вероятно, что трое опрошенных

студентов были из 212 группы. В общем случае следовало бы найти «уточненные» вероятности всех гипотез, и выбрать ту из них, у которой эта вероятность больше.

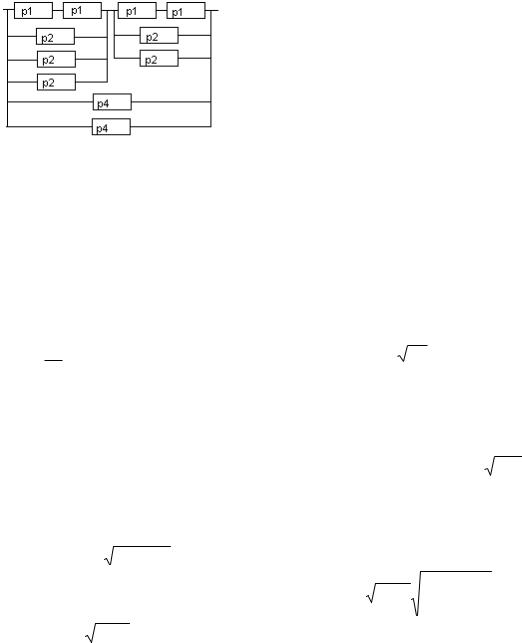
Задача 4. Найти вероятность выполнения абитуриентом экзаменационного теста, состоящего из последовательности вопросов, объединенных в последовательные или параллельные цепочки. При прохождении абитуриентом параллельной цепочки ему разрешается в случае неверного ответа на первый вопрос делать следующие попытки, заключающиеся в ответах на другие вопросы, содержащиеся в параллельной цепочке. Абитуриент снимается с конкурса , если он не сможет ответить ни на один вопрос, имеющийся в параллельной цепочке, а также в случае неверного ответа хотя бы на один из вопросов в последовательной цепочке. Вероятности правильных ответов на каждый из вопросов считаются независимыми друг от друга. На рисунке вопросы теста обозначены совокупностью прямоугольников, внутри каждого из которых приведено значение предполагаемой вероятности правильного ответа абитуриентом на заданный вопрос.

Задачу можно решить, используя теорему умножения вероятностей. Легко видеть, что Абитуриент успешно преодолевает цепочку последовательных вопросов, если он правильно отвечает на каждый вопрос.

Следовательно, вероятность преодоления абитуриентом цепочки последовательных вопросов равна произведению вероятностей его ответов на каждый из вопросов. В случае же параллельной цепочки перемножаются вероятности неправильных ответов. Напомним, что сумма вероятностей правильного и неправильного ответа на любой вопрос равна единице. В силу сказанного вероятность сдачи абитуриентом данного теста может быть вычислена по формуле:

P1 {1 [1 (1 P12)(1 P2)3][1 (1 P12)(1 P2)2]}(1 P4)2

Взадачах 5-9 использованы распределения, приведенные в пособии [1]. Кроме того, использовано распределения Рэлея, индикатор события и геометрическое распределение. Приведем указанные распределения:

Распределение Рэлея:

x p(x) b2 e

x2	, x
	, x	0
2a2
x 0
x 0

b 2

)

F(x) 1

, x

. Геометрический смысл

x 0

распределения Рэлея можно описать так. Пусть имеется равномерное плоское пуассоновское поле точек с плотностью точек на единицу поверхности. Тогда расстояние от какой-либо точки (не обязательно совпадающей с любой из точек поля)

до ближайшей точки поля есть НСВ, подчиняющаяся закону Рэлея с параметром b	1	. При этом количество
	2

точек, находящихся на заданном участке площадью S есть ДСВ, подчиняющаяся закону Пуассона с параметром = S. Отметим также, что если в выбранную точку поместить начало прямоугольной системы координат (X,Y), то координаты

(x,y) ближайшей точки в этой системе подчинены нормальному закону с параметрами EX=EY=0, x= y=b. И обратно: Если X,Y – одинаково нормально распределенные независимые центрированные СВ со среднеквадратичным отклонением

, то величина R	X 2 Y 2 распределена по закону Релея с параметром b= . Если в том же случае нормальные
распределения имеют неодинаковые СКО x y , то величина		x y	X 2	Y 2	имеет распределение Рэлея с
			x2	y2

параметром b x y . Из изложенного следует следующее утверждение. Пусть НСВ подчинена двумерному

нормальному закону, а оси X,Y – есть главные оси распределения. Пусть начало координат находится в центре рассеивания. Пусть имеется эллипс (круг), оси которого совпадают с главными осями распределения, а длины полуосей

эллипса находятся в одинаковой пропорции со среднеквадратичными отклонениями x и y. Тогда вероятность попадания

в эллипс (круг) можно подсчитать по формуле P 1 e	2	где =a1/ x=b1/ y, a1,b1 – длины полуосей эллипса (круга,
в эллипс (круг) можно подсчитать по формуле P 1 e	2	где =a1/ x=b1/ y, a1,b1 – длины полуосей эллипса (круга,
		3

если a1=b1). В заключение напомним, что в одномерном пуассоновском поле расстояние до ближайшей точки есть НСВ, подчиняющаяся показательному закону, а не закону Рэлея.

Геометрическое распределение описывает ДСВ – количество проведенных независимых испытаний до появления первого

успеха, если вероятность успеха в каждом испытании равна p.

Ряд распределения(q=1-p):

…

m 1

…

Числовые характеристики геометрического распределения такие:

1 p

Иногда рассматривают смещенное на единицу геометрическое распределение Y. Это ДСВ, равная числу «неудачных»

испытаний до первого успеха. Очевидно, что Y=X-1 , EY

1 и ряд распределения будет таким:

…

Такое

распределение еще называют распределением Паскаля.

Индикатор I(A) события A– дискретная случайная величина, которая может принимать только два значения: значение ноль, если событие A не происходит, и значение единица, если событие A происходит. Пусть p – вероятность события A. Тогда ряд распределения будет таким:

I(A) 0	1
Pi 1-p	p

Очевидно, что EI(A)=p DI(A)=p(1-p).

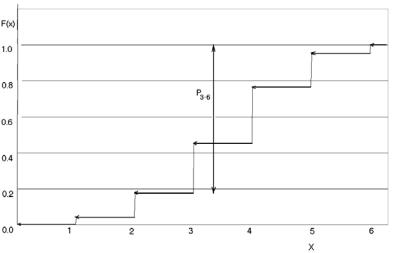
Задача 5. Спортсмен делает шесть бросков мяча в корзину. Вероятность попадания при каждом броске равна р=0.6. Для ДСВ – числа удачных бросков построить ряд распределения и график функции распределения, найти МО и D. Определить вероятность того, что мяч побывает в корзине по крайней мере три раза. Показать эту вероятность на графике функции распределения.

Решение. Так как по условию задачи происходит заданное (шесть) количество "однотипных испытаний", а вероятность "успеха" (попадание мяча в корзину) в каждом испытании постоянна, то "количество успехов" X (число удачных бросков) есть ДСВ, подчиненная биномиальному распределению с параметрами n=6, p=0.8.

Ряд распределения ДСВ X представим в виде таблицы:

X		0			1		2			3		4		5			6
Pi		P0			P1			P2		P5							P6
Вероятности pi				вычислим по известной формуле: pi Cni											pi qn i	, где q=1-p.
P q6		0.46		0.004096					P C1 pq5		6 0.6 0.45				0.036864
0									1	6
P C2 p2q4			15 0.62			0.44			0.13824		P C		3 p3q3		20 0.63 0.43			0.27648
2	6										3		6
P C4 p4q2			15 0.64			0.42			0.31104		P C		5 p5q		6 0.65 0.4 0.186624
4	6										5		6
P p6		0.66		0.046656				. Математическое ожидание EX и дисперсию DX можно не искать по общим формулам, а в
6
данном случае найти их по формулам для биномиального распределения: EX=np=3.6,																				DX=npq=1.44. Вероятность того,
что хотя бы три броска окажутся удачными есть P3 6													= P(3 X 6) P P P							P 0.8208. Построим график
																3		4	5	6

функции распределения и покажем вертикальной "стрелкой-размером" найденную вероятность P3 6 :

Задача 6. Случайная величина X имеет непрерывную функцию распределения:

0		,

ax3			, x 0
F(x)	8		, x 0
	8	,	0	x 2
	1	,	x	2
			x	2

Найти коэффициент а, плотность распределения, дисперсию и математическое ожидание случайной величины X. Найти P(0<X<1). Построить графики ПР и ФР и показать на каждом из графиков найденную вероятность.

Решение. Величину a в данной задаче удобно находить из условия F( ) 1. Так как в данной задаче значение функции

распределения "на бесконечности" равно значению ее в точке x=2 (в силу непрерывности F(x): разрыв функции распределения означает, что мы имеем дело с величиной смешанного типа, а это противоречит нашей "договоренности"

иметь дело только с непрерывно или дискретно распределенными величинами), то можно записать	ax	3	1 при x=2,
	8

откуда следует, что a=1. Плотность распределения найдем как производную от функции распределения:

3x2 p(x) F (x) 8

2		2
EX 3x		xdx	3
0	8		2

,x 0

0 x 2 x 2

2	2	3x	2	9	3
DX x2 p(x)dx Ex2 x2			dx
		8		4	20
0	0

P	P(0 X 1) F(1) F(0)	1
Найдем теперь 10		8 .

Построим графики функции F(x) и плотности p(x) распределения и покажем найденную вероятность на этих графиках. На графике плотности распределения - это площадь криволинейной трапеции (показана серым цветом), а на графике функции распределения найденная вероятность отмечена на шкале ординат:

Задача 7. Непрерывная случайная величина распределена в интервале (1; 5) по закону p(x) xa2 ; Найти a, p(y),

математическое ожидание и дисперсию случайной величины Y (X ) X 2 .

Решение. Для нахождения величины a используем известное свойство плотности непрерывного распределения:

		5	a	dx (a	a)	4 a , откуда следует, что a=5/4. График функции
p(x)dx 1.	Имеем: p(x)dx		a
p(x)dx 1.	Имеем: p(x)dx		2
		1	x	5	1	5

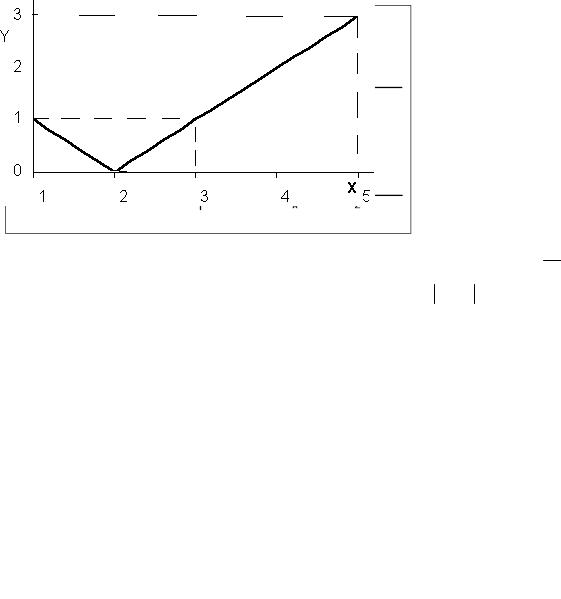
Y (X ) показан на рисунке:

Область значений НСВ Y – промежуток [0,3], причем на промежуток [0,1] приходятся две ветки графика функции, а на промежуток [1,3] – одна ветка. Обратные функции X (Y ) запишутся следующим образом:

0 Y 1	1(Y ) Y			2			2(Y ) 2 Y
	1(Y ) Y 2
1 Y 3	1(Y ) Y 2
Отметим, что в данном примере			1 (Y )						2 (Y )					1	. Применяя формулу Смирнова получим:
			1 (Y )						2 (Y )					1

							0							y 0
				5	(		1				1		)		0 y 1
				4
						(y 2)2						2
p(y) p( (y))		(Y )								(2	y)
										(2	y)
					5		1
					5		1							1 y 3
					4		(y	2)2						1 y 3
					4		(y	2)2
							0							y 3
							0							y 3

Для контроля правильности нахождения p(y) проверим тождество p(y)dy 1. Действительно,

1		5dy		1		5dy				3				5dy
		5dy				5dy								5dy				1
		2			4(2 y)		2				4(y 2)						2	1
0	4(y 2)			0	4(2 y)					1	4(y 2)									.
0				0						1										.
Найдем EY и DY:
EY 03yp(y)dy 015(										1							1				)ydy		3 5			1		ydy
EY 03yp(y)dy 015(								(y 2)						2		(2	y)			2	)ydy		3 5				2	ydy
						4		(y 2)								(2	y)								1 4 (y 2)
(5		5ln3 5ln2) (								1		5ln5					5ln3)						1		5ln2		5ln5 0.779
	6	4		2						3		4					4						2		2		4
DY 3			y2 p(y)dy Ey2						015			(			1							1		)y2dy 3 5			1				y2dy (	1 5ln2	5ln5)2
DY 3			y2 p(y)dy Ey2						015			(	(y 2)				2		(2			y)	2	)y2dy 3 5					2)	2	y2dy (	1 5ln2	5ln5)2
		0								4			(y 2)						(2			y)				1 4 (y			2)			2 2	4
9-5ln5-(				1		5ln2				5ln5)2					0.346.
				2		2				4

Задача 8. Матрица распределения системы двух ДСВ задана таблицей. Найти EX, EY, DX, DY, Kxy,rxy . Построить условный ряд распределения Y(X=16) для указанной ДСВ.

X\Y	1	4	14
12	0.01	0,11	0,06
16	0,16	0,24	0,27
35	0,07	0,03	0,05	распределения для X и Y:
Решение	. Находим сначала ряды			распределения для X и Y:
Y	1	4	14
Pi	0.24	0,38	0,38	далее, суммируя в строках:
(суммирование в столбцах) и				далее, суммируя в строках:
X	12	16	35
Pi	0.18	0,67	0,15

Далее находим EX 12 0.18 16 0.67 35 0.15 18.13 EY 1 0.24 4 0.38 14 0.38 7.08.


DX xi2 pi (EX )2					122 0.18 162 0.67 352 0.15 18.132 52.4931		x	Dx 7.2452
DY y2j				p j (EY )2	12 0.24 42 0.38 142 0.38 7.082 30.6736.	y	Dy	5.538375
Kxy xi				y j pij EXEY 1 12 0.01 1 16 0.16 1 35 0.07 4 12 0.11
4 16 0.24 4 35 0.03 14 12 0.06 14 16 0.27 14 35 0.05 18.13 7.08 3.3304.
r	Kxy			0.082997. Условный ряд распределения при X=16 построим следующим образом. Просуммируем
r
xy		x	y
		x	y

вероятности в строке X=16 матрицы распределения и каждую из вероятностей этой строки разделим на полученную сумму. Это и будут вероятности условного ряда распределения:

Y(X=16)		1		4	14
Pj		0.2388		0,3582	0,4030
Задача 9. ПР для СHСВ выражается формулой.
			A
						, x 10 y 10
P(x,y)	(x 9)		4	(y 9)	4	, x 10 y 10
P(x,y)	(x 9)			(y 9)
				0, иначе
				0, иначе

Найти А, определить являются ли X и Y независимыми СВ или нет. Найти p(x) и p(y), F(x), F(y), F(x,y). Найти P(10<x<11 10<y<11).

Решение. Так как плотность p(x,y) определена на прямоугольной области и может быть разложена на множители

																															A						,		x	10
p1 x p2 y , то НСВ X и Y являются независимыми. Следовательно,																							p1 (x)									1											A
																																9)			4						Значение		A
																												(x				9)									Значение		1
																															0,						иначе
																															0,						иначе
																															A1
найдем из условия p(x)dx 1 , которое для данной НСВ перепишется как																															A1					dx 1.
																													(x 9)					4		dx 1.
																											10		(x 9)
										A									A											A					1
Вычислим этот несобственный интеграл:							10				1		dx 10					1				d(x 9) 1									1	dt 3						A1		, откуда следует, что
Вычислим этот несобственный интеграл:							10	(x			9)4		dx 10					(x 9)4				d(x 9) 1									t 4	dt 3						A1		, откуда следует, что
							A				,	y 10
							1												A 3.				Следовательно A A1A2																	9. Найдем теперь
										4							,		A 3.
A1 3. В силу симметрии p2 (y) (y 9)																	,		1
							0 ,				иначе
							0 ,				иначе
функции распределения F(x),F(y) для X и Y:									F1(x) z							p1(z)dz (при x 10)															x				3dz					1	1
функции распределения F(x),F(y) для X и Y:									F1(x) z							p1(z)dz (при x 10)															x								4	1		3
Следовательно,																															10 (z 9)										(x 9)
Следовательно,
	1																									1
1			, x 10 ,			, в силу симметрии и F2															1									, y			10 ,
1	(x 9)3		, x 10 ,																		1			(y		9)3				, y			10 ,					.
F1(x)	(x 9)3																		(y)					(y		9)3												.
	0 ,		иначе																						0 ,					иначе
	0 ,		иначе																						0 ,					иначе
В силу независимости X и Y:						1					1
						1					1
F(x, y) F1			[1				][1								],				x 10, y 10 ,
			[1		(x	9)3	][1			(y		9)3			],				x 10, y 10 ,								.
	(x)F2 (y)				(x	9)3				(y		9)3															.
									0 ,				иначе
									0 ,				иначе
Найдем P(10	X 11) F			(11)		F (10)			(1				1	) (1						1	) 7				В силу симметрии и
Найдем P(10	X 11) F			(11)		F (10)			(1					) (1							) 7				В силу симметрии и
		1				1						23							13				8
P(10 Y 11) 7 ,												23							13				8		7	7			49 .
P(10 Y 11) 7 ,			следовательно P(10 X 11,10 Y 11)																						7	7			49 .
	8																								8	8			64
Задача 10. Случайная величина X имеет нормальное распределение N(2,3). Найти границы ( , )																																								равномерного
распределения СВ Y,		у которой математическое ожидание и вероятность попадания в интервал (2, 5) были бы такими же

как у СВ X.
Решение. Так как по условию задачи требуется сохранить математическое ожидание E=2, то равномерное распределение
следует строить на участке (2-а, 2+а), то есть =2-а, =2+а.
Найдем вероятность попадания в интервал (2, 5):
P(2<X<5)=Ф(	5 2	) Ф(		2 2	) Ф(1) Ф(0) 0.3413 0 0.3413 Так как длина области изменения НСВ Y равно

3			3
2a, а для этого равномерного распределения P(2<Y<5)= 5 2							, то приравнивая полученное выражение вычисленному
			3			2a
значению получим:						4,395. Следовательно, =2-4,395=-2,395, =2+4,395=6,395.
			2 0,3413

2. Варианты контрольных работ.

Задачи номер 4 и номер 8 имеют одинаковый текст для всех вариантов, поэтому здесь приведем этот текст: Задача 4. Дана структура экзаменационных тестов с прилагаемой вероятностью правильных ответов на задаваемые вопросы. Найти вероятность успешного прохождения абитуриентом всего теста. Последовательная «цепочка»

прямоугольников означает, что прохождение этой части теста есть правильный ответ на каждый «вопрос-прямоугольник». Параллельная «цепочка» прямоугольников означает, что прохождение этой части теста есть правильный ответ хотя бы на один из «вопросов-прямоугольников».

Задача 8. Матрица распределения системы двух ДСВ задана таблицей. Найти EX, EY, DX, DY, Kxy, r xy . Построить

условный ряд распределения для указанной ДСВ.

Рисунки и таблицы для задач номер 4 и номер 8 для всех вариантов приводятся в конце пособия.

ВАРИАНТ №1.

1.В партии 12 деталей, 5 из них бракованные. Какова вероятность того, что 2 наугад выбранные детали окажутся бракованными?

2.В лифт семиэтажного дома вошли 3 человека. Каждый из них, начиная со второго этажа, может выйти на любом этаже с

равной вероятностью. Найти вероятность того, что все выйдут на разных этажах.

3. В отделе 5 «отличных», 7 «хороших», 4 «удовлетворительных» и 4 «слабых» сотрудников. Вероятности того, что сотрудники выполнят некое поручение, для каждой категории соответственно равны 0.9 0.7 0.6 и 0.5. Наудачу вызванный сотрудник из трех однотипных поручений выполнил два поручения и не выполнил одно. Какова вероятность того, что этот сотрудник «хороший»?

5. Вероятность встретить автомобиль с рулевым управлением (РУ) на правой стороне равна 0.001. Какова вероятность того, что среди 2000 автомобилей окажется 3 автомобиля с РУ на правой стороне? Какова вероятность того, что их окажется не более трех? Для ДСВ – количества автомобилей с РУ на правой стороне построить ряд распределения и график функции распределения, найти МО и D. . Показать найденные вероятности на графике функции распределения. Задачу решить приближенно, пользуясь законом редких явлений (Распределение Пуассона).

	p x		x			x2
					e		,
6. Задана НСВ:						18			Найти b, МО, D, СКО для этой НСВ. Определить вероятность
			b	2		18
			b
								x 0
		0,				x 0

P(0<X<3 2 ). Построить график ФР и ПР и показать на каждом из графиков найденную вероятность. 7. В условиях задачи 6 найти плотность распределения случайной величины Y (X 1)2 .

9.ПР для СHСВ выражается формулой.

A, 2 x 2, 2 y 2 p(x, y)

0, иначе

Найти А,

определить

являются ли

и Y независимыми

СВ

или

нет.

Найти p(x) и

p(y),

F(x),

F(y), F(x,y).

Найти P 0 X 1

0 Y 1 .

10. ПР для НСВ выражается формулой

P(x)

(x 2)2

Является

ли

данная формула

ПР

для

НСВ?

Если «да»,

то

найти

вероятность

P 2 3 X 2 3 .

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019491.01 Кб45Задача к ИГА исправл..doc
#
15.05.201548.13 Кб38Задачи Кирилл Никульченков.doc
#
15.05.2015144 Кб87Задачи Анализ 2014-ответ.docx
#
15.05.2015337.92 Кб7Задачи к курсовой работе по статистике.doc
#
15.05.201535.33 Кб48ЗАДАЧИ КЕМЬ.doc
#
15.05.2015393.05 Кб111задачи по вариантам.pdf
#
21.08.2019134.66 Кб11Задачи по трудовому праву, каф гражд и трудовог...doc
#
15.05.2015154.11 Кб38Задачи ЭО с решением.doc
#
15.05.201519.55 Кб22заключение по результатам служебной проверки.docx
#
15.05.201538.14 Кб16заменить вопросы..docx
#
17.11.20181.37 Mб33Зарубин.doc