3. Что называют моментом силы, моментом импульса, моментом инерции? в каких единицах они измеряются?

Момент силы(синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, т.к в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Момент силы

Размерность - L²MT⁻²

Единицы измерения:

СИ - Ньютон-метр

Моме́нт и́мпульса(кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно - если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется.

Момент импульса

Размерность - L²MT⁻¹

Единицы измерения:

СИ - м²·кг·с⁻¹

СГС - см²·г·с⁻¹

Момент инерции— скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Момент инерции

Размерность - L²M

Единицы измерения:

СИ - кг·м²

СГС - г·cм²

4. Вывести основное уравнение динамики вращательного движения.

Согласно уравнению ()второй закон Ньютона для вращательного движения

По определению угловое ускорение и тогда это уравнение можно

переписать следующим образом

с учетом (5.9)

или

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу моментавсех внешних сил, действующих на это тело.

5. Сформулируйте теорему Гюйгенса-Штейнера.

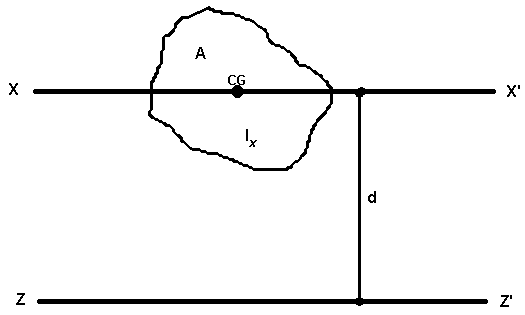
Теоре́ма Гю́йгенса — Ште́йнера, или простотеорема Штейнера(названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции телаIотносительно произвольной оси равен сумме момента инерции этого телаI^cотносительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы телаmна квадрат расстоянияdмежду осями:

I^new=I^c+md²,

где m— масса тела,d— расстояние между осями.

Например, Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью C) равен

Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен

J=J_C+md²,

где d— расстояние между искомой осью и осьюC. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формулеd=L/ 2:

Теорема Гюйнеса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор относительно произвольной точки из тензораотносительно центра масс. Пусть— смещение от центра масс, тогда

где

— вектор смещения от центра масс, а δ_ij— символ Кронекера.

Как видно, для диагональных элементов тензора (при i=j) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.

Иллюстрация теоремы для момента площади.