Метод трапеций

Метод трапеций

Подынтегральную функцию заменим на участке [х_j, х_j + h] полиномом первой степени P₁(х). Как и в методах прямоугольников, такая аппрокси­мация неоднозначна. Одним из возможных способов является проведение прямой через значения функции на границах интервала интегрирования (рис. 5.6). В этом случае приближенное значение интеграла определяется площадью трапеции

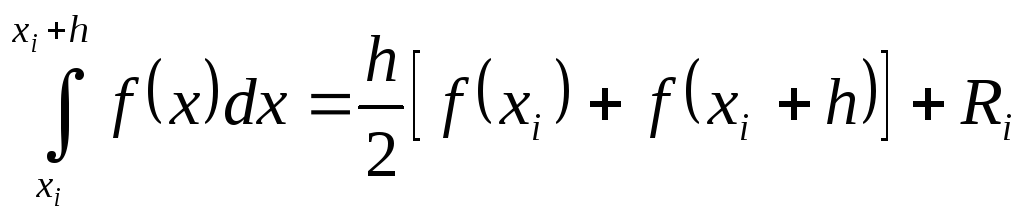(5.20)

Формула интегрирования для метода трапеций имеет вид:

(5.20а)

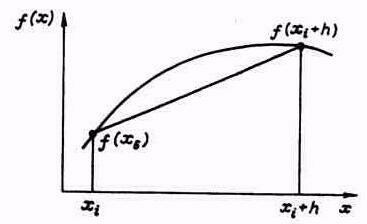
Рис. 5.6. Метод трапеций

Априорную погрешность R_i метода трапеций получим путем интегри­рования тейлоровского разложения подынтегральной функции около точки х_j

(5.21)

и интеграл

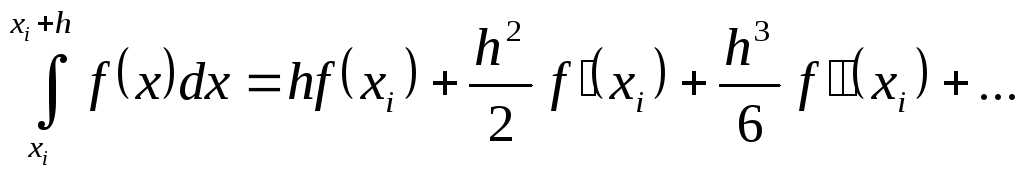(5.22)

С помощью разложения (5.21) вычислим подынтегральную функцию в точке x_j+h

откуда

(5.23)

Подставляя произведение (5.23) в выражение (5.22), получим

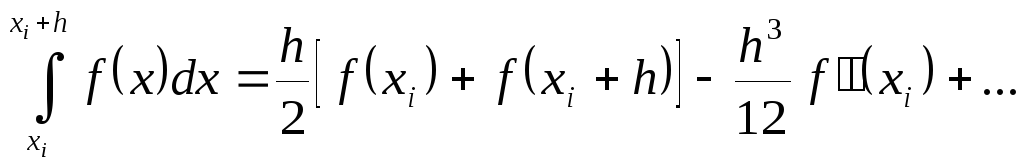
Следовательно, главный член погрешности метода трапеций на одном интервале будет

(5.24)

Если интегрирование проводится путем разбиения отрезка [x₀, х_n] на несколько интервалов, то общую погрешность получим суммированием частичных погрешностей (8.24)

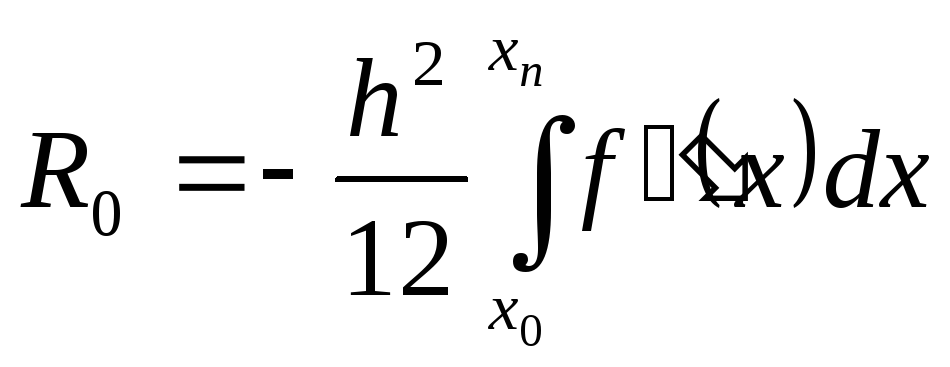(5.25)

Отсюда мы видим, что метод трапеций имеет второй порядок интегрирования. Это ожидаемый результат.

С другой стороны, метод средних прямоугольников также имеет второй порядок интегрирования. И как видно, из формул (5.7) и (5.25) погрешность метода трапеций даже больше в два раза больше по абсолютной вели­чине по сравнению с методом средних прямоугольников, хотя аппроксимация подынтегральной функции проводилась полиномом первой, а не нулевой степени. По-видимому, выбранный вариант аппроксимации подынтегральной функции прямой, проходящей через ее значения на границах, не является оптимальным. Задача выбора способа аппроксимации полиномом заданной степени с наименьшей возможной погрешностью была решена Гауссом, что привело к развитию целого класса методов (п. 5.8)

Поскольку метод трапеций и метод средних прямоугольников имеют одинаковый порядок интегрирования, то если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности.