Метод прямоугольников

Классификация методов

Ставится задача вычислить интеграл вида

(5.1)

где а и b - нижний и верхний пределы интегрирования; f(x) - непрерывная функция на отрезке [а, b].

Сущность большинства методов вычисления определенных интегралов состоит в замене подынтегральной функции f(x) аппроксимирующей функ­цией (x), для которой можно легко записать первообразную в элементарных функциях, т.е.

(5.2)

где S - приближенное значение интеграла; R - погрешность вычисления интеграла.

Методы прямоугольников

Рассмотрим сначала простейшие методы из класса методов Ньютона-Котеса, когда подынтегральную функцию f(x) на интервале интегрирования заменяем полиномом нулевой степени, т.е. константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке в интервале интегрирования. Приближенное значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая -аппроксимирующая константа. Отсюда происходит и название методов. Как будет показано ниже, из методов прямоугольников наименьшую по­грешность имеет метод средних прямоугольников, когда константу берем равной значению f(x) в средней точке интервала интегрирования [x_j-1, х_j] (рис. 52).

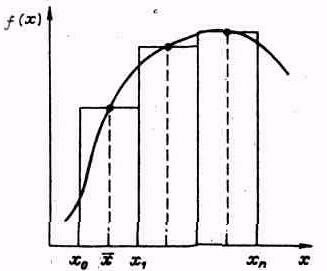
Рис. 5.2. Метод средних прямоуголь­ников

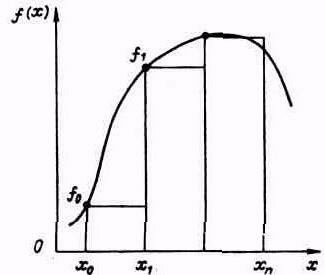
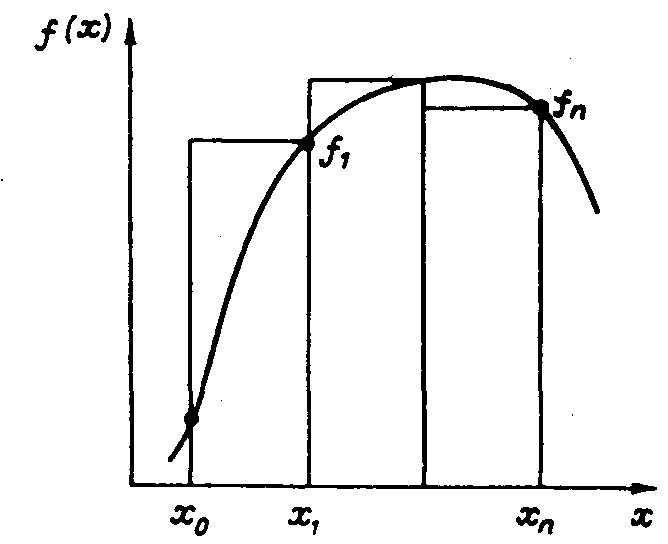
Рис. 5.3. Метод левых прямоугольников Рис. 5.4. Метод правых прямоуголь­ников

Формула интегрирования для i-го участка для метода левых прямоугольников:

Формула интегрирования для метода левых прямоугольников:

(5.2а)

Формула интегрирования для i-го участка для метода правых прямоугольников:

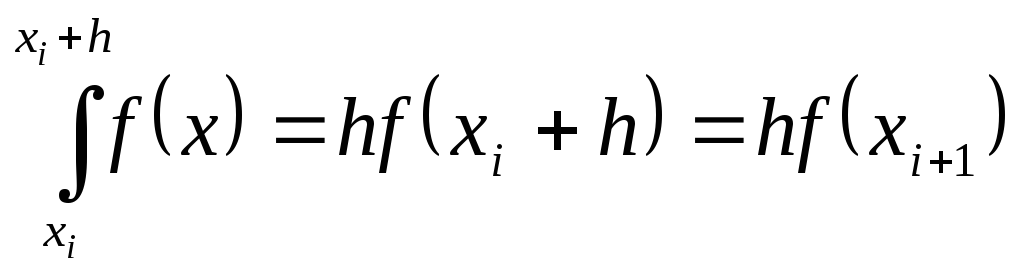
Формула интегрирования для метода правых прямоугольников:

(5.2б)

Формула интегрирования для i-го участка для метода средних прямоугольников:

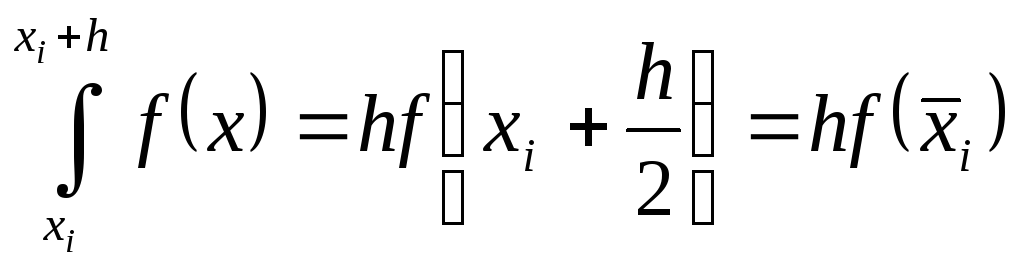
Формула интегрирования для метода средних прямоугольников:

(5.2с)

Методы левых (рис. 5.3) и правых прямоугольников (рис. 5.4), заменяющих интеграл нижней и верхней суммами Дарбу, имеют сравнительно высокую погрешность.

Запишем выражение для интеграла на интервале [х_j х_j+h], полученное методом средних прямоугольников.

(5.3)

где R_i=J_точн – J_прибл, и оценим погрешность R_i. Для этого разложим подынтегральную функцию f (х) в ряд Тейлора около средней точки

(5.4)

в малой окрестности точки х этот ряд с высокой точностью представляет функцию f(x) при небольшом количестве членов разложения. Поэтому, подставляя под интеграл вместо функции f(x) ее тейлоровское разложение (5.4) и, интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью

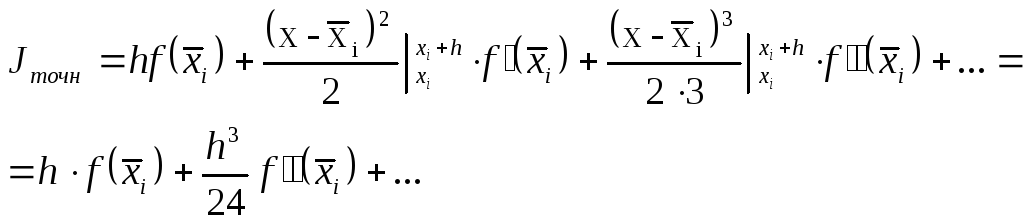(5.5)

При интегрировании и подстановке пределов получаем, что все интегралы от членов ряда (5.4), содержащих нечетные степени , обращаются в нуль.

Сравнивая соотношения (5.3) и (5.5), можно записать выражение для погрешности R_i. При малой величине шага интегрирования h основной вклад в погрешность R_i будет вносить первое слагаемое, которое называется главным членом погрешности R_0j вычисления интеграла на интервале [x_j, x_j+h]

(5.6)

Главный член полной погрешности для интеграла на всем интервале [x₀, х_n] определится путем суммирования погрешностей на каждом частич­ном интервале [x_j, x_j+h]

(5.7)

К последнему интегралу мы перешли, используя метод левых прямо­угольников для функции f"(х).

Формула (5.7) представляет собой теоретическую оценку погрешности вычисления интеграла методом средних прямоугольников, эта оценка является априорной, так как не требует знания значения вычисляемого интеграла. Оценка (5.7) не удобна для практического вычисления погрешности, но полезна для установления структуры главного члена погрешности. Степень шага h, которой пропорциональна величина R₀, называется поряд­ком метода интегрирования. Метод средних прямоугольников имеет второй порядок.

Аналогично проведем априорную оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора около точки х=х_j

(5.8)

Интегрируя разложение (5.8) почленно на интервале [х_j, х_j + h], получим

где первое слагаемое есть приближенное значение интеграла, вычисленное по методу левых прямоугольников, второе слагаемое является главным членом погрешности

(5.9)

На интервале [х₀, х_n] главный член погрешности интегрирования полу­чим суммированием частичных погрешностей (5.9)

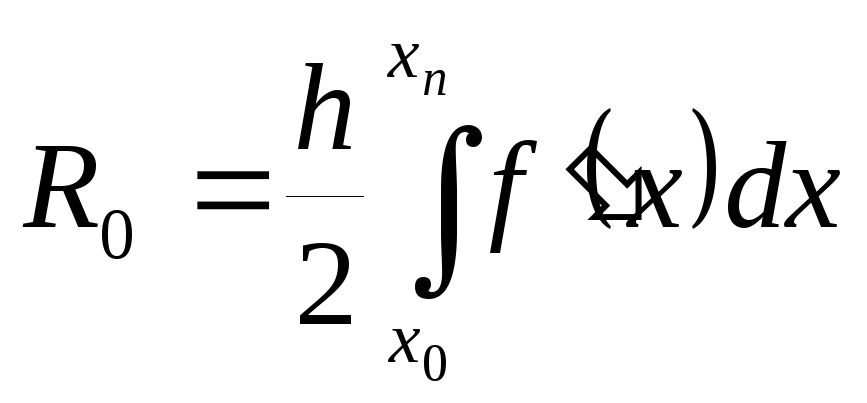(5.10)

Таким образом, метод левых прямоугольников имеет первый порядок; кроме того, погрешность будет больше по сравнению с методом средних и за счет интеграла от производной f'(x), и коэффициента в знаменателе (5.10). Обычно для большинства функций выполняется неравенство

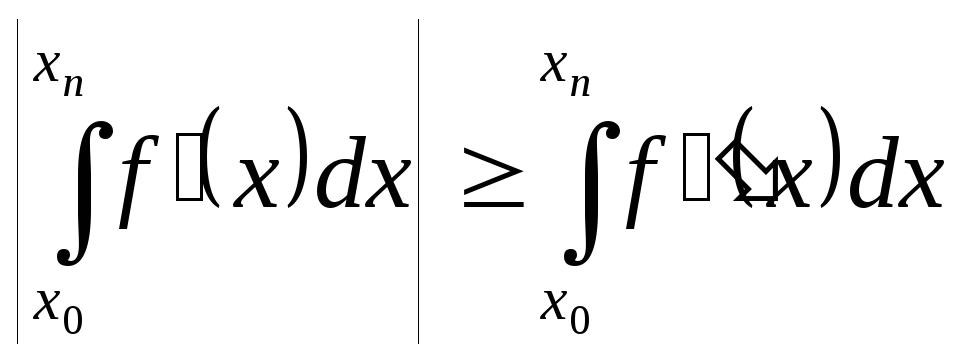
Однако, если подынтегральная функция f(x) определяется из экспери­мента в дискретном наборе узлов, то метод средних прямоугольников при­менить нельзя из-за отсутствия значений f(x) в средних точках х_j. В этом случае для интегрирования используются другие методы Ньютона-Котеса.