Метод Симпсона

Метод Симпсона

Будем заменять подынтегральную функцию f(x) на частичном интервале интерполяционным полиномом второй степени. Для этого число разбиений должно быть четным – 2n. Итак, рассмотрим интервал от x_i до x_i+2, заменим подынтегральную функцию f(x) на этом интервале интерполяционным полиномом второй степени Р₂(х) - параболой, проходящей через узлы х₀, х₁, x₂, (рис. 5.7), тогда

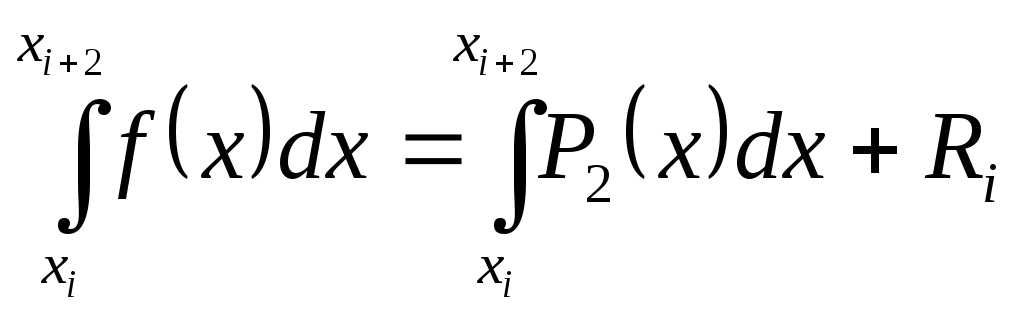
где R_i - погрешность вычисления интеграла.

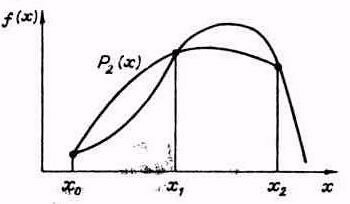
Рис. 5.7. Метод Симпсона

Для записи полинома Р₂(х) воспользуемся интерполяционной формулой Ньютона (3.6) для трех узлов

(5.27)

где

разделенные разности; h - расстояние между узлами.

Введем новую переменную z = х – x_i, тогда х = z + x_i и полином (5.27) принимает вид

(5.28)

Теперь вычислим интеграл от полинома (5.28)

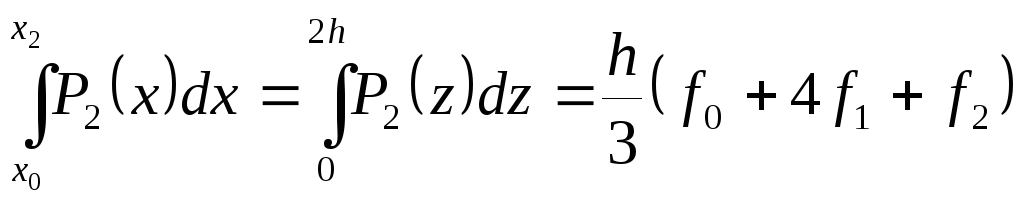(5.29)

Последнее соотношение называют квадратурной формулой Симпсона, или формулой парабол.

Окончательная формула интегрирования по методу Симпсона для интервала [a,b] имеет вид:

Формулу Симпсона можно получить и с помощью первой и второй формул Рунге, примененных к вычислению интеграла методом трапеций. Запишем два приближенных значения интеграла от функции f(x) на интервале [x₀, х₂] с шагами h и 2h по формуле трапеций (5.20).

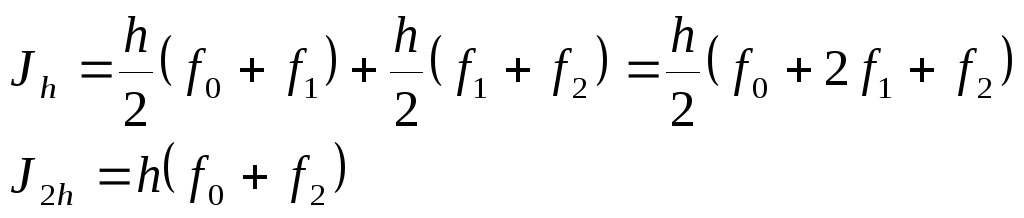(5.30)

Интегралы (5.30) подставим в формулы (5.15) и (5.16) и получим уточненное значение интеграла

которое совпадает с формулой Симпсона (5.29). Для оценки погрешности формулы Симпсона разложим подинтегральную функцию f(x) в ряд Тейлора около точки х₁ и проинтегрируем разложение почленно в интервале [x_i,x_i+2]

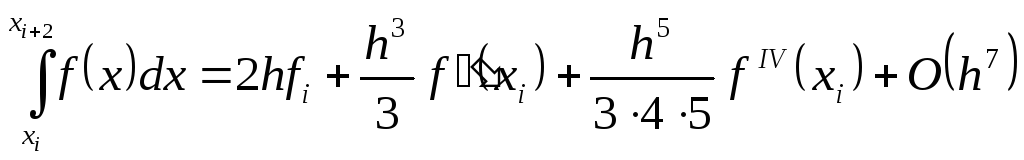(5.31)

Суммируя разложение около точки x₁ для функции f(x) в узлах x₀ и x₂ получим, что

тогда интеграл (5.31) принимает вид

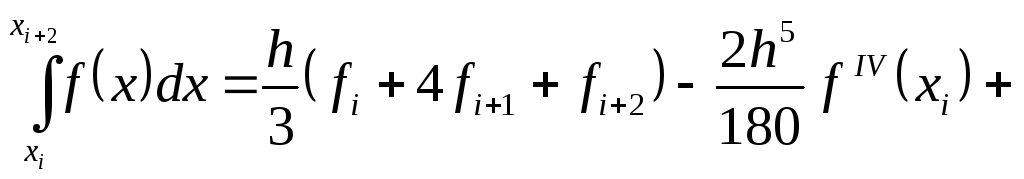
Первое слагаемое в правой части формулы (5.32) совпадает с формулой Симпсона, значит, второе слагаемое является главным членом погрешности для интеграла на интервале [x₀, x₂]

Если интеграл вычисляется на интервале [x₀, x_n] путем разбиения на четное число интервалов [x_j-1, x_j], на каждой паре которых приме­няется формула Симпсона для узлов x_j-1, x_j, x_j+1, то полная погрешность будет суммой правых частей соотношения (5.33). При малой величине шага h нa основании метода средних прямоугольников получим

тогда полная погрешность запишется в виде

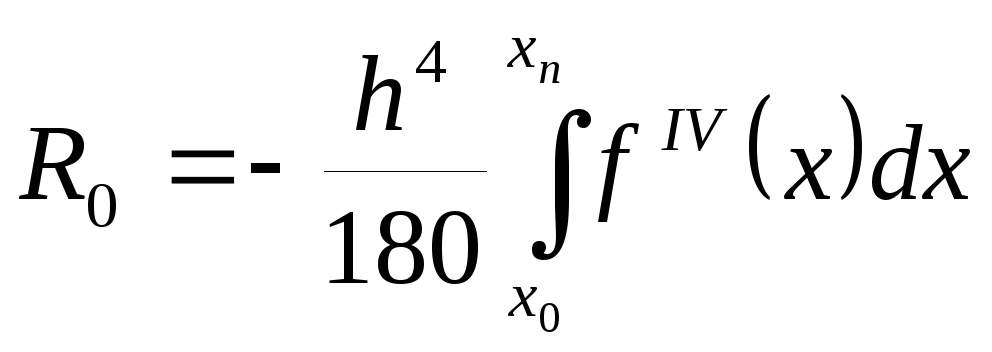(5.34)

Следовательно, формула Симпсона имеет четвертый порядок точности с очень малым численным коэффициентом в остаточном члене. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае методы второго порядка могут дать большую точность, чем метод Симпсона. Например [51], для функции f(x) = -25x⁴ + 45х² - 7 формула трапеций при n=2 для интеграла в пределах [-1, 1] дает точный результат, равный 4, тогда как по формуле Симпсона получим результат, не совпадающий даже по знаку (-8/3).