Вопрос 24. Логика в курсеинформатики.
Формы мышления
Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) от его содержания.
Логика — это наука о формах и способах мышления.
Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, высказывание и умозаключение.
Понятие. Понятие выделяет существенные признаки объекта, которые отличают его от других объектов. Объекты, объединенные понятием, образуют некоторое множество. Например, понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации и обладают монитором и клавиатурой. Даже по этому короткому описанию компьютер трудно спутать с другими объектами, например с механизмами, служащими для перемещения по дорогам и хранящимися в гаражах, которые объединяются понятием «автомобиль».
Понятие — это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие имеет две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов.
Например, содержание понятия «персональный компьютер» можно раскрыть следующим образом: «Персональный компьютер — это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя».
Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
Высказывание. Свое понимание окружающего мира человек формулирует в форме высказываний (суждений, утверждений). Высказывание строится на основе понятий и по форме является повествовательным предложением.
Высказывания могут быть выражены с помощью не только естественных языков, но и формальных. Например, высказывание на естественном языке имеет вид «Два умножить на два равно четырем», а на формальном, математическом языке оно записывается в виде: «2 • 2 = 4».
Об объектах можно судить верно или неверно, то есть высказывание может быть истинным или ложным. Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Примером истинного высказывания может служить следующее: «Процессор является устройством обработки информации».
Ложным высказывание будет в том случае, когда оно не соответствует реальной действительности, например: «Процессор является устройством печати».
Высказывание не может быть выражено повелительным или вопросительным предложением, так как оценка их истинности или ложности невозможна.
Конечно, иногда истинность того или иного высказывания является относительной. Истинность высказываний может зависеть от взглядов людей, от конкретных обстоятельств и так далее. Сегодня высказывание «На моем компьютере установлен самый современный процессор Pentium 4» истинно, но пройдет некоторое время, появится более мощный процессор, и данное высказывание станет ложным.
Высказывание - это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.
До сих пор мы рассматривали простые высказывания. На основании простых высказываний могут быть построены составные высказывания. Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединенных союзом «и».
Если истинность или ложность простых высказываний устанавливается в результате соглашения на основании здравого смысла, то истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний.
Приведенное выше составное высказывание истинно, так как истинны входящие в него простые высказывания.
Умозаключение. Умозаключения позволяют на основе известных фактов, выраженных в форме суждений (высказываний), получать заключение, то есть новое знание. Примером умозаключений могут быть геометрические доказательства.
Например, если мы имеем суждение «Все углы треугольника равны», то мы можем путем умозаключения доказать, что в этом случае справедливо суждение «Этот треугольник равносторонний ».
Умозаключение - это форма мышления, с помо- ^■0, щью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, еслиумозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае можно прийти к ложному умозаключению.
Вопросы для размышления
;'л
Какие существуют основные формы мышления?
В чем состоит разница между содержанием и объемом понятия?
Может ли быть высказывание выражено в форме вопросительного предложения?
Как определяется истинность или ложность простого высказывания? Составного высказывания?
Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.
В аргебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита. Рассмотрим два простых высказывания:
А = «Два умножить на два равно четырем».
В = «Два умножить на два равно пяти». Высказывания, как уже говорилось ранее, могут быть истинными или ложными. Истинному высказыванию соответствует значение логической переменной 1, а ложному — значение 0. В нашем случае первое высказывание истинно (А = 1), а второе ложно (В = 0).
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0).
В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.
Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Логическое умножение (конъюнкция)
s* f Объединение двух (или нескольких) высказыва-ний в одно с помощью союза «и» называется опера-
цией логического умножения или конъюнкцией.
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Так, из приведенных ниже четырех составных высказываний, образованных с помощью операции логического умножения, истинно только четвертое, так как в первых трех составных высказываниях хотя бы одно из простых высказываний ложно:
Компьютер как объект изучения является основной составной частью содержания школьного предмета, т.о. Основы информатики и вычислительной техники (ОИВТ), выполняя общеобразовательные функции, должна включать наиболее общезначимые сведения, которые раскрыли бы суть базовой науки информатики, вооружали учащихся ЗУН, необходимым выпускникам на современном этапе компьютеризации общества. 1
ИНФОРМАТИКА Пояснительная записка 5
Представление чисел в компьютере 11
Форматирование абзацев: 16
Графические объекты 17
Рисунки 17
Угринович Н.Д. - 8-9 класс - 12 часов. 18
ПРАВИЛА ЗАПИСИ ФУНКЦИЙ 19
Основные функции СУБД 22
Перейдем теперь от записи высказываний на естественном языке к их записи на формальном языке алгебры высказываний (алгебры логики). В ней операцию логического умножения (конъюнкцию) принято обозначать значком «&» либо «л». Образуем составное высказывание F, которое получится в результате конъюнкции двух простых высказываний:
F = А& В.
С точки зрения алгебры высказываний мы записали формулу функции логического умножения, аргументами которой являются логические переменные Aw. В, которые могут принимать значения «истина» (1) и «ложь» (0).
Сама функция логического умножения F также может принимать лишь два значения «истина» (1) и «ложь» (0). Значение логической функции можно определить с помощью таблицы истинности данной функции, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов (табл. 3.1).
Таблица 3.1. Таблица истинности функции логического умножения
|
А |
В |
F = А& В |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
По таблице истинности легко определить истинность составного высказывания, образованного с помощью операции логического умножения. Рассмотрим, например, составное высказывание «2-2 = 4иЗ-3 = 10». Первое простое высказывание истинно (А = 1), а второе высказывание ложно (Б = 0), по таблице определяем, что логическая функция принимает значение ложь (F — 0), то есть данное составное высказывание ложно.
Логическое сложение (дизъюнкция)
Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией.
j Составное высказывание, образованное в резуль- тате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Так, из приведенных ниже четырех составных высказываний, образованных с помощью операции логического сложения, ложно только первое, так как в последних трех составных высказываниях хотя бы одно из простых высказываний истинно:
Компьютер как объект изучения является основной составной частью содержания школьного предмета, т.о. Основы информатики и вычислительной техники (ОИВТ), выполняя общеобразовательные функции, должна включать наиболее общезначимые сведения, которые раскрыли бы суть базовой науки информатики, вооружали учащихся ЗУН, необходимым выпускникам на современном этапе компьютеризации общества. 1
ИНФОРМАТИКА Пояснительная записка 5
Представление чисел в компьютере 11
Форматирование абзацев: 16
Графические объекты 17
Рисунки 17
Угринович Н.Д. - 8-9 класс - 12 часов. 18
ПРАВИЛА ЗАПИСИ ФУНКЦИЙ 19
Основные функции СУБД 22
Запишем теперь операцию логического сложения на формальном языке алгебры логики. Операцию логического сложения (дизъюнкцию) принято обозначать либо значком «V», либо знаком сложения «+». Образуем составное высказывание F, которое получится в результате дизъюнкции двух простых высказываний:
F = Av В.
С точки зрения алгебры высказываний мы записали формулу функции логического сложения, аргументами которой являются логические переменные А я В. Значение логической функции можно определить с помощью таблицы истинности данной функции, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов (табл. 3.2).
Таблица 3.2. Таблица истинности функции логического сложения
|
А |
В |
F = AvB |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
По таблице истинности легко определить истинность составного высказывания, образованного с помощью операции логического сложения. Рассмотрим, например, составное высказывание «2-2 = 4 или 3 • 3 = 10». Первое простое высказывание истинно (А = 1), а второе высказывание ложно (Б = 0), по таблице определяем, что логическая функция принимает значение истина (F = 1), то есть данное составное высказывание истинно.
3.2.3. Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.
Ы
а
Операцию логического отрицания (инверсию) над логиче- ским_высказыванием А в алгебре логики принято обозначать А. Образуем высказывание F, являющееся логическим отрицанием А:
F = А.
Истинность такого высказывания задается таблицей истинности функции логического отрицания (табл. 3.3).
Таблица 3.3. Таблица истинности функции логического отрицания
|
А |
F=A |
|
0 |
1 |
|
1 |
0 |
Истинность высказывания, образованного с помощью операции логического отрицания, можно легко определить с помощью таблицы истинности. Например, высказывание «Два умножить на два не равно четырем» ложно (А = 0), а полученное из него в результате логического отрицания высказывание «Два умножить на два равно четырем» истинно (F = 1).
Составить составное высказывание, содержащее операции логического умножения, сложения и отрицания. Определить его истинность.
Логические выражения и таблицы истинности
Логические выражения. Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
5—2645
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание «(2 -2 = 5 или 2-2 = 4) и (2- 2*5 или 2 • 2 * 4)». Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2 • 2 = 5» — ложно (0),
В = «2 • 2 = 4» — истинно (1).
Тогда составное высказывание можно записать в следующей форме:
«(А или В) и (.А или В)».
Теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения: инверсия, конъюнкция, дизъюнкция. Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (A v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В)&(А v Б) = (0 v 1)&(1 v 0) = 1 & 1 = 1.
Таблицы истинности. Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во-первых, необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2”.
В нашем случае логическая функция F = (AvB)&(AvB) имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4.
Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операций — пяти, то есть количество столбцов таблицы истинности равно семи.
В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных.
В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности (табл. 3.4). Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
Таблица 3.4. Таблица истинности логической функции F= (A v Б)&(4 v В)
|
А |
В |
AvB |
А |
в |
AvB |
(AvB)MAvB) |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
о I |
Равносильные логические выражения. Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения А& В и AvB равносильны. Построим сначала таблицу истинности логического выражения А& В (табл. 3.5).
Таблица 3.5. Таблица истинности логического выражения А& В
|
А |
В |
А |
В |
А&В |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
Теперь построим таблицу истинности логического выражения AvB (табл. 3.6).
Таблица 3.6. Таблица истинности логического выражения AvB
|
А |
В |
AvB |
AvB |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:
А&В = AvB.
Вопросы для размышления
Что содержат таблицы истинности и каков порядок их построения?
Какие логические выражения называются равносильными?
Задания
^ wife»’'
Записать составное высказывание «(2 •2 = 4и3-3 = 9) или (2-2*4иЗ З* 9)» в форме логического выражения. Построить таблицу истинности.
Доказать, используя таблицы истинности, что логические выражения A v В и А&В равносильны.
Логические функции
Любое составное высказывание можно рассматривать как логическую функцию F(XV Х2, ..., Хп), аргументами которой являются логические переменные Xv Х2, ..., Хп (простые высказывания). Сама функция и аргументы могут принимать только два различных значения: «истина» (1) и «ложь» (0).
Выше были рассмотрены функции двух аргументов: логическое умножение F(A,B) = А&В, логическое сложение F(A,B) = AvB, а также логическое отрицание F(A) = А, в котором значение второго аргумента можно считать равным нулю.
Каждая логическая функция двух аргументов имеет четыре возможных набора значений аргументов. По формуле (2.1) мы можем определить, какое количество различных логических функций двух аргументов может существовать:
N = 24 = 16.
Таким образом, существует 16 различных логических функций двух аргументов, каждая из которых задается своей таблицей истинности (табл. 3.7).
Таблица 3.7. Таблицы истинности логических функций двух аргументов
|
Аргу менты |
Логические функции | ||||||||||||||||
|
А |
В |
|
|
F3 |
|
|
|
|
|
|
|
^11 |
^12 |
|
F14 |
|
^16 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Легко заметить, что здесь логическая функция F2 является функцией логического умножения, F8 — функцией логического сложения, F13 — функцией логического отрицания для аргумента А и Fn — функцией логического отрицания для аргумента В.
В обыденной и научной речи кроме базовых логических связок «и», «или», «не» используются и некоторые другие: «если... то...», «... тогда и только тогда, когда...» и др. Некоторые из них имеют свое название и свой символ, и им соответствуют определенные логические функции.
Логическое следование (импликация). Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если..., то...».
Логическая операция импликации «если А, то В», обозначается А —» В и выражается с помощью логической функции Fu, которая задается соответствующей таблицей истинности (табл. 3.8).
Таблица 3.8. Таблица истинности логической функции «импликация»
|
IА |
в |
f14 = a->b |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
I 1 |
1 |
1 |
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Например, высказывание «Если число делится на 10, то оно делится на 5» истинно, так как истинны и первое высказывание (предпосылка), и второе высказывание (вывод).
Высказывание «Если число делится на 10, то оно делится на 3» ложно, так как из истинной предпосылки делается ложный вывод.
Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание (предпосылка) ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно.
В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базовым: логическому умножению, логическому сложению и логическому отрицанию.
Докажем методом сравнения таблиц истинности (табл. 3.8 и 3.9), что операция импликации А -> В равносильна логическому выражению AvB.
Таблица 3.9. Таблица истинности логического выражения AvB
|
А |
В |
А |
A vВ |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
Таблицы истинности совпадают, что и требовалось доказать.
Логическое равенство (эквивалентность). Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «... тогда и только тогда, когда ...».
Логическая операция эквивалентности «А тогда и только тогда, когда В» обозначается А-В и выражается с помощью логической функции F10, которая задается соответствующей таблицей истинности (табл. 3.10).
Таблица 3.10. Таблица истинности логической функции эквивалентности
|
А |
В |
FW |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Рассмотрим, например, два высказывания: А = «Компьютер может производить вычисления» и В = «Компьютер включен». Составное высказывание, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны:
«Компьютер может производить вычисления тогда и только тогда, когда компьютер включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».
Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно высказывание истинно, а другое — ложно:
«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».
«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».
Вопросы для размышления
Какое количество логических функций двух аргументов существует и почему?
Какие логические функции двух аргументов имеют свои названия?
Какое существует количество логических функций трех аргументов?
Доказать, используя таблицы истинности, что операция эквивалентности А -В равносильна логическому выражению:
(Л v В) & (A v В).
Логические законы и правила преобразования логических выражений
Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.
Закон тождества. Всякое высказывание тождественно самому себе:
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно:
Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»:
А
= А
Законы де Моргана.
A v В = Я & В А & В = A v В
Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.
Закон коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:
|
Логическое умножение |
Логическое сложение I |
|
А & В= В& А |
A v В = A v В I |
а
|
Логическое умножение |
Логическое сложение |
|
(А & В) & С = А & (В & С) |
(A v В) v С = A v (В v С) |
Закон дистрибутивности. В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:
|
Дистрибутивность умножения относительно сложения |
Дистрибутивность сложения относительно умножения |
|
ab+ ас = а(Ы-с) — в алгебре (A&B)v[A&C)=A&{BvC) |
(A v В) & (A v С) = A v (В & С) |
Рассмотрим в качестве примера применения законов логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:
(А & В) v (А & В).
Воспользуемся законом дистрибутивности и вынесем за скобки А:
(А & В) v (А & В) = А & (В v В).
По закону исключенного третьего В v В =1, следовательно:
А& (В vB) = А & 1 = А.
Доказать справедливость первого A v В = А & В и второго
А & В = A v В законов де Моргана, используя таблицы истинности.
Упростить логические выражения:
а) (A v А) & В; _
б) А & (A v Б) & (В v В).
Решение логических задач
Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, то есть записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.
Условие задачи. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории — табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.
Решение задачи. Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:
А = «В первой аудитории находится кабинет информатики»; В = «Во второй аудитории находится кабинет информатики».
Отрицания этих высказываний:
А = «В первой аудитории находится кабинет физики»;
В = «Во второй аудитории находится кабинет физики».
Высказывание, содержащееся на табличке на двери первой аудитории, соответствует логическому выражению:
X = AvB.
Высказывание, содержащееся на табличке на двери второй аудитории, соответствует логическому выражению:
У = А.
Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего записывается следующим образом:
(X & У) v(X & У) = 1.
Подставим вместо X и У соответствующие формулы:
(X & У) v (X & У) = ((Л v В) & A) v ((A v В) & I).
Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:
(A v В) &А = А & A v В& А.
В соответствии с законом непротиворечия:
А & A v В& А = 0 v В & А.
Упростим теперь второе слагаемое. В соответствии с первым законом де Мо_ргана и законом двойного отрицания:
(A v В) & А = А&В & А = А & А & Ъ.
В соответствии с законом непротиворечия: А&А&В=0&В = 0.
В результате получаем:
(О v В& A) v 0 = В & А.
Полученное логическое выражение оказалось простым и поэтому его можно проанализировать без построения таблицы истинности^ Для того чтобы выполнялось равенство В&А = 1,ВиА должны быть равны 1, то есть соответствующие им высказывания истинны.
Ответ: В первой аудитории находится кабинет физики, а во второй — кабинет информатики.
В процессе составления расписания уроков учителя высказали свои пожелания. Учитель математики высказал пожелание проводить первый или второй урок, учитель информатики — первый и третий, а учитель физики — второй или третий урок. Сколько существует возможных вариантов расписания и каковы они?
Логические основы устройства компьютера
Базовые логические элементы
Базовые логические элементы реализуют рассмотренные выше три основные логические операции:
логический элемент «И» — логическое умножение;
логический элемент «ИЛИ» — логическое сложение;
логический элемент «НЕ» — инверсию.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс — логический смысл сигнала — 1, нет импульса —На входы логического элемента поступают сигналы-зна-чения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
А
(0,0,1,1)
В
(0,1,0,1)
F
(0,0,0,1)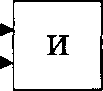
Рис. 3.1
Логический элемент «И»
Логический элемент «ИЛИ». На входы А и В логического элемента (рис. 3.2) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
F
(0,1,1,1)
А
(0,0,1,1)
В
(0,1,0,1)
Логический элемент «НЕ». На вход А логического элемента (рис. 3.3) подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.
|
Рис. 3.3 Логический элемент «НЕ» |
А (0,1) |
НЕ |
F (1,0) |
|
|
|
|
Сумматор двоичных чисел
В целях максимального упрощения работы компьютера все многообразие математических операций в процессоре сводится к сложению двоичных чисел. Поэтому главной частью процессора являются сумматоры, которые как раз и обеспечивают такое сложение.
Полусумматор. Вспомним, что при сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд. Введем обозначения слагаемых (А, В), переноса (Р) и суммы (S). Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом:
|
Слагаемые |
Перенос |
Сумма | |
|
А |
В |
Р |
S |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Из этой таблицы сразу видно, что перенос можно реализовать с помощью операции логического умножения:
Р =А& В.
Получим теперь формулу для вычисления суммы. Значения суммы близки к результату операции логического сложения (кроме случая, когда на входы подаются две единицы, а на выходе должен получиться нуль).
Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить следующее логическое выражение:
S = (A v В) & (А & В).
Построим таблицу истинности для данного логического выражения и убедимся в правильности нашего предположения (табл. 3.11).
Таблица 3.11. Таблица истинности логической функции F= (AvB)&(A&B)
|
А |
В |
AvB |
А & В |
А & В |
(АчВЩА&В) |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему сложения одноразрядных двоичных чисел.
По логической формуле переноса легко определить, что для получения переноса необходимо использовать логический элемент «И».
Анализ логической формулы для суммы показывает, что на выходе должен стоять элемент логического умножения «И», который имеет два входа. На один из входов надо подать результат логического сложения исходных величин Avi В, то есть на него должен подаваться сигнал с элемента логического сложения «ИЛИ».
На второй вход требуется подать результат инвертированного логического умножения исходных сигналов (А & В), то есть на второй вход должен подаваться сигнал с элемента «НЕ», на вход которого должен поступать сигнал с элемента логического умножения «И» (рис. 3.4).
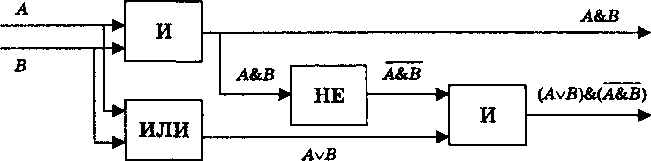
Рис. 3.4. Полусумматор двоичных чисел
Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Полный одноразрядный сумматор. Полный одноразрядный сумматор должен иметь три входа: А, В — слагаемые и Р0 - перенос из младшего разряда и два выхода: сумму S и перенос Р. Таблица сложения в этом случае будет иметь следующий вид:
|
Слагаемые |
Перенос из младшего разряда |
Перенос |
Сумма | |
|
А |
В |
Ро |
Р |
S |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Идея построения полного сумматора точно такая же, как и полусумматора. Из таблицы сложения видно, что перенос (логическая переменная Р) принимает значение 1 тогда, когда хотя бы две входные логические переменные одновременно принимают значение 1. Таким образом, перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных (А, В, Р0). Формула переноса получает следующий вид:
Р = (А&В) v (A &P0)v (В & Р0).
Для получения значения суммы (логическая переменная S) необходимо результат логического сложения входных переменных (А, В, Р0) умножить на инвертированный перенос Р:
S = (AvBvP0)&P.
Данное логическое выражение дает правильные значения суммы во всех случаях, кроме одного, когда на все входные логические переменные принимают значение 1. Действительно:
Р - (1 & 1) v (1 & 1) v (1 & 1) = 1;
S = (lvlvl)&P = 1 & 0 = 0.
Для получения правильного значения суммы (для данного случая переменная S должна принимать значение 1) необходимо сложить полученное выше выражение для суммы с результатом логического умножения входных переменных (А, В, PQ). В результате логическое выражение для вычисления суммы в полном сумматоре принимает следующий вид:
S = (A v В v Р0) & Р0 v (А & В & Р0).
Многоразрядный сумматор. Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, при-' чем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.
Триггер
Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора является триггер. Это устройство позволяет запоминать, хранить и считывать информацию (каждый триггер может хранить 1 бит информации).
Триггер можно построить из двух логических элементов «ИЛИ» и двух элементов «НЕ» (рис. 3.5).
Рис. 3.5
Триггер
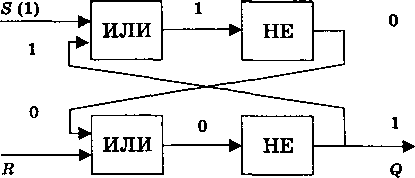
В обычном состоянии на входы триггера подан сигнал О, и триггер хранит 0. Для записи 1 на вход S (установочный) подается сигнал 1. Последовательно рассмотрев прохождение сигнала по схеме, видим, что триггер переходит в это состояние и будет устойчиво находиться в нем и после того, как сигнал на входе S исчезнет. Триггер запомнил 1, то есть с выхода триггера Q можно считать 1.
Для того чтобы сбросить информацию и подготовиться к приему новой, подается сигнал 1 на вход R (сброс), после чего триггер возвратится к исходному «нулевому» состоянию.