

Математическое программирование
Задача 1
Кондитерская фабрика для производства двух видов карамели К1 и К2 использует три вида основного сырья: сахар, патоку, фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т. карамели К1 – 0,5; 0,4; 0,1 соответственно, на производство 1 т. карамели К2 – 0,8; 0,3; 0,1 соответственно. Общий запас сахара – 80 т., патоки – 60 т., фруктового пюре – 12 т. Прибыль от
реализации 1 т. карамели К1 составляет 108 тыс. р., а |
1 т. карамели К2 – |
|||||
112 тыс. р. Найти |
оптимальный план |
производства карамели, достигающий |
||||
максимальную прибыль: |
|
|
|
|||
а) |
записать математическую модель задачи; |
|
|
|||
б) |
решить задачу графическим методом; |
|
|
|||
в) |
решить задачу симплекс-методом; |
|
|
|
||
г) |
к исходной задаче записать двойственную и найти ее решение, используя |
|||||
соотношения двойственности и решение исходной задачи. |
|
|
||||
Решение |
|
|
|
|
|
|
|
Примем, что план фабрики определяется количеством тонн произведенной |
|||||
карамели каждого вида. |
|
|
|
|||
|
Представим исходную информацию в таблице: |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Затраты сырья на производство 1т. |
|
||
|
Виды сырья |
|
продукции |
|
|
Запас сырья, т. |
|
|
|
К1 |
К2 |
|
|
|
|
|
|
|
|
|
|
Сахар |
|
0,5 |
0,8 |
|
80 |
|
|
|
|
|
|
|
|
Патока |
|
0,4 |
0,3 |
|
60 |
|
|
|
|
|
|
|
|
Фруктовое пюре |
|
0,1 |
0,1 |
|
12 |
|
|
|
|
|
|
|
|
Доход, тыс. р. |
|
108 |
112 |
|
|
|
|
|
|
|
|
|
а) Построение математической модели задачи |
|
|
|
|||||
Пусть теперь |
x1 – |
количество (т.) карамели вида К1, а |
x2 |
– |
||||
количество (т.) |
карамели |
вида |
К2. |
Тогда |
компоненты |
x1 |
и |
x 2 |
производственного |
плана |
(x1 ; x2 ) |
, |
очевидно, |
должны |
удовлетворять |
||
следующим условиям-ограничениям по затратам cырья:
0,5 x1+0,8 x2 80 ;
0,4 x1+0,3 x2 60 ; 0,1 x1+0,1 x2 12 ; x1 0, x2 0.
С другой стороны, пара x1 , x2 , удовлетворяющая этим условиям, может рассматриваться как некоторый вариант производственного плана.
Требуется найти план, приносящий кондитерской фабрике наибольший доход, т. е. Найти допустимый план, для которого функция
f (x 1, x2)=108 x1+112 x2
принимает наибольшее значение.
Итак, пришли к следующей задаче ЛП: найти max(108 x1+112 x2) при условиях
0,5 x1+0,8 x2 80 ;
0,4 x1+0,3 x2 60 ; 0,1 x1+0,1 x2 12 ; x1 0, x2 0.
б) Графическое решение задачи
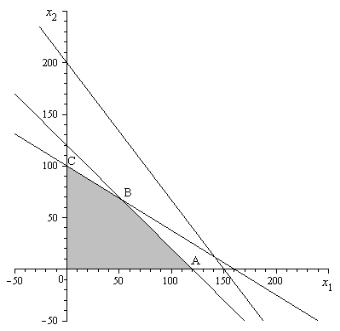
В плоскости строим декартову систему координат с осями x1 и x2 . Далее строим решение системы неравенств-ограничений:
0,5 x1+0,8 x2 80 ;
0,4 x1+0,3 x2 60 ; 0,1 x1+0,1 x2 12 ; x1 0, x2 0.
Точки, удовлетворяющие системе неравенств-ограничений, образуют многоугольник OABC.
Выберем некоторую точку M из данного многоугольника, точка (0 ;50)
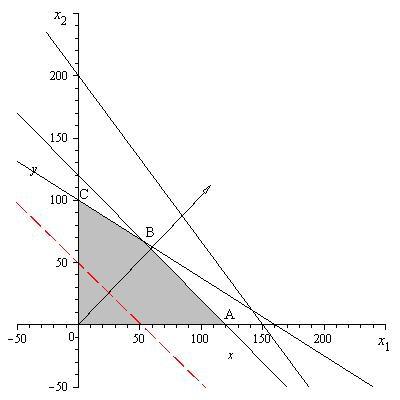
вполне подойдет. Строим вектор c(108;112) . Проводим через точку M прямую π , перпендикулярную вектору с . Далее перемещаем эту прямую параллельно самой себе по направлению вектора с , пока она не займет относительно области OABC крайнего верхнего положения. Это произойдет, когда она пройдет через точку B.
Таким образом, оптимальное решение определяется координатами точки B. Так как в точке B пересекаются прямые, отвечающие первому и третьему неравенствам, то ее координаты находим из решения системы уравнений
0,5 x1+0,8 x2=80;
0,1 x1+0,1 x2=12.
x1=1603 ; x2= 2003 .
Следовательно, кондитерская фабрика должна производить 160/3 т. карамели вида К1 и 200/3 т. карамели вида К2, при этом ее доход будет составлять
108 1603 +112 2003 =396803 ≈13226,667 тыс.рублей.
в) Решение задачи симплекс-методом
Прежде всего приведем задачу к каноническому виду, вводя в каждое основное неравенство свою дополнительную переменную yi при ограничениях:

0,5 x1+0,8 x2+ y1=80 ;
0,4 x1+0,3 x2+ y2=60 ; 0,1 x1+0,1 x2+ y3=12 ;
x1 0, x2 0, y1 0, y2 0, y3 0.
Найти max(108 x1+112 x2+0 y1+0 y2+0 y3) .
Отметим, что правые части системы уравнений неотрицательны, система
уравнений является разрешенной относительно переменных |
y1, y2, y3 , |
которые могут считаться базисными переменными начального базисного решения x1=0, x2 =0, y1=80, y2=60, y3=12 . Отметим так же, что функция f не содержит базисных переменных. Значение функции f для начального
решения f ( X нач)=0 . Для составления начальной симплекс |
таблицы мы |
выполнили все условия. В процессе дальнейших преобразований |
возможны два |
случая. Если в симплекс таблице, на каком-то шаге, мы получим строку f , состоящую из неотрицательных элементов – задача решена, мы нашли оптимальное решение. В противном случае – функция не является ограниченной.
Шаг 1
За ведущий выберем столбец 2 , так как -112 – наименьший элемент в f - строке. Элемент f строки, принадлежащий столбцу свободных членов не рассматриваем. За ведущую выберем строку 1, так как отношение свободного члена к соответствующему элементу выбранного столбца для 1 строки является наименьшим. Отметим, что отношение мы вычисляем только для положительных элементов столбца 2.
Базисные |
x1 |
|
x2 |
|
|
y1 |
y2 |
y3 |
Свободные |
Отношение |
переменные |
|
|
|
|
|
|
|
|
члены |
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
0,5 |
|
|
|
1 |
|
0 |
0 |
80 |
100 |
0,8 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
y2 |
0,4 |
|
0,3 |
|
0 |
|
1 |
0 |
60 |
200 |
|
|
|
|
|
|
|
|
|
|
|
y3 |
0,1 |
|
0,1 |
|
0 |
|
0 |
1 |
12 |
120 |
|
|
|
|
|
|
|
|
|
|
|
f |
-108 |
|
-112 |
|
0 |
|
0 |
0 |
0 |
~ |
|
|
|
|
|
|
|
|
|||
Разделим элементы строки 1 на 0,8. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Базисные |
x1 |
|
x2 |
|
|
y1 |
y2 |
y3 |
Свободные |
Отношение |
переменные |
|
|
|
|
|
|
|
|
члены |
|
y1 |
5 |
|
|
|
|
5 |
0 |
0 |
100 |
100 |
1 |
|
|
||||||||
|
8 |
|
|
|
|
4 |
|
|
|
|
y2 |
0,4 |
|
0,3 |
|
0 |
|
1 |
0 |
60 |
200 |
|
|
|
|
|
|
|
|
|
|
|
y3 |
0,1 |
|
0,1 |
|
0 |
|
0 |
1 |
12 |
120 |
|
|
|
|
|
|
|
|
|
|
|
f |
-108 |
|
-112 |
|
0 |
|
0 |
0 |
0 |
~ |
|
|
|
|
|
|
|
|
|
|
|

От элементов строки 2 отнимаем соответствующие элементы строки 1, умноженные на 0,3. От элементов строки 3 отнимаем соответствующие элементы строки 1, умноженные на 0,1. От элементов строки f отнимаем соответствующие элементы строки 1, умноженные на -112.
Базисные |
x1 |
x2 |
y1 |
y2 |
y3 |
Свободные члены |
переменные |
|
|
|
|
|
|
x2 |
5 |
|
1 |
5 |
|
0 |
0 |
100 |
|
|
8 |
|
|
4 |
|
|
|
|
|
y2 |
17 |
|
0 |
− |
3 |
1 |
0 |
30 |
|
|
80 |
|
|
8 |
|
|
|
||
y3 |
3 |
|
0 |
− |
1 |
0 |
1 |
2 |
|
|
|
80 |
|
|
8 |
|
|
|
|
f |
-38 |
|
0 |
140 |
0 |
0 |
11200 |
||
|
|
|
|
|
|
|
|
|
|
X 1 =(0, |
100, |
0, 30, |
2) , |
|
|
|
|
||
f =11200+38 x1−140 x2=11200. |
|
|
|
|
|||||
Значение функции |
f для данного решения равно 11200. |
|
|||||||
Шаг 2 |
|
|
|
|
|
|
|
|
|
За ведущий выберем столбец 1 , так как -38 наименьший элемент в f - строке. Элемент f строки, принадлежащий столбцу свободных членов не рассматриваем. За ведущую выберем строку 3, так как отношение свободного члена к соответствующему элементу выбранного столбца для 3 строки является наименьшим. Отметим, что отношение мы вычисляем только для положительных элементов столбца 1.
Базисные |
x1 |
x2 |
y1 |
y2 |
y3 |
Свободные отношение |
переменные |
|
|
|
|
|
члены |
x2 |
5 |
|
1 |
5 |
|
0 |
0 |
100 |
160 |
||
|
8 |
|
|
4 |
|
|
|
|
|
|
|
y2 |
17 |
|
0 |
− |
3 |
1 |
0 |
30 |
2400 |
||
|
80 |
|
|
8 |
|
|
|
|
17 |
||
y3 |
|
|
|
0 |
|
1 |
0 |
1 |
2 |
160 |
|
3 |
|
− |
|||||||||
|
|
80 |
|
|
8 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
-38 |
|
0 |
140 |
0 |
0 |
11200 |
~ |
|||
|
|
|
|
|
|
|
|
|
|||
Разделим элементы строки 3 на |
|
3 . |
|
|
|
||||||
|
|
|
|
|
|
|
80 |
|
|
|
|
