
ТВ случайные события Заочное
.pdf
Пример.
В ателье имеются 5 плейеров, выпущенных заводом B,
10 плейеров – заводом C, 15 плейеров – заводом D. Вероятность того, что плейеры, выпущенные заводами B, С, D, выдержат гарантийный срок службы, соответственно равны 0,8, 0,85 и 0,9.
Найти вероятность того, что взятый наудачу плейер выдержит гарантийный срок службы.
Решение:
Событие А = {плейер выдержит гарантийный срок службы}, Гипотеза H1 = {плейер выпущен заводом В},
Гипотеза H2 = {плейер выпущен заводом С},
Гипотеза H3 = {плейер выпущен заводом D}.

P H |
|
|
5 |
|
1 |
; |
|
|||
|
|
|
|
|||||||
1 |
|
30 |
|
|
6 |
|
|
|||
|
|
|
|
|
|
|
||||
P H |
|
|
|
10 |
|
1 |
; |
|||
2 |
30 |
3 |
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
P H |
|
15 |
|
1 |
; |
|||||
|
|
|
||||||||
|
|
3 |
|
30 |
|
|
2 |
|
||
|
|
|
|
|
|
|
||||
P |
A |
H |
|
1 |
|
P |
A |
H |
|
2 |
A |
P |
|
H |
|
3 |
|
=0,8
=0,85
=0,9
По формуле полной вероятности
P A P H |
P |
A P H |
2 |
P |
|
|
A P H |
P |
A |
|||||
|
|
1 |
H |
1 |
|
|
|
H |
2 |
3 |
H |
3 |
||
|
|
|
|
|
|
|
|
|
|
|
||||
= |
1 |
0,8 + |
1 |
0,85 + |
1 |
0,9 ≈ 0,867 |
||||||||
|
|
|
|
|||||||||||
6 |
3 |
2 |
||||||||||||

Пример.
Литьё в болванках поступает из двух заготовительных цехов: 70% из первого цеха, 30% из второго цеха. Литьё первого цеха имеет 10% брака, второго – 20% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность её изготовления первым цехом?
Решение: Событие А ={болванка без дефекта}. Гипотеза H1 – болванка изготовлена первым цехом, Гипотеза H2 – болванка изготовлена вторым цехом,
Литьё первого цеха имеет 10% брака, следовательно, 90% болванок, изготовленных первым цехом, не имеют дефекта и
1 =0,9.
Литьё второго цеха имеет 20% брака, следовательно, 80% болванок, изготовленных вторым цехом, не имеют дефекта и
2 =0,8.
Необходимо найти PA H1 .

По формуле Бейеса
|
H |
|
P H |
P |
|
A |
|
P H |
P |
A |
|
|
|
||
P |
1 |
H |
1 |
|
|
|
1 |
H |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
A |
1 |
|
P A |
|
|
P H |
P |
A P H |
|
P |
A |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
H |
1 |
|
|
2 |
H |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0,7 0,9 |
|
0,63 |
|
0,63 |
0,724 |
|
0,9 0,3 0,8 |
|
0,24 |
|
||||
0,7 |
|
0,63 |
|
0,87 |
|
||

Повторение независимых испытаний
Формула Бернулли
Вероятность того, что в серии из независимых испытаниях, в каждом из которых вероятность появления события A равна p (0 р 1), это событие наступит ровно k раз (безразлично в какой последовательности), равна
где
C |
k |
|
n |
||
|
|
n! |
|
k! n k ! |
||
|
P |
k C k pk qn k |
n |
n |
|
– число сочетаний из n по k,
q=1-p
– вероятность противоположного события
A
.

В различных задачах нас могут интересовать следующие вероятности:
– вероятность того, что в испытаниях событие A наступит
менее m раз |
|
|
0 P 1 ... P |
m 1 ; |
||||||
P k m |
P |
|||||||||
n |
|
n |
|
|
n |
n |
|
|
|
|
– вероятность того, что в |
испытаниях событие A наступит |
|||||||||
более m раз |
|
|
|
|
|
|
|
|
|
|
P k m |
P |
m 1 P m 2 ... P n ; |
||||||||
n |
|
n |
|
|
n |
|
n |
|||
– вероятность того, что в |
испытаниях событие A наступит не |
|||||||||
менее m раз |
|
|
|
|
|
|
|
|
|
|
P k m |
P |
m P |
m 1 ... P n ; |
|||||||
n |
|
|
|
n |
n |
|
n |
|||
– вероятность того, что в испытаниях событие A наступит не |
||||||||||
более m раз |
k m |
P 0 P 1 ... P m ; |
||||||||
P |
||||||||||
n |
|
|
|
|
n |
n |
n |
|||
– вероятность того, что в испытаниях событие A наступит не |
||||||||||
менее 1 и не более 2 раз |
|
|
|
|
|
|||||
P |
k k k |
|
P k1 |
... P k2 |
|
|
|
|||
|
|
|
||||||||
n |
1 |
2 |
|
|
n |
|
n |
|
|
|

Приближенные формулы Лапласа 1. Локальная формула Лапласа (Муавра - Лапласа)
Если число испытаний n велико, а вероятность p не очень
мала, то
P |
k |
1 |
x , |
n |
|
npq |
|
|
|
|
|
x |
1 |
|
2 |
/ 2 |
|
где |
|
e |
x |
, |
||
2 |
|
|
||||
|
|
|
|
|
|
Значения функции
x k np . 
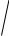 npq
npq
приведены в таблице.
При > 5 полагают |
≈ 0. |
|
|
Функция четная, и, |
следовательно, − |
= |
. |
2. Интегральная формула Лапласа
Вероятность того, что событие А появится в n испытаниях не менее 1 и не более 2 раз находится по формуле
где
|
|
P |
k |
k k |
2 |
x |
2 |
x |
, |
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
k |
|
np |
|
||
x |
1 |
|
x |
|
z |
/ 2 |
|
x |
x dz, |
|
|
|
k |
np |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
dz |
|
|
|
|
x |
|
|
2 |
|
. |
|||||||||
|
|
e |
|
x |
1 |
|
, |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
npq |
|
|
2 |
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значения функции Лапласа Ф приведены в таблице. При > 5 полагают Ф ≈ 0,5.
Функция Ф нечетная, и, следовательно, Ф − = −Ф .

Приближенная формула Пуассона
Если число испытаний n велико, а вероятность p появления события в каждом испытании очень мала, то
|
k (np) |
k |
e |
np |
P |
|
. |
||
n |
|
k! |
|
|
|
|
|
|
Обозначив =np – среднее число успехов в серии испытаний, получим
|
|
k |
e |
|
|
P |
k p(k; ) |
|
|
. |
|
|
|
|
|||
n |
|
|
k! |
|
|
|
|
|
|
||
Значение , по заданным k и можно определить по таблице.

Наивероятнейшее число успехов
Число k0 называется наивероятнейшим, если вероятность 0 того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей , k= 0, 1, … , n .
Наивероятнейшее число k0 определяется из двойного неравенства
np q k |
0 |
np p, |
|
|
причем:
а) если число − – нецелое, то существует единственное k0;
б) если число − – целое, то наивероятнейших числа два, а
именно: ′0 = − и ′′0 = + = ′0+1;
в) если – целое, то 0 = .
