1.3. Представление и кодирование информации

Естественные и формальные языки. Для обмена информацией используются естественные и формальные языки. Основное отличие формальных языков от естественных состоит в том, что формальные языки имеют строгие правила составления слов и предложений. Эти правила называются синтаксисом. Примером естественных языков являются русский язык, английский, китайский и т.д. Примерами формальных языков являются языки программирования, системы счисления, азбука Морзе.

В основе любого языка лежит набор определенных символов (знаков), который называется алфавитом. Алфавит любого естественного языка состоит из букв или иероглифов. Алфавит формального языка может состоять как из букв и иероглифов, так и из других символов, например, точки и тире (азбука Морзе), цифр (системы счисления), скрипичные ключи (ноты) и т.д.

Представление информации. Символы и знаки, составляющие алфавит языка, могут быть представлены в различных формах. Например, для представления информации с использованием языка в письменной форме используются знаки, которые являются изображениями на бумаге или других носителях, в устной речи в качестве знаков используются различные звуки, а при обработке текста на компьютере знаки представляются в форме двоичных кодов (последовательностей электрических импульсов).

Кроме изображений, звуков и электрических импульсов существуют и другие формы представления информации, например:

- световые сигналы (цветомузыка);

- радиоволны (радио);

- нервные импульсы (воздействие света, температуры на человека);

- магнитные записи (аудиокассеты, видеокассеты);

- жесты и мимика (язык глухонемых);

- запахи и вкусовые ощущения (информация о продукте питания);

- молекулы ДНК (генетическая информация) и т.д.

Кодирование информации. Часто при работе с информацией ее приходится переводить из одной формы представления в другую. Этот процесс называется кодированием.

Например, при вводе знака алфавита в компьютер путем нажатия соответствующей клавиши клавиатуры происходит кодирование информации, то есть преобразование знака в компьютерный код. При выводе знака на экран монитора происходит обратный процесс, когда компьютерный код знака преобразуется в его графическое изображение. Процесс восстановления данных в первичной форме называется декодированием.

Все виды информации в компьютере кодируются на машинном языке, в виде последовательностей нулей и единиц. Каждая цифра машинного двоичного кода несет информацию в 1 бит (так как всего есть два варианта – 0 и 1 – то при появлении одной из них неопределенность знаний уменьшается в два раза), по этому количество информации в битах равно количеству цифр двоичного машинного кода.

Вопросы:

1. Чем отличаются естественные языки от формальных?

2. Язык жестов глухонемых является формальных или естественных?

3. В какой форме информация представлена в сети Интернет?

4. Почему каждая цифра машинного двоичного кода несет информацию в 1 бит?

1.4. Системы счисления

Системы счисления. Практически в любой информации, с которой приходится сталкиваться человеку, содержатся числа. Для записи чисел используются особые формальные языки. Эти языки называются системами счисления, в них числа записываются по определенным правилам с помощью символов некоторого алфавита. Символы алфавита системы счисления называются цифрами. Например, в десятичной системе счисления, с которой обычно работает человек, числа записываются с помощью десяти цифр: 0, 1, 2, 3, 4 , 5, 6, 7, 8, 9. В двоичной системе счисления используется только две цифры: 0 и 1, а в шестнадцатеричной системе кроме цифр десятичной системы счисления используются буквы латинского алфавита: A, B, C, D, E (эти буквы соответствуют цифрам 11, 12, 13, 14, 15).

Все системы счисления делятся на позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных – не зависит.

Римская система счисления. Самой известной непозиционной системой счисления является римская. В качестве цифр в ней используются следующие буквы латинского алфавита: I (соответствует значению 1), V (5), X (10), L (50), C (100), D (500), M (1000). Так как римская система счисления непозиционная, то значение цифры не зависит от ее положения в числе. Например, в числе XX цифра X встречается два раза, и каждый раз обозначает одну и ту же величину – число 10. Тогда число XX будет равно 20 (10+10).

Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.

Задача 1.15. Перевести из римской системы счисления в десятичную:

а) XV; б) XIX;

в) MMDCCCLXXVII; г) MCDXLV.

Решение:

а) В данном числе всего две цифры, причем цифра, стоящая справа меньше. Это значит, что значением числа будет сумма этих цифр: XV=10+5=15.

б) Если количество цифр в числе больше 2, то начинаем перевод с первых двух чисел – XI. Так как меньшая цифра стоит правее, то первая цифра будет обозначать свое значение – 10. Первую цифру отбрасываем, и дальше будем рассматривать следующие две цифры – IX. Так как в этом случае меньшая цифра стоит левее, то значение этих двух цифр будет равно разности 10 – 1=9. Таким образом, получили, что число XIX=10+(10 – 1)=19.

в) Начинаем с первых двух цифр – MM. Так цифры одинаковые (главное, что цифра, стоящее правее не больше), то значение первой цифры будет равно 1000. Первую цифру отбрасываем и дальше рассматриваем следующие две цифры – MD. В этом случае снова цифра, стоящая правее, не больше цифры, стоящей левее. Значит, вторая цифра так же будет равна своему значению (1000). Рассматриваем следующие две цифры – DC. Продолжая процесс заметим, что все цифры числа расположены в неубывающем порядке. Значит, MMDCCCLXXVII=1000+1000+500+100+100+100+50+10+10+5+1+1=2877.

г) Начинаем с первых двух цифр – MC. Правая цифра меньше, значит, первая цифра равна 1000. Рассматриваем следующие две цифры – CD. Так как права цифра больше, то вместе эти две цифры будут равны 500–100 =400. Отбрасываем обе эти цифры, рассматриваем следующие – XL. Правая цифра больше, поэтому вместе эти цифры будет равны 50–10=40. Отбрасывает обе эти цифры. Осталась одна цифра, которая будет равна своему значению (5). Таким образом, получили, что MCDXLV=1000+400+40+5=1445.

Ответы: а) 15; б) 19; в) 2887; г) 1445. 

При переводе из десятичной системы счисления в римскую стоит учитывать, что разряды, начинающиеся с цифр 4 и 9, записывают в виде сочетания двух цифр римской системы: 4=IV, 9=IX, 40=XL, 90=XC, 400=CD, 900=CM.

Задача 1.16. Перевести из десятичной системы счисления в римскую:

а) 2589; б) 694; в) 1999.

Решение:

Перевод из десятичной системы счисления в римскую намного проще. В этом случае достаточно просто перевести все разряды слева направо в римскую систему счисления и полученные результаты соединить.

а) Разложим данное число на разряды: 2589=2000+500+80+9. Переведем каждый разряд в римскую систему счисления: 2000=1000+1000=ММ, 500=D, 80=50+10+10+10=LXXX, 9=IX. Тогда данное число будет равно: 2589=MMDLXXXIX.

б) Проделаем аналогичные действия: 694=600+90+4. 600=500+100=DC, 90=XC, 4=IV. Получим 694=DCXCIV.

в) 1999=1000+900+90+9. 1000=M, 900=CM, 90=XC, 9=IX. 1999=MCMXCIX.

Ответы: а) MMDLXXXIX; б) DCXCIV; в) MCMXCIX. 

Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит и основание. Основание позиционной системы счисления равно количеству цифр алфавита. То есть, в десятичной системе счисления основание равно 10, в двоичной – 2, в восьмеричной – 8 и т.п.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Например, в десятичной системе счисления первая цифра справа обозначается количество единиц, вторая – количество десятков, третья – количество сотен и т.д. Если в соседних позициях стоят одинаковые цифры, то значениях этих цифр отличаются в десять раз (в двоичной системе в два раза, в восьмеричной – в восемь).

В общем случае цифра а, стоящая в разряде n, равна аg^n-1, где g – основание системы счисления. Действительно, цифра 4, стоящая в третьем разряде числа, записанного в десятичной системе счисления равна 410^3-1 =400.Очевидно, что любое число, можно разложить в виде суммы значений цифр (например, 5678=5000+600+70+8). А каждое значение цифры можно записать в виде аg^n-1 (5000=510³, 600=610²,70=710¹, 8=810⁰).Это значит, что каждое число можно записать в так называемом развернутом виде (форме) (5678=510³+610²+710¹+810⁰). Дробное число 78,52 в развернутом виде запишется следующим образом 710¹+810⁰+510^-1+210^-2. Привычная для нас форма записи числе называется свернутая.

Стоит отметить важное свойство позиционных систем счисления: если число умножить (разделить) на основание системы счисления, то запятая, отделяющая целую часть от дробной, переместится на один разряд вправо (влево). Например, 25,6710=256,7.

Самой распространенной позиционной системой счисления является десятичная. Мы не будем подробно останавливаться на этой системе счисления, так как она достаточно подробно изучается в курсе математики средней школы. Из других позиционных систем счисления наиболее распространенными являются двоичная, восьмеричная и шестнадцатеричная.

Двоичная система счисления. Алфавит двоичной системы состоит из двух цифр (0 и 1), а значит основание равно 2. То что, число записано в двоичной системе счисления указывается нижним индексом 2 справа (11101₂). Если индекс у числа не стоит, то считается, что оно записано в десятичной системе. Любое число двоичной системы счисления можно записать в развернутой форме в виде суммы степеней числа 2 с коэффициентами, в качестве которых выступают цифры 0 и 1. Например, 1101₂=12³+12²+02¹+12⁰.

Умножение (деление) двоичного числа на 2 приведет к перемещению запятой на один разряд вправо (влево). Например, 101,01₂2=1010,1₂.

Позиционные системы счисления с произвольным основанием. Рассмотрим произвольную систему счисления с основанием g (g>1). В этой системе счисления алфавит состоит из g цифр: 0,1,…,g-2,g-1. Если g<11, то известных нам цифр хватит. А вот если g>10, то тогда для записи цифр, больших 9, используются буквы латинского алфавита. Цифра А равна 10, цифра В – 11, цифра С – 12 и т.д.

Если g=16 (шестнадцатеричная система счисления), то в качестве цифр будут использоваться буквы А, В, С, D, E и F. Число в шестнадцатеричной системе может выглядеть следующим образом: 6С4А₁₆. Это число в развернутом виде запишется так 616³+С16²+416¹+А16⁰ или 616³+1216²+416¹+1016⁰.

Перевод чисел в десятичную систему счисления. Для перевода числа из недесятичной системы счисления в десятичную достаточно записать число в развернутой форме и вычислить его значение.

Задача 1.17. Перевести числа в десятичную систему счисления:

а) 10101,01₂; б) 2547,7₈; в) A1D,E₁₆.

Решение:

Запишем данные числа в развернутой форме и вычислим их значения.

а) 10101,01₂=12⁴+02³+12²+02¹+12⁰+02^-1+12^-2=16+0+4+0+1+0+0,25= 21,25.

б) 2547,7=28³+58²+48¹+78⁰+78^-1=1024+320+32+7+0,875=1383,875.

в) A1D,E₁₆=A16²+116¹+D16⁰+E16^-1=1016²+116¹+1316⁰+1416^-1= 2560+16+13+0,875= 2589,875.

Ответы: а) 21,25; б) 1383,875; в) 2589,875. 

Перевод целых чисел из десятичной системы счисления. Перевод чисел из десятичной системы счисления в недесятичную более сложен и может осуществляться различными способами.

Рассмотрим сначала перевод целого десятичного числа а в систему счисления с основанием g. Отметим, что если a < g, то a₁₀ = a_g (например, 6₁₀=6₈, 1₁₀ = 1₂, 12₁₀=С₁₆). Будем считать, что a g.

1. Разделим а на g с остатком: a = ga₁ + r₁. Получим неполное частное а₁ и остаток r₁ (0r₁<g).

2. Если a₁<g, то процесс остановим, иначе разделим а₁ на g с остатком: a₁ = ga₂+r₂. Получим неполное частное а₂ и остаток r₂ (0r₂<g).

3. Если а₂<g, то процесс остановим, иначе разделим а₂ на g с остатком и будем продолжать процесс пока не получим неполное частное меньшее основания g.

Пусть в результате перевода мы n раз выполняли процесс деления и получили остатки r₁, r₂, r₃, …, r_n-1, r_n и последнее неполное частное a_n (0<a_n<g). Тогда число а₁₀ в системе счисления с основанием g запишется в виде последовательности цифр a_n, r_n, r_n-1,…, r₃, r₂, r₁.

Задача 1.18. Перевести число 159 в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Решение:

Выполним перевод в двоичную систему счисления:

1. Разделим 159 на 2 остатком: 159=279+1. Получили неполное частное 79 и остаток 1. так 79 ≥ 2, то продолжим процесс. Последней цифрой в двоичной записи числа 159 будет 1 (r₁=1).

2. Раздели 79 на 2 с остатком: 79=239+1. Так как 39 ≥ 2, то продолжаем процесс. Второй с конца цифрой будет 1 (r₂=1).

3. Разделим 39 на 2 с остатком: 39=219+1 (r₃=1).

4. Разделим 19 на 2 с остатком: 19=29+1 (r₄=1).

5. Разделим 9 на 2 с остатком: 9=24+1 (r₅=1).

6. Разделим 4 на 2 с остатком: 4=22+0 (r₆=0). Так как 2 ≥ 2, то продолжаем процесс.

7. Разделим 2 на 2 с остатком: 2=21+0. (r₇=0). Получили, что а₇=1 < 2, а значит процесс останавливаем и получаем, что 159=10011111₂.

Выполним перевод в восьмеричную систему счисления:

1. Разделим 159 на 8 с остатком: 159=819+7 (r₁=7).

2. Разделим 19 на 8 с остатком: 19=82+3 (r₂=3). а₂=2 < 8, процесс останавливаем и получаем, что 159=237₈.

Выполним перевод в шестнадцатеричную систему счисления:

1. Разделим 159 на 16 с остатком: 159=169+15 (r₁=15=F₁₆). а₁=9 < 16, процесс останавливаем и получаем, что 159=9F₁₆.

Ответы: 159=10011111₂=237₈=9F₁₆. 

Перевод дробных чисел из десятичной системы счисления. Рассмотрим алгоритм перевода дробного десятичного числа а в систему счисления с основанием g (Отметим, что число а имеет целую часть равную 0):

1. Умножим число а на основание g: ag=b₁+a₁. Получили число с целой часть b₁ и дробной частью а₁. Если а₁=0, то процесс останавливаем, иначе продолжаем.

2. Умножим число а₁ на g: a₁g=b₂+a₂. Если а₂=0 то процесс останавливаем, иначе продолжаем процесс до тех пор, пока не получим дробную часть равную нулю. Отметим, что этот процесс может быть бесконечным. В этом случае мы получим бесконечную дробь.

Пусть в результате n действия мы получили целые части b₁, b₂,…, b_n-1, b_n. Тогда число а в системе счисления с основанием g запишется в виде числа с целой часть, равной 0, и дробной частью, которая запишется в виде последовательности цифр b₁, b₂,…, b_n-1, b_n.

Задача 1.19. Перевести число 0,9375 в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Решение:

Выполним перевод в двоичную систему счисления:

1. Умножим 0,9375 на 2: 0,93752=1,875=1+0,875 (b₁=1). Получили целую часть равную 1 и дробную часть равную 0,875. Так как дробная часть отлична от нуля, то продолжаем процесс.

2. Умножим 0,875 на 2: 0,8752=1,75=1+0,75 (b₂=1).

3. 0,752=1,5=1+0,5 (b₃=1).

4. 0,52=1+0 (b₄=1). Так как дробная часть равна 0, то процесс останавливаем и получаем 0,9375=0,1111₂.

Выполним перевод в восьмеричную систему счисления:

1. Умножим 0,9375 на 8: 0,93758=7,5=7+0,5 (b₁=7).

2. 0,58=4+0 (b₂=4). Так как дробная часть равна 0, то процесс останавливаем и получаем 0,9375=0,74₈.

Выполним перевод в шестнадцатеричную систему счисления:

1. Умножим 0,9375 на 16: 0,937516=15+0 (b₁=15=F₁₅). Так дробная часть равна 0, то процесс останавливаем и получаем 0,9375=0,F₁₆.

Ответы: 0,9375=0,1111₂=0,74₈=0,F₁₆. 

Отметим, что перевод чисел, содержащих и целую и дробную части производится в два этапа. Отдельно переводятся целая и дробная части. В итоговой записи полученного числа целая часть от дробной отделяется запятой.

Арифметические операции в двоичной системе счисления. Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам. Рассмотрим сначала действия с двоичными числами. Для удобства вычислений рассмотрим сначала таблицы сложения, вычитания и умножения двоичных чисел.

+	0	1		-	0	1			0	1
0	0	1		0	0	*		0	0	0
1	1	10		1	1	0		1	0	1

Таблицы 1.2.-1.4. Таблицы сложения, вычитания, умножения двоичных чисел.

* - о записи отрицательных чисел см. в п. 1.5.

Действия с двоичными числами выполняются аналогично действиям с десятичными числами. Рассмотри пример:

Задача 1.20. Пусть а=1001₂, b=11₂. Найти а+b, а-b, аb и а/b. Сделать проверку.

Решение:

Выполним все необходимые действия в столбик:

Таким образом, получили, что 1001₂+11₂=1100₂=с₁, 1001₂–11₂=110₂=с₂, 1001₂11₂=11011₂=с₃, 1001₂/11₂=11₂=с₄.

Для проверки переведем числа а, b и все получившиеся результаты в десятичную систему счисления:

а=1001₂=12³+02²+02¹+12⁰=8+0+0+1=9;

b=11₂=12¹+12⁰=2+1=3;

с₁=1100₂=12³+12²+02¹+02⁰=8+4+0+0=12;

с₂=110₂=12²+12¹+02⁰=4+2+0=6;

с₃=11011₂=12⁴+12³+02²+12¹+12⁰=16+8+2+1=27;

с₄=11₂=3.

Проверим получившиеся результаты:

а+b=с₁ 9+3=12 – верно; а–b=с₂ 9–3 =6 – верно;

аb=с₃ 93=27 – верно; а/b=с₄ 9/3=3 – верно.

Ответы: а+b=1100₂; а–b=110₂; аb=110011₂; а/b=11₂. 

Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Аналогично выполняются действия и в других позиционных системах счисления. Рассмотрим таблицы сложения и умножения для восьмеричной и шестнадцатеричной систем счисления.

+	0	1	2	3	4	5	6	7		*	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7		0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	10		1	0	1	2	3	4	5	6	7
2	2	3	4	5	6	7	10	11		2	0	2	4	6	10	12	14	16
3	3	4	5	6	7	10	11	12		3	0	3	6	11	14	17	22	25
4	4	5	6	7	10	11	12	13		4	0	4	10	14	20	24	30	34
5	5	6	7	10	11	12	13	14		5	0	5	12	17	24	31	36	43
6	6	7	10	11	12	13	14	15		6	0	6	14	22	30	36	44	52
7	7	10	11	12	13	14	15	16		7	0	7	16	25	34	43	52	61

Таблицы 1.5 и 1.6. Таблицы сложения и умножения восьмеричных чисел.

+	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11
3	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12
4	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13
5	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14
6	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15
7	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16
8	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17
9	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18
A	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19
B	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A
C	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B
D	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C
E	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D
F	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D	1E

Таблица 1.7. Таблица сложения шестнадцатеричных чисел.

*	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	0	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	0	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	0	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	0	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	0	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	0	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	0	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	0	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	0	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C	0	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	0	D	1A	27	34	41	4E	5B	68	75	92	8F	9C	A9	B6	C3
E	0	E	1C	2A	35	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	0	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Таблица 1.8. Таблица умножения шестнадцатеричных чисел.

Задача 1.21. Пусть а=50₈, b=12₈. Найти а+b, а-b, аb и а/b. Сделать проверку.

Решение:

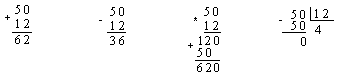
Таким образом, получили, что 50₈+12₈=62₈=с₁, 50₈–12₈=36₈=с₂, 50₈12₈=620₈=с₃, 50₈/12₈=4₈=с₄.

Для проверки переведем числа а, b и все получившиеся результаты в десятичную систему счисления:

а=50₈=58¹+08⁰=40+0=40;

b=12₈=18¹+28⁰=8+2=10;

с₁=62₈=68¹+28⁰=48+2=50;

с₂=36₈=38¹+68⁰=24+6=30;

с₃=620₈=68²+28¹+08⁰=384+16+0=400;

с₄=4₈=4.

Проверим получившиеся результаты:

а+b=с₁ 40+10=50 – верно; а–b=с₂ 40–10 =30 – верно;

аb=с₃ 4010=400 – верно; а/b=с₄ 40/10=4 – верно.

Ответы: а+b=62₈; а–b=36₈; аb=620₈; а/b=4₈. 

Задача 1.22. Пусть а=1А9₁₆, b=37₁₆. Найти а+b, а-b, аb и а/b. Сделать проверку.

Решение:

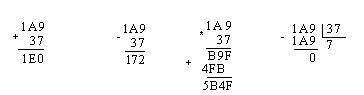
Таким образом, получили, что 1А9₁₆+37₁₆=1E0₁₆=с₁, 1А9₁₆–37₁₆=172₈=с₂, 1А9₁₆37₁₆=5B4F₁₆=с₃, 1А9₁₆/37₁₆=7₁₆=с₄.

Для проверки переведем числа а, b и все получившиеся результаты в десятичную систему счисления:

а=1А9₁₆=116²+1016¹+916⁰=256+160+9=425;

b=37₁₆=316¹+716⁰=48+7=55;

с₁=1E0₁₆=116²+1416¹+016⁰=256+224+0=480;

с₂=172₁₆=116²+716¹+216⁰=256+112+2=370;

с₃=5B4F₁₆=516³+1116²+416¹+1516⁰=20480+2816+64+15=23375;

с₄=7₁₆=7.

Проверим получившиеся результаты:

а+b=с₁ 425+55=480 – верно; а–b=с₂ 425–55 =370 – верно;

аb=с₃ 42555=23375 – верно; а/b=с₄ 425/55=7 – верно.

Ответы: а+b=1E0₁₆; а–b=172₁₆; аb=5B4F₁₆; а/b=7₁₆. 

Вопросы:

1. Знаете ли Вы какие-нибудь непозиционные системы счисления кроме римской?

2. Что случится с запятой, разделяющей целую и дробные части числа, если число умножить (разделить) на квадрат основания системы счисления, в которой записано число?

3. Какой алфавит у системы счисления с основанием 20?

4. Может ли быть процесс перевода целых чисел из десятичной системы счисления в недесятичную бесконечным?

5. Запишите таблицу сложения и умножения для троичной системы счисления.

Задачи для самостоятельного решения:

Задача 1.23. Перевести из римской системы счисления в десятичную:

а) XIV; б) CDIX;

г) MDCXCIV; д) MMDCCXCIX.

Задача 1.24. Перевести из десятичной системы счисления в римскую:

а) 1444; б) 2999; в) 3456.

Задача 1.25. Запишите числа в развернутой форме:

а) 10257; б) 10011,001₂; в) 5467,25₈; г) ААС,01₁₆.

Задача 1.26. Перевести числа в десятичную систему счисления:

а) 1010₂; б) 1100,01₂; в) 234₇;

г) 756,4₇; д) А0₁₆; е) F1,С₁₆.

Задача 1.27. Перевести числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную:

а) 1000; б) 0,125; в) 164,75.

Задача 1.28. Найти а+b, а-b, аb и а/b и сделать проверку, если:

а) а=1100₂, b=110₂; б) а=110₈, b=11₈; в) а=24₁₆, b=С₁₆.