Раздел_1
.doc
-
УРАВНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА С УЧЕТОМ ЕГО УПРУГИХ, ТЕПЛОВЫХ И ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ
В
общем случае тепловые, электромагнитные
и упругие процессы в твёрдом теле
взаимосвязаны и взаимообусловлены. Об
этом убедительно свидетельствует хотя
бы приведённый выше краткий обзор
пъезоактивных свойств твёрдых тел. На
рис. 1.1.1 схематически представлены
связи между характеристиками физических
полей в реально существующем деформируемом
твёрдом теле. При этом напряжённо-деформированное
состояние (упругие поля) характеризуется
набором компонентов тензора напряжения
и деформации
;
магнитное поле описывается с помощью
компонентов вектора напряжённости
и магнитной индукции
;
электрическое поле представлено
компонентами векторов напряжённости
и индукции
,
и, наконец, тепловое поле задано с помощью
значений температуры
и энтропии
.
Множество двунаправленных стрелок на
рис. 1.1.1 подчёркивают то обстоятельство,
что все вышеперечисленные величины
взаимосвязаны.
Значения
и характер изменения представленных
на рис. 1.1.1 величин практически
полностью определяет состояние твёрдого
тела. В рамках симметричной теории
упругости (в отличие от теории братьев
Коссера [1]) тензоры
и
имеют всего лишь по шесть, в общем случае,
неравных между собой компонентов и
поэтому можно утверждать, что состояние
твёрдого тела описывается с помощью 26
переменных. Для того чтобы построить
функциональные соотношения между этими
переменными, разделим их на две группы.
Одну группу переменных (обозначим её
символом
)
будем называть независимыми переменными,
вторую, равную первой по числу элементов,
группу обозначим символом
,
а входящие в нее физические величины
будем называть зависимыми переменными.
Разбитие входящих в схему (рис. 1.1.1)
величин на зависимые и независимые
переменные осуществляется с известной
долей произвола, по усмотрению расчётчика.
Примерные варианты разбиения показаны
в таблице
|
|
|
|
|
|
… |
|
|
|
|
|
|
… |
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Особых
оснований для того, чтобы отдать
предпочтение какому либо конкретному
набору величин
и
не существует, и поэтому выберем в
качестве независимых переменных набор
из тринадцати величин
,
,
и
.
Оставшиеся 13 величин будут являться
зависимыми переменными, т. е. функциями
независимых переменных:
,
,
и
.
Предположим,
что при некоторой температуре
в твёрдом теле отсутствуют деформации,
электрические и магнитные поля, т. е.
=0,
=0,
=0.
При таком наборе независимых переменных
будем полагать, что
,
,
и
.
Определённый выше набор независимых и
зависимых переменных описывает некоторое
начальное состояние твёрдого тела,
которое будем в дальнейшем называть
естественным.
Предположим,
что с помощью каких-либо устройств в
твёрдом теле, пребывающем в естественном
состоянии, возбуждаются электрические,
магнитные и тепловые поля, т.е. появляются
отличнее от нуля компоненты
,
,
и
.
При этом будем считать, что возмущения
независимых переменных невелики.
Последнее предположение позволяет
разложить функции
,
...,
в ряды Тейлора, ограничившись при этом
лишь линейными членами разложения.
Принимая во внимание определение
естественного состояния, можно записать,
что
,
,
,
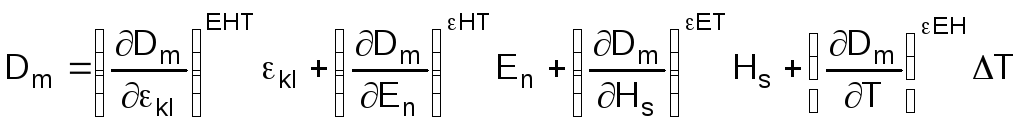(1.1.1)
,
где
запись
обозначает константу, определённую при
фиксированных значениях (в режиме
постоянства) величин
,
и
;
соответственно, аналогичный смысл имеют
другие подобного рода записи;
;
.
Следует обратить внимание на то, что система уравнений (1.1.1) записана в предположении о линейной связи между напряженно-деформированным состоянии и электромагнитным полем, т.е. уравнения (1.1.1) описывают состояния линейного пьезоактивного твёрдого тела.
В уравнения (1.1.1) входят 16 констант. Вполне вероятно, что некоторые из этих 16 констант как-то связанны между собой. Для выявления связей между константами в системе уравнений (1.1.1) обратимся к методам термодинамики – науки, которая по образному выражению всемирно известного физика Ричарда Филипса Фейнмана занимается «поисками соотношений между различными свойствами вещества, не углубляясь в изучение его внутреннего строения».
Прежде
всего, запишем первый закон термодинамики,
согласно которому приращение запасаемой
в твёрдом теле энергией
(приращение внутренней энергии)
складывается из притока тепла
и приращения работы внешних сил
,
т.е.
.
(1.1.2)
В
любом из курсов термодинамики (см.,
например, [2, 3]) доказывается, что
.
Что касается приращения работы внешних
сил, то эту величину можно представить
как сумму трех составляющих. Первая
составляющая ‑
– представляет работу внешних сил,
которая производится над единичным
объемом твердого тела при изменении
деформации на малую величину
.
Второе слагаемое −
− полная работа электрических сил,
связанная с изменением поляризации
материала в единичном объеме деформируемого
твердого тела. Третья составляющая −
−
работа сил магнитного поля.
Таким образом, соотношение (1.1.2) приобретает следующий вид:
.
(1.1.3)
Необходимо заметить, что левые и правые части уравнений (1.1.2) и (1.1.3) имеют размерность [джоуль/куб. м], т. е. речь идет об объемной плотности энергии.
Теперь рассмотрим термодинамический потенциал Гиббса [3]
,
с помощью которого становиться возможным связать воедино зависимые и независимые переменные. Для каждого конкретного набора независимых переменных существует свой термодинамический потенциал, методика их построения в доступной форме изложена в работе [3]; в монографии [4] приводится ряд конкретных термодинамических потенциалов.
Определим дифференциал потенциала Гиббса (Джозайя Уиллард Гиббс, 11.02.1839–28.04.1903):
.
(1.1.4)
Подставляя в выражение (1.1.4) дифференциал внутренней энергии (1.1.3), получаем:
,
(1.1.5)
откуда
отчетливо видно, что потенциал Гиббса
является функцией независимых переменных
,
,
и
,
и его дифференциал может быть записан
в виде:
.
(1.1.6)
Сопоставляя выражения (1.1.5) и (1.1.6), приходим к выводу, что
.
(1.1.7)
Определенные
соотношениями (1.1.7) величины
,
,
и
,
подставим в производные в разложениях
(1.1.1):
,
,
,
.
(1.1.8)
Если
правые части системы уравнений (1.1.8)
представить в виде квадратной таблицы
и провести в этой таблице диагональ из
левого верхнего угла в правый нижний,
то легко заметить, что на самой диагонали
расположились величины, в которые в
качестве сомножителей входят константы,
определяемые при трех фиксированных
переменных. Вне главной диагонали
константы определяются только лишь при
двух фиксированных переменных. Но,
пожалуй, самое главное свойство этой
таблицы заключается в том, что константы,
расположенные симметрично относительно
проведенной диагонали, имеют один и тот
же физический смысл, т. е. являются
различными компонентами одной и гой же
физической величины. Действительно,
если обозначить:
,
то
.
Отмеченное соответствие между симметрично расположенными относительно диагонали таблицы константами, позволяет утверждать, что физические свойства пьезоактивного твердого тела в общем виде описываются с помощью десяти наборов материальных констант. Введем обозначения:
– модуль
упругости, экспериментально определяемый
в режиме постоянства температуры и
напряженностей электрического и
магнитного полей;
– пьезоэлектрический
модуль, экспериментально определяемый
в режиме постоянства температуры и
напряженности магнитного поля;
– компонент
тензора диэлектрической проницаемости,
экспериментально определяемый в режиме
постоянства температуры деформации и
напряженности магнитного поля;
– пьезомагнитный
модуль;
– магнитоэлектрическая
постоянная;
–
компонент
тензора магнитной проницаемости;
– компонент
тензора температурных напряжений;
– пироэлектрическая
константа;
– пиромагнитная
константа.
Что
же касается величины
,
то в любом курсе термодинамики
доказывается, что она в точности равна
отношению
,
где
– удельная теплоемкость, взятому с
противоположным знаком.
Необходимо
подчеркнуть, что постоянство температуры
характеризует изотермические процессы,
и поэтому все определенные выше
материальные константы могут содержать
дополнительное прилагательное
«изотермический», например: изотермический
модуль упругости
,
изотермический пьезоэлектрический
модуль
и т. д.
С учетом введенных обозначений систему уравнений (1.1.8) можно записать в следующем виде:
;
;
;
.
(1.1.9)
Как правило, пьезоэлектрические и пьезомагнитные свойства одновременно не проявляются, т. е. твердое тело является либо пьезоэлектриком либо пьезомагнетиком.
Полагая в уравнениях состояния (1.1.9) равными нулю все компоненты тензоров пьезомагнитных, магнитоэлектрических и пиромагнитных констант, получаем изотермические уравнения состояния пьезоэлектрика:
;
;
,
(1.1.10)
которые
дополняются уравнением магнитной
поляризуемости среды
.
В уравнениях физического состояния
(1.1.10) отсутствует верхний индекс
при символах материальных констант.
Тем самым подчеркивается, что магнитное
поле не оказывает какого-либо заметного
влияния на состояние твердого тела.
Рассуждая аналогичным образом, можно выделить из уравнений состояния (1.1.9) изотермические уравнения состояния пьезомагнитной среды:
;
;
,
(1.1.11)
которые
дополняются уравнением электрической
поляризуемости среды
.
Уравнения физического состояния (1.1.10) и (1.1.11) описывают медленно развивающиеся во времени процессы, при которых изменение напряженно-деформированного состояния и поляризации твердого тела сопровождается перераспределением тепла между отдельными объемами твердого тела. В ультразвуковой технике наблюдается диаметрально противоположная ситуация – напряженно-деформированное состояние и поляризация твердого тела меняют свой знак десятки, сотни тысяч раз в секунду, в устройствах акустоэлектроники частота изменения состояния пьезоактивного твердого тела порядка 106÷108 Гц. Очевидно, что в этом случае за время, равное периоду повторения знака состояния, различные объемы деформируемого пьезоактивного твердого тела не успевают обменяться теплом, и, стало быть, в каждой локальной области вещества происходит изменение состояния без изменения энтропии, – т. е. реализуется так называемый адиабатический процесс.
Уравнения
состояния, описывающие адиабатические
процессы в деформируемых и поляризуемых
твердых телах, конструируются следующим
образом: из условия адиабатичности
процесса, т. е. из условия
,
находится локальный перегрев
,
который впоследствии исключается их
двух других уравнений состояния. Так,
в случае пьезоэлектриков, из условия
находим, что:
.
(1.1.12)
Подставляя выражение (1.1.12) в правые части первых двух уравнений состояния (1.1.10), получаем адиабатический вариант уравнений состояния пьезоэлектриков:
(1.1.13)
где
,
и
– адиабатические модуль упругости,
пьезомодуль и диэлектрическая
проницаемость. Связь адиабатических
материальных констант с изотермическими
очевидна:
;
;
Аналогичным образом записывается пригодный для расчетов быстротекущих процессов адиабатический вариант уравнений состояния пьезомагнетиков:
(1.1.14)
где
;
;
.
Следует
заметить, что адиабатические и
изотермические материальные константы
твердых тел имеют, как правило, мало
отличающиеся числовые значения. Так,
для кварца при 25˚C
адиабатический модуль упругости
больше на 4,5% соответствующего
изотермического модуля, а значение
модуля
отличаются друг от друга на 0,189% [5].
Если
в уравнениях состояния (1.1.9) положить
равным нулю компоненты тензоров
,
,
,
,
т. е. разорвать связь между электромагнитными
и термоэлектрическими явлениями, то
получим изотермические уравнения
состояния обычного (не пьезоактивного)
твердого тела:
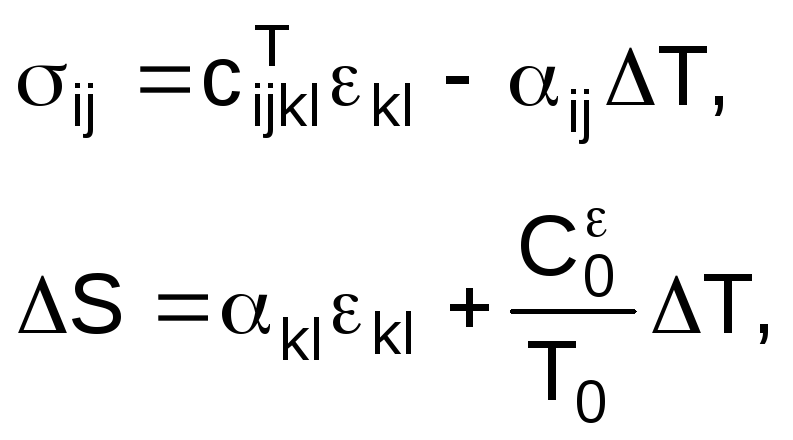(1.1.15)
которые дополняются уравнениями электрической и магнитной поляризации среды:
Уравнения физического состояния (1.1.15) описывают медленно изменяющиеся во времени термоупругие процессы в деформируемом твердом теле и называются уравнениями Дюамеля-Неймана [1]. Адиабатический вариант уравнений состояния непьезоактивного твердого тела имеет совсем простой вид:
,
(1.1.16)
где
.
Соотношение
(1.1.16) имеет структуру хорошо известного
закона Гука (
)
и по этой причине называется обобщенным
законом Гука.
Обратимся к уравнениям состояния сред со стрикционными эффектами.
Для
того, чтобы построить уравнения
физического состояния сегнетоэлектрического
материала необходимо выполнить все те
же действия, что и при выводе уравнений
состояния пьезоэлектриков. Отличия
заключаются в том, что при разложении
в ряд Тейлора функции
необходимо удерживать члены с четными
порядками производных по независимой
переменной
.
Производные нечетных порядков должны
быть приняты равными нулю в силу четности
электрострикционного (сегнетоэлектрического)
эффекта. В разложении функции
необходимо сохранить слагаемые, которые
содержат смешанные производные по
независимым переменным
и
.
Выполнение этих процедур не сопряжено
с какими-либо трудностями принципиального
порядка, но сопровождается весьма
громоздкими выкладками.
Чтобы избежать выполнения этой рутинной работы, воспользуется аналогией, которая, как было показано выше, существует между магнитострикционными и электрострикционными (сегнетоэлектрическими) эффектами.
В
1957 г. К. Б. Власов опубликовал статью
[6], в которой в наиболее общей и законченной
форме были выписаны изотермические
уравнения состояния магнитострикционных
сред. Эти уравнения, как и рассмотренные
выше уравнения состояния пьезоактивных
сред, получаются в результате разложения
в ряд Тейлора зависимых переменных с
удержанием соответствующих членов
разложения. Так, результирующее
механическое напряжение
по К. Б. Власову должно быть
представлено разложением следующего
вида:
.
Аналогичное по структуре выражение записывается для магнитной индукции.
В
подавляющем большинстве практически
интересных случаев нет необходимости
работать со столь громоздкими уравнениями
состояния магнитострикционной среды,
достаточно лишь сохранить в разложениях
,
то составляющие, которые соответствуют
качественному содержанию процессов
деформирования и магнитной поляризации
ферромагнетика. Исходя из этих соображений,
были построены усеченные (по сравнению
с предложенными К. Б. Власовым) уравнения,
которые справедливы в области небольших
значений деформаций, и в магнитных
полях, напряженность которых существенно
меньше напряженности поля насыщения
ферромагнетика. Адиабатический вариант
этих уравнений состояния имеет вид