
10
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
__________________________________________________________
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра физики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ
для студентов специальностей 060811, 060815, 240400, 290300, 290600, 290700, 290800, 291000, 2911000, 550100.
Лабораторная работа № 10
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ МЕТОДОМ КРУТИЛЬНОГО МАЯТНИКА
Казань
2005
Составители: |
В.И.Сундуков, |
|
И.А.Заводов |
Под редакцией |
В.В. Алексеева |
УДК 539.15 |
|
Методические указания к лабораторным работам по физике для сту- дентов дневного и заочного отделений специальностей 060811, 060815, 240400, 290300, 290600, 290700, 290800, 291000, 2911000, 550100 / Казан-
ский государственный архитектурно-строительный университет; Состави- тели В.И.Сундуков, И.А.Заводов. Под редакцией В.В. Алексеева. - Казань, 2005 г. 14 с.
В работе рассмотрены вопросы, связанные с кинематикой и динами- кой поступательного и вращательного движения. Описан принцип работы баллистического маятника.
Илл. 8
Рецензент доцент кафедры молекулярной физики |
|
Казанского госуниверситета |
Пименов |
Г. Г.
ã Казанский государственный архитектурно-строительный университет, 2005 г.
2

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ МЕТОДОМ КРУТИЛЬНОГО МАЯТНИКА.
(БАЛЛИСТИЧЕСКИЙ МАЯТНИК)
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Угловая скорость. Угловое ускорение. Пусть материальная точка вращается вокруг неподвижной оси. Для характеристики быстроты ее вра- щения вводится угловая скорость. Если за элементарный промежуток вре- мени dt радиус-вектор, соединяющий ее с центром окружности, повернулся на элементарный угол dϕ, то
υ |
|
ε |
|
|
угловая скорость ω равна: |
||||||
|
ω |
|
|
ω = dϕ , |
|
|
|
|
|||
|
|
|
|
|
r |
|
|
|
|
||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
||
|
|
|
|
ϕ |
т.е. угловая скорость равна |
||||||
|
|
|
|
||||||||
|
|
|
|
|
углу поворота, отнесенного к |
||||||
|
|
|
|
|
единице |
времени, или произ- |
|||||
|
|
|
|
|
водной |
угла |
поворота по |
||||
|
|
|
|
|
|||||||
|
|
|
|
|
времени. |
Направление |
этого |
||||
|
|
|
|
|
вектора |
определяется |
прави- |
||||
|
|
|
|
|
лом правого винта: при пово- |
||||||
|
|
|
|
|
|||||||
|
Рис. 1 |
|
|
роте винта |
в |
направлении |
|||||
|
|
|
вращения его |
поступатель- |
|||||||
|
|
|
|
|
ное движение дает направ- |
||||||
|
|
|
|
|
ление вектора ω |
(рис 1). |
|||||
3
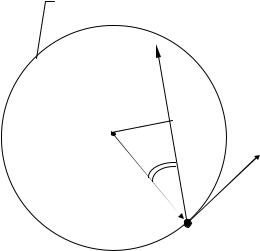
Вектор линейной скорости υ направлен по касательной к траектории (окружности) и ее модуль υ равен
υ = ω R,
где R - радиус окружности .
Угловая скорость может изменяться со временем. Быстроту ее измене- ния характеризуют угловым ускорением. Пусть за элементарный промежу- ток времени dt угловая скорость изменилась на величину dω . Тогда угло-
вое ускорение ε равно
ε = dω |
, |
|
r |
|
|
|
dt |
|
т.е. угловое ускорение это — изменение угловой скорости, отнесенное к единице времени. Направление углового ускорения при движении по ок-
ружности совпадает с направлением угловой скорости при ускоренном движении и противоположное − при замедленном.
В системе единиц СИ единицей угловой скорости является 1 рад/с, а углового ускорения — 1 рад/с2.
2. Момент силы относительно оси и точки. Пусть материальная точ-
ка массой m движется в инерциальной системе отсчета по окружности ра- диусом R под действием внешней силы F ( рис. 2 ). Моментом M силы относительно точки O называется векторное произведение радиуса- вектора, проведенного из этой точки до точки приложения силы, на эту силу.
|
|
|
|
M |
= [RF]. |
|
Траектория |
|
|
Момент |
силы |
относи- |
|
|
|
тельно оси |
обуславливает |
|||
|
|
|
|
|||
|
|
|
|
угловое ускорение тела и, |
||
|
|
|
|
следовательно, характери- |
||
|
|
|
|
зует вращательную способ- |
||
l |
|
F |
|
ность силы. |
|
|
О |
α |
|
ВекторM перпендику- |
|||
|
|
лярен к плоскости, прове- |
||||
|
|
|
||||
R |
|
|
υ |
денной через векторы R и |
||
|
|
F . Его направление нахо- |
||||
|
|
|
|
|||
|
|
|
|
дится по правилу правого |
||
|
|
|
|
винта: при вращении винта |
||
|
|
|
|
в направлении силы, его по- |
||
Рис. 2 |
|
|
|
ступательное движение да- |
||
|
|
|
ет направление |
момента |
||
|
|
|
|
|||
4
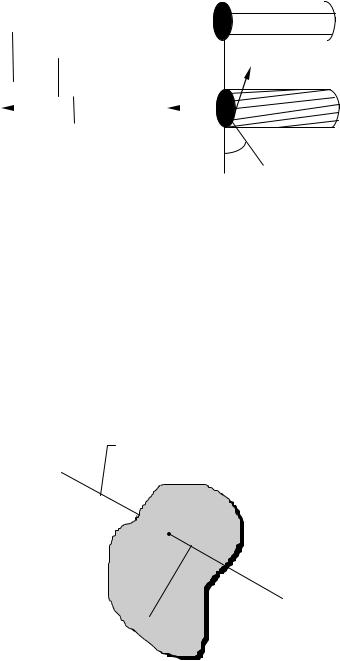
силы. На рис. 2 это − вектор выходящий перпендикулярно из плоскости чертежа. Модуль момента силы можно записать в ином виде, если учесть, что R· sinα = l является длиной перпендикуляра, опущенного из точки O на направление силы (рис. 2). Это расстояние называют плечом силы. Тогда
M = F l,
т.е. модуль момента силы равен произведению модуля силы на плечо.
3. Момент упругих сил. Известно, что при упругом растяжении или сжатии возникает сила Fупр= - k×x, направленная в сторону противополож-
\ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ную смещению (k − жесткость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пружины, x − величина дефор- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мации) (рис 3). Аналогичное |
|
|
x |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
Fупр |
|
|
|
соотношение можно записать и |
||||||||
|
|
|
|
|
|
|
|
Mупр |
|
|
|
для упругих деформаций типа |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кручения. Только вместо силы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
будет |
фигурировать момент |
|
Fупр |
|
|
|
|
|||||||||||
|
|
|
|
ϕ |
|
|
|
сил M, а вместо смещения − |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол закручивания ϕ (рис 3): |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис 3. |
|
|
|
|
М упр = -D ×ϕ , |
|||
|
|
|
|
|
|
|
|
|
|
|
D − |
некоторая постоянная по |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
смыслу аналогичная k.
4. Момент инерции твердого тела. Из опытов следует, что вращаю-
щиеся тела обладают способностью противодействовать изменению угло- вой скорости, которой они обладают. Это свойство тел было названо инертностью тела при вращательном движении. Инертность тела при вра- щении характеризуется инерции тела I.
Величина момента инерции материальной точки относительно оси вращения равна:
Ось вращения
Ri 
 mi
mi
Рис 4.
Ii = miR2i,
где m − масса, Ri − расстояние от оси вращения до точки.
Для нахождения момента инерции тела рассмотрим его как механическую систему матери- альных точек. Мысленно разо-
бьем тело на элементарные части массой mi , которые можно при- нять за материальные точки. Оче- видно, что момент инерции I тела
5
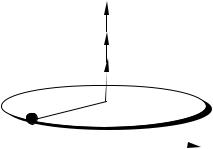
относительно оси равен сумме Ii отдельных элементарных частей тела от- носительно той же оси. При вращении тела все его точки движутся по ок- ружностям различного радиуса Ri , плоскости которых перпендикулярны к оси вращения (рис 4):
I.= å Ii = åmi Ri 2 .
ii
5.Момент импульса материальной точки, твердого тела. Закон со-
хранения момента импульса. По аналогии с моментом силы относитель-
но точки вводится понятие момента импульса. Моментом L импульса то-
чечного тела относительно точки называется векторное произведение радиуса-вектора R , проведенного из этой точки до точечного тела, на импульс mυ этого тела:
L = m×[Rυ].
Вектор L , как и момент силы перпендикулярен к плоскости, проведен- ной через векторы R и υ . Его направление находится по правилу право-
го винта (рис 5).
При движении материальной точки по окружности модуль момента импульса относительно центра окружности равен
|
|
L = m υ R, |
|
|
где R ¾ радиус окружности, m и u ¾ |
M |
|
масса и скорость данного тела. |
|
Если тело вращается вокруг некото- |
|
L |
|
рой оси с угловой скоростью ω , то мо- |
|
мент импульса твердого тела относи- |
|
ω |
|
|
|
тельно оси вращения равен произведе- |
|
R |
|
нию момента инерции тела относитель- |
|
но той же оси на его угловую скорость. |
|
|
|
|
|
|
r |
|
υ |
L = Iω. |
|
|
|
Рис 5 |
|
Из этой формулы следует, что направ- |
|
ления L и ω совпадают, т.к. произведе- |
|
|
|
|
|
|
ние вектора на положительный скаляр |
дает вектор того же направления (рис 5). |
||
Момент импульса |
L системы равен векторной сумме моментов им- |
|
пульсов тел входящих в эту систему: L = å Li . Момент импульса L замк-
i
6

нутой механической системы относительно оси или точки постоянен во времени.
L = const .
Это означает, что моменты импульсов отдельных тел системы могут изменяться, однако их векторная сумма остается неизменной. Данное ут- верждение − суть закона сохранения момента импульса.
6. Кинетическая энергия. Кинетической называется энергия, кото- рой обладает тело при своем движении.
Для поступательно движущегося тела эта энергия равна:
Wk поступ = 21 mυ 2 .
Кинетической энергией вращательного движения, называется энергия, которой обладает тело при вращении. Ее формулу легко получить если учесть, что для вращательного движения аналог массы m - момент инер- ции I, скорости - w:
Wk вращат = 21 I ω 2 .
Если тело одновременно и вращается и движется поступательно, то кинетическая энергия будет равна сумме кинетических энергий:
Wk = Wk вращат. + Wk поступ
7. Потенциальная энергия. Если на тело в каждой точке пространства действует какая-нибудь сила, то совокупность этих сил называют силовым полем или полем. Существует два вида полей — потенциальные и непотен- циальные (или вихревые). В потенциальных полях на тела, помещенные в них, действуют силы, зависящие только от координат тел. Эти силы полу- чили название потенциальных или консервативных. Они обладают свойст-
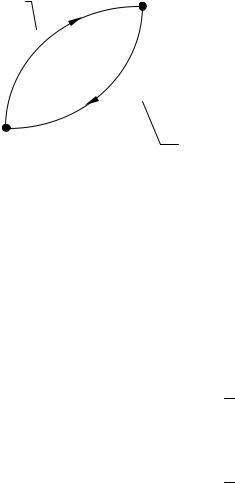
вом: работа потенциальных сил при перемещении тела по произвольному замкнутому пути (1-2-1, рис.6 ) равна нулю. Это возможно лишь в том случае, если на одних участках силы совершают положительную, а на дру- гих ¾ отрицательную работу ( рис. 6 ), а их алгебраическая сумма равна нулю. Или другими словами: работа потенциальных сил не зависит от пути переноса тела и определяется только его начальным и конечным по- ложением.
7
В макромире имеется всего лишь три вида потенциальных сил ¾ гра- витационная, упругая и электростатическая силы. К непотенциальным си- лам относятся силы трения, называемые диссипативными.
Тела, находящиеся в потенциальном поле, обладают способностью в
|
|
|
определенных |
условиях |
||
Работа на |
|
|
совершать работу. На- |
|||
2 |
|
пример, |
тело |
поднятое |
||
участке 1-2 |
|
над Землей, когда его от- |
||||
|
|
|||||
A |
|
|
пускают, |
приходит |
в |
|
|
|
движение под действием |
||||
|
|
|
||||
-A |
|
|
гравитационной |
силы, |
||
|
|
совершая работу. Следо- |
||||
|
|
|
вательно |
тела в данном |
||
1 |
|
Работа на |
поле обладают энергией, |
|||
|
которую |
называют |
по- |
|||
|
|
участке 2-1 |
||||
|
|
тенциальной. Эта энергия |
||||
|
|
|
||||
Рис 6 |
|
|
зависит от расположения |
|||
|
|
тел, создающих поле, и от |
||||
|
|
|
||||
|
|
|
положения тела |
в этом |
||
поле, т.е. она зависит от взаимного расположения взаимодействующих тел.
Энергия, обусловленная взаимодействием тел или частей одного и того же тела, называется потенциальной.
Для деформации сжатия или растяжения (рис. 3) потенциальная энергия равна:
Wp = 21 k x 2 ,
для деформации кручения (если применить аналогию п.6):
Wp = 21 D ϕ 2 .
Величина потенциальной энергии тела может быть определена лишь с точностью до произвольной постоянной, значение которой зависит от вы- бора так называемого нулевого уровня, т.е. положения тела, в котором по- тенциальную энергию условно принимают за ноль. Потенциальная энергия равна той работе, которую совершают силы поля, действующие на тело, при переносе его из данной точки на нулевой уровень. Таким образом по- тенциальная энергия тела зависит от выбора нулевого уровня. Это, однако, не отражается на физических законах, поскольку в них фигурирует либо разность потенциальной энергии тела, либо производная от этой энергии по координатам, которые не зависят от произвольной постоянной. Для уп-
8

ругих деформаций потенциальная энергия обычно берется равной нулю, в недеформированном состоянии.
8. Закон сохранения механической энергии. Величину W, равную сумме кинетической и потенциальной энергии тела, т.е. W = Wk + Wp , на-
зывают полной механической энергией или механической энергией.
В механической системе, в которой действуют только потенциальные силы, механическая энергия — величина постоянная. В этом и состоит закон сохранения механической энергии.
W = Wk + Wp = const
БАЛЛИСТИЧЕСКИЙ МАЯТНИК
Крутильный маятник представляет собой массивное тело, подвешен- ное на тонкой упругой струне. В данном случае - это жестко закрепленные с нитью два уравновешенных плеча с подвижными грузами m0 (рис 7). Ес- ли повернуть маятник на некоторый угол ϕ, то нить будет деформирована, как на рис. 3 (деформация кручения). При этом возникнут силы упругости, стремящиеся вернуть маятник в исходное положение. Если не препятство- вать, то маятник начнет двигаться. При этом запасенная потенциальная энергия, обусловленная кручением подвеса, будет переходить по закону сохранения энергии в кинетическую энергию вращения. Далее, подобно тому, как это происходит в любом маятнике, кинетическая энергия начнет переходит в потенциальную и так далее. Возникнут колебания. Для нахож- дения периода (времени одного колебания) крутильного маятника прове- дем аналогию с колебанием груза массой m на пружине жесткостью k, пе-
риод которого определяется по формуле
T = 2π 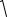
 mk .
mk .
Если заменить (см. п. 6 и 7) массу m на момент инерции I, а жесткость пру- жины k − на постоянную определяющую упругие свойства подвеса D, то период колебаний крутильного маятника запишется в виде:
T = 2π 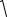
 DI .
DI .
Это выражение указывает простой путь для вычисления D, если известен момент инерции I − достаточно измерить период колебаний маятника
9
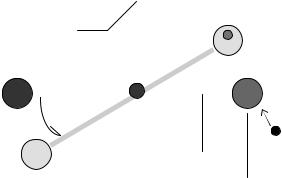
|
|
|
|
|
|
|
|
|
|
|
D = |
4π |
2 |
|
I |
(1). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подвес |
|
|
|
|
|
|
|
T 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Затухание крутильного маятни- |
|||||||||
|
m0 |
|
|
|
|
|
|
|
||||||||
|
О |
|
|
|
|
|
|
ка обычно мало, и это делает его |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
υ |
удобным прибором для измере- |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
ϕmax |
|
|
|
mO |
|
ния различных физических вели- |
||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
R |
|
m |
чин. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Баллистический маятник − |
|||||
|
|
|
|
|
|
|
|
это разновидность крутильного |
||||||||
|
|
|
|
|
l |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
маятника, когда он выводится |
|||||
|
|
|
|
Рис 7 |
|
|
из положения равновесия осуще- |
|||||||||
|
|
|
|
|
|
ствляется под |
|
действием |
ко- |
|||||||
роткого импульса внешней силы
(от столкновения с летящей “пулей”) (рис 7). Цель данной работы заключа- ется в определении скорости пули при помощи баллистического маятника, поэтому рассмотрим следующую задачу: пуля массой m, имея скорость υ,
ударяется о маятник (Рис.7) и застревает в нем на расстоянии l от оси. Как связан максимальный угол отклонения маятника от положения рав-
новесия ϕmax со скоростью пули υ ?
Согласно закону сохранения момента импульса, момент импульса сис- темы маятник-пуля до соударения равен моменту импульса системы после удара:
Lмаятн + Lпули = L'маятн + L'пули
На момент столкновения Lмаятн=0, так как угловая скорость маятника рав- на нулю, а момент импульса пули равен Lпули=mlυ (см. п. 5), так как в некотором приближении пулю можно принять за материальную точку.
После соударения L'маятн = I маятнω ' маятн и L'пули = Iпулиω 'пули .
Поскольку после удара пуля и маятник движутся вместе, то их угло- вые скорости равны, то есть: ω’маятн=ω’пули=ω’ . В итоге
mlυ = ω ' (I маятн + Iпули ) .
Условия эксперимента таковы, что I маятн >> Iпули , т.е. моментом инерции
Iпули пули можно пренебречь по сравнению с моментом |
инерции I маятн |
маятника и записать: |
|
mlυ = ω '×I маятн , |
(2) |
10
