matan-vvedenie-v-fiziku

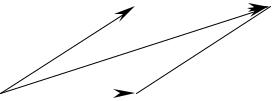
ОСНОВЫ ВЕКТОРНОГО ИСЧИСЛЕНИЯ

Вектором называется количественная характеристика, имеющая не только числовую величину, но и направление. Иногда говорят, что вектор это направленный отрезок.

Векторная система обозначений имеет двасущественныхпреимущества.

1.Формулировки физических законов в векторной форме не зависят от выбора осей координат. Векторная система обозначений представляет собой такой язык, в котором формулировки имеют физическое содержание даже без введения системы координат.

2.Векторная система обозначений является компактной. Многие физические законы выражаются через векторные величины.

Определим основныеоперации, которыеможнопроизводитьсвекторами.

Равенство двух векторовG

Два вектора aG и b равны, если они имеют одинаковую абсолютную величину и одинаковое направление. Можно сравнивать два вектора, определенные в разных точках пространства и в разные моменты времени. Параллельный перенос не меняет значения вектора.

а направление либо совпадает с начальным вектором, либо противоположно.

1

cG = d aG | c |=| d | | a | вектор c сонаправлен с вектором aG, если d > 0 (по-

ложительно) и направлен противоположно если d < 0 (отрицательное). Произведение числа 0 на любой вектор дает нулевой вектор, который по

сути таковым не является ибо он не имеет длины она равна “нулю” и не имеет направления в пространстве. Сумма двух векторов равна нулю тогда и только тогда, когда они равны по модулю и противоположны по направ-

лению. Если k – число, то k ( aG +b ) = k aG + k b т. е. умножение вектора на скаляр дистрибутивно.

Произведение векторов

Известны два вида произведений двух векторов, широко используемые в физике. Для обоих видов произведений векторов выполняется распределительный (дистрибутивный) закон умножения: произведение вектора c

на сумму aG+ b равно сумме произведений c на a и c на b . одно из этих произведений представляет собой скаляр, другое вектор.

2

длин векторов aG и b на синус угла между ними a b sin( α) направление

вектора cG определяется правилом правой руки (правого винта) от первого

G G G G

вектора ко второму. Векторное произведение не коммутативно a ×b = −b ×a .

Векторы в декартовой системе координат

Выражение физических законов в векторной форме отличается изяществом и лаконичностью. Однако бывает полезно перейти от векторов к определенным системам координат, из которых наиболее удобной является прямоугольная декартовая система координат.

Декартова система координат определяется заданием любой правой

Любой вектор считается заданным тройкой чисел ( ax ,ay ,az ) в данной

системе координат.

Найдем скалярное произведение двух векторов в декартовой системе координат, воспользовавшись естественными равенствами:

Для квадрата вектора aGимеем

aG2 = ax2 +a2y +az2 .

Векторное произведение единичных векторов равно:

i ×i = j × Gj =Gk ×k G= 0 , i × j = k , j ×k = i , k ×i = j , j ×i = −k , k × j = −i , i ×k = − j ,

поэтому векторное произведение двух векторов равно:

3

Эквивалентная запись векторного произведения через определитель:

1.1Определите проекции на оси ОX и OY векторов представленных на рисунке 1.

Пример: ax = 2м; ay =3м

1.2Запишите векторы представленные на рисунке 1 в декартовойG системе координат (через единичные орты осей ОX и OY i и j ).

Пример: a = 2 i +3 j

4

1.3 Найдите сумму векторов с рисунка 1 графически и аналитически:

а) aG+b ; б) aG+cG ;в) cG+d ; г) d +l ; д) b + f ; е) c +e ; ж) m +o ; з) p +t ; и) e +u ; к) r + s ; л) m + r ; м) n + s ; н) u +e ; о) f + aG.

Пример:

t + n = (−1 i +3 j ) +(1 i + 4 j ) = (−1+1) i +(3 + 4) j = 0 i +7 j = 7 j

1.4 Найдите разность векторов с рисунка 1 графически и аналитически:

а) aG−b ; б) a −c ;в) cG−d ; г) d −l ; д) b − f ; е) c −e ; ж) m −o ; з) p −t ; и) e −u ; к) r −s ; л) m −r ; м) n −s ; н) u −e ; о) f −aG .

Пример:

t −n = (−1 i +3 j ) −(1 i + 4 j ) = (−1−1) i +(3 −4) j = −2 i −1 j

1.5 Определите скалярное произведение двух векторов с рисунка 1

а) aG b ; б) a c ;в) cG d ; г) d l ; д) b f ; е) c e ; ж) m o ; з) p t ; и) e u ; к) r s ; л) m r ; м) n s ; н) u e ; о) f aG.

Пример: t n = (−1 i +3 j ) (1 i + 4 j ) = (−1) (1) +(3) (4) =11

1.6 Определите векторное произведение двух векторов с рисунка 1

а) aG×b ; б) a ×c ;в) cG×d ; г) d ×l ; д) b × f ; е) c ×e ; ж) m ×o ; з) p ×t ; и) e ×u ; к) r ×s ; л) m ×r ; м) n ×s ; н) u ×e ; о) f ×aG .

Пример:

t ×nG = (−1 i +3 j ) ×(1 i + 4 j ) = (−1) (4) k +(3) (1) (−k ) = −7 k

5

Приложение 2

ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Если функция f имеет в точке x производную, то существует предел:

говорят, что функция f дифференцируема в точке если ее приращение ∆y в этой точке можно записать в виде (2), где А – некоторая константа, не зави-

сящая от ∆x, но вообще говоря зависящая от x. Если функция f имеет в точ-

ке x производную, то она дифференцируема в этой точке ( А= f ' ( x ) ). Верно

и обратное утверждение: если функция дифференцируема в точке x, т. е. ее приращение в точке x представимо в виде (2), то она имеет производную в точке x равную А.

рядка, при малых ∆x можно считать ∆y равным главному члену.

Главный линейный член приращения называют дифференциалом функции f в точке x (соответствующим приращению ∆x независимой перемен-

ной x ) и обозначают так:

6

Отметим очевидные формулы:

d(U ±V ) =(U ±V )' dx =U' dx ±V' dx = dU ± dV d(UV ) =(UV )' dx =(VU' +UV' )dx =UdV +VdU

Производная функции от функции

Пусть задана функция от функции z = F( x ) = f ( ϕ( x )) , где y = ϕ( x ) , z = f ( y ) . При этом функция ϕ имеет производную в точке x , а функция f имеет производную в точке y . Тогда существует производная от F в точке x , равная:

F' ( x ) = f ' ( y )ϕ' ( x ) .

Таблица производных простейших элементарных функций.

1.( C )' = 0 (C = const)

2.(xa )' = a xa−1 , а – любое число

3.(loga x)' = 1x loga e , в частности (ln x)' = 1x

4.(ax )' = ax ln a , в частности, при a = e : (ex )' = ex

5.(sin x)' = cos x

6.(cos x)' = −sin x

7.(tgx)' = 12 xcos

8.(ctgx)' = −12

7

Производные и дифференциалы высшего порядка

Производная от функции f есть снова функция. Поэтому можно попытаться взять от нее производную. Полученная функция (если она существует, то называется второй производной от f ( x ) и обозначается через f " ( x ) . Таким образом, f " ( x ) =( f ' ( x ))' .

По индукции, производная f n( x ) порядка n определяется как первая производная от производной f n−1( x ) порядка (n – 1): f n( x ) =( f n−1( x ))' .

ращению) независимой переменной dx = ∆x .

Дифферециал n-го порядка от функции f в точке x , соответствующий дифференциалу независимой переменной dx = ∆x определяется по индукции:

С – некоторая постоянная, то функция F1( x ) = F( x ) +C есть также первообразная для f , потому, что

8

F1' ( x ) =( F( x ) +C )' = F' ( x ) +C' = F' ( x ) = f ( x )

Если F какая-либо первообразная от f на интервале (а, b), то возможные первообразные от f на этом интервале выражаются формулой F( x ) +C , где вместо С можно подставить любое число.

Неопределенным интегралом от непрерывной функции f на интервале

(а, b) называется произвольная ее первообразная функция. Неопределенный интеграл обозначается так:

∫ f ( x )dx иравен = F( x ) +C .

Если f1 , f2 – непрерывные на интервале (а, b) функции и А1 , и А2 –

постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:

∫( А1 f1 + A2 f2 )dx = A1∫ f1dx + A2 ∫ f2dx +C , где С – некоторая постоянная.

Таблица основных неопределенных интегралов

6.∫sin xdx = −cos x +C ;

7.∫cos xdx = sin x +C ;

9

Понятие определенного интеграла. Площадь криволинейной фигуры

Зададим на отрезке [а,b] (а и b – конечные числа) неотрицательную непрерывную функцию f ( x ) . Изобразим ее график и определим понятие пло-

резков [x j ,x j +1] (j = 0, 1, …, n–1) по произвольной точке ξj [x j ,x j +1]определим значения f ( ξj ) функции в этих точках и составим сумму:

и которая равна сумме площадей прямоугольников. Будем теперь стремить все ∆x j к нулю, причем так, чтобы максимальный (самый большой) частичный отре-

зок разбиения стремиться к нулю. Если при этом величина Sn стремиться к определенному пределу S , не зависящему от способов разбиения и выбора точек ξj . Тогдавеличину S назовемплощадьюнашейкриволинейнойфигуры. Т. о.:

Отвлекаясь от операции нахождения площади, будем рассматривать эту

10