Дискретная математика

1

ВВЕДЕНИЕ

Теория игр – это теория математических моделей принятия оптимальных решений в условиях неопределенности, противоположных интересов различных сторон, конфликта. Матричные игры могут служить математическими моделями многих простейших конфликтных ситуаций из области экономики. Теория игр применяется в вопросах борьбы фирм за рынки, в явлениях олигополии, в планировании рекламных компаний. При формировании цен на конкурентных рынках, в биржевой игре, в анализе коалиционного поведения возникает необходимость выбора наилучшей стратегии поведения.

С позиций теории игр можно рассматривать вопросы централизации и децентрализации управления производством, оптимальное планирование по нескольким показателям. Планирование в условиях неопределенности, порождаемой, например, техническим прогрессом, преодоление ведомственных противоречий и другие вопросы могут решаться с помощью матричных игр.

Основная цель этого методического пособия состоит в том, чтобы помочь студентам самостоятельно изучить построение математических моделей конфликтных ситуаций и познакомиться с методами решения возникающих в этих ситуациях задач.

Вметодических указаниях изложены основные теоретические вопросы, разобраны постановка и решения типичных задач, возникающих в реальной жизни и экономике. Студентам следует обратить внимание на равновесные ситуации, использование смешанных стратегий, графическое решение матричных игр. Не менее важно познакомиться с так называемыми “играми с природой”, играми с ненулевой суммой.

Систематизировать полученные знания и закрепить их практическое значение помогут задачи для самостоятельной работы.

Вконце пособия приведен список литературы, который полно и подробно отражает основные вопросы теории игр и ее использования.

2

МАТРИЧНЫЕ ИГРЫ

Игра – модель реальной конфликтной ситуации, анализ которой ведется по определенным правилам.

Матричные игры позволяют выработать наилучшую в данных условиях линию поведения, руководствуясь которой можно обеспечить себе максимально возможный средний выигрыш.

Игровые методы предназначены для обоснования решений в условиях неопределенности, которая означает неполноту, неясность тех данных, на основе которых должно приниматься решение.

Рассмотрим виды матричных игр, основываясь на различных принципах:

по числу игроков: с двумя, тремя и более участниками, возможны также игры с бесконечным числом игроков;

по числу стратегий: конечные и бесконечные игры;

по свойствам функций выигрыша: игры с нулевой суммой, или антагонистические игры, когда выигрыш одного участника равен проигрышу другого, игры с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков, наконец, игры с постоянной разностью, в которых игроки выигрывают и проигрывают одновременно;

по возможности предварительных переговоров: кооперативные и некооперативные игры.

1. Матричные игры двух участников с нулевой суммой

Если выигрыш одного участника равен проигрышу другого, то такую игру принято называть игрой с нулевой суммой, так как выигрыш каждого отличается только знаком.

Рассмотрим игру размерностью m n. Пусть заданы стратегии игроков и платежная матрица. При определении наилучших стратегий основным принципом является предположение, что противники одинаково разумны и делают все, чтобы добиться цели. Найдем наилучшую стратегию первого игрока, для чего последовательно проанализируем его стратегии.

3

Выбирая стратегию Ai , первый игрок ожидает, что второй игрок ответит стратегией B j , такой, которая минимизирует вы-

игрыш первого игрока.

Таким образом, найдем минимальное число aij в каждой

Тогда, – величина гарантированного выигрыша, который может обеспечить себе первый игрок, называется нижней ценой игры (максимином).

Второй игрок заинтересован в уменьшении своего проигрыша, или в уменьшении выигрыша первого игрока. Следовательно, выбор своей наилучшей стратегии он строит от обратной предпосылки.

Обозначим j max aij , тогда покажет максимальный

i

проигрыш второго игрока при выборе им j-ой стратегии. Пусть

min j min max aij . Стратегия второго игрока, обеспечи-

j j i

вающая ему минимальный проигрыш , называется минимаксной стратегией и показывает гарантированную величину проигрыша независимо от поведения первого игрока.

Заметим, что .

Существуют игры, в которых .

5

Значит, в матрице есть седловая точка, решение будет устойчивым, т. е. оно не зависит от того, знают или нет конкуренты намерения противников.

Задача разрешима в чистых стратегиях.

Лучшая стратегия для A – продвижение на рынок товара вида A2 , он сможет реализовать не менее 70 единиц товара.

Лучшая стратегия для B – выбор товара B2 , так как его конкурент A при этом реализует только 70 единиц, не более.

Пример 2. Найти решение матричной игры.

Решение. Найдем нижнюю и верхнюю цены игры. Получаем игру с несколькими седловыми точками 50.

Игра имеет 4 пары чистых стратегий: ( A1, B2 ); ( A1, B4 ); ( A3, B2 ); ( A3, B4 ) .

Пример 3. Между двумя государствами A и B в течение 30 дней ведется военный конфликт. Для бомбардировки моста, принадлежащего стране B, страна A использует два имеющихся у нее самолета, которые могут быть сбиты двумя зенитками страны B. У каждой из стран есть две стратегии:

A1 – послать самолеты по разным маршрутам;

A2 – послать самолеты по одному маршруту;

B1 – поместить зенитки на разных маршрутах;

B2 – поместить зенитки на одном маршруте.

Известно, что одна зенитка наверняка сбивает только один самолет, если самолет доберется до цели, то мост будет уничтожен. Найти решение этой игры.

6

Решение. По условию задачи составим матрицу игры, элементами которой служат вероятности того, что мост будет сбит

Проведем анализ игры на наличие седловой точки. Нижняя цена игры max min aij 0,5.

ij

Верхняя цена игры min max aij 1.

ji

Седловой точки нет, так как , решение надо искать в смешанных стратегиях графическим способом.

Пусть p – вероятность того, что государство A будет применять стратегию A1 , а (1 – p) – вероятность применения стратегии A2 , тогда составим уравнения прямых линий

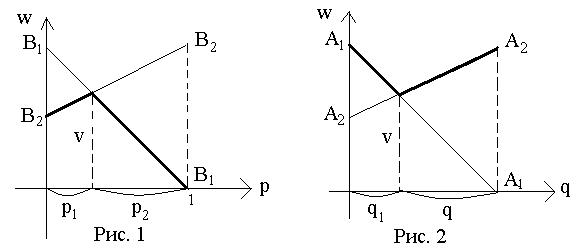
1 0 p 1 1 p p 1 ; 2 1 p 0,5 1 p 0,5 p 0,5. Графики этих прямых представлены на рис. 1. Нижняя оги-

бающая выделена на этом рисунке ломаной полужирной линией, точка максимума нижней огибающей лежит на пересечении двух прямых линий.

7

Для определения оптимальной смешанной стратегии игрока

B подставим в уравнение a11q a12 1 q a21q a22 1 q соответствующие значения из матрицы игры

0 q (1 q) q 0,5 (1 q) 1,5 q 0,5.

На рис. 2 изображены соответствующие прямые линии, выделена верхняя огибающая граница, точка пересечения соответствует минимаксу.

Это означает, что если страна A будет случайным образом посылать самолеты по разным маршрутам в течение десяти дней из тридцати, а по одному маршруту – в течение двадцати дней, то в среднем она будет иметь 66,7% удачных вылетов. Если страна B будет случайным образом помещать зенитки по разным маршрутам в течение десяти дней из тридцати, а по одному маршруту – в течение двадцати дней, то в среднем она не позволит бомбить мост чаще, чем в 66,7% случаев.

2. Правило доминирования

Это правило основано на отбрасывании тех чистых стратегий платежной матрицы, которые не вносят никакого вклада в искомые оптимальные смешанные стратегии. При этом первоначальная матрица заменяется матрицей меньших размеров.

Говорят, что i строка доминирует j строку, если

Применяя правило доминирования, используем следующий алгоритм решения матричной игры.

1. Проводим проверку наличия или отсутствия равновесия в чистых стратегиях, при наличии равновесной ситуации указыва-

8

ем соответствующие оптимальные стратегии игроков и цену игры.

2.Осуществляем поиск доминирующих стратегий и усечение матрицы.

3.Ищем цену игры и оптимальные смешанные стратегии.

Пример 4. Решить игру, заменив матрицей меньших размеров данную матрицу выигрышей:

Решение. Первая строка совпадает с последней строкой, они дублируют друг друга, последнюю строку можно вычеркнуть. Первая строка доминирует вторую, поэтому вторую строку можно отбросить. В полученной матрице четвертый столбец доминирует третий. В результате получится матрица

Проведем анализ игры на наличие седловой точки. Нижняя цена игры равна (–1), верхняя цена игры равна 0. Седловой точки нет. Решение надо искать в смешанных стратегиях графическим способом.

Запишем уравнения прямых линий, используя формулы wk a1k p a2k 1 p , k 1, 2, , n.

Получим следующие уравнения:

w1 p 2 1 p 3 p 2 ; w2 0 p 1 p p 1 ;

w3 p 2 1 p 3 p 2 .

Построим графики в системе координат pOw (рис. 3), на каждой из прямых линий определяем и отмечаем наименьшие значения, выделяем их ломаной полужирной линией, называемой нижней огибающей семейства.

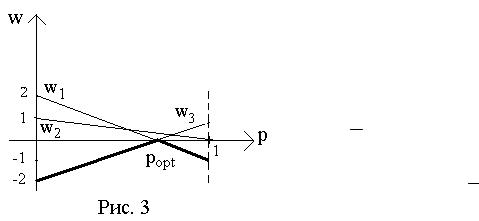
9

Пересекая прямые, образующие нижнюю огибающую, решим уравнение

3 p 2 3 p 2 , получим

2 . Цена игры 3

3 popt. 2 3 2 2 0 . 3

Для нахождения оптимальной смешанной стратегии второго игрока обратим внимание на то, что активными стратегиями являются третья w3 и первая w1, значит, используем уравнение a13q a11 1 q a23q a21 1 q ,

3. Игры с ненулевой суммой

До сих пор рассматривались игры, в которых интересы игроков были прямо противоположны. В игре с ненулевой суммой интересы игроков хотя и не совпадают, но уже и не обязательно противоположны. Поэтому поведение игроков становится более разнообразным. В игре с ненулевой суммой становится желательным как-то координировать свои действия с партнером или каким-то способом влиять на его действия.

Игры с ненулевой суммой могут быть некооперативными и кооперативными. В некоторых играх игроки принимают решение независимо друг от друга либо потому, что осуществление со-