
Дискретная математика
.pdf10
глашения невозможно, либо потому, что оно запрещено правилами игры.
Выигрыши игроков могут быть представлены двумя матрицами, поэтому такие игры получили название биматричных.
Есть два способа описания игр:
позиционный способ: с развернутым представлением игры в виде графа последовательных шагов;
нормативный способ: с представлением совокупности стратегий игроков и платежных матриц.
В примерах 5 и 6 обращается внимание только на способы описания биматричных игр, а в примере 7 решение игры разбирается полностью.
Пример 5. Дилемма узников. Два узника находятся в предварительном заключении по подозрению в совершении преступления. Каждый из узников имеет по две стратегии: признаться в преступлении и не признаться в преступлении совместно с сообщником. Адвокаты каждого обещают в случае признания одного добиться освобождения своего подзащитного и доказательства вины компаньона и наказания его сроком на пять лет. Если сознаются оба, то получают по три года, если ни один не сознается, то получают по одному году. Описать игру.
Решение. По условию задачи сговор между участниками запрещен, значит, это некооперативная игра.
Представим стратегии игроков и их платежные матрицы
|
B1 |
B2 |
|
|
B1 |
B2 |
A1 |
3 |
0 |
|
A1 |
3 |
5 |
A2 |
5 |
1 |
|
A2 |
0 |
1 |
Объединяя в одну матрицу, получим |
|
|||||
|
|
B1 |
|
B2 |
|
|
A1 |
(3, |
3) |
(0, |
5) |
|
|
A2 |
(5, |
0) |
(1, |
1) |
|
|
Представим игру в виде дерева
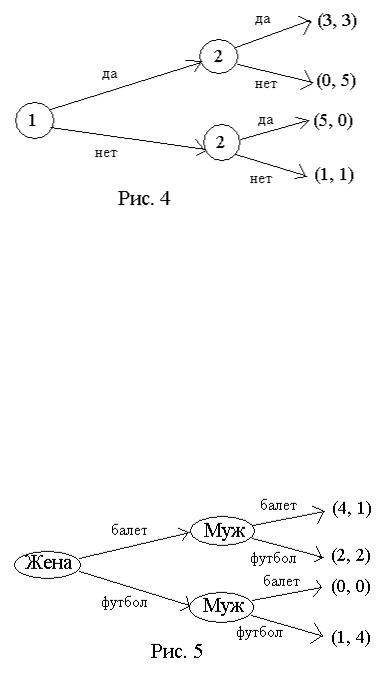
11
Пример 6. Семейный спор. Жена и муж каждый выходной решают проблему проведения досуга в городе с двумя видами развлечений: балетом и футболом. Жена получает максимум удовольствия, если идет с мужем на балет, проведя вечер с мужем на футболе, она в целом будет удовлетворена ситуацией. Муж недолюбливает балет, но присутствие жены скрашивает тягостное времяпровождение. Посещая любимые зрелища в одиночку, супруги получают половину удовольствия. Описать игру.
Решение. Представим игру в виде дерева
Запишем стратегии игроков и их платежные матрицы |
|
|||||||
|
B1 |
B2 |
|
B1 |
B2 |
|
|
|
A1 |
4 |
2 |
A1 |
1 |
2 |
|
|
|
A2 |
0 |
1 |
A2 |
0 |
4 |
B1 |
B2 |
|
|
|
|
|
|
|
|||
Объединяя в одну матрицу, получим A1 |
(4, 1) |
(2, |
2) |
|||||
|
|
|
|
|
A2 |
(0, 0) |
(1, |
4) |
12
Пример 7. Фирмы A и B производят однородный товар, который могут сбыть на одном из двух рынков. Фирма B является более состоятельной. Фирмы выбирают один из рынков независимо друг от друга. Если фирмы выберут один и тот же рынок, то в конкурентной борьбе A потерпит поражение. Если фирмы выберут разные рынки, то фирма A, не встречая противодействия, захватит выбранный рынок и выиграет больше на более удобном рынке. Найти параметры равновесной ситуации, если платежные матрицы игроков имеют вид:
10 |
2 |
5 |
2 |
|
||
A |
|
; |
B |
|
|
. |
|
1 |
|
|
1 |
1 |
|
|
1 |
|
|
|||
Решение. Для того чтобы пара (p, q) определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств:
p 1 Cq 0, |
|
|
|
p Cq 0, |
|
|
|
|
q 1 Dp 0, |
|
|
|
q Dp 0, |
|
|
|
|
|
0 p 1, |
|
|
0 q 1, |
|
|
|
|
где |
C a11 a12 a21 a22 , |
a22 a12 , |
|
D b11 b12 b21 b22 , |
b22 b21. |
Рассчитаем коэффициенты:
Ca11 a12 a21 a22 10 2 1 1 14;
a22 a12 1 2 3;
Db11 b12 b21 b22 5 2 1 1 9;
b22 b21 1 1 2.
Полученные значения подставим в две системы неравенств
p 1 14q 3 0, |
q 1 9 p 2 0, |
|||
|
p 14q 3 0, |
|
|
q 9 p 2 0. |
|
|
|
||
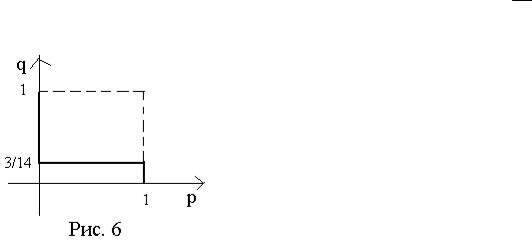
Рассмотрим сначала первую систему неравенств для трех |
||||
различных случаев: p 1, |
p 0, |
0 p 1. |
||
13
Для первого случая p 1 получим:
p 1 14q 3 0 14q 3 0 0,
p 14q 3 0. Из второго неравенства находим:
14q 3 0 |
|
q |
3 |
. |
|
||||
Для второго случая p 0 |
14 |
|
||
получим: |
||||
p 1 14q 3 14q 3 0,
0 14q 3 0 0. Из первого неравенства находим:
14q 3 0 |
|
q |
3 |
. |
|
|
|||||
|
|
|
14 |
|
|
Для третьего случая 0 p 1 получим |
|||||
p 1 14q 3 0, |
|
|
|
||
|
p 14q 3 0. |
|
|
|
|
|
|
|
|
||
Отсюда |
находим |
14q 3 0, |
14q 3 0 . Выполнение этих |
||
двух неравенств одновременно возможно лишь при q 3 . 14
Полученные результаты изображены на рис. 6. Часть зигзага, которая попала в единичный квадрат, выделена полужирной линией.
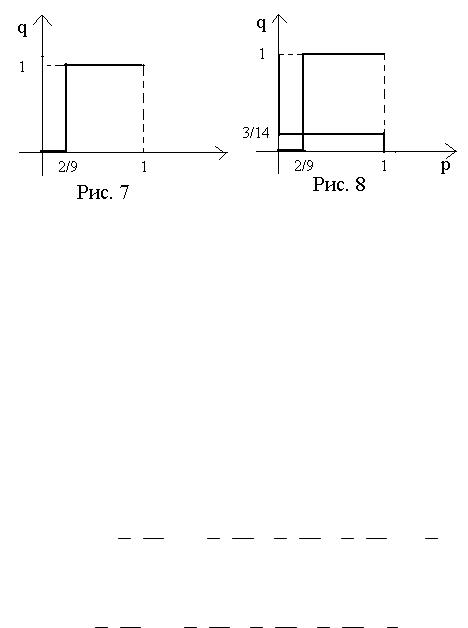
Рассмотрим теперь вторую пару неравенств для трех различ-
ных случаев |
|
|
q 1, |
q 0, |
0 q 1. |
Для первого случая q 1 получим:
q 1 9 p 2 0 9 p 2 0 0,
|
9 p 2 0. |
|
|
14 |
|
|
|
|||||
Из второго неравенства находим: |
|
|
|
||||||
9 p 2 0 |
p |
2 |
. |
|
|
|
|||
|
|
|
|
||||||
|
9 |
|
|
2 |
|
||||
Для второго случая имеем: q 0, |
p |
, а для третьего |
|||||||
|
|||||||||
|
|
2 |
|
|
|
9 |
|
||
случая 0 q 1 |
p |
. Полученные результаты изображены на |
|||||||
|
|||||||||
|
9 |
|
|
|
|
|
|
||
рис. 7. Так же как и в предыдущем случае, получили зигзаг, выделенный полужирной линией.
Результаты объединения представлены на рис. 8.
Точкой равновесия является общая точка построенных зигза-
гов. |
2 |
|
3 |
|
||
|
|
|
||||
Ее координаты равны |
|
, |
|
|
. |
|
9 |
14 |
|||||
|
|
|
||||
Тогда смешанные стратегии игроков имеют вид
|
|
|
|
2 |
|
7 |
|
|
|
|
|
|
3 |
|
11 |
|
||||
p |
|
|
|
q |
|
|
||||||||||||||
opt. |
|
|
, |
|
|
, |
opt. |
|
|
|
, |
|
|
|
. |
|||||
9 |
9 |
14 |
14 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Определим средние выигрыши игроков:
E( A, p, q) a11 pq a12 p 1 q a21 1 p q a22 1 p 1 q
10 2 3 2 2 11 7 3 7 11 4 , 9 14 9 14 9 14 9 14 7
E(B, p, q) b11 pq b12 p 1 q b21 1 p q b22 1 p 1 q
5 2 3 2 2 11 7 3 7 11 1 . 9 14 9 14 9 14 9 14 3
15
4. Игры с природой
Игра с природой – это парная матричная игра, в которой сознательный игрок A (статистик) выступает против участника, совершенно безразличного к результату игры, называемого природой.
Эти игры обладают некоторыми особенностями по сравнению с рассмотренными парными матричными играми. При их решении достаточно найти оптимальное решение только для статистика A, так как природа в рекомендациях не нуждается. Природа не противодействует игроку, может показаться, что статистическая игра проще стратегической игры. На самом же деле противоположность интересов в стратегической игре снимает неопределенность. Оперирующей стороне в игре с природой легче в том отношении, что она, скорее всего, выиграет больше, чем в стратегической игре. Но ей труднее принять решение.
Пусть статистик использует стратегии A1, A2 , , Am , а природа обладает стратегиями П1, П2 , , Пn . Известна платежная матрица с элементами aij
Для анализа игры с природой используется также матрица рисков статистика. Элементы этой матрицы равны разности между максимальным выигрышем j , который он мог бы получить,
достоверно зная, что природа реализует состояние П j , и тем выигрышем, который он получит, используя стратегию Ai , не зная, какое состояние выберет природа.
Выбрать оптимальную стратегию игроку A помогают различные критерии, позволяющие рассмотреть ситуацию с разных сторон.
Пример 8. У сельскохозяйственного предприятия есть три участка земли: влажный A1 , средней влажности A2 и сухой A3. Один из участков необходимо засадить картофелем. Известно, что для картофеля требуется определенное количество влаги в почве. Определить, на каком участке надо посадить картофель, если известна средняя урожайность на участках в зависимости от количества осадков.

|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
П1 |
П2 |
П3 |
|
|
нормы |
норма |
нормы |
||||||
A1 |
|
250 |
200 |
100 |
|
||||
|
|
||||||||
A2 |
|
|
|
|
200 |
230 |
120 |
|
|
|
|
||||||||
A3 |
|
|
100 |
240 |
260 |
|
|||
|
|
||||||||
Решение. Составим матрицу рисков, находя максимальные значения в столбцах и вычитая из них элементы столбцов.
|
|
|
|
|
|
r1 |
r2 |
r3 |
A1 |
|
0 |
40 |
160 |
||||
|
||||||||
A2 |
|
|
|
|
50 |
10 |
140 |
|
|
||||||||
A3 |
|
|
150 |
0 |
0 |
|||
|
||||||||
Анализируя платежную матрицу и матрицу рисков, можно из одинаковых на первый взгляд ситуаций A1, П2 , A2 , П1 предпочесть ту, у которой риск меньше, то есть A1, П2 .
Допустим, что известны вероятности наступления погодных условий Q1 0,3, Q2 0,4, Q3 0,3. По критерию Байеса найдем среднее значение (математическое ожидание) выигрыша для каждой стратегии и отдадим предпочтение той стратегии, у которой среднее значение максимально.
a1 250 0,3 200 0,4 100 0,3 185 ;
a2 200 0,3 230 0,4 120 0,3 188 ;
a3 100 0,3 240 0,4 260 0,3 204 . max (185, 188, 204) = 204.
То же самое можно сделать и с рисками, выбирая стратегию с минимальным риском.
r1 0 0,3 40 0,4 169 0,3 64;
r2 50 0,3 10 0,4 140 0,3 61;
r3 150 0,3 0 0,4 0 0,3 45. min (64, 61, 45) = 45.
Значит, оптимальная стратегия по критерию Байеса для игрока – стратегия A3 , т. е. сухой участок.
17
Если нельзя предпочесть ни одно из состояний природы, то используется критерий Лапласа, основанный на равной возможности всех природных состояний, которые считаются равноверо-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
1 |
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ятными, при этом ai |
|
|
aij . |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n j 1 |
||||||||||||||
Для рассматриваемого примера получим следующие значе- |
|||||||||||||||||||||||||||||||||||||
ния: |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
550 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
л |
|
|
250 200 100 |
|
|
183,3 ; |
||||||||||||||||||||||||
a |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
|
3 |
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
л |
1 |
200 230 120 |
550 |
183,3 ; |
|||||||||||||||||||||||||||
a2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
л |
|
1 |
100 240 260 |
600 |
200 . |
|||||||||||||||||||||||||
a |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3 |
|
3 |
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
max (183,3; 183,3; 200) = 200. |
|||||||||||||||||||||||||||||||||||||
Используя риски, получим: |
|||||||||||||||||||||||||||||||||||||
|
|
|
л |
|
1 |
|
|
0 40 160 |
200 |
66,7; |
|||||||||||||||||||||||||||
|
r |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
л |
|
1 |
|
50 10 140 |
200 |
66,7; |
||||||||||||||||||||||||||
|
r |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
2 |
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
л |
|
1 |
150 0 0 |
150 |
50. |
||||||||||||||||||||||||||||
|
r |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
min (66,7; 66,7; 50) = 50.
Значит, оптимальная стратегия по критерию Лапласа для игрока – стратегия A3 , т. е. выбор сухого участка.
Критерий Вальда – критерий крайнего пессимизма. В соответствии с ним в качестве оптимальных стратегий рекомендуется выбирать те стратегии, которые обеспечивают в наихудших условиях наилучший результат
max i max min aij .
i |
i j |
|
В нашем примере |
|
|
1 min 250, 200, 100 100 ; |
2 min 200, 230, 120 120 ; |
|
j |
|
j |
3 min 100, 240, 260 ; |
max 100, 120, 100 120. |
|
j |
j |
18
По критерию Вальда лучшей стратегией является стратегия A2 , то есть выбор участка средней влажности.
Критерий Сэвиджа, как и критерий Вальда, является критерием крайнего пессимизма. Согласно ему, нужно выбирать ту стратегию, при которой в наихудших условиях величина риска минимальна.
r min max rij min 160, 140, 150 140 .
i j i
Согласно этому критерию, лучшим является участок средней влажности A2 .
Наконец, рассмотрим критерий Гурвица, критерий обобщен-
ного оптимизма или пессимизма |
|
|
||||
|
|
|
|
1 k min a |
|
, |
G max k max a |
ij |
|
||||
i |
|
j |
j |
ij |
|
|
|
|
|
|
|||
где k – коэффициент оптимизма.
При k = 0 критерий Гурвица совпадает с критерием Вальда, при k = 1 получаем критерий крайнего оптимизма. Величину k выбирают, исходя из здравого смысла, опыта и знания предмета.
Составим таблицу для нахождения значений G в зависимости
от значения k. |
|
|
|
|
|
|
|
||||||
k |
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|||
|
|||||||||||||
A1 |
|
|
115 |
130 |
145 |
160 |
175 |
190 |
205 |
220 |
235 |
||
|
|||||||||||||
A2 |
|
|
131 |
142 |
153 |
164 |
175 |
186 |
197 |
208 |
219 |
||
|
|
||||||||||||
A3 |
|
132 |
148 |
164 |
180 |
196 |
212 |
228 |
244 |
||||
|
116 |
||||||||||||
Значит, если быть более оптимистичным, то надо выбрать сухой участок A3 , если более пессимистичным, то средней влажности A2 .
5. Дерево решений
Многие задачи предполагают необходимость принятия нескольких последовательных решений, для каждого из которых определено множество состояний среды. Если имеется два или
19
более последовательных решения, то более предпочтительным является подход, основанный на построении дерева решений. Дерево решений – это графическое изображение процесса решений, в котором отражены альтернативные решения, состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.
Анализ задач с помощью дерева решений включает пять этапов:
формулировка задачи;
построение или изображение дерева решений;
оценка вероятностей состояний среды;
установление выигрышей для каждой возможной комбинации альтернатив и состояний среды;
решение задачи путем расчета ожидаемой стоимостной ценности для каждой вершины состояния среды.
Пример 10 Бизнесмен решает, какого размера секция проката видеокассет будет для него выгодна. Он может получить дополнительную информацию о том, будет ли рынок видео проката благоприятным. Эта информация обойдется ему в 3 тыс. руб. Бизнесмен считает, что информация окажется благоприятной с вероятностью 0,5. Если рынок будет благоприятным, то большая секция проката принесет прибыль 15 тыс. руб., а маленькая – 5 тыс. руб. В случае неблагоприятного рынка он потеряет 20 тыс. руб., если откроет большую секцию, и 10 тыс. руб., если маленькую. Не имея дополнительной информации, бизнесмен оценивает вероятность благоприятного рынка как 0,7. Положительный результат обследования гарантирует благоприятный рынок с вероятностью 0,9. При отрицательном результате рынок может оказаться благоприятным с вероятностью 0,4.
1.Следует ли получить дополнительную информацию?
2.Следует ли открывать большую секцию?
3.Какова ожидаемая стоимостная ценность наилучшего решения?
Решение. Строим дерево решений, рассчитываем стоимостную ценность для каждой вершины состояния среды (рис. 9). Короткими параллельными линиями отсекаем ту ветвь, которая оказы-
