
математика контр раб №2
.pdf
10
y |
|
Для |
сокращения |
изложения |
не |
||
М |
|
говорят: |
"точка, соответствующая |
||||
|
комплексному |
числу |
x i y ", |
а |
|||
|
|
говорят просто – "точка x i y ". При |
|||||
0 |
х |
этом множество всех действительных |
|||||
чисел изображается |
точками |
оси |
|||||
Рисунок 1 |
|
абсцисс, которая поэтому называется |
|||||
|
|
действительной |
осью, |
множество |
|||
|
|
чисто мнимых чисел |
i y |
точками оси |
|||
|
|
ординат, называемой мнимой осью. |
|||||
|
|
Заметим, что одна точка мнимой |
|||||
|
|
оси, а именно начало координат, |
|
||||
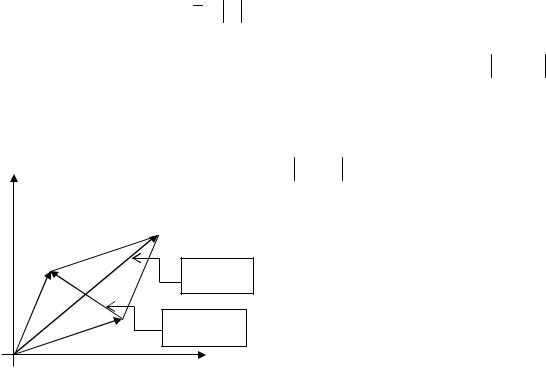
изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
Внекоторых случаях удобно считать геометрическим
изображением числа |
x i y радиус-вектор точки M(x, y) – |
O M x, y . |
|
y
0 z3
5 x
-2 z2
-5 |
z1 |
Рисунок 2
Пример 1. Построить точки
z1 5 5i , z2 2i , z3 5 .
В |
дальнейшем, наряду с |
|
представлением |
комплексных |
|
чисел |
в |
декартовых |
координатах, полезно иметь их
представление |
в обобщенных |
|||
полярных координатах. |
|
|||
Рассмотрим |
|
число |
x i y , |
|
которому |
на |
плоскости |
||
соответствует |
|
точка |
M(x, y) . |
|
Ее координаты |
в полярной |
|||
системе координат , .
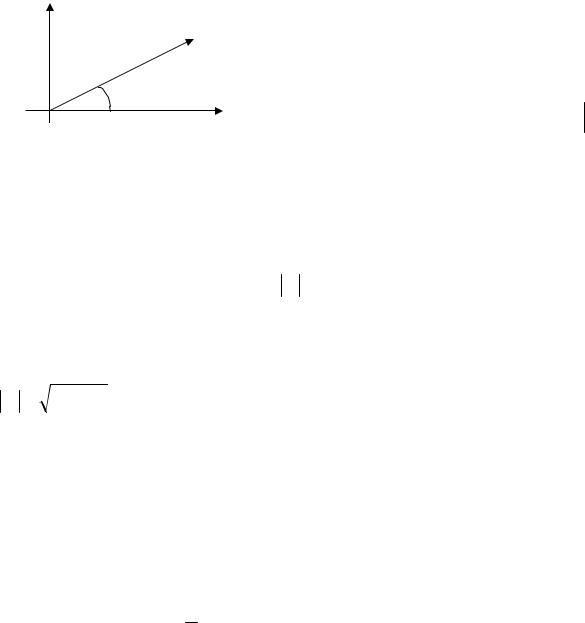
11
Тогда |
x cos , |
y |
y sin . |
M(x; y) |
|
ρ
φ
0
Рисунок 3
Полярный угол числа и обозначается
|
z x i y cos i sin |
|||||
|
cos i sin . |
|||||
x |
Полярный радиус |
|
||||
OM |
||||||
|
называется модулем |
|||||
|
комплексного числа и |
|||||
|
обозначается |
|
z |
|
. |
|
|
|
|
||||
называется аргументом комплексного
Arg z . Тогда
z cos i sin z cos Arg z i sin Arg z .
Эта форма называется тригонометрической формой
комплексного числа.
Модуль комплексного числа определяется однозначно:
z 
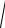 x2 y2 .
x2 y2 .
Аргумент комплексного числа определяется с точностью до слагаемого, кратного 2 . Главным значением аргумента называется значение, заключенное в интервале , . Обозначается оно arg z . Таким образом, arg z .
Очевидно, Arg z arg z 2k .
Главное значение аргумента определяется однозначно.
Так как tg arg z y ,
|
|
x |
|
|
|
|
y |
|
|
x, y I, IV четвертям, |
|
arctg |
|
, |
если |
||
x |
|||||
|
y |
|
|
x, y II четверти, |
|
|
|
|
|||
arg z arctg |
|
, |
если |
||
x |
|||||
|
|
|
x, y III четверти. |
||
|
y |
|
|
||
arctg |
|
, |
если |
||
x |
|||||
|
|
|
|
Тригонометрическая форма комплексного числа будет иметь вид

12
z z cos arg z 2k i sin arg z 2k .
Пример 2. Написать в тригонометрической форме комплексное число z 1 i .
Решение. |
z |
|
1 1 |
2, tg 1, |
y
|
|
arg z arctg 1 |
|
|
3 |
. |
||||||||
z |
1 |
|
|
|||||||||||
|
|
|
|
|
|
4 |
|
4 |
|
|||||
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
-1 |
z |
2 |
cos |
|
2k |
i sin |
|
2k |
||||||
|
|
|||||||||||||
0 |
|
|
|
4 |
|
|
|
|
4 |
|
|
|
||
x
.
Рисунок 4 |
|
|
|
|
|||||||
Пусть |
z x i y |
|
z |
|
cos Arg z i sin Arg z . Используя формулу |
||||||
|
|
||||||||||
Эйлера |
cos i sin ei , |
|
получаем |
так |
называемую |
||||||
показательную форму записи комплексного числа: |
|
||||||||||
|
|
|
|
|
z |
|
z |
|
ei Arg z . |
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3. Представить в показательной форме комплексное
число z 1 i . |
Решение |
y |
-1 0
x
z |
1 1 2, |
tg 1, |
arg z 3 ,
44
|
|
|
|
|
3 |
i 2k i |
|
z |
-1 |
1 i |
2 e |
||||
4 |
. |
||||||
|
Рисунок 5 |
|
|
|
|
|
|
Пример 4. Вычислить e i . |
|
|
|
|
|
||
Решение. По формуле Эйлера e i |
cos i sin 1 . |
||||||
13
3.2. Алгебраические действия над комплексными числами.
Для выполнения алгебраических действий над комплексными числами (№ 91-120) необходимо проработать литературу: [1, т. 1, гл. VI, Â 3, с. 137, 138; 3, т.2, Â 5.3, с. 239-244], где содержатся теоретический материал и практические рекомендации по данной теме.
Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов с учетом i i 1. При записи результата следует отделить действительную часть от мнимой части, т. е. собрать отдельно члены, содержащие множитель i , и члены, не содержащие множитель i :
x1 i y1 x2 i y2 x1 x2 i y1 y2 ,
x1 i y1 x2 i y2 x1 x2 y1 y2 i x1 y2 y1 x2 ,
x1 i y1 x2 i y2 x1 x2 i y1 y2 .
В частности, z z z 2 . Операции сложения и вычитания сводятся к сложению и вычитанию векторов, изображающих эти числа. Отсюда расстояние между точками z1 , z2 z1 z2 .
Пример 5.
y
z z0 R – уравнение окружности с центром в точке z0
z1
z1+z2
z2
z1–z2
0 |
x |
Рисунок 6
и радиусом равным R . Деление на комплексное
число, отличное от нуля, определяется как действие, обратное действию умножения.

14
Для представления частного в виде Re z i Im z
следует провести простые преобразования, показанные на следующем примере.
Пример 6. |
3 |
|
i |
|
|
3 |
i |
|
1 2i |
|
3 |
|
6i |
|
i |
|
2 1 |
|
7i |
1 |
7 i . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 2i |
|
1 2i 1 2i |
|
|
|
1 4 |
|
|
|
|
5 |
|
5 |
|
5 |
|
||||||||||
Для модуля и аргумента произведения и частного справедливы следующие утверждения:
1. |
z1 z2 |
|
z1 |
|
z2 |
, Arg z1 z2 Arg z1 Arg z2 . |
Пример 7. Найти модуль и аргумент произведения z i .
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
Решение. |
z i |
|
z |
, |
Arg z i Arg z |
|
2k . |
|
2 |
||||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
Таким образом, умножение на i соответствует повороту вектора
z на угол π ;
2
2. |
z1 |
|
|
|
|
z1 |
|
|
, |
|
|
Arg |
z1 |
Arg z1 Arg z2 . |
|
|
|
|
|
||||||||||||
z2 |
|
z2 |
|
|
z2 |
||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть |
z |
|
|
|
|
z |
|
cos Arg z i sin Arg z . |
|||||||
|
|
|
|
|
|||||||||||
Тогда z2 z z z 2 cos 2 Arg z i sin 2 Arg z .
Можно доказать методом полной математической индукции, что
для любого целого |
n 0 : zn |
|
z |
|
n cos n Arg z i sin n Arg z |
|
|
(формула Муавра). Формула справедлива и для целых отрицательных n .
15
Пример 8. Вычислить 
 3 i 5 .
3 i 5 .
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
2, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
3 |
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arg |
|
|
|
|
i arctg |
|
|
|
1 |
|
|
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
z |
3 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|||
|
|
|
|
|
|
Рисунок 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 i |
2 |
cos |
|
|
|
|
2k |
i sin |
|
|
2k |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||||
|
|
3 i |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
cos |
|
|
|
10k |
i sin |
|
|
|
10k |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
6 |
6 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 16i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
32 |
|
|
|
|
i |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Корнем n - ой степени из комплексного числа называется такое число w , для которого wn z .
Используя формулу Муавра, получим
|
|
|
|
|
|
|
|
|
Arg w |
Arg z |
|
arg z 2k |
, |
|
w |
|
n |
|
z |
|
, |
k 0, 1, 2, ... , n 1. |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для других значений k аргументы будут отличаться от полученных на число кратное 2 , и, следовательно, получатся значения корня, совпадающие с рассмотренными ранее. Итак, корень n - ой степени из комплексного числа имеет n различных значений.
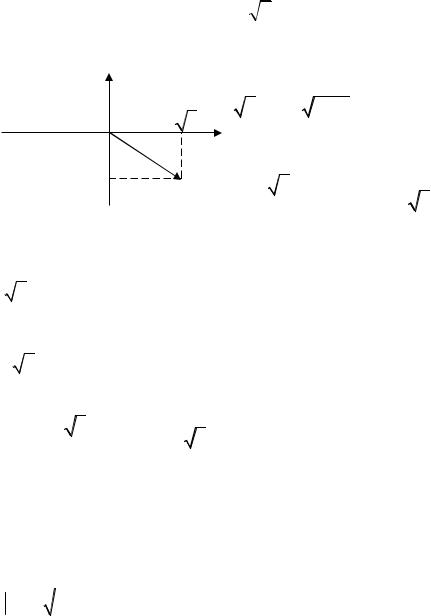
Пример 9. |
|
16 |
|
|
|
|
|
|
|
|
|
|
|||||
Найти все значения 3 |
|
|
|
и построить их. |
|
||||||||||||
8 |
|
||||||||||||||||
|
|
y |
w1 |
Решение. |
|
8 |
|
8, |
arg 8 , |
|
|
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
8 8 cos 2k i sin 2k , |
||||||||||||||
|
|
|
|
||||||||||||||
|
|
φ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
2 |
|
|
|
2k |
|
2k |
, |
|||||||||
|
|
||||||||||||||||
|
|
|
3 8 2 cos |
|
|
|
|
|
i sin |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
w3 |
|
|
|
3 |
3 |
|
|
||||||||
Рисунок 8
|
|
|
|
|
|
|
|
1 |
||||
k 0, w |
1 |
2 |
|
cos |
|
i sin |
|
|
2 |
|
|
i |
|
|
|
||||||||||
|
|
|
3 |
|
3 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
3
1 i 3 , 2
|
|
|
|
|
|
2 |
2 |
|
1 i 0 2 , |
||||||||||||||||
k 1, |
w2 |
2 |
cos |
|
|
|
i sin |
|
|
|
|
2 |
|||||||||||||
3 |
3 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
4 |
|
4 |
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
k 2, |
w |
3 |
2 |
|
cos |
|
|
|
i sin |
|
|
|
|
2 |
|
|
i |
|
|
|
1 i 3 . |
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3 |
|
|
3 |
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||
4.Обыкновенные дифференциальные уравнения
Взадачах № 91-120 при отыскании общего решения дифференциального уравнения первого порядка следует использовать литературу [2, т. 2, гл. VI, Â 3, 4, с. 161 - 166; 4, п. 12.5-12.8, с. 169-277].
Перед решением задач нужно определить тип уравнения и метод решения, при этом можно руководствоваться табл.1.
Пример. Найти общее решение уравнения |
y |
|
y . |
||||||||||||||
sin x |
|||||||||||||||||
|
|
|
dy |
|
|
|
|
|
|
|
|
|
dy |
|
|||
Так как y |
, |
то получаем уравнение |
|
y sin x – |
|||||||||||||
|
|
||||||||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|||
уравнение первого типа. Разделяем переменные |
|
|
|
||||||||||||||
|
dy |
sin x dx, |
dy |
sin xdx, ln |
|
y |
|
cosx c, |
|||||||||
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
где c – произвольная постоянная. Можно оставить решение в таком виде или выразить y в явном виде

17
y e cos x c .
y
Пример. Найти общее решение уравнения y e x y .
x
Это уравнение второго типа, однородное, следовательно,
делаем подстановку |
y |
u, y ux, y u x u . Уравнение примет |
|||||||||||||||||||
|
|||||||||||||||||||||
вид |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eu |
|
||
|
u x u eu u, |
|
|
du |
x eu , |
du |
|
|
|
. |
|||||||||||
|
|
dx |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx x |
|||||||||
Получили уравнение с разделяющимися переменными |
|||||||||||||||||||||
|
du |
|
dx |
, |
|
|
du |
|
|
dx |
, |
e u ln |
|
x |
|
ln c . |
|||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
eu |
|
x |
|
|
eu |
|
|
x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь мы обозначили произвольную постоянную не c , а lnc для удобства записи
e u ln |
|
cx |
|
, |
u |
y |
e |
|
|
||||||
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||
y x
ln cx .
Можно оставить решение в таком виде, а можно y выразить явно
|
y |
|
|
|
|
y |
|
1 |
|
|
y |
|
|
1 |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
e x ln |
cx |
, |
e x ln |
, |
|
ln ln |
, |
y x ln ln |
|
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
cx |
|
|
x |
|
cx |
|
|
|
cx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример. Найти общее решение уравнения y |
2y x . |
|
||||||||||||||||||
Это линейное |
уравнение |
P x 2, |
Q x x |
(табл.1). Делаем |
||||||||||||||||
подстановку |
y u x v x , |
y u v uv . |
|
Подставив |
эти |
|||||||||||||||
соотношения в исходное уравнение, получаем u v uv 2uv x . Одну из функций находим из уравнения
uv 2uv 0, |
dv |
2v 0 , |
|
||
|
dx |
|
тогда вторая функция u определяется из уравнения u v x . Решая первое уравнение, находим функцию v , то есть
dv |
2v, |
dv |
2dx, |
|
dv |
2dx, |
ln |
|
v |
|
2x, |
v e 2x , |
|
|
|
||||||||||||
|
|
|
|||||||||||
dx |
v |
|
v |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
18
Таблица 1 Дифференциальные уравнения первого порядка
Тип |
Вид уравнения |
Метод решения |
|||||||||||
дифференциального |
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения первого |
|
|
|
|
|
|
|
|
|
|
|
|
|
порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.С разделяющимися |
|
dy |
f1 x f2 y |
|
|
|
dy |
f1 x dx |
|||||
|
dx |
f2 y |
|||||||||||
переменными |
|
|
|
|
|
|
|
|
|||||
2. Однородное |
|
dy |
y |
Подстановка |
|||||||||
|
|
|
f |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dx |
x |
|
u, y ux , |
|
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
приводит к |
||||
|
|
|
|
|
|
|
y u x u |
||||||
|
|
|
|
|
|
уравнению первого типа |
|||||||
3. Линейное |
|
dy |
P x y Q x |
Подстановка |
|||||||||
|
|
dx |
|
|
|
|
y u x v x |
|
|||||
|
|
|
|
|
|
приводит к уравнениям |
|||||||
|
|
|
|
|
|
первого |
типа |
||||||
|
|
|
|
|
|
|
dy |
|
P x v 0, |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dx |
|
|
||||
|
|
|
|
|
|
|
du |
v Q x |
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
dx |
|
|
||||
произвольную константу для функции v полагаем равной нулю. Получаем уравнение для нахождения функции u
|
du |
e 2x |
x, |
|
du |
x |
dx, |
du x e2xdx, |
|
du x e2xdx, |
||||||||||
|
|
e 2x |
||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
u |
1 |
x e2x |
1 |
|
e2xdx |
1 |
x e2x |
1 |
e2x c . |
||||||||
|
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
4 |
|
||||||
Решение исходного уравнения имеет вид |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
y uv |
|
|
xe2x |
|
|
e2x |
c |
e |
2x . |
|||||||
|
|
|
|
|
|
4 |
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
При решении задач № 121-150 используются приёмы решения дифференциальных уравнений второго порядка с постоянными
19
коэффициентами, изложенные в литературе [2, т. 2, гл. VI, Â 8, 9, с. 186 - 197; 4, п. 12.11-12.13, с. 279-286].
Для нахождения общего решения однородного дифференциального уравнения используется табл. 2, а для нахождения частного решения неоднородного дифференциального уравнения используется табл. 3.
Пример. Найти частное решение дифференциального уравнения
|
|
|
y 8y 16y 2xe 4x , |
|
|
||
удовлетворяющее начальным условиям y 0 1, |
y 0 2. |
||||||
|
|
Таблица 2. Общее решение однородного уравнения |
|||||
Вид |
общего |
решения |
Корни |
характеристического |
|||
однородного уравнения |
уравнения |
|
|
||||
1. |
y0 |
c1ek1x c2ek 2x |
|
k1 ,k 2 |
– вещественные, k1 k 2 |
||
2. |
y0 |
(c1 c2x)ekx |
|
k1 ,k 2 |
– вещественные, k1 k 2 |
||
3. |
y0 |
c1 cos x c2 sin x e x |
k1 ,k 2 |
– комплексные, |
|||
|
|
|
|
k1 i, |
k 2 i |
||
Решение. Общее решение неоднородного уравнения можно
записать в виде y y0 Y , где y0 |
– общее решение однородного |
|||||
уравнения |
|
y 8y 16y 0 , |
|
|
||
|
|
|
|
|
||
которое |
определяется |
по табл. 3, а |
Y – |
частное решение |
||
неоднородного уравнения, которое определяется по табл. 4. |
||||||
Для определения y0 составим характеристическое уравнение |
||||||
|
|
|
k 2 8k 16 0 . |
e 4x (c1 c2x) . |
||
Его корни k1 k 2 4 . Следовательно, y0 |
||||||
Так |
как |
правая |
часть |
уравнения |
f x 2xe 4x , то |
|
Y x2 e 4x Ax B . |
|
|
|
|
||
Здесь a 4, |
Pn x 2x, |
r 2 . |
|
|
|
|
|
|
|
Y e 4x Ax3 Bx2 . |
|
||
