
Инженерная графика.Задачник
.pdfРекомендации по выполнению задания
Лист 1
По заданным в варианте размерам вычерчиваю две проекции только той криволинейной поверхности, которая рассечена заданной плоскостью.
Заданные плоскости – проецирующие, следовательно, решение ведется на основе алгоритма решения позиционных задач на пересечение геометрических образов, когда один из них проецирующий (см. с. 35, 36):
1.Путем анализа определяют проецирующий образ и его вырожденную проекцию.
2.На вырожденной проекции проецирующего образа находят одну из проекций общего элемента (линии пересечения).
3.Строят другую проекцию общего элемента, отнеся его к образу общего положения.
Таким образом, задача сводится к построению плоской ли-
нии на поверхности. Чтобы построить линию на поверхности необходимо построить достаточное количество точек этой линии как точки принадлежащие поверхности.
Точка принадлежит поверхности, если она лежит на линии принадлежащей поверхности. В качестве таких линий следует брать прямые и окружности.
Пересечение сферы с плоскостью
Любая плоскость пересекает сферу по окружности. Однако эти окружности проецируются на плоскости проекций в виде эллипса, и только, если они лежат в плоскости уровня, в окружности.
Для построения точек на поверхности сферы через имеющуюся проекцию точек M2, N2 следует проводить вырожденную проекцию вспомогательной окружности расположенной в плос-
71

кости уровня (отрезок прямой). Строят другую проекцию этой окружности (окружность с радиусом равным расстоянию от оси
Рис. 5.1
сферы до очерковой образующей). На полученной проекции вспомогательной окружности будут лежать искомые проекции
72
точек M1, N1 (рис. 5.1). Если точка лежит на очерковой образующей сферы (С2, D2), то другая ее проекция лежит на экваторе (C1, D1) . Если же точка лежит на экваторе (E2, F2), то другая ее проекция лежит на очерковой образующей (E1, F1). Построив достаточное количество таких точек, получим проекцию эллипса. Малая ось эллипса определяется отрезком C1D1. Положение и величина большой оси эллипса определятся точками А2, В2, А1, В1.
Пересечение конической поверхности с плоскостью
Замечательным свойством конической поверхности является то, что на ней представлены все возможные кривые второго порядка.
Рассекая конус плоскостями того или иного направления, мы получим (рис 5.2):
1 – эллипс, если секущая плоскость пересекает все образующие конуса на конечном расстоянии;
2 – окружность как более частный случай эллипса;
3 – точку как случай вырождения эллипса; 4 – параболу, если секущая плоскость параллельна одной из
образующих конуса; 5 – прямую, если секущая плоскость проходит через обра-
зующую конуса (точнее пару совпавших прямых); 6 – гиперболу, если секущая плоскость параллельна двум
образующим конуса; 7 – две пересекающиеся прямые, если секущая плоскость
проходит через эти образующие (через вершину конуса).
Для построения проекций точек на поверхности конуса через имеющуюся проекцию точки проводят его образующие (прямые или окружности). Строят проекции этих образующих, а на них проекции точек.
Для построения проекций линии на поверхности конуса необходимо построить достаточное количество точек этой линии как точки принадлежащие поверхности конуса.
73
7 6
5
4
2
3
1
Рис. 5.2
Рассмотрим пример построения эллипса на поверхности ко-
нуса.
Начнём с построения точек 1 и 2, лежащих на очерковых образующих конуса (рис. 5.3). Для построения этих точек не нужно дополнительно проводить образующие конуса, т. к. можно использовать сами очерковые образующие. Точки 3 и 4 легко построить на профильной проекции, а затем перенести на горизонтальную. Воспользуемся тем свойством, что они расположены симметрично по отношению к осям конуса и их ординаты на плоскостях π1 и π3 равны.
74
 43
43
 31
31
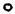 41
41
Рис. 5.3
Для построения точек 5 и 6 (рис. 5.4), проведём через них окружность. Построим её горизонтальную проекцию, и на ней построим горизонтальные проекции этих точек. Профильные проекции точек найдём на основании известного свойства о равенстве ординат.
75
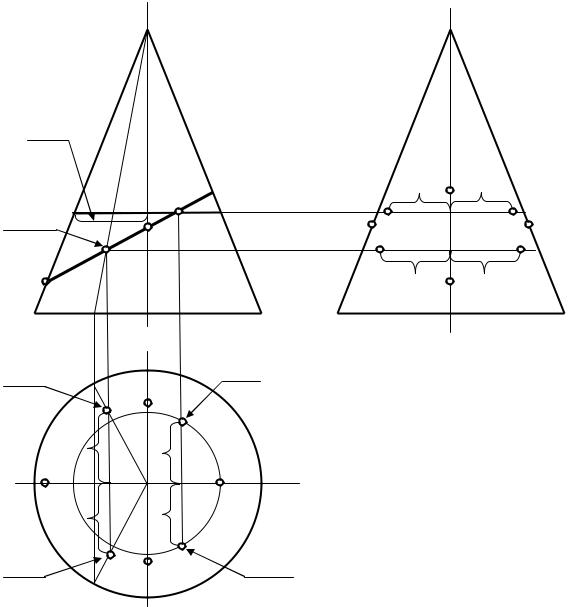
Точки 7 и 8 можно построить подобно точкам 5 и 6. Можно получить проекции этих точек, проведя через них вспомогательные прямые (рис. 5.4). На горизонтальных проекциях этих прямых строим горизонтальные проекции этих точек, а по ним профильные.
R
52≡62 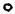
72≡82 |
53 |
63 |
|
73 83
71 |
51 |
81 |
61 |
R – радиус вспомогательной окружности
Рис. 5.4
76

Для получения проекций кривой, полученные точки соединяем с учётом видимости на проекциях (рис. 5.5).
Рис. 5.5
Аналогичные построения позволяют построить на поверхности конуса гиперболу и параболу.
Пересечение цилиндрической поверхности с плоскость
В сечении цилиндра плоскостью линии пересечения могут быть:
1– эллипс, если секущая плоскость не параллельна и не перпендикулярна к образующим цилиндра.
77

Рис. 5.6
78
2 – окружность, если секущая плоскость перпендикулярна к образующим (оси вращения) цилиндра.
3 – две образующие, если секущая плоскость параллельна образующим (оси вращения).
Определение натуральной величины фигуры сечения
На рис. 5.6 секущая плоскость рассекает конус по гиперболе. Плоская фигура сечения ограничивается гиперболой и прямой линией АВ, по которой секущая плоскость пересекает основание конуса.
Для построения натуральной величины фигуры сечения, вводим новую плоскость проекций параллельно секущей плоскости и перпендикулярно горизонтальной плоскости проекций, т. е. преобразуем плоскость фигуры в плоскость уровня. Из имеющихся точек построения на кривой проведем линии связи перпендикулярно к новой оси проекций. По линиям связи от новой оси отложим высоты этих точек, взяв их на второй проекции. Полученные точки соединим. Построенная таким образом плоская фигура будет равна ее натуральной величине.
Лист 2
Построение линий пересечения поверхностей во многом зависит от положения заданных геометрических образов в пространстве. Различают задачи в которых один из заданных образов проецирующий по отношению к плоскостям проекций и задачи в которых оба заданных образа общего положения.
Если один из образов проецирующий, задача решается на основании ранее названного алгоритма (см. с. 35, 36, 71).
Если оба заданные образа общего положения, задача решается либо путем преобразования одного из образов в проецирующий, либо с использованием вспомогательных секущих поверхностей посредников. В качестве таких посредников берут плоскости или сферы.
Рассмотрим примеры решения задач на пересечение двух поверхностей.
79

Пример 1. Построить линию пересечения прямого кругового цилиндра со сферой (рис.5.7).
Рис. 5.7
Цилиндр занимает горизонтально проецирующее положение. Следовательно, горизонтальная проекция линии пересечения
80
