
- •1. Основные понятия
- •2. Основные задачи кинематики
- •3. Способы задания движения точки
- •Кинематика точки
- •2. Ускорение точки.
- •1. Ускорение точки (продолжение)
- •2. Частные случаи движения точки
- •1. Поступательное движение твердого тела и его свойства.
- •2. Вращательное движение твердого тела.
- •3. Частные случаи вращательного движения.
- •1. Плоскопараллельное движение твердого тела.
- •2. Скорости точек при плоскопараллельном движении.
- •1. Сложное движение точки.
- •2. Определение скоростей и ускорений точки в сложном движении.
2. Ускорение точки.
Перейдем к решению второй основной задачи кинематики точки - определению скорости и ускорения по уже заданному векторным, координатным или естественным способом движению.
Скоростью точки называется векторная величина, характеризующая быстроту и направление перемещения точки. В системе СИ скорость измеряется в м/с.
a) Определение скорости при векторном способе задания движения.
Пусть движение
точки задано векторным способом, т.е.
известно векторное уравнение (2.1):
![]() .
.

Рис. 2.6. К определению скорости точки
Пусть за время t
радиус-вектор
![]() точкиМ
изменится на величину
точкиМ
изменится на величину
![]() .
Тогда средней скоростью точкиМ
за время t
называется
векторная величина
.
Тогда средней скоростью точкиМ
за время t
называется
векторная величина
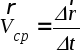 .
.
Мгновенной
скоростью (или далее - просто скоростью)
называется предел
![]() приt
стремящемся
к нулю, т.е.
приt
стремящемся
к нулю, т.е.
 .
(2.4)
.
(2.4)
Вспоминая определение производной, заключаем:
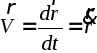 .
(2.5)
.
(2.5)
Здесь и в дальнейшем
знаком
![]() будем обозначать дифференцирование по
времени. При стремленииt
к нулю вектор
будем обозначать дифференцирование по
времени. При стремленииt
к нулю вектор
![]() ,
а, следовательно, и вектор
,
а, следовательно, и вектор![]() ,
поворачиваются вокруг точкиМ
и в пределе совпадают с касательной к
траектории в этой точке. Таким образом,
вектор
скорости равен первой производной от
радиус-вектора по времени и всегда
направлен по касательной к траектории
движения точки.
,
поворачиваются вокруг точкиМ
и в пределе совпадают с касательной к
траектории в этой точке. Таким образом,
вектор
скорости равен первой производной от
радиус-вектора по времени и всегда
направлен по касательной к траектории
движения точки.
б) Скорость точки при координатном способе задания движения.
Выведем формулы для определения скорости при координатном способе задания движения. В соответствии с выражением (2.5), имеем:
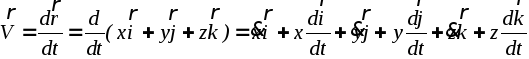 .
.
Так как производные от постоянных по величине и направлению единичных векторов равны нулю, получаем
![]() .
(2.6)
.
(2.6)
Вектор
![]() ,
как и любой вектор, может быть выражен
через свои проекции:
,
как и любой вектор, может быть выражен
через свои проекции:
![]() (2.7)
(2.7)
Сравнивая выражения (2.6) и (2.7) видим, что производные координат по времени имеют вполне определенный геометрический смысл - они являются проекциями вектора скорости на координатные оси. Зная проекции, легко вычислить модуль и направление вектора скорости (рис. 2.7):
![]() или
или
![]() ,
(2.8)
,
(2.8)
![]() ,
,
![]() ,
,![]() .
(2.9)
.
(2.9)

Рис. 2.7.К определению величины и направления скорости
в) Определение скорости при естественном способе задания движения.
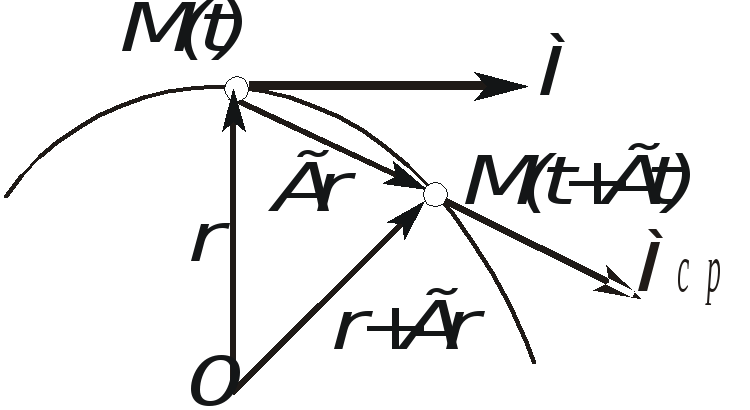
Рис. 2.8. Cкорость точки при естественном способе задания движения
Согласно (2.4)
 ,
,
где
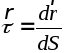 - единичный вектор касательной. Таким
образом,
- единичный вектор касательной. Таким
образом,
![]() ,
,
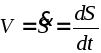 (2.10)
(2.10)
Величина V=dS/dt называется алгебраической скоростью. Если dS/dt>0, то функция S = S(t) возрастает и точка движется в сторону увеличения дуговой координаты S, т.е. точка движется в положительном направлении Если же dS/dt<0, то точка движется в противоположном направлении.
2. Ускорение точки
Ускорением называется векторная величина, характеризующая быстроту изменения модуля и направления вектора скорости. В системе СИ ускорение измеряется в м/с2.
a) Определение ускорения при векторном способе задания движения.
Пусть точка М в момент времени t находится в положении М(t) и имеет скорость V(t), а в момент времени t + t находится в положении М(t + t) и имеет скорость V(t + t) (см. рис. 2.9).
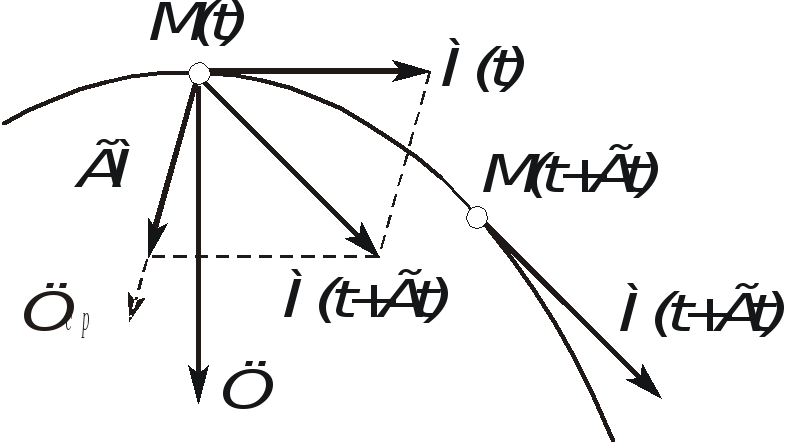
Рис. 2.9. Ускорения точки при векторном способе задания движения
Средним ускорением
![]() за промежуток времениt
называется отношение изменения скорости
за промежуток времениt
называется отношение изменения скорости
![]() кt
, т.е.
кt
, т.е.
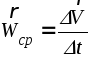 .
.
Предел
![]() приt
0 называется
мгновенным (или просто ускорением) точки
М
в момент времени
t
приt
0 называется
мгновенным (или просто ускорением) точки
М
в момент времени
t
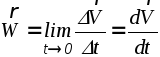 .
(2.11)
.
(2.11)
Согласно (2.11), ускорение при векторном способе задания движения равно векторной производной от скорости по времени.
б). Ускорения при координатном способе задания движения.
Подставляя (2.6) в (2.11) и дифференцируя произведения в скобках, находим:
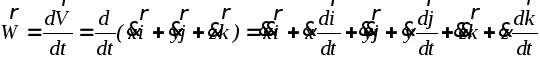 .
.
Учитывая, что
производные от единичных векторов
![]() равны нулю, получаем:
равны нулю, получаем:
![]() .
(2.12)
.
(2.12)
Вектор
![]() может быть выражен через свои проекции:
может быть выражен через свои проекции:
![]() .
(2.13)
.
(2.13)
Сравнение (2.12) и (2.13) показывает, что вторые производные от координат по времени имеют вполне определенный геометрический смысл: они равны проекциям полного ускорения на координатные оси, т.e.
![]() ,
,
![]() ,
,
![]() .
.
Зная проекции, легко вычислить модуль полного ускорения и направляющие косинусы, определяющие его направление:
![]() ,
,
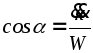 ,
, ,
,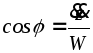 .
(2.14)
.
(2.14)
в). Ускорение точки при естественном способе задания движения
Приведем некоторые сведения из дифференциальной геометрии, необходимые для определения ускорения при естественном способе задания движения.
Пусть точка М движется по некоторой пространственной кривой. С каждой точкой этой кривой связаны три взаимно ортогональные направления (касательная, нормаль и бинормаль), однозначно характеризующие пространственную ориентацию бесконечно малого элемента кривой вблизи данной точки. Ниже приводится описание процесса определения указанных направлений.
Для того чтобы провести касательную к кривой в точке М , проведем через нее и близлежащую точку М1 секущую ММ1.
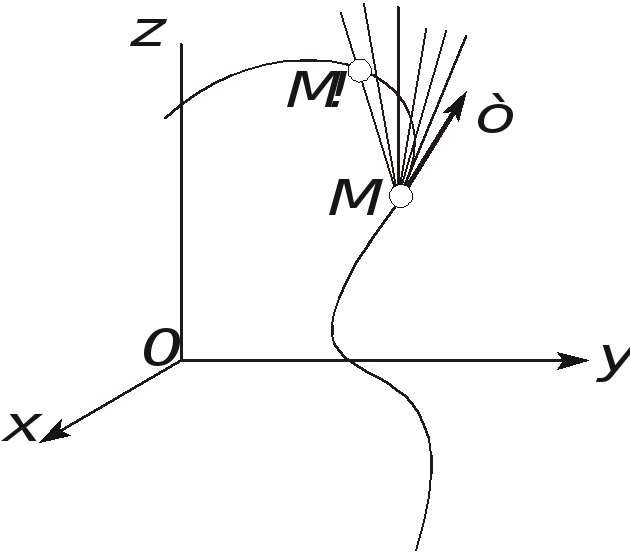
Рис. 2.10. Определение касательной к траектории движения точки
Касательная к
кривой в точке М
определяется как предельное положение
секущей ММ1
при стремлении точки М1
к точке М
(рис. 2.10). Единичный вектор касательной
принято обозначать греческой буквой
![]() .
.
Проведем единичные
векторы касательных к траектории в
точках М
и М1.
Перенесем вектор
![]() в точкуМ
(рис. 2.11) и образуем плоскость, проходящую
через эту точку и векторы
в точкуМ
(рис. 2.11) и образуем плоскость, проходящую
через эту точку и векторы
![]() и
и![]() .
Повторяя процесс образования аналогичных
плоскостей при стремлении точкиМ1
к точке М,
мы получаем в пределе плоскость,
называемую соприкасающейся
плоскостью.
.
Повторяя процесс образования аналогичных
плоскостей при стремлении точкиМ1
к точке М,
мы получаем в пределе плоскость,
называемую соприкасающейся
плоскостью.

Рис. 2.11. Определение соприкасающейся плоскости
Очевидно, что для плоской кривой соприкасающаяся плоскость совпадает с плоскостью, в которой лежит сама эта кривая. Плоскость, проходящая через точку М и перпендикулярная касательной в этой точке, называется нормальной плоскостью. Пересечение соприкасающейся и нормальной плоскостей образует прямую, называемую главной нормалью (рис. 2.12).
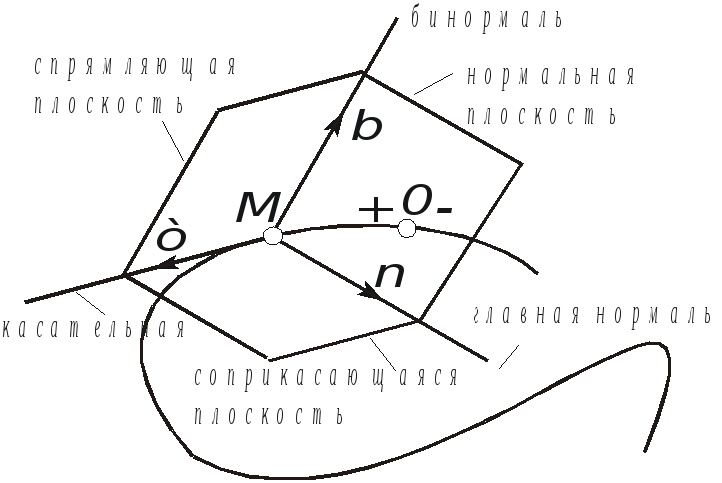
Рис. 2.12. Естественный трехгранник
Единичный вектор,
направленный вдоль главной нормали
внутрь траектории, обозначим буквой
![]() .
Единичный вектор
.
Единичный вектор![]() ,
ортогональный соприкасающейся плоскости
и направленный в ту сторону, откуда
поворот от
,
ортогональный соприкасающейся плоскости
и направленный в ту сторону, откуда
поворот от![]() ‚
к
‚
к
![]() виден
происходящим против хода часовой
стрелки, определяет направление
бинормали
виден
происходящим против хода часовой
стрелки, определяет направление
бинормали
![]() .
Плоскость, образуемая векторами
.
Плоскость, образуемая векторами![]() и
и![]() ,
называетсяспрямляющей
плоскостью.
,
называетсяспрямляющей
плоскостью.
Система координат, образуемая тремя взаимно ортогональными осями- касательной, нормалью и бинормалью, называется естественной системой координат. Трехгранник, образуемый соприкасающейся, нормальной и спрямляющей плоскостями называется естественным или подвижным трехгранником. Перемещаясь вместе с движущейся точкой М, оси этого подвижного трехгранника меняют свою ориентацию в пространстве, оставаясь взаимно ортогональными.
Пример. Движение точки М задано уравнениями
![]() ,
,
![]() ,
,
где k - постоянная.
Определить модули скорости и ускорения как функции времени.
Решение: Дважды дифференцируя уравнения движения по времени, получаем
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подставляя найденные значения производных в формулы (8) и (14), получаем:
![]() ,
,
![]() .
.
Лекция 12
Вопросы
