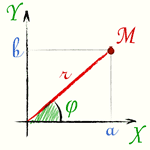Геометрическое представление сопряжённых чисел

Если комплексное число  , то число   называется сопряжённым (или комплексно сопряжённым) к   (часто обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

5.

Ко́мпле́ксная плоскость[1] — это двумерное вещественное пространство  , которое изоморфно полю комплексных чисел  . Каждая точка такого пространства — этоупорядоченная пара вида  , где   и   — вещественные числа, и где первый элемент пары соответствует вещественной части, а второй элемент пары соответствует мнимой части комплексного числа  :

		Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числаa + b·i обозначается |a + b·i|, а также буквой r. Из чертежа видно, что:
1.	r= | a+b·i |= a2+b2

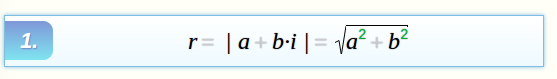
Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + b·i и a - b·i имеют один и тотже модуль.

Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + b·i, называется аргументом комплексного числа a + b·i

Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отлючающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k - любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:

Однако ни одна из этих формул в отдельности не позволяет найти аргумент. Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности, а также учитывать номер четверти, на координатной плоскости, в которой находится комплексное число.

http://clck.ru/7rVq — вычисление всего этого дела.

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту стригонометрическими функциями.

Формула Эйлера утверждает, что для любого действительного числа   выполнено следующее равенство:

,

где   — основание натурального логарифма,

 — мнимая единица.

6 и 7.

Сложение и вычитание

        По аналогии со сложением и вычитанием векторов мы приходим к следующему правилу сложения и вычитания комплексных чисел:

(a₁ + b₁i ) + (a₂ + b₂i ) +...+  (a_n + b_ni ) = (a₁ + a₂ + ...+ a_n ) + (b₁+ b₂+...+ b_n ) i = a + bi

        Операция введена, так как получили элемент того же множества.

        Вычитание определяется как действие, обратное сложению, то есть разность x + iy = (a₁ + b₁i) – (a₂ + b₂i ) определяется из условия:

(x + iy) + (a₂ + b₂i ) = (a₁ + b₁i)  .

        Из правила сложения получаем:

x + a₂ = a₁, y + b₂ = b₁.

        То есть x = a₁ – a₂,   y = b₁ – b₂ и разность

(a₁ + b₁i ) – (a₂ + b₂i ) = (a₁ – a₂ ) + (b₁– b₂) i.

Умножение комплексных чисел

        Определение. Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению  модулей сомножителей, а аргумент –  сумме аргументов сомножителей.

        Это определение совершенно очевидно, если использовать показательную форму комплексного числа:

        Пусть комплексные числа даны в алгебраической форме. Найдём их произведение: (a₁ + b₁i) (a₂ + b₂i ) = x + iy.

Имеем  .

Согласно определению умножения можем записать:

.

Распишем:       ,

,

.

Окончательно получим:

.

        Отсюда следует правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены.

        Если  z  = а + b i  –  комплексное число, то число   называется сопряжённым с числом z . Его обозначают при помощи черты над числом.

, но  , следовательно,  .

Деление комплексных чисел

.

Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.

Если делимое и делитель даны в алгебраической форме, то правило деления таково: для того, чтобы разделить комплексное число (a₁ + b₁i )  на другое комплексное число  (a₂ + b₂i ), то есть найти  , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.

.

        В результате операции получили элемент того же множества. Значит, операция деления считается введённой.

Возведение в степень комплексных чисел

        Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или в показательной форме.

1. ,

2. .

Для возведения комплексного числа в степень нужно модуль возвысить в эту степень, а аргумент умножить на показатель степени.

Извлечение корня

Определение. Корнем n -ой степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.

Из этого определения следует, что из равенства   следует равенство  .

        Из равенства комплексных чисел следует  , а аргументы отличаются на число, кратное   ;  . Отсюда  ,  . Здесь  есть арифметическое значение корня, а k  – любое целое число. Таким образом, получается формула .

В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k  = 0, 1, 2, … , n  -  1.

        Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы   и   отличаются на величину, не кратную   , и будут одинаковыми, если указанные аргументы отличаются на величину, кратную   . Поэтому разность

не может быть кратна   .  Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.

Пусть теперь k₃–  целое число, не входящее в эту последовательность подряд взятых значений k . Это число можно представить в виде k₃= gn + k_i, где g  –  целое число, а k_i –  одно из чисел этого ряда, поэтому  , то есть значению k₃ соответствует то же значение корня, что и значению k_i.

Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.

Пример 1. Решить уравнения а) x² + 25 = 0, б) x³ + 27 =0.

Решение. а)  , то есть первое уравнение имеет два мнимых корня: x₁ = 5i, x₂ = -5i;

б) воспользуемся формулой x³ + a³ = (x +a) (x² - ax + a²),  x³ + 27 = (x +3) (x² - 3x + 9). Приравнивая нулю каждый из множителей, получаем один корень действительный и два комплексных:

;

x₂ и x₃ –  сопряжённые комплексные числа.

Пример 2. Вычислить, изобразить на плоскости, записать в тригонометрической и показательной форме :  а)  ;            б) ( i )ⁱ.         

Решение. а) Сначала запишем числа в алгебраической форме, выполнив

операцию деления (см. п. Деление комплексных чисел). Домножим на сопряжённое число, и, учитывая, что i² = -1, получим:

= - 3 -  3i ;

х = Re z  = - 3, у = Jm z  = - 3, что соответствует точке на плоскости (- 3, - 3) (см рис.3).

Модуль комплексного числа:

.

        Так как точка находится в третьей четверти, то аргумент комплексного числа будет:

,

Записываем тригонометрическую и показательную формы комплексного числа:

.

б) z = i ⁱ, i  = 0 + 1 ·  i , х = Re z  = 0, у = Jm z  = 1,

.

–  действительное число (точка на оси ох) (см. рис. 4).

Пример 3. Вычислить  .

Решение. Представим число в тригонометрической (или показательной) форме, для чего найдём его модуль и аргумент:

- 1 = - 1 + 0 ·  i,   х = - 1, у = 0,

, k  = 0, 1, 2.

k  = 0,  ;

k  = 1, 

k  = 2,  .

8.

Одномерное пространство — геометрическая модель материального мира, в которой положение точки возможно охарактеризовать всего одним числом. Также одномерным пространством считается n-мерное пространство, где n=1.

Двуме́рное простра́нство (иногда говорят двухме́рное пространство) — геометрическая модель плоской проекции физического мира, в котором мы живём. Двумерным пространством считается n-мерное пространство, где n=2.

Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.

Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются еёкоординатами. В зависимости от целей и характера исследования выбирают различные системы координат.

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

Аффинная (косоугольная) система координат — прямоугольная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными неколлинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса.

• Барицентрические координаты были впервые введены в 1827 году А. Мебиусом, решавшим вопрос о центре тяжести масс, расположенных на вершинах треугольника. Они аффинно инвариантны, представляют собой частный случай общих однородных координат. Точка с барицентрическими координатами расположена в n-мерном векторном пространстве En, а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в (n−1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса.

• Биангулярные координаты — частный случай бицентрических координат, система координат на плоскости, задаваемая двумя фиксированными точками С1 и С2, через которые проводится прямая, выступающая в качестве оси абсцисс. Позиция некоторой точки P, которая не лежит на этой прямой, определяется углами PC1C2 и PC2C1.

• Биполярные координаты характеризуются тем, что в качестве координатных линий на плоскости в этом случае выступают два семейства окружностей с полюсами A и B, а также семейство окружностей, ортогональных к ним. Преобразование биполярных координат в декартовы прямоугольные осуществляется посредством специальных формул. Биполярные координаты в пространстве называются бисферическими; в этом случае координатными поверхностями являются сферы, поверхности, образуемые вращением дуг окружностей, а также полуплоскости, проходящие через ось Oz.

• Бицентрические координаты — всякая система координат, которая основана на двух фиксированных точках и в рамках которой положение некоторой другой точки определяется, как правило, степенью ее удаления или вообще позицией относительно этих двух основных точек. Системы подобного рода могут быть довольно полезны в определённых сферах научных исследований.

• Бицилиндрические координаты — система координат, которая образуется в том случае, если система биполярных координат на плоскости Oxy параллельно переносится вдоль оси Oz. В качестве координатных поверхностей в этом случае выступают семейство пар круговых цилиндров, оси которых параллельны, семейство ортогональных к ним круговых цилиндров, а также плоскость. Для перевода бицилиндрических координат в декартовы прямоугольные для трехмерного пространства также применяются специальные формулы.

• Конические координаты — трехмерная ортогональная система координат, состоящая из концентрических сфер, которые описываются посредством их радиуса, и двух семейств перпендикулярных конусов, расположенных вдоль осей x и z.

• Координаты Риндлера используются преимущественно в рамках теории относительности и описывают ту часть плоского пространства-времени, которая обыкновенно называется пространством Минковского. В специальной теории относительности равномерно ускоряющаяся частица находится в гиперболическом движении, и для каждой такой частицы в координатах Риндлера может быть выбрана такая точка отсчета, относительно которой она покоится.

• Параболические координаты — это двумерная ортогональная система координат, в которой координатными линиями является совокупность конфокальных парабол. Трехмерная модификация параболических координат строится путем вращения двумерной системы вокруг оси симметрии этих парабол. У параболических координат также имеется определенный спектр потенциальных практических приложений: в частности, они могут использоваться применительно к эффекту Штарка. Параболические координаты связаны определенным отношением с прямоугольными декартовыми.

• Проективные координаты существуют, согласно наименованию, в проективном пространстве Пn (К) и представляют собой взаимно однозначное соответствие между его элементами и классами конечных подмножеств элементов тела К, характеризующихся свойствами эквивалентности и упорядоченности. Для определения проективных координат проективных подпространств достаточно определить соответствующие координаты точек проективного пространства. В общем случае относительно некоторого базиса проективные координаты вводятся чисто проективными средствами

• Тороидальная система координат — трехмерная ортогональная система координат, получаемая в результате вращения двумерной биполярной системы координат вокруг оси, разделяющей два ее фокуса. Фокусы биполярной системы, соответственно, превращаются в кольцо с радиусом а, лежащее на плоскости xy тороидальной системы координат, в то время как ось z становится осью вращения системы. Фокальное кольцо также называют иногда базовой окружностью.

• Трилинейные координаты являются одним из образцов однородных координат и имеют своей основой заданный треугольник, так что положение некоторой точки определяется относительно сторон этого треугольника — главным образом степенью удаленности от них, хотя возможны и другие вариации. Трилинейные координаты могут быть относительно просто преобразованы в барицентрические; кроме того, они также конвертируемы в двумерные прямоугольные координаты, для чего используются соответствующие формулы.

• Цилиндрические параболические координаты — трехмерная ортогональная система координат, получаемая в результате пространственного преобразования двумерной параболической системы координат. Координатными поверхностями, соответственно, служат конфокальные параболические цилиндры. Цилиндрические параболические координаты связаны определенным отношением с прямоугольными, могут быть применены в ряде сфер научных исследований.

• Эллипсоидальные координаты — эллиптические координаты в пространстве. Координатными поверхностями в данном случае являются эллипсоиды, однополостныегиперболоиды, а также двуполостные гиперболоиды, центры которых расположены в начале координат. Система ортогональна. Каждой тройке чисел, являющихся эллипсоидальными координатами, соответствуют восемь точек, которые относительно плоскостей системы Oxyz симметричны друг другу.

 Правую и левую системы координат невозможно поворотами[3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси   против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси  , если этот поворот наблюдать со стороны положительного направления оси  ).

9.

Аффи́нное простра́нство — пространство, обобщающее аффинные свойства евклидова пространства. Во многом схоже с векторным пространством; однако для аффинного пространства, в отличие от векторного, характерно то, что все точки являются равноправными (в частности, в нём не определено понятие нулевой точки, или начала отсчёта).

Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.

Остальное не нашел (

11.

12.

13.

Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном евклидовом пространстве.

Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором.

Скаля́рное произведе́ние иногда внутреннее произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними.

Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x.

Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

14.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы.

Количество строк и столбцов матрицы задают размер матрицы.

Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Транспонированная матрица — матрица  , полученная из исходной матрицы   заменой строк на столбцы.

Формально, транспонированная матрица для матрицы   размеров   — матрица   размеров  , определённая как AT[i, j] = A[j, i].

Например,

      и      

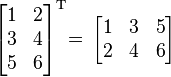
Онлайн калькулятор. Транспонирование матрицы.

http://clck.ru/92zn9

Сложение матриц сумма матриц) A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен 

с_i,j = a_i,j + b_i,j

Вычитание матриц (разность матриц) A - B есть операция нахождения матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен 

с_i,j = a_i,j - b_i,j

http://clck.ru/92znZ — сложение и вычитание матриц.

Определение. Произведением скаляра   на матрицу   называется матрица   тех же размеров, что и матрица А, где элементы   определяются равенством  , для всех значений индексов.

Обозначение:  .

Другими словами, для того, чтобы умножить матрицу на скаляр, нужно каждый элемент матрицы умножить на данный скаляр.

http://clck.ru/92zoG — умножение на скаляр.

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

http://clck.ru/8hTru — умножение матриц.

15.

16.