1.

Мно́жество — одно из ключевых понятий математики, в частности, теории множеств и логики.

Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).

Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками.

Интервал — открытый с обоих концов промежуток в упорядоченном множестве.

О́бласть — некоторая часть большей структуры, связное подмножество топологического пространства.

Число́ — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.

Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида , где и — вещественные числа, — мнимая единица; то есть . Множество всех комплексных чисел обычно обозначается от лат. Complex — тесно связанный.

Целые числа — расширение множества натуральных чисел , получаемое добавлением к нуля и отрицательных чисел.

Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел.

Действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль.

Множества, элементами которых являются точки, называются точечными множествами. Таким образом, можно говорить о точечных множествах на прямой, на плоскости, в каком-либо пространстве. Ради простоты мы ограничимся рассмотрением точечных множеств на прямой.

Примеры . http://mathhelpplanet.com/static.php?p=tochechnye-mnozhestva

2.

Линейно упорядоченное множество или цепь ― частично упорядоченное множество, в котором для любых двух элементов и имеет место или .

Важнейший частный случай линейно упорядоченных множеств ― вполне упорядоченные множества.

1. Элементы теории множеств

1. Логические символы

Квантор - заменяет выражение "для любого", "для произвольного", "для какого бы ни было".

Квантор - заменяет выражение "существует", "найдется".

Запись (импликация) означает, что из справедливости высказывания A вытекает справедливость высказывания B. Если, кроме того, из справедливости высказывания B вытекает справедливость A, то записываем  . Если  , то высказывание B является необходимым и достаточным условием для того, чтобы выполнялось высказывание A.

Если предложения A и B справедливы одновременно, то записываем  . Если же справедливо хотя бы одно из предложений A или B, то записываем  .

Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит.

Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b,c, ...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:

                  N - множество всех натуральных чисел;                   Z - множество всех целых чисел;                   Q - множество всех рациональных чисел;                   R - множество всех действительных чисел;                   C - множество всех комплексных чисел;                   Z₀ - множество всех неотрицательных целых чисел.

Запись   (или  ) означает, что элемент a принадлежит множеству A.

Запись   (или  ) означает, что элемент a не принадлежит множеству A.

3.

Вещественные числа обычно представляются в виде чисел с плавающей запятой.

Числа с плавающей запятой — один из возможных способов предсталения действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.

1. Десяти́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры  1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.

2. Двоичная система счисления — позиционная система счисления с основанием 2.

В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 510, в двоичной 1012. Иногда двоичное число обозначают префиксом0b, например 0b101.

В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012произносится «один ноль один».

3. Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами.

Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных.

Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

4. Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.

Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10v10до 15v10, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Арифметические операции в двоичной системе

Арифметические действия в двоичной системе производится по тем же правилам что и в десятичной системе счисления. Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.

Сложение двоичных чисел.

Сложение выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного сложения:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10.

При сложении необходимо помнить, что 1+1 дают нуль в данном разряде и единицу переноса в старший.

Пример 3.5. Сложить два числа:

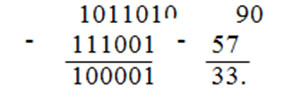
Вычитание двоичных чисел.

Вычитание выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного вычитания:

0 – 0 = 0

1 – 0 = 1

1 – 1 = 0

10 – 1 = 1.

Пример 3.6. Найти разность двух чисел:

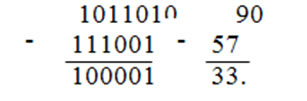
Т.е. при вычитании двоичных чисел в случае необходимости занимается 1 из старшего разряда, которая равна двум единицам младшего разряда.

Умножение двоичных чисел.

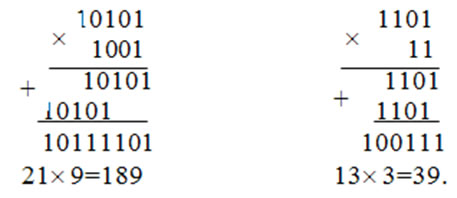
Умножение в двоичной системе производится по тому же принципу что и в десятичной системе счисления, при этом используется таблица двоичного умножения:

0 * 0 = 0

0 * 1 = 0

1 * 0 = 0

1 * 1 = 1 .

Пример 3.7. Найти произведение двух чисел:

Как видно из приведенных примеров, операция умножения может быть представлена как операции сдвига и суммирования.

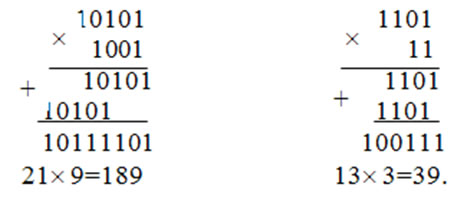
Деление двоичных чисел.

Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля.

Пример 3.8. Найти частное двух чисел если:

1. Делимое больше делителя:

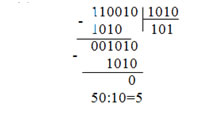
2. Делимое меньше делителя:

Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования.

http://planetcalc.ru/911/ если будут проблемы.

http://numsys.ru/

4.

Ко́мпле́ксные[1] чи́сла (устар. мнимые числа[2]) — числа вида  , где   и   — вещественные числа,   — мнимая единица; то есть  . Множество всех комплексных чисел обычно обозначается   от лат. complex — тесно связанный.

Мнимая единица — обычно комплексное число, квадрат которого равен отрицательной единице. 

1. Алгебраическая форма

Запись комплексного числа   в виде  , где   и  , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):

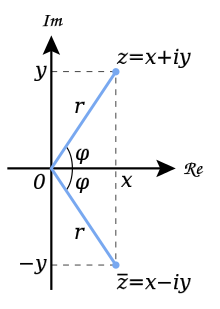
2. Тригонометрическая форма

Если вещественную   и мнимую  части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

3. Показательная форма

Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

4. Сопряжённые числа