Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Южно-Уральский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДИНАМИКА

.pdf

Скачиваний:

Добавлен:

08.05.2015

Размер:

2.24 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Вектор Q называют также главным вектором количеств движения точек механической системы.

Проекции количества движения Q на оси прямоугольной декартовой системы координат имеют вид

n	n	n	n	n
Qx mk vkx mk xk , Qy mk vky mk yk , Qz mk vkz
k 1	k 1	k 1	k 1	k 1

mk zk .

k 1

Размерность количества движения						Q	кг м	.
Размерность количества движения						Q		.
							с
Поскольку скорость центра масс механической системы равна
		n
		mk vk					n
	vc	k 1		, то		M vc mk vk ,
	vc	M		, то		M vc mk vk ,
		M					k 1
							k 1
n
где M mk	– масса системы.
k 1

Получаем			Q		M vc .		(3.1.1)

Количество движения механической системы равно произведению массы системы на скорость ее центра масс.

Проекции вектора количества движения системы на оси прямоугольной декартовой системы координат соответственно:

Qx M vCx ; Qy M vCy ; Qz M vCz .

(3.1.2)

Количество движения твердого тела может быть найдено по тем же формулам, как для механической системы.

3.2. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ

Рассмотрим движение механической системы, состоящей из Ak n мате-

риальных точек в инерциальной системе отсчета Oxyz . Силы, действующие на

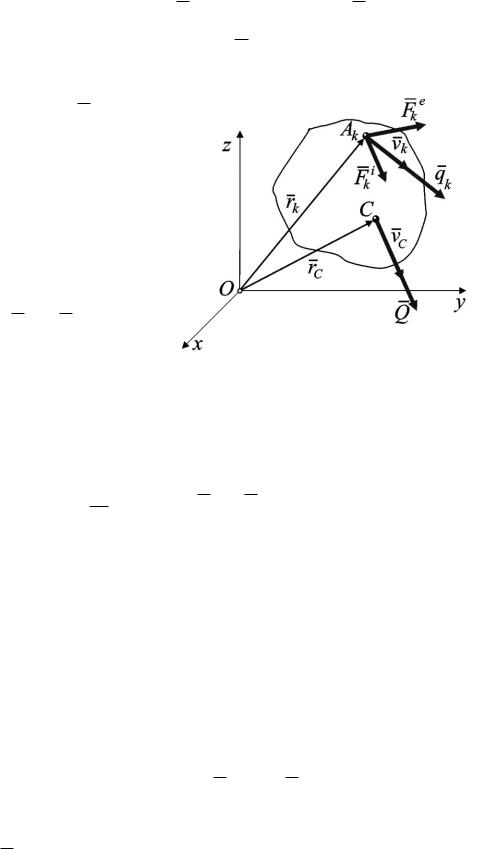
точки системы, разделим на внешние Fke n и внутренние Fki n . Пусть точка

Ak массой mk движется под действием силы Fke , являющейся равнодейству ющей внешних сил, действую-

щих на данную точку, и Fki , являющейся равнодействующей внутренних сил, действующих на данную точку, ak – ускорение точки.

В соответствии с основным законом динамики точки можем записать

mk ak Fke Fki ,

или

m		dVk F e F i .			Рис. 3.2.1

	k		k	k

		dt

Если массы отдельных точек системы остаются постоянными, то последнее выражение можно представить в виде:

dtd mk vk Fke Fki ,

или

dqk		e		i .
	F		F		(3.2.1)

dt	k		k

Уравнение (2.1) выражает теорему о количестве движения для точки в дифференциальной форме: производная по времени от количества движения

точки равна сумме сил, действующих на точку.

Записывая выражения (2.1) для всех точек системы и суммируя их, полу-

чим

n	dqk		n	n
		dQ
				Fke	Fki .
	dt	dt
k 1			k 1	k 1

n
Здесь	Fke		e – главный вектор внешних сил системы.
		U
k 1

Fki 0 , так как внутренние силы системы попарно равны и противо-

k 1

положны.

В итоге получаем


dQ		e .
dQ	U		(3.2.2)
dt	U		(3.2.2)
dt

Это теорема о количестве движения механической системы в диффе-

ренциальной форме: производная по времени от количества движения меха-

нической системы равна главному вектору внешних сил, действующих на точки системы.

Проецируя (2.2) на оси неподвижной системы координат, получим:

dQ	U e ;	dQy	U e ;	dQ	U e .
x				z

dt	x	dt	y	dt	z
dt		dt		dt

Производные по времени от проекций количества движения механической системы на оси координат равны проекциям на теже оси главного вектора внешних сил, действующих на точки системы.

Если масса всей системы M mk остается постоянной, то выраже-

k 1

ние (2.2) можно представить в виде
	dvC		e , или M a		e .
M	dvC	U		U		(3.2.3)
M		U		U		(3.2.3)
	dt		C
	dt

Уравнение (2.3) выражает теорему о движении центра масс механиче-

ской системы: центр масс механической системы движется как материальная точка с массой равной массе всей системы под действием силы, равной главному вектору внешних сил, действующих на точки системы.

Проецируя равенство (2.3) на оси координат, получаем:

mx	U e ; my		U e	; mz	U e .
C	x	C	y	C	z

Это дифференциальные уравнения движения центра масс механической системы в координатной форме.

Законы сохранения количества движения

Пусть главный вектор внешних сил, действующих на точки системы, равен нулю, т.е. Ue 0. Тогда из (2.2) следует, что


dQ
dQ	0 Q	const.	(3.2.4)
dt	0 Q	const.	(3.2.4)
dt

Равенство (2.4) выражает закон сохранения количества движения в

данном пространстве: если главный вектор внешних сил, действующих на точки системы, равен нулю, то количество движения системы остается постоянным по величине и направлению.

Для системы, масса которой постоянна, получаем закон сохранения

движения центра масс:

	e 0 M	dvC	0 v	const.
U		dvC			(2.5)
U					(2.5)
		dt	C
		dt

Если главный вектор внешних сил системы равен нулю, то скорость центра масс системы остается постоянной по величине и направлению.

Предположим, что U e 0 , но одна из его проекций, равна нулю, тогда получаем

Uxe 0 dQdtx 0 Qx const.

Для системы с постоянной массой

Uxe 0 M dvdtx 0 vx const.

Эти равенства выражают закон сохранения проекции количества движения и закон сохранения проекции скорости центра масс.

Д е й ст в и е п а р ы с и л н а с в о б о д н о е т в е р д о е т е л о

Если приложить пару сил к свободному твердому телу, то центр масс будет оставаться в покое, поскольку главный вектор пары равен нулю. Под действием пары сил тело начнет вращаться вокруг центра масс.

Пусть центр масс вращающегося тела (например, маховика) не находится на геометрической оси вращения, тогда при вращении возникают центробежные силы, стремящиеся изогнуть вал, и, передаваясь через подшипники на основание, вызывают вибрации всей машины.

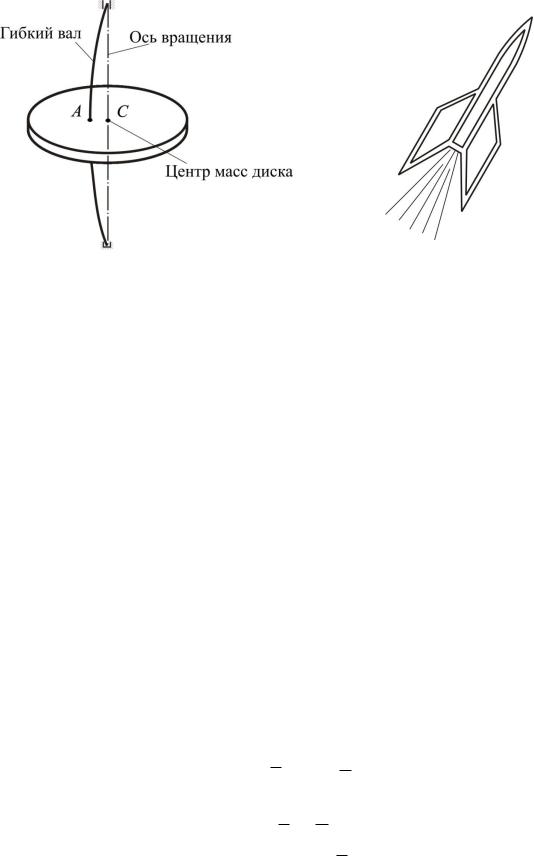
Рис. 3.2.2

Рис.3.2.3

Чтобы бороться с этим вредным, действием, шведский инженер Лаваль прибегнул к средству, кажущемуся на первый взгляд парадоксальным. Он уменьшил диаметр вала, насадив рабочее колесо паровой турбины на тонкий и гибкий вал в палец толщиной (рис. 3.2.2).

Оказалось, что колесо турбины в этом случае ведет себя как свободное твердое тело под действием пары сил, т.е. приобретает свойство самоцентрирования: при весьма большой угловой скорости вращения гибкий вал изгибается так, что центр масс колеса приближается к геометрической оси вращения.

Р е а кт и в н о е д в и ж е н и е

В реактивном снаряде газообразные продукты сгорания топлива с большой скоростью выбрасываются из сопла (рис. 3.2.3).

При отсутствии влияния сил тяжести и сил сопротивления среды и при нулевой начальной скорости, центр масс системы (ракета-топливо) остаётся на месте, а сама ракета движется вперед.

Импульс силы и теорема импульсов

Элементарным импульсом dS силы F , действующей в течение времени dt , называют вектор

dS Fdt.

Проекции элементарного импульса dS на оси прямоугольной декартовой системы координат равны:

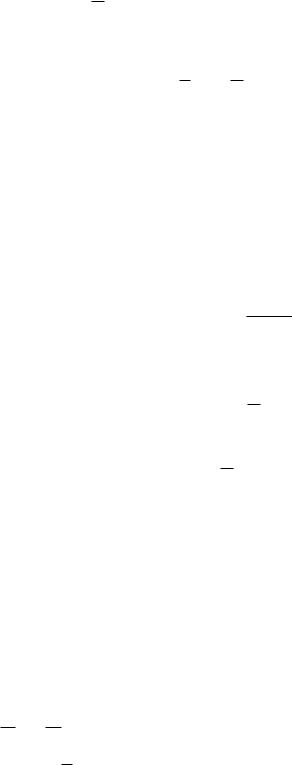
dSx Fx dt; dS y Fy dt; dSz Fz dt.

Импульсом силы F , действующей на интервале времени t0 , t , назовем вектор

S Fdt.

Проекции импульса силы на оси координат выражаются формулами

t	t	t
Sx Fxdt;	S y Fydt;	Sz Fzdt.
t0	t0	t0

Размерность импульса силы

S Н с кг м .

Запишем теорему о количестве движения в дифференциальной форме:

Fke .

k 1

Fkedt

dSke

Откуда

(3.2.6)

k 1

Таким образом, дифференциал количества движения механической

системы равен сумме элементарных импульсов внешних сил, действующих на точки механической системы.

Интегрируя (2.6) на интервале t1 , t2 , получим

n t2

dSke

или

Q2 Q1 Ske .

(3.2.7)

k 1t

k 1

Здесь Q1 и Q2 – количество движения системы в начальный и конечный моменты времени; Ske – импульс равнодействующей внешних сил, действующих на точку.

Выражение (2.7) представляет собой математическое выражение теоре-

мы об изменении количества движения механической системы в интегральной

форме или теоремы импульсов: изменение количества движения механиче-

ской системы за некоторый промежуток времени равно сумме импульсов внешних сил, действующих на точки механической системы за это время.

В проекциях на оси координат получаем:

Qx2 Qx1 Skxe ; Qy2 Qy1 Skye ; Qz2 Qz1 Skze . .

3.3.КИНЕТИЧЕСКИЙ МОМЕНТ ТОЧКИ

ИМЕХАНИЧЕСКОЙ СИСТЕМЫ

Кинетический момент точки относительно центра

Рис. 3.3.1

движения точки:

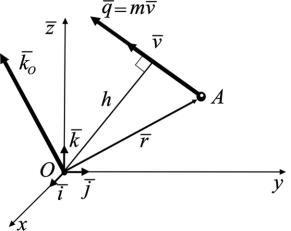
Пусть материальная точка A массой m движется со скоростью v в пространстве Oxyz (рис. 3.3.1),

qmv – количество движения точки

вэтом пространстве.

Кинетическим моментом точки относительно центра O (момен-

том количества движения точки относительно центра O) называют величину, равную векторному произведению радиус-вектора точки относительно центра на количество


	kO momO q r q r mv .		(3.3.1)

Вектор kO приложен в центре O и образует с векторами			и q правую
		r

тройку векторов. Модуль кинетического момента равен произведению количества движения на расстояние от центра до линии действия вектора скорости

(рис. 2.1).

kO q h

Кинетический момент точки относительно центра можно представить в матричной форме:

mv m

(3.3.2)

v y

Здесь x, y, z – координаты точки; vx , vy , vz

– проекции ее скорости на

оси координат.

Проекции кинетического момента на оси координат можно записать, раскрывая определитель (3.2) по элементам первой строки:

kO x m y vz z vy ; kO y m z vx x vz ; kO z m x v y y vx .

(3.3.3)

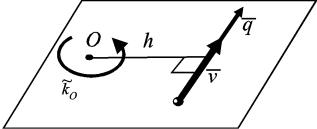
В плоскости, проходящей через центр O и вектор скорости точки, кинетический момент точки относительно центра можно рассматривать как величину алгебраическую и изображать дуговой стрелкой (рис.

3.3.2):

	~	m v h .
Рис. 3.3.2	kO	m v h .
	~
Знак	kO	берется положитель-

ным, когда кинетический момент направлен против хода часовой стрелки.

Кинетический момент точки относительно оси

Кинетическим моментом точки относительно оси назовем алгебраический момент проекции количества движения точки на плоскость перпендикулярную оси относительно точки пересечения оси с плоскостью

(рис. 3.3.3).

Величина kz считается положительной, если наблюдатель, смотрящий с конца положительного направления оси z , видит движение точки относительно оси происходящим против хода часовой стрелки.

kz momO m vП m vП hП .

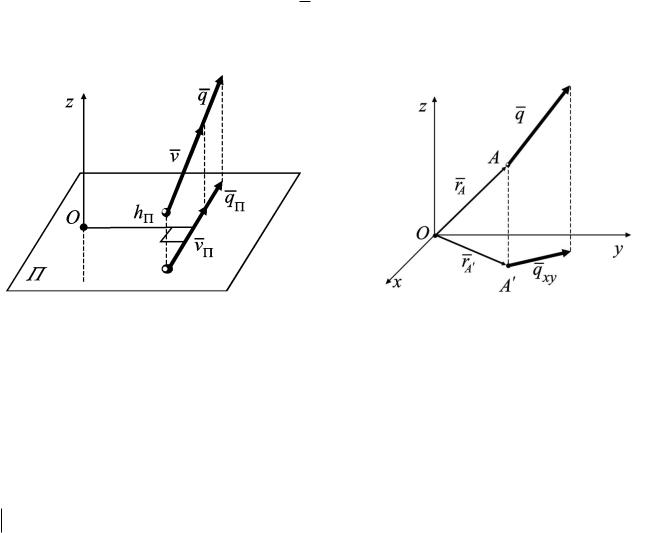
Кинетические моменты относительно центра O и оси z , проходящей через этот центр, связаны зависимостью

kz kO z .

Рис. 3.3.3

Рис. 3.3.4

Проекция кинетического момента точки относительно некоторого центра на ось проходящую через этот центр равна кинетическому моменту точки относительно данной оси.

В самом деле, модули величин в уравнении (3.3.4) равны (рис. 3.3.4):

rA qxy

qy x y qx

momO qxy

Нетрудно проверить и равенство их знаков. Теперь можем записать:

kx			ky			kz
kx	kO	;	ky	kO	;	kz	kO	.
		x			y			z

Кинетический момент механической системы

Рассмотрим движение механической системы A k n материальных точек в пространстве Oxyz .

Кинетический момент механической системы или главный момент количеств движения точек системы относительно какого-либо центра или оси –

это сумма кинетических моментов точек системы относительно того же центра или той же оси:

	n	n		n
K	O kOk momOqk rk mk vk ,				(3.3.5)
	k 1	k 1		k 1
		n	n
	Kz kzk momz qk .				(3.3.6)
		k 1	k 1

Здесь r k – радиус-вектор точки A k ; v k – ее скорость; m k – масса (рис. 2.5).

Проекции кинетического момента системы относительно центра на оси координат с началом в этом центре равны кинетическим моментам системы относительно соответствующих осей координат:

Kx ;

K y ;

Kz .

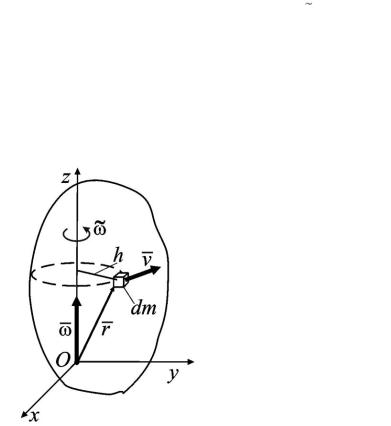
Кинетический момент твердого тела

Рассмотрим вращение твердого тела массой			M в пространстве Oxyz.
Для кинетического момента тела относительно оси Oz можем записать:
Kz momzv dm	vh dm		h2 dm Iz .
M	M	M

Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно оси вращения на алгебраическую угловую скорость.

Рис. 3.3.5

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2019459.26 Кб5Джозеф Ковелло Бизнес -планы.doc
#
16.03.201624.85 Кб25Джон Локк.docx
#
13.09.201969.97 Кб29ДЗ Финансы и кредит.docx
#
09.11.2019110.59 Кб5Дидактический материал.doc
#
21.09.2019101.89 Кб1Дизайн торговой рекламы.doc
#
08.05.20152.24 Mб12ДИНАМИКА.pdf
#
22.11.201916.03 Mб28Диплом Брыковой.doc
#
16.03.20161.78 Mб53диплом вадима2.doc
#
16.03.2016183.4 Кб128диплом на проверку.docx
#
28.08.2019139.29 Кб11Диплом НОН.docx
#
03.11.2018564.74 Кб10диплом оконч вар.doc