
ДИНАМИКА
.pdf
n
Величина M mk называется массой системы.
k 1
Точка С пространства, радиус-вектор которой
1 n
rC M mk rk k 1
называется центром масс системы.
В однородном поле тяготения центр масс совпадает с центром тяжести. Иногда центр масс называют центром инерции.
К о о р д и н а т ы ц е нт р а м а с с :
|
1 |
n |
1 |
n |
1 |
n |
|
xc |
mk xk , yc |
mk yk , zc |
mk zk . (2.1.2) |
||||
|
|
|
|||||
|
M k 1 |
M k 1 |
M k 1 |
||||
При движении системы Mk n точек центр масс будет также двигаться.
Скорость центра масс:
|
|
|
drC |
|
|
1 |
|
n |
|
||||
vC |
|
|
|
|
mk vk |
(2.1.3) |
|||||||
|
|
|
|
|
|||||||||
|
|
|
dt |
|
|
|
M k 1 |
|
|||||
Ускорение центра масс: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d vC |
|
|
|
1 |
n |
|
|||||
aC |
|
|
|
|
mk ak . |
(2.1.4) |
|||||||
|
|
|
|
|
|||||||||
|
|
|
dt |
|
|
|
M k 1 |
|
|||||
Здесь vk – скорость и ak |
– ускорение точки M k . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
|
|
|
O mk rk |
|
|||||||
Величина |
|
|
S |
|
|||||||||
k 1
называется статическим моментом механической системы относительно центра О.
n |
|
|
|
|
|
|
|
|
|
|
|
SO |
|
||||
Поскольку mk rk |
MrC , то |
|
O M rC и rc |
. |
||||
S |
||||||||
|
||||||||
k 1 |
|
|
|
M |
||||
|
|
|
|
|
|
|
||
Отсюда видно, что если центр О совпадает с центром масс, то статический момент равен нулю.
O C SO SC 0
10

Выражения
n |
n |
n |
mk xk SOyz ; mk yk SOxz ; mk zk SOyx . |
||
k 1 |
k 1 |
k 1 |
называют статическими моментами системы относительно координатных плоскостей:
Очевидно, что
M xc SOyz , M yc SOxz , M zc SOxy .
Если xC , yC , или zC равны нулю, то и соответствующий статический момент равен нулю.
Рассмотрим твёрдое тело . Выделим в нем элементарный элемент массой dm . Пусть r радиусвектор этого элемента, его коорди-
наты x, y,z .
Тогда масса твёрдого тела
M dm .
Радиус-вектор центра масс
Рис. 2.1.2
rc M1 r dm.
Координаты центра масс
x |
1 |
|
x dm , y |
1 |
|
y dm , z |
1 |
|
zdm. |
|
M |
M |
M |
||||||||
C |
C |
C |
|
|||||||
|
|
|
|
|||||||
Скорость и ускорение центра масс твёрдого тела найдутся по формулам:
vC M1 v dm , aC M1 a dm ,
Здесь v и a – скорость и ускорение произвольной точки тела.
Статические моменты твёрдого тела запишутся так:
11
|
|
O r dm M rC – статический момент относительно центра О; |
||
S |
||||
|
|
|
|
|
|
|
|
|
|
SOyz = |
x dm MxC ; |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SOxz = |
|
статические моменты относительно |
||
y dm MyC ; |
|
|||
|
|
|
|
координатных плоскостей. |
SOxy = |
|
|
||
z dm MzC . |
|
|||
|
|
|
|
|
|
|
|
|
|
2.2. МОМЕНТЫ ИНЕРЦИИ
Положение центра масс не может полностью характеризовать распределение масс М.С. и Т.Т., вследствие чего при изучении динамики М.С. вводится характеристика распределения масс – момент инерции данного тела (системы) относительно точки, оси или
плоскости.
|
а . П о л я р н ы й м о м е нт и н е р ц и и |
|
Моментом инерции точки отно- |
|
сительно центра O (полярным мо- |
|
ментом инерции) называют произве- |
|
дение массы точки на квадрат рассто- |
|
яния от точки до центра O : |
Рис. 2.2.1 |
IO m r2 . |
Рассмотрим М.С. Mk |
материальных точек. Пусть mk масса точки |
n |
|
M k , xk , yk ,zk – её координаты. rk , её радиус-вектор.
Моментом инерции М.С. относительно центра (полярным моментом инерции) называется сумма произведений масс точек М.С. на квадраты их расстояний до центра.
n
IO mk rk2 .
k 1
12
б . О с е в о й м о м е нт и н е р ц и и
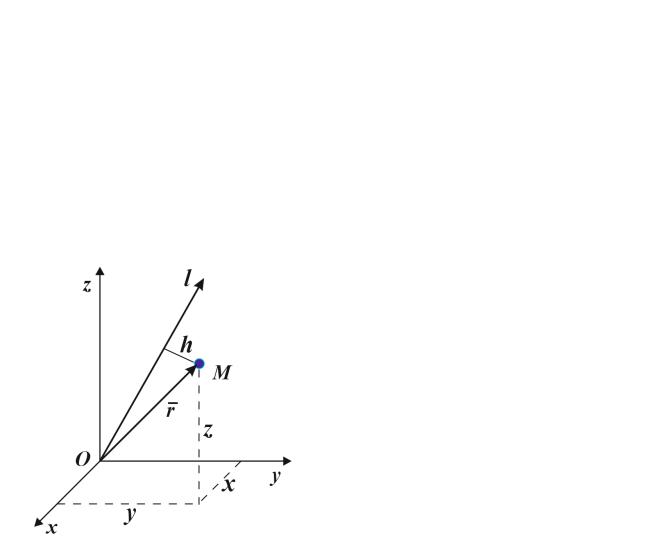
Осевым моментом инерции точки относительно оси l называют произведение массы точки на квадрат расстояния от точки до оси l :
Il m h2 .
Осевые моменты инерции точки относительно осей прямой декартовой системы координат составляют:
Осевым моментом инерции (моментом инерции М.С. относительно оси) называется величина, равная сумме произведений масс частиц М.С. на квадрат их расстояний до оси.
I
I
I
Ix m y2 z2 , |
|
I y m x2 |
|
|
|
z2 , |
|
Iz m x2 |
|
y2 . |
|
|
|
n
x mk yk2 zk2 , k 1
n
y mk xk2 zk2 , k 1
n
z mk xk2 yk2 . k 1
Сложив осевые моменты инерции, получим: |
|
|
|
|
|
|
|
|
||||||||
I |
x |
I |
y |
I |
z |
2 m x2 |
y2 z2 , |
2I |
O |
I |
x |
I |
y |
I |
z |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
Осевой момент инерции часто представляют в виде произведения массы М.С. на квадрат некоторой длины i . Например
Iz M i2
Величина i называется радиусом инерции тела относительно данной оси. Радиус инерции тела равен тому расстоянию оси, на которое нужно поместить точку с массой равной массе тела, чтобы её момент инерции относительно оси был равен моменту инерции всего тела.
Для тел с непрерывным распределением массы осевые моменты инерции
определяются интегралами по массе: |
|
|
|
||
Ix |
y2 z2 dm , I y |
|
x2 z2 dm , Iz |
|
x2 y2 dm . |
M |
|
M |
|
M |
|
13
в . Ц е нт р о б е ж н ы й м о м е н т и н е р ц и и
Центробежные моменты инерции (произведения инерции) учитывают зна-
ки координат. |
|
|
|
Для точки: |
|
|
|
I yx Ixy |
m xy, Ixz |
Izx m xz , I yz Izy |
m yz . |
где I xy , I xz , I yz – центробежные моменты инерции точки относительно |
|||
соответствующих осей. |
|
|
|
Для механической системы |
точек с массами |
mk , координатами |
|
xk , yk ,zk : |
|
|
|
n |
|
n |
n |
Ixy mk xk yk , Ixz mk xk zk , I yz |
mk yk zk . |
||
k 1 |
|
k 1 |
k 1 |
Центробежным моментом инерции М.С. относительно какой-либо пары координатных осей называют сумму произведений масс точек М.С. на произведение их координат по этим осям
Центробежные моменты инерции могут быть положительными, отрицательными и равными нулю, тогда как осевые и полярные моменты только положительны.
Для однородных твёрдых тел моменты инерции определяются по следующим формулам
Ixy x y dm , |
Ixz x z dm , |
I yz y z dm . |
M |
M |
M |
Размерность момента инерции I кг м2 . |
|
|
Г л а в н ы е и ц е нт р а л ь н ы е о с и и н е р ц и и
Ось координат являются центральной осью инерции М.С., если она проходит через центр масс тела. Ось декартовых координат является главной осью инерции М.С. в данной точке, если оба центробежных момента инерции, содержащие в индексах знак этой же оси равны нулю.
Если Ixz I yz 0 , то z – главная ось инерции.
Если I xy I xz 0 , то x – главная ось инерции.
Если I xy I yz 0 , то y – главная ось инерции.
14
Ось главная и проходящая через |
|
центр масс тела будет являться главной |
|
центральной осью инерции тела. |
|
В ряде случаев можно по форме |
|
тела сразу указать, какие оси являются |
|
главными. |
|
Из всех случаев выделим два: |
|
– ось симметрии тела; |
|
– ось, перпендикулярная плоско- |
|
сти симметрии тела с началом в этой |
|
плоскости. |
|
Ось, перпендикулярная плоскости |
|
симметрии тела и имеющая начало в |
Рис. 2.2.2 |
этой плоскости – главная ось инерции |
|
тела. |
|
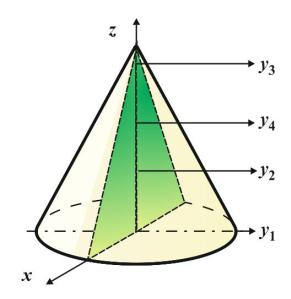
Например, для прямого кругового конуса все изображённые на рисунке |
|
оси – главные оси инерции. |
|
z – ось симметрии тела, x , y1 , y2 , y3 , y4 |
– оси, перпендикулярные плос- |
кости симметрии тела с началом в этой плоскости.
2.3. МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ.
ТЕОРЕМА ГЮЙГЕНСА-ШТЕЙНЕРА
Теорема. Момент инерции тела Iz1 относительно некоторой оси z ра-
вен сумме момента инерции IzC тела относительно оси zC , проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями:
Iz1 IzC Md 2
где М – масса тела, d – расстояние между двумя параллельными осями. Осевые моменты инерции
IzC |
h2dm , |
Iz1 |
h12dm . |
|
M |
|
M |
15
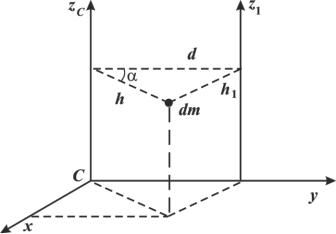
По теореме косинусов найдем
h2 |
h2 |
d 2 2h d cos , |
|
1 |
|
|
|
|
hcos y , |
|
|
где у – координата элемента, тогда |
h2 h2 d 2 |
2 y d . |
|
|
|
1 |
|
Рис. 2.3.1
Подставим полученное выражение в формулу, определяющую момент
инерции Iz1 . |
|
|
|
|
|
|
|
|
Iz1 h2 d 2 |
2 y d dm |
|
h2dm d 2 |
dm 2d |
ydm . |
|||
M |
|
|
|
|
M |
M |
M |
|
Первый интеграл равен IzC |
по определению, второй – массе тела М, а |
|||||||
третий – нулю, так как: |
|
y dm yC 0 , поскольку начало координат совпа- |
||||||
|
M |
|
|
|
|
|
|
|
дает с центром масс. |
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
I |
z1 |
I |
zC |
Md 2 . |
|
|
|
|
|
|
|
|
|
||
2.4. ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ ТЕЛ ПРОСТЕЙШЕЙ ФОРМЫ
Однородное тонкое кольцо массой M , радиусом R
16

Выделим частицу массой dm , расстояние от частицы до центральной оси z равно радиусу. Осевой момент инерции кольца относительно оси z :
|
z |
|
|
|
|
|
Iz |
R2dm R2 dm M R2 . |
|||||
|
|
R |
|
|
|
|
|
|
|
|
M |
M |
|
|
C |
y |
|
|
|
|
|
|
|||||
|
|
|
|
|
Моменты инерции относительно цен- |
||||||||
|
|
|
|
|
|
||||||||
|
|
dm |
|
|
|
тра С кольца и оси z равны между собой: |
|||||||
x |
|
|
|
|
|
|
|
|
|
|
x2 y2 dm M R2 . |
||
|
|
|
|
|
|
|
|
Iz Ic |
|||||
|
Рис. 3.11 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
M |
|
||||
|
Рис. 2.4.1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Но известно, что |
||||
|
|
|
|
|
2Ic I x I y I z . |
|
|||||||
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
I x I y Ic I z . |
|
||||||
В силу симметричности тела |
|
|
|
|
|
|
|
||||||
|
|
|
|
I |
x |
I |
y |
|
I z |
|
M R2 |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Однородный тонкий диск массой M , радиусом R
Выделим в теле диска однородное тонкое кольцо текущим радиусом r , толщиной dr .
Масса элементарного кольца
dm |
M |
2 r dr |
2M r |
dr . |
|
|
|
|
R2 |
|
|
|
|
||||
|
|
R2 |
|
|
|
|
|
|
Осевой момент инерции элементар- |
|
|
Рис. 2.4.2 |
|||||
|
|
|
||||||
ного кольца относительно оси z |
|
|
|
|
|
|||
|
|
|
dI |
|
dm r2 |
|
2M |
r3dr . |
|
|
|
z |
|
||||
|
|
|
|
|
|
R2 |
||
|
|
|
|
|
|
|
||
Осевой момент инерции всего диска относительно оси z после интегрирования по r
17
I |
|
|
2M |
R r3dr |
MR2 |
. |
z |
|
|
||||
|
|
R2 |
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
Так же, как и для тонкого кольца будем иметь:
|
Iz Ic |
|
MR2 |
, 2Ic Ix I y Iz , |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix I y Ic |
|
|
MR2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
I |
x |
I |
y |
|
Iz |
|
|
MR2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
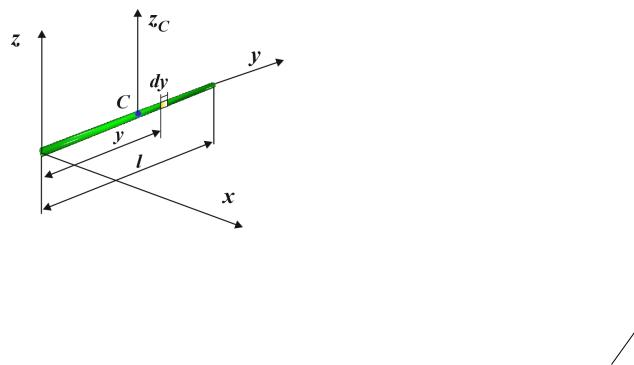
Тонкий стержень массой M , длиной l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Выделим |
частицу |
стержня |
длиной |
|||||||||||||
|
|
|
|
|
|
|
|
dy . Масса частицы |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dm |
M |
dy . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Осевые моменты инерции отно- |
||||||||||||||
|
|
|
|
|
|
|
|
сительно осей z и x равны: |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
y |
|
|
|
|
M l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
I z I x |
|
y2dy |
|
|
. |
(2.3.1) |
|||||||||||
|
|
|
|
|
|
|
|
|
l |
|
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||
Рис. 2.4.3 |
|
|
|
|
|
|
|
|
|
Подсчитаем |
моменты |
инерции |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
стержня относительно центральных осей zc , xc . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Считая, что стержень состоит из двух половинок массой |
|
M |
, длиной l |
, |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||
моменты инерции которых относительно этих осей можно считать по формуле (3.1), получим:
I zc I xc 2 |
M l |
2 |
1 |
|
M l |
2 |
|
|||
|
|
|
|
|
|
|
|
. |
||
2 |
|
3 |
12 |
|
||||||
|
2 |
|
|
|
|
|||||
18
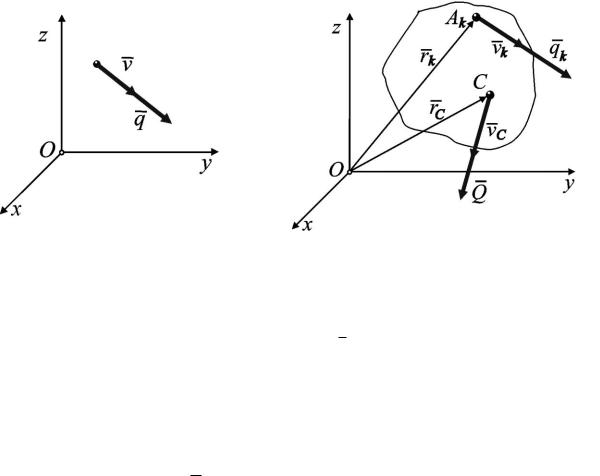
3.Общие теоремы динамики
3.1.КОЛИЧЕСТВО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
Количество движения есть первая, векторная мера механического движения. Для материальной точки массы m , движущейся в пространстве Oxyz со скоростью v , количество движения точки есть вектор, равный произведению массы точки на её скорость (рис. 3.1.1):
q m v .
Проекции количества движения на координатные оси соответственно равны:
qx m vx m x, qy m v y m y, qz m vz m z.
Р
Рис. 3.1.1 Рис. 3.1.1
Рассмотрим движение механической системы Ak n материальных точек в пространстве Oxyz .
Пусть точка Ak , радиус-вектор которой rk и масса mk , движется со ско-
ростью vk . Количество движения этой точки qk mvk (рис. 3.1.2).
Количеством движения механической системы называют сумму количеств движений точек системы:
n
Q qk
k 1
n
mk vk .
k 1
19
