3.1. Решение нелинейных уравнений

Если нелинейное уравнение достаточно сложное, то отыскание его корней ­­– процесс нетривиальный. Рассмотрим, какими средствами обладает Scilab для решения этой задачи. В общем случае аналитическое решение уравнения f(x)=0 можно найти только для узкого класса функций. Чаще всего приходится решать это уравнение численными методами.

Численное решение уравнения проводят в два этапа:

1. отделяют корни уравнения (находят достаточно тесные промежутки, в которых содержится только один корень; эти промежутки называют интервалами изоляции корня, определить их можно, изобразив график функции или любым другим методом, основанным на том, что непрерывная функции f(x) имеет на интервале [a,b] хотя бы один корень, если она поменяла знак f(a)∙f(b)<0, a и b называют пределами интервала изоляции;)

2. на втором этапе проводят уточнение отделенных корней (находят корни с заданной точностью).

В Scilab существует функция fsolve(x0,f), которую так же можно применить для решения алгебраических уравнений. Подробно эта функция будет описана далее, так как ее можно использовать для решения нелинейных уравнений, отличных от алгебраических, и для решения систем линейных и нелинейных уравнений.

Пример 3.1.

Найти решение уравнения y(x)=0, если y(x)=x5–x3+1.

Решим эту задачу при помощи функции fsolve(x0,f), где x0 – начальное приближение, f– функция, описывающая левую часть уравнения y(x)=0. Введем и выполним следующую недлинную программу:

-->deff('[f]=y(x)','f=x^5-x^3+1')

-->X=fsolve(-2,y)

X =

- 1.2365057

Рассмотрим листинг программы, который содержит ход решения задачи.

В первой строке происходит определение функции y(x) в виде исходного полинома.

Во второй строке вызывается команда fsolve(-2,y), для отыскания корней функции y. В качестве начального приближения задано число –2, так как не трудно видеть, что полином имеет единственный действительный корень в интервале от –2 до –1.

Пример 3.2. Рассмотрим пример поиска корня следующего нелинейного уравнения с помощью программы SciLab:

.

Этап 1. Построим график для определения примерного значения корня (рис. 3.1).

Программа

x=0:0.1:1; // график служит для определения примерной

f=0.05-sin(x).^2; // величины корня

plot(x,f)

xgrid()

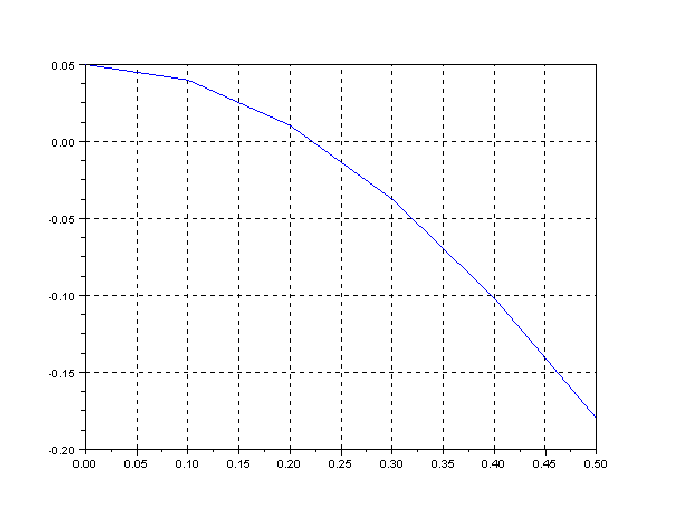
Рис. 3.1. Результат выполнения программы в виде графика

Этап 2. Рассчитаем уточнённое значение корня.

Продолжение программы

deff('[F]=f(x)','F=0.05-sin(x).^2') // программа в

x=fsolve(0,f) // окне редактора

Результат

x = // результат расчета в

0.2255134 // командном окне

3.2. Вычисление определенного интеграла

Вычислить определенный интеграл можно с помощью SciLab разными способами.

Способ 1. С помощью команды intsplin. Это интегрирование экспериментальных данных с помощью сплайн-интерполяции. Известно значение интегрируемой точки в дискретных точках (узлах). Синтаксис команды v = intsplin([x,] s)

Здесь параметры x : вектор x координат данных, упорядоченных по возрастанию. Значение по умолчанию 1:size(y,'*') s : вектор y координат данных. v : значение интеграла Вычисляется численное значение определенного интеграла от функции f(x) в пределах от x0 от x1. 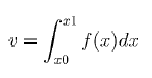При вычислении функцияf описывается экспериментальными значениями так, что s(i)=f(x(i)) и x0=x(1), x1=x(n). Между узловыми точками функция интерполируется с использованием сплайна. Пример 3.3. Произведём численное интегрирование дискретно заданной функции y(x)=x² в интервале [1,6]. Аналитически вычисленное значение его =6³/3-1/3=71.666667 .

Программа: x=[1.,2.,3.,4.,5.,6.]; y=[1,4,9,16,25,36]; v=intsplin(x,y)

Результат: v = 71.666667 Способ 2. С помощью команды inttrap. Интегрирование экспериментальных данных с помощью трапецеидальной интерполяции (метод трапеций).

Синтаксис команды v = inttrap([x,] s)

Параметры x : вектор координат x, упорядоченный по возрастанию. По умолчанию принимает значение 1:size(y,'*') s : вектор y координат данных (значения интегрируемой функции). si=f(xi) v : значение интеграла

Вычисляется 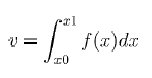где функция f описана набором экспериментальных значений в узлах: s(i)=f(x(i)) и x0=x(1), x1=x(n) При вычислении интеграла между соседними узлами функция интерполируется линейно. Этот метод вычислений называется методом трапеций. Пример 3.4.

Программа для вычисления интеграла методом трапеций.

t=0:0.1:%pi; inttrap(t,sin(t)) Результат: ans = 1.9974689 Способ 3. С помощью команды integrate. Это интегрирование по квадратуре. Может задаваться требуемая точность вычислений.

Синтаксис [x]=integrate(expr,v,x0,x1 [,ea [,er]])

Параметры expr : внешний объект Scilab v : строка (переменная интегрирования) x0, x1 : действительные числа (пределы интегрирования) ea, er : действительные числа (предельная абсолютная ошибка). По умолчанию принимает значение 0. er : действительное число, (предельная относительная ошибка). По умолчанию принимает значение 1.d-8. Вычисляется 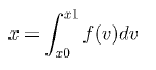Функцияf задана в виде аналитической зависимости от v. Оценка надежности вычисления удовлетворяет следующему требованию точности: abs(I-x)<= max(ea,er*abs(I)), где I означает истинное значение интеграла. Пример 3.5. integrate('sin(x)','x',0,%pi) integrate(['if x==0 then 1,'; 'else sin(x)/x,end'],'x',0,%pi) Способ 4. С помощью команды intg. Интегрируемая функция задана извне: либо в виде набора дискретных точек, либо вычисляется с помощью внешней подпрограммы. Может задаваться требуемая точность вычислений.

Синтаксис команды [v,err]=intg(a,b,f [,ea [,er])

Параметры a, b : действительные числа f : внешняя (функция или список строк) ea, er : действительные числа ea : требуемая абсолютная ошибка точности вычисления. По умолчанию принимает значение 0. er : относительная ошибка точности вычисления. Принимает значение по умолчанию 1.d-8 err : оценка абсолютной ошибки результата. Вычисляется определенный интеграл от a до b от f(t)dt. Оценка точности вычислений: abs(I-v)<= max(ea,er*abs(I)), где I - точное значение интеграла. Функция f может быть: 1) задана в дискретных узловых точках 2) именем внешней процедурой, написанной на языке, например, fortran. 3) записанной в виде строки как list(f,x1,x2,...) Метод вычислений в описании не указан.

Пример 3.6. Вычисление интеграла .

Программа

deff('[F]=f(x)','F=x.^3+cos(x)') // программа в

J=intg(0,1,f) // окне редактора

Результат

J = // результат расчета в

1.091471 // командном окне

Задания по выполнению лабораторной работы

Задание 1. Вычислить значения функции и построить график зависимостиот. Аргументизменяется от 0 до 1 с шагом

1.1

1.2

1.3

Задание 2. Найти корни полинома.

2.1.

2.2.

2.3.

Задание 3. Решить нелинейное уравнение

3.1.

3.2.

Задание 4. Вычислить определенный интеграл

4.1.

4.2.

4.3.

Приложение. Примеры графиков

График функции

Литература

1. Е.Р. Алексеев, О.В. Чеснокова, Е.А. Рудченко. Scilab: Решение инженерных задач. – М.: ALT Linux; БИНОМ. Лаборатория знаний, 2008

2. М.И. Павлова. Руководство по работе с пакетом Scilab.

http://www.csa/ru/~zebra/my-scilab/index/html

3. И.С. Тропин, О.И. Михайлова, А.В. Михайлов. Численные и технические расчеты в среде Scilab. Учебное пособие. – Москва: 2008, 65стр. (для школьников, Linux)

http://www.unux/ru/static/MethodBooks-Scilab/Scilab/pdf

4. Е.Р. Алексеев. Scilab – теория и практика на русском языке.

http://teacher.dn-ua.com/Math/Scilab/Scilab.html

Содержание

Введение………………………………………………………………….. 3

1.Scilab-5.1.1. Работа в диалоговом режиме…………………………… 4

1.1. Командное окно…………………………………………………. 4

1.2. Вектора и матрицы……………………………………………… 7

1.3. Построение графиков на плоскости……………………………

1.4. Вывод нескольких графиков в одном окне…………………….

1.5. Построение трехмерных графиков……………………………… 1.6. Решение некоторых задач линейной алгебры в диалоговом режиме……………………..

1.6.1. Вычисление определителя…………………………………..

1.6.2. Линейные алгебраические уравнения………………………

1.6.3. Определение корней полинома……………………………

2. Разработка программы в Scilab………………………………………

2.1. Использование редактора SciPad…………………………………