Лекция 14. Непрерывность функции
.docЛекция 14. Непрерывность функции.
14.1. Определения непрерывности функции.
Определение 14.1.
Функция
![]() называется непрерывной
в точке
a,
если она удовлетворяет следующим трём
условиям:
называется непрерывной
в точке
a,
если она удовлетворяет следующим трём
условиям:
1)
![]() определена в точке а (то есть существует
определена в точке а (то есть существует
![]() );
);
2)
![]() имеет конечный предел функции при
имеет конечный предел функции при
![]() ;
;
3) этот предел
равен частному значению функции в точке
а, то есть
![]() .
.
Определение 14.2.
Функция
![]() называется непрерывной
справа (слева) в точке
a,
если правое (левое) предельное значение
этой функции в точке a
существует и равно частному значению
называется непрерывной
справа (слева) в точке
a,
если правое (левое) предельное значение
этой функции в точке a
существует и равно частному значению
![]()
![]() .
.
Пример 14.1.
Приведём примеры непрерывных функций:
1)
![]() ,
так как
,
так как
![]() .
.
2)
![]() при
при
![]() .
.
3) Функция
![]() свойством непрерывности в точке
свойством непрерывности в точке
![]() не обладает.
не обладает.
Определение непрерывности в точке а может быть записано и так:
![]() ,
,
то есть для непрерывной функции возможна перестановка символов предела и функции. Очевидно, что непрерывность функции в данной точке выражается непрерывностью её графика при прохождении данной точки (без отрыва карандаша от листа бумаги).
|
Дадим аргументу
а
приращение
Рис. 14.1. |
|
Определение 14.3.
Функция
![]() называется непрерывной
в точке
а, если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции:
называется непрерывной
в точке
а, если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции:
![]() .
.
Определение 14.4. Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва функции.
Например, функция
Дирихле разрывна в каждой точке
![]() .
.
Точки разрыва имеют различный характер и классифицируются следующим образом.
1) Если
![]() ,
то а
называется точкой
устранимого разрыва функции
,
то а
называется точкой
устранимого разрыва функции
![]() .
При этом значение
.
При этом значение
![]() может быть и не определено.
может быть и не определено.
2) Если
![]() ,
то а
называется точкой
разрыва с конечным скачком функции
,
то а
называется точкой
разрыва с конечным скачком функции
![]() .
Значение
.
Значение
![]() может быть любым, а может быть и не
определено.
может быть любым, а может быть и не
определено.
3) Конечный скачок
и устранимый разрыв функции
![]() называются разрывами
I рода.
Их отличительным признаком является
существование конечных односторонних
пределов
называются разрывами
I рода.
Их отличительным признаком является
существование конечных односторонних
пределов
![]() и
и
![]() .
.
Все другие разрывы называются разрывами II рода. В точке разрыва II рода хотя бы один из односторонних пределов равен бесконечности или не существует.
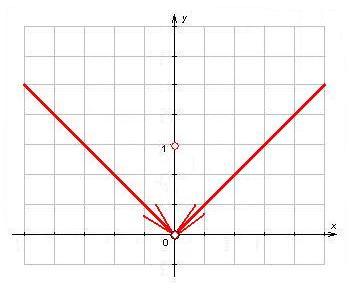
Пример 14.2.
1) Пусть
 Очевидно,
Очевидно,
![]() ,
но
,
но
![]() (рис. 14.2). Следовательно,
(рис. 14.2). Следовательно,
![]() – точка устранимого разрыва функции
– точка устранимого разрыва функции
![]() .
Если положить
.
Если положить
![]() ,
то разрыв устраняется.
,
то разрыв устраняется.
|
|
Рис. 14.2. |
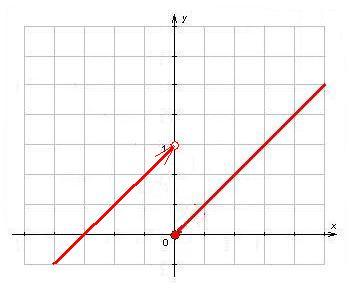
2) Пусть
 Здесь
Здесь
![]() ,
,
![]() (рис. 14.3). Следовательно,
(рис. 14.3). Следовательно,
![]() – точка разрыва с конечным скачком
функции
– точка разрыва с конечным скачком
функции
![]() .
При переходе через точку
.
При переходе через точку
![]() значения функции
значения функции
![]() меняются скачком от значений, сколь
угодно близких к 1 при
меняются скачком от значений, сколь
угодно близких к 1 при
![]() к значению, равному 0 в точке
к значению, равному 0 в точке
![]() ,
и значениям, сколь угодно близким к 0
при
,
и значениям, сколь угодно близким к 0
при
![]() .
.
|
|
Рис. 14.3. |
3) Пусть
![]()
![]() .
Определим односторонние пределы:
.
Определим односторонние пределы:
![]() ,
,
![]() .
Точка
.
Точка
![]() – точка разрыва функции
– точка разрыва функции
![]() II
рода (рис. 14.4).
II
рода (рис. 14.4).
|
|
Рис. 14.4. |
Определение 14.5.
Функция
непрерывна
на множестве
![]() ,
если она непрерывна в любой точке
,
если она непрерывна в любой точке
![]() .
Функция непрерывна
на интервале
.
Функция непрерывна
на интервале
![]() или на
сегменте
или на
сегменте
![]() ,
если
,
если
![]() ;
;
![]() .
.
14.2. Свойства функций, непрерывных в точке.
♦ Теорема 14.1.
1) Если
функции
![]() и
и
![]() определены на
определены на
![]() и непрерывны в точке a,
то их алгебраическая сумма (разность)
и непрерывны в точке a,
то их алгебраическая сумма (разность)
![]() ,
произведение
,
произведение
![]() и частное
и частное
![]()
![]() являются функциями, непрерывными в
точке a.
являются функциями, непрерывными в
точке a.
Доказательство следует из определения непрерывности функции и аналогичных свойств пределов функций. ■
♦ 2) Если функция
![]() непрерывна в точке а и
непрерывна в точке а и
![]() ,
то существует такая окрестность точки
а, в которой
,
то существует такая окрестность точки
а, в которой
![]() .
.
Доказательство
этого свойства основывается на том, что
при малых приращениях аргумента
![]() в соответствии с определением 14.3 можно
получить как угодно малое приращение
функции
в соответствии с определением 14.3 можно
получить как угодно малое приращение
функции
![]() ,
так что знак функции
,
так что знак функции
![]() в окрестности точки а
не изменится. ■
в окрестности точки а
не изменится. ■
♦ 3) Если функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
а функция
,
а функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
и
,
и
![]() ,
то сложная функция
,
то сложная функция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
Доказательство.
Малому приращению аргумента
![]() в силу определения 14.3 соответствует
как угодно малое приращение
в силу определения 14.3 соответствует
как угодно малое приращение
![]() ,
приводящее, в свою очередь, в силу того
же определения непрерывности функции
,
приводящее, в свою очередь, в силу того
же определения непрерывности функции
![]() к как угодно малому приращению
к как угодно малому приращению
![]() ■
■
Свойство 3 может быть записано в виде
![]() ,
,
то есть под знаком сложной функции можно переходить к пределу.
Функция
![]() называется непрерывной
на промежутке
Х,
если она непрерывна в каждой точке этого
промежутка. Можно доказать, что все
элементарные функции непрерывны в
области их определения.
называется непрерывной
на промежутке
Х,
если она непрерывна в каждой точке этого
промежутка. Можно доказать, что все
элементарные функции непрерывны в
области их определения.
Пример 14.3.
Доказать
непрерывность функции
![]() .
.
Найдём
![]() .
Таким образом, получили, что
.
Таким образом, получили, что
![]() ,
следовательно, по определению 14.3 функция
,
следовательно, по определению 14.3 функция
![]() является непрерывной на всей числовой
оси.
является непрерывной на всей числовой
оси.
Отметим ещё некоторые свойства функций, непрерывных на отрезке:
|
1) Если функция
|
|
|
|
Рис. 14.5. |
|
|
|
|
2) Если функция
|
|
|
|
Рис. 14.6. |
|
|
|
|
3) Если функция
|
|
|
|
Рис. 14.7. |