6. Базис на плоскости и в пространстве.

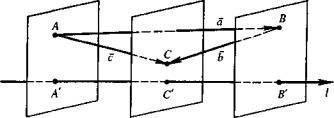
Определение. Базисом на плоскостиназываются два любых линейно независимых вектора.

Из теоремы 2 (см. п. 4) следует, что два любых неколлинеарных вектора образуют базис. Пусть любой вектор на плоскости, а векторыиобразуют базис. Так как на плоскости всякие три вектора линейно зависимы, то векторлинейно выражается через векторы базиса, т. е. выполняется соотношение

.

Если вектор представлен в виде (3), то говорят, что онразложен по базисуобразованному векторамии. Числаиназываюткоординатами вектора на плоскости относительно базисаи

1 . Разложение вектора поиявляется единственным

Доказательство. Допустим, что наряду с разложением (3) имеет место разложение

Покажем, что в этом случае Действительно, вычитая равенство (4) из равенства (3), получаем соотношение

(Возможность почленного вычитания равенств (4) и (3) и производимой группировки членов вытекает из свойств линейных операций над векторами (см. п. 2).) Так как векторы базиса ,линейно независимы, тои. Отсюда, т.е. разложение векторапо базису,единственно.

Определение. Базисом в пространственазываются три любых линейно независимых вектора.

Из теоремы 2 (см. п. 5) следует, что три любых некомпланарных вектора образуют базис. Как и в случае плоскости, устанавливается, что любой вектор разлагается по векторам,и

причем это разложение единственное.

Числа ,,называюткоординатами векторав пространстве относительно базиса,и.

Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными операциями над числами - координатами этих векторов.

Теорема . При сложении двух_векторов иих координаты (относительно любого базисаиили любого базиса,и) складываются. При умножении векторана любое число, а все его координаты умножаются на это число.

Доказательство. Пусть, например,

.

Тогда в силу свойств линейных операций (см. п. 2)

В силу единственности разложения по базису ,,теорема для этого базиса доказана.

7. Проекция вектора на ось и ее свойства.

Определение 1. Углом между векторамииназывается наименьший угол, на который надо повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.

называется направленная прямая. Направление прямой на рисунке обычно обозначается стрелкой. Заданное направление оси считается положительным, противоположное - отрицательным.

Рассмотрим ось l, положительное направление которой совпадает с направлением единичного вектора, расположенного на осиl. Такой вектор называетсяортом оси l.

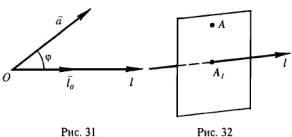
Определение 2. Углом между вектором и осью  lназывается уголмежду векторамии(рис. 31).

Определение 3. Проекцией точки А на ось l (рис. 32) называется точкав которой пересекается ось с плоскостью, перпендикулярной кl , проходящей через точкуА.

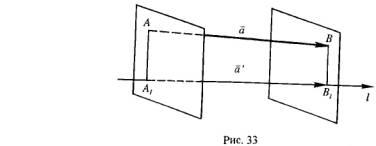
Определение 4 Компонентой (составляющей) вектора = на ось (рис. 33) называется вектор, где,соответственно проекции точекА, В на  l .

Определение5. Проекцией вектора на осьl() называется длина его компонентына ось l, взятая со знаком «плюс», если направление компоненты совпадает с направлением осиl , и со знаком «минус», если направление компоненты противоположно направлению оси .

Если = ,то полагают =.

Теорема I  Проекция вектора на ось l равна произведению его модуля на косинус угламежду этим вектором и осью  l.

= .

Доказательство. Так как вектор =свободный, то можно предположить, что начало его О лежит на оси l(рис. 34).

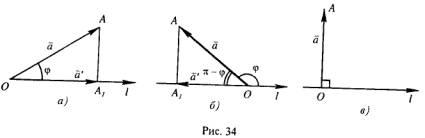
Если угол острый , то направление компоненты=, векторасовпадает с направлением осиl  (рис 34,а).

В этом случае имеем  = += .Если же угол (рис. 34, б), то направление компоненты=векторапротивоположно направлению осиl.Тогда получаем==cos(-) =сos

Наконец, если =(рис. 34, в), то= 0 и соs= 0. Таким образом, снова имеем соотношение =соs.

Следствие1 Проекция вектора на ось положительна, если вектор образует с осью острый угол, отрицательна, если этот угол тупой, равна нулю, если этот угол прямой.

Следствие 2. Проекции равных векторов на одну и ту же ось равны между собой.

Теорема 2. Проекции векторов ,на данную ось обладают следующими свойствами:

Доказательство. Свойство (5) иллюстрирует рис. 35. Докажем свойство (6). Считая, что угол между вектором  =и направлениемl равен, имеем при> О= ||соs=||соs=

при  < 0= ||соs(-) = -||соs ( -) =||соs=(при  < 0 вектор направлен в сторону, противоположную направлению ; если образует с l  угол , то образует с l угол -). При  = 0 левая и правая части (6) обращаются в нуль.