
- •Элементарные правила раскрытия неопределенностей при вычислении пределов.
- •Первый замечательный предел.
- •Второй замечательный предел.
- •Производная функции. Задача Ньютона.
- •Механический, геометрический смысл производной функции.
- •Асимптоты кривой.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Первообразная и неопределенный интеграл и его свойства.
- •Простейшие приемы интегрирования.
- •Частное и общее решение. Частный и общий интеграл. Задачи Коши.
- •Дифференциальное уравнение с разделенными переменными и его решение.
- •Дифференциальное уравнение с разделяющимися переменными и его решение.
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами.
- •Элементы комбинаторики: размещения, перестановки, сочетания, свойство сочетаний.
- •Виды событий. Примеры.
- •Классическое определение вероятностей. Свойства вероятности.
- •Статистическое определение вероятностей.
- •Геометрическое определение вероятностей.
Функция. Способы задания функции. Область определения и область изменения функции.Функция – это соответствие между двумя множествами Х и У, при котором каждому элементу множества Х найдется единственный элемент множества У. Способы задания функции:
Табличный (значения функции задаются в виде табличных значений).
Графический (значения функции задаются в виде графиков).
Аналитический (с помощью формулы).
Описательный способ (свойства функции задаются словесно).Область определения функции – это множество значений переменной Х, при которых функция принимает действительные значения (обозначается D(f)).
Область изменения функции – это множество значений, которые принимает сама функция (обозначается E(f)).
Предел функции. Теоремы о пределах. Односторонние пределы функции.
Предел функции в заданной точке - это такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
lim f(x) = a
1 Теорема:
Предел суммы есть сумма пределов.
lim (f(x) + u(x)) = lim f(x) + lim u(x)
2 Теорема:
Предел произведения есть произведение пределов.
lim f(x)*u(x) = lim f(x) * lim u(x)
3 Теорема:
Предел частного есть частное пределов (если знаменатель не обращается в 0).
4 Теорема:
Предел функции равен функции в предельной точке аргумента.
lim f(x) = f (limx)
Односторонние пределы функции:
Это предел числовой функции , подразумевающий "приближения" к предельной точке с одной стороны. Чтобы функция имела предел необходимо существование односторонних пределов, они должны быть равны и конечны.
Непрерывность функции в точке. Классификация разрывов функции.
Функция непрерывна, если предел функции и ее значение в этой точке равны.
lim f(x) = f (x0) при х->x0
Функция непрерывна в точке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
lim (дельта)y = 0
(дельта)y = y*(x0+(дельта)x) – y(x0) – приращение функции
(дельта)х – приращение аргумента
Функция непрерывна в точке, если существуют конечные односторонние пределы функции и они равны между собой, и равны значению функции в этой точке.
f (x0-0) = f (x0+0) = f (x0) < бесконечность - условия непрерывности функции в точке
Классификация разрывов функции:
Точка разрыва функции – это точка Х0, в которой нарушаются условия непрерывности функции (3).
I род, неустранимый.
Точка Х0 называется точкой неустранимого разрыва I рода, если существуют односторонние пределы функции, они конечны, но не равным между собой.
f (x0-0) НЕ равно f (x0+0) < бесконечность
б = | f (x0-0) – f (x0+0) | - скачок
1род,
неу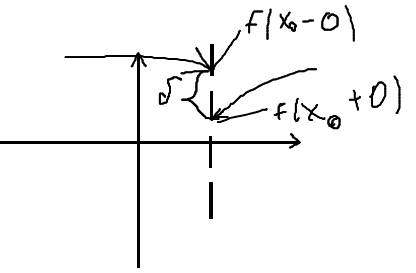 2род.
2род.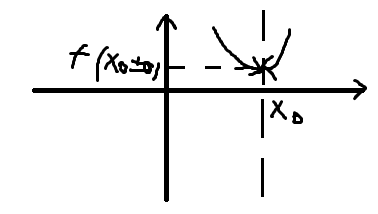
II род, устранимый.
Точка Х0 называется точкой устранимого разрыва I рода, если существуют конечные, односторонние пределы функции, они равны между собой, но не равны значения функции в этой точке.
f (x0-0) = f (x0+0) НЕ равно f (x0)
Замечание: устранимый разрыв 1 рода можно искусственно устранить. Для этого надо значение функции f(X0) прировнять к значению.
f (x0) = f (x0+0)
II род.
Точка X0 называется точкой разрыва II рода, если хотя бы 1 из односторонних пределов функции или оба не существуют или равны бесконечности.
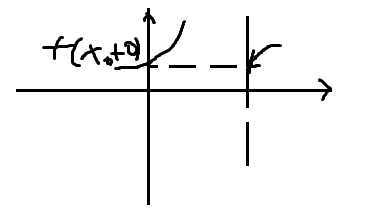
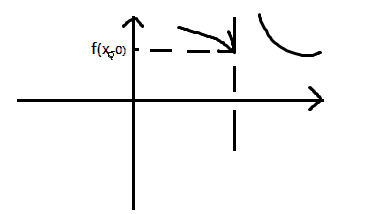
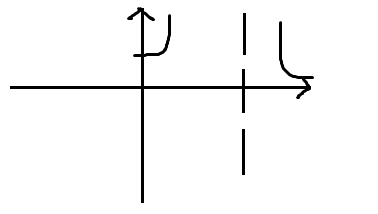
f (x0-0) = бесконечность f (x0+0) = бесконечность f (x0+0) = бесконечность
Элементарные правила раскрытия неопределенностей при вычислении пределов.
Правила:
Использование замечательных пределов;
Применение правила Лопиталя;
Производные и дифференциалы высших порядков.
Первый замечательный предел.
lim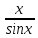 = (0\0) = 1 x->0
= (0\0) = 1 x->0
lim = (0\0) = 1 x->0
= (0\0) = 1 x->0
Второй замечательный предел.
lim
(1+X)^ = (1∞)
= e x->0
= (1∞)
= e x->0
lim
(1+
 )x
= (1∞)
= e x->∞
)x
= (1∞)
= e x->∞
Производная функции. Задача Ньютона.
Производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю произвольным образом.
y|
=
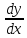 = lim
= lim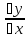 = lim
= lim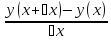 ⧍x->0
⧍x->0
Задача Ньютона:
Найти скорость неравномерного прямолинейного движения точки в каждый момент времени t.
Решение:
t+⧍t => S(t) + ⧍S = S (t+⧍t)
⧍S = S (t+⧍t) – S(t) - приращение функции
Найдем среднюю скорость движения точки, считая, что за небольшой промежуток времени точно двигалась равномерно
Vср=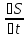
Найдем мгновенную скорость движения точки.
Vмгн
= lim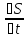 = lim
= lim
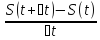 = S|
(t) =
= S|
(t) =
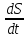 = S (t)⧍t->0
= S (t)⧍t->0
Механический, геометрический смысл производной функции.
Механический смысл:
Скорость неравномерного прямолинейного движения точки равна производной пути по времени.
v(t)
=
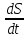 = S|
(t)
= S|
(t)
Ускорение неравномерного движения точки равно:
a
=
 = S||
(t)
= S||
(t)
Сила переменного тока равна производной количества по времени.
I
(t)
=
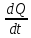 = Q|
(t)
= Q|
(t)
Геометрический смысл производной
y|
=
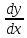 = lim
= lim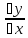 = lim
= lim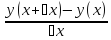 ⧍x->0
⧍x->0
Уравнения касательной и нормали.
Уравнение нормали:
y-y0 = (1\y| (x0)) *(x-x0)
Уравнение касательной:
y-y0 = y|(x0)(x-x0)
Правила и формулы дифференцирования.
Постоянное число можно (и нужно) вынести за знак производной.
Производная суммы равна сумме производных.
Производная произведения функций.
Производная частного функций.
Производная сложной функции.
(u(v))| = u|(v)*v|
Сначала находим производную внешней функции u|(v)
Производная неявно заданной функции.
F (x;y) = 0
yx| - ?
Продифференцируем каждое слагаемое уравнения, считая, что производная
x|=1; y|=y|
Из полученного выражения найдем y|.
x2 - y3 = Sin (x-y)
2x – 3y2*y| = Cos (x-y)(1-y|)
2x – 3y2*y| = Cos (x-y) – Cos (x-y)*y|
Cos (x-y)*y| - 3y2*y| = Cos (x-y) – 2x
y|*(Cos (x-y) – 3y2) = Cos (x-y) – 2x
y|
=
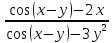
Первая, вторая производные параметрически заданной функции.
yx’ = yt’ \ xt’
yxx” = (yx’)t’ \ xt’
Дифференциал функции и его вычисление.
Дифференциал – это главная часть приращения функции. Линейная относительно ⧍Х и обозначается dy.
dy = y'(x)*⧍x = y’(x)*dx - рабочая формула для вычисления дифференциала функции
dx = x'(x)*⧍x = ⧍x
Для того, чтобы найти дифференциал функции, надо производную функции умножить на дифференциал независимой переменной.
Правило Лопиталя.
Если существует отношение 2-ух бесконечно малых или 2-ух бесконечно больших функций, то существует и предел их отношения, и он равен пределу отношений их производных, равен пределу отношения их вторых производных и т.д. (0\0; ∞\∞).
lim
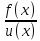 = lim
= lim
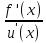 = lim
= lim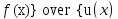
Производные и дифференциалы высших порядков.
Производные: Дифференциалы:
y” = (y’)’ dy = y’(x) dx
y’’’ = (y”)’ dny = y(n)(x) dxn
y(n) = (y(n-1))’
Признаки возрастания и убывания функции. Экстремумы функции.
Функция возрастает, если большему значению аргумента соответствует большее значение функции.
Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I.
Экстремумы функции:
Экстремум – это максимальное или минимальное значение функции на заданном множестве.
Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Изогнутость графика функции. Точки перегиба.
График функции y=f(x) называется выпуклым на интервале, если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале , если он расположен выше любой своей касательной на этом интервале.
Точка перегиба - это точка графика функции, в которой меняется направление выпуклости графика (выпуклый - вогнутый), а вторая производная меняет свой знак.
Обычно находится следующим образом:
1) находим вторую производную
2) приравниваем ее к нулю и решаем уравнение. Полученные корни называются КРИТИЧЕСКИМИ ТОЧКАМИ ВТОРОГО РОДА
3) на оси Ох отмечаем эти точки и определяем знаки второй производной на каждом из полученных интервалов
4) как только при переходе через критическую точку вторая производная поменяла знак-вот Вам и точка перегиба...
