
04_Надежность_Закономерности_распред_отказов
.pdf
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
4.Закономерности распределения отказов.
ВП.1 дано представление о законе распределения случайной величины. Очевидно, что при известном законе распределения случайной величины, саму случайную величину также можно считать известной, т.е. определена связь между всеми возможными значениями случайной величины и вероятностями этих значений. В то же время успешное решение практических задач надежности невозможно без знания функциональной зависимости показателей надежности от времени.
Соответственно типу случайной величины, законы распределения делятся на дискретные и непрерывные. Характер изменения показателей надежности во времени во многом зависит от физических процессов, протекающих в рассматриваемых объектах, иначе, от типов возникающих отказов. Следовательно, для различных объектов и для различных типов отказов одного объекта необходимо выбирать различные законы распределения. В случае сложных систем возможно использование композиций нескольких распределений.
Дискретные законы распределения. К дискретным распределениям относят биномиальное, Пуассона, гипергеометрическое, равномерное и некоторые другие.
Биномиальный закон распределения. Рассмотрим воздействие нагрузки на какой-либо объект [2] в процессе его эксплуатации (рис. 4.1).
Очевидно, что нагрузка будет изменяться со временем, причем ее величина зависит от режима работы, внешних условий эксплуатации, характера взаимодействия с другими объектами, иными словами, характер изменения нагрузки носит случайный характер. Величина Gmax на рис. 4.1 представляет собой макси-
мальную нагрузку, которую может выдержать объект в процессе эксплуатации. В идеальных условиях Gmax всегда несколько больше максимального значения
G t , на самом же деле ее величина может быть несколько меньше расчетной из-
за ошибок проектирования, изготовления и сборки, поэтому наступление отказа объекта вследствие превышения нагрузки будет иметь ненулевую вероятность.
Рис. 4.1. Характер изменения нагрузки G t на объект в процессе эксплуатации.
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
Для рассмотрения биномиального закона распределения необходимо отметить некоторые свойства нагрузки G t :
Нагрузка изменяется непрерывно и вследствие инерционности ее изменение на двух соседних малых интервалах времени ( t1 и t2 на рис. 4.1) будет незначи-
тельно. В то же время, на достаточно удаленных друг от друга участках ( t2 и t3 )
изменение нагрузки может быть значительным. Таким образом, количество превышений нагрузкой значения Gmax не зависит от того, сколько их было на дру-
гих, не перекрывающихся участках. Такое свойство нагрузки называется отсут-
ствием последействия.
Следующим свойством нагрузки является то, что превышения ей значения Gmax и моменты их возникновения носят случайный характер, т.е. число превы-
шений зависит только от величины интервала времени наблюдения и не зависит от положения его на оси времени. Это свойство нагрузки называют стационар-
ностью.
Вследствие непрерывности и плавности изменения нагрузки вероятность попадания на малый промежуток времени t двух и более превышений Gmax пре-
небрежимо мала по сравнению с вероятностью попадания одного превышения. Данное свойство принято называть ординарностью, а поток событий (поток отказов, закон распределения), отвечающий всем трем свойствам, называют про-
стейшим.
Выделим на оси времени интервал « t » и обозначим как « m » количество отказов в этом интервале. Тогда вероятность того, что на отрезке времени « t » произойдет ровно « m » отказов:
Pm t P t m , |
(4.1) |
где случайная величина t - число отказов в интервале « t ».
Далее, разделим отрезок « t » на « n » равных частей: |
|
||
t |
t |
. |
(4.2) |
|
|||
|
n |
|
|
Учитывая свойство ординарности, на малом t пренебрегаем вероятностью возникновения нескольких отказов. Тогда вероятность попадания одного отказа определится как « t », вероятность отсутствия отказа «1 t ». Здесь « » - плотность числа отказов (среднее число отказов) в единицу времени. Согласно свойству стационарности « » не зависит от времени. Так как попадание отказов в неперекрывающиеся отрезки времени, события независимые, имеется возможность рассматривать « n » участков длиной « t », как « n » независимых испытаний, в каждом из которых произошел отказ с вероятностью « t t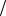 n » и не
n » и не
произошел с вероятностью «1 t 1 t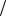 n ». Тогда вероятность события, за-
n ». Тогда вероятность события, за-
ключающаяся в том, что на первых « m » участках длиной « t » отказы произошли, а на оставшихся « n m » не произошли, возможно определить с использованием теоремы об умножении вероятностей:
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
|
t m |
|
|
t n m |
(4.3) |
||
|
n |
|
1 |
n |
. |
||
|
|
|
|
|
|
||
Вероятность того, что на любых « m » участках из « n » произошли отказы, а на остальных – нет, получим с использованием теоремы о сложении вероятностей:
|
|
|
|
|
m |
|
t m |
|
|
t n m |
(4.4) |
|
|
|
|
|
|
Pm,n Cn |
|
|
1 |
|
, |
||
|
|
|
|
|
|
|
n |
|
|
n |
|
|
где |
m |
|
n! |
- число сочетаний из « n |
» по « m », представляющее собой |
|||||||
Cn |
|
|
|
|||||||||
m! n m ! |
||||||||||||
число способов выбора « m » элементов из « n » независимо от того, в каком по-
рядке выбираются элементы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Данное уравнение определяет распределение вероятностей случайного числа |
|||||||||||||||||||
« m », называющееся биномиальным распределением. |
|
|||||||||||||||||||
|
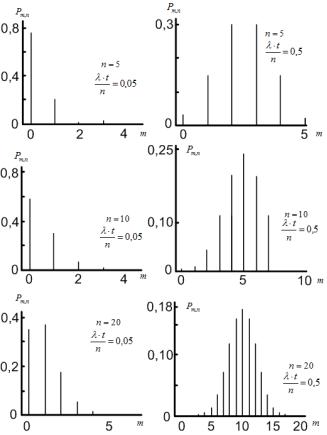
Примерный вид биномиального распределения представлен на рис. 4.2. |
|||||||||||||||||||
|
Следует отметить ряд свойств биномиального распределения: |
|
||||||||||||||||||
|
Максимум Pm, n |
достигается для m , которое определяется неравенством |
||||||||||||||||||
|
|
|
|
|
|
t |
|
n 1 |
1 m |
|
t |
[7]. |
||||||||
|
|
|
|
|
|
|
n |
|
|
n 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При n и |
0 , при постоянном значении t биномиальное распре- |
||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
деление сходится к распределению Пуассона с параметром t . |
Приближение |
|||||||||||||||||||
приемлемо для n 10 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
0,10 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При n биномиальное распределение сходится к нормальному распреде- |
|||||||||||||||||||
лению с |
параметрами |
Tср t , |
|
2 |
|
|
|
|
|
t |
. Сходимость |
хорошая для |
||||||||
|
|
t 1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||
|
t |
|
|
t |
|
|
|
1 |
|
t |
|
|
1 |
|
|
|
|
|
|
|
|
0,5 |
и плохая для |
|
|
|
|
|
, |
|
|
|
|
|
|
, а также вне полосы 3 . |
|||||
|
n 1 |
n 1 |
||||||||||||||||||
|
n |
|
|
n |
|
|
|
n |
|
|
|
|
|
|||||||
Биномиальное распределение является дискретным, его нельзя рассматривать как непрерывную функцию времени. Биномиальное распределение обычно применяется в случаях, когда изделия классифицируются на хорошие и дефектные.
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
Рис. 4.2. Примерный вид и свойства биномиального распределения
Распределение Пуассона. При достаточно большом « n » и ординарности событий, « Pm,n » приближенно равно вероятности:
P |
t lim C |
m |
|
t m |
|
|
t n m |
|
||
|
|
n |
|
1 |
n |
|
||||
m |
n |
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
t |
|
n |
t |
|
|||
|
|
|
|
|
|
|
|
|
t |
. |
(4.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
||
|
n n 1 ... n m 1 |
|
m |
|
|
|
|
|
|
|
|
||||
lim |
|
t |
|
|
|
|
|
|
|
|
|
|
|||
nm |
|
m! |
|
|
|
t m |
|
|
|||||||
n |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
После преобразований получим: |
t m |
|
|
|
Pm t |
e t . |
(4.6) |
||
m! |
||||
|
|
|
Данное выражение представляет собой закон Пуассона с параметром « t », т.е. число отказов « m » в промежутке времени « t » имеет распределение Пуассона с учетом сделанных предположений. Закон Пуассона определяет вероятность появления в малых выборках различных значений случайной величины « m ». На практике часто используется как заменитель биномиального распределения, но имеет и самостоятельное значение: если вероятность появления события в малом промежутке времени « t » пропорциональна « t » и события являются независимыми, то число появлений события в течение данного промежутка времени распределяется по закону Пуассона, называемому также «законом редких яв-

Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
лений». Распределение Пуассона широко используется в теории надежности для описания данных об отказах в первом приближении, таких, например, как число отказов в течение заданного отрезка времени, число дефектов в некоторой большой совокупности и т.д.
Примерный вид закона Пуассона представлен на рис. 4.3. Следует отметить ряд свойств распределения Пуассона:
Pm t максимальна для m t (наибольшее целое число, равное или меньшее
t ).
Для малых значений t распределение сосредоточено вблизи начала координат. С ростом t распределение приобретает ассиметричную колоколообразную форму. Для больших значений ( t 9 ) распределение Пуассона можно приближенно заменить нормальным распределением с параметрами Tср t ,
2 t .
Рис. 4.3. Примерный вид и свойства распределения Пуассона
Непрерывные законы распределения. Экспоненциальный закон распреде-
ления. Допустим, что в рассматриваемом промежутке времени отказов не было, т.е. « m 0 ». Тогда « Pm t » представляет собой вероятность безотказной работы:
Pm 0 t R t e t . |
(4.7) |
|
Плотность распределения в этом случае определится как: |
(4.8) |
|
a t R t e . |
||
|
t |
|
|
|
|
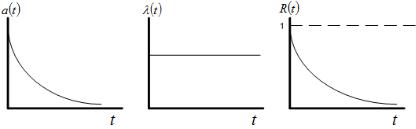
Такое распределение называется экспоненциальным (показательным), т.е. время безотказной работы распределено экспоненциально с параметром « ».
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
Рис. 4.4. Примерный вид экспоненциального распределения. Очевидно, что вероятность отказа:
Q t 1 R t 1 e t , |
(4.9) |
||||||
а интенсивность отказов: |
a t |
|
|
|
|
|
|
t |
|
e t |
const . |
(4.10) |
|||
R t |
e t |
||||||
|
|
|
|
||||
Средняя наработка до отказа определится следующим образом:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Tср R t dt e |
t dt |
|
e t |
|
. |
|
|
(4.11) |
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дисперсия наработки до отказа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
t |
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
DT |
|
2 t |
R t dt Tср |
2 t e |
|
|
|
dt |
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
. |
(4.12) |
||
1 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||||
|
|
t |
|
t |
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
t |
|
e |
|
|
|
|
e |
|
dt |
|
|
|
|
|
Tср |
|
|
|
||||||||
|
|
0 |
|
|
2 |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данный закон распределения является однопараметрическим, т.е. для определения показателей безотказности необходимо знать только значение « ».
Рассмотрим теперь основные свойства экспоненциального закона. Выделим на оси времени промежуток длиной « t t2 t1 » и определим условную вероят-
ность отсутствия отказа в промежутке времени « t » при условии, что он не произошел до момента времени « t1 »:
R t | t1 |
R t |
|
e |
t2 |
e t . |
(4.13) |
|
2 |
|
|
e t1 |
||||
R t1 |
|
||||||
Отсюда следует, что R t | t1 R t , т.е. вероятность отказа в промежутке времени « t » не зависит от выбора момента времени « t1 » и « t2 », а зависит только от длины интервала времени « t2 t1 ». Так как рассматриваемый интервал времени
может находиться на любом этапе эксплуатации объекта, то, согласно экспоненциальному закону распределения технические обслуживания и ремонты не влияют на показатели надежности, а сам объект, является, по сути дела, нестареющим. Тем не менее, этот закон достаточно широко применяется в технике для анализа надежности технических изделий при внезапных отказах, связанных с воздействием случайных факторов, таких как превышение допустимых нагрузок, нарушение правил эксплуатации, снижение допустимых нагрузок из-за ошибок, допущенных при проектировании и изготовлении и т.д.. При этом своевременно проводимые мероприятия по техническому обслуживанию и ремонту восстанавливают работоспособность оборудования по мере его износа и старе-
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
ния, а потому в период нормальной эксплуатации оборудования свойства стационарности, ординарности и отсутствия последействия нарушаться не будут, а поток отказов по-прежнему можно считать простейшим.
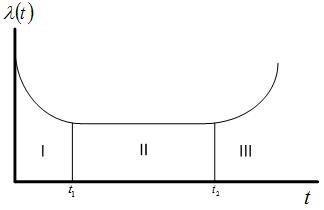
Изменение интенсивности отказов сложного технического изделия можно представить в виде рис. 4.5.
I – период приработки – начальный период эксплуатации, в котором происходит так называемое «выжигание» дефектных элементов. В процессе приработки выявляются наиболее грубые ошибки, допущенные при проектировании, изготовлении и монтаже. Длительность первого периода обычно небольшая, а число отказов может в 1.5 – 2 раза больше, чем в последующие годы эксплуатации.
Рис. 4.5. Примерный вид изменения интенсивности отказов сложного технического изделия в процессе его эксплуатации.
Обычно выделяют три основных периода эксплуатации.
II – период нормальной эксплуатации – основной, наиболее длительный период эксплуатации, в течение которого работоспособность оборудования успешно поддерживается мероприятиями по техническому обслуживанию и техническому ремонту, а основную часть отказов составляют внезапные отказы, предотвращение которых путем своевременного обслуживания и ремонта невозможно, т.к. они обусловлены случайными внешними факторами, а замена неработоспособных элементов производится на такие же точно новые или отремонтированные, обладающие теми же недостатками (заложенными при проектировании и изготовлении), что и заменяемый элемент. Интенсивность отказов в этот период эксплуатации постоянна, а потому справедлив экспоненциальный закон распределения.
III – период интенсивного старения – интенсивность отказов возрастает по мере старения элементов технического изделия. Данный период имеет небольшую продолжительность.
Рассмотрим еще одно свойство экспоненциального закона - при
ятность безотказной работы составит R t e 1 0,368 , т.е. в данном случае, сред-
няя наработка до отказа – время, в течение которого вероятность безотказной работы уменьшается в « e » раз.

Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
Следует отметить, что показатели надежности определяются для номинального режима работы объекта (при 100% нагрузке), однако, на практике оборудование обычно эксплуатируется на меньших режимах. В теории надежности считается, что режим работы влияет только на безотказность и долговечность оборудования. Зависимость интенсивности отказов от режима работы объекта при условии неизменности закона распределения можно выразить следующим образом:
|
|
реж ном K режзn , |
(4.14) |
где K режз |
N реж |
- коэффициент загрузки объекта, |
n - опытный коэффициент, |
|
|||
|
Nном |
|
|
лежащий для механического оборудования в пределах 2 n 5 .
Таким образом, даже незначительное снижение нагрузки может привести к ощутимому повышению надежности. При этом справедливо и обратное утверждение, поэтому возможности перегрузки оборудования жестко регламентируются по величине и времени эксплуатации. Необходимо отметить, что снижение нагрузки в определенных пределах является одним из способов повышения надежности. При этом следует учитывать, что при изменении режима работы сложного технического изделия может измениться характер закона распределения отказов, а также качественный состав самих отказов, что может привести не к повышению, а, наоборот, снижению показателей надежности по сравнению с номинальным режимом работы, что, характерно, например, для дизелей на режимах, меньших 50% от номинальной мощности, оборудования, допустимый температурный режим работы которых задан не только максимумом, но минимумом и т.д.
Нормальный закон распределения. Нормальное распределение (распределение Лапласа-Гаусса) достаточно широко используется в математической статистике и теории вероятностей: согласно центральной предельной теореме сумма большого числа независимых или слабозависимых случайных величин, каждая из которых вносит небольшой вклад в эту сумму, хорошо согласуется с нормальным распределением. Так ошибки измерений часто следуют нормальному распределению, нормальное распределение является предельным для многих распределений. В теории надежности нормальный закон распределения используется для описания надежности стареющего оборудования, т.е. когда интенсивность отказов с течением времени возрастает. Это является вполне обоснованным, учитывая тот факт, что на надежность сложного оборудования в реальных условиях эксплуатации влияет множество независимых или слабозависимых факторов.
Плотность распределения вероятности отказов при нормальном законе рас-
пределения имеет следующий вид: |
|
|
t T |
|
2 |
|
|
|||
a t |
|
1 |
|
|
|
|
|
|||
|
EXP |
|
ср |
|
|
, |
(4.15) |
|||
|
|
|
|
|
||||||
|
|
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
где - среднеквадратичное отклонение наработки до отказа и Tср - матема-
тическое ожидание наработки до отказа являются параметрами формы и масштаба распределения соответственно.
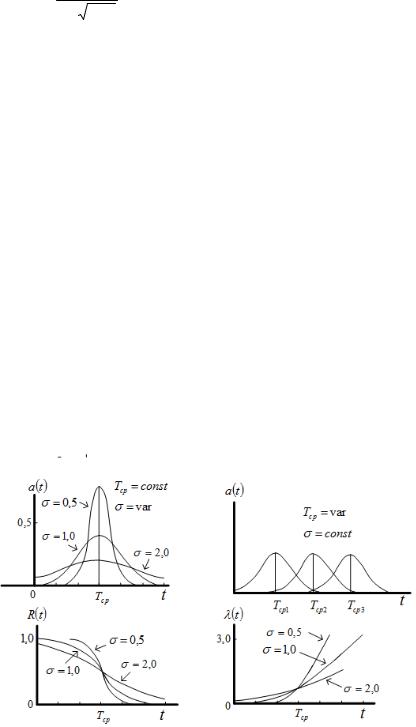
Кривые плотности нормального распределения симметричны и достигают
максимума, равного « |
1 |
» |
при « t Tср ». При удалении от «Tср » значения |
2 |
плотности уменьшаются и кривая асимптотически приближается к оси абсцисс. Зависимость вида плотности распределения от значений параметров распределения представления на рис 4.6.
Рассмотрим некоторые свойства нормального закона распределения. Если принять интервал времени равным (точки перегиба), тогда пло-
щадь над кривой плотности распределения, т.е. вероятность отказа будет равна
0,6827 (рис. 4.7).
Для интервалов Tср 2 ;Tср 2 и Tср 3 ;Tср 3 - 0,9545 и 0,9973 соответственно. Данным свойством пользуются, например, при назначении сроков технических обслуживаний и ремонтов. Так, если ремонт проводить в момент «Tср », то вероятность отказа до этого момента будет равна 1 0,6827 / 2 0,16 .
Аналогично для «Tср 2 » и «Tср 3 » получим 0,023 и 0,0014 . Следует отме-
тить, что в данном случае технические обслуживания и технические ремонты являются эффективными средствами повышения надежности. Действительно, так как отказавшие элементы заменяются точно такими же, технические обслуживания и технические ремонты не могут влиять на число внезапных отказов, но при этом отказы, возникновение которых в будущем возможно вследствие износа элемента полностью устраняются вместе с самим износом.
Рис. 4.6. Зависимость вида нормального распределения от значений параметров распределения

Основы надежности СЭУ, Чистяков А.Ю., 23.11.11 Закономерности распределения отказов
Рис. 4.7. Свойства нормального распределения
Вероятность отказа при нормальном законе распределения определится как: |
||||||||||
Q t |
1 |
|
t |
|
|
t T |
|
2 |
|
|
|
|
|
|
ср |
|
|
|
|||
|
|
EXP |
|
|
|
|
dt . |
(4.16) |
||
|
|
2 |
2 |
|
||||||
|
2 |
|
|
|
|
|
|
|
||
Данная формула не выражается через элементарные функции, поэтому его вычисляют через специальные функции, выражающие определенный интеграл
t2
от « e t2 » или « e 2 ». В теории надежности наиболее широко используются две функции: функцию распределения простейшего закона F x и нормированную
функцию Лапласа Ф x , для которых составлены таблицы [7] (Приложение 4). Опуская выводы, вероятность отказа можно записать в виде:
t T |
|
, |
(4.17) |
|
Q t F |
ср |
|
||
|
|
|
|
|
|
|
|
|
|
где F x 12 Ф x .
Учитывая, что:
F x 1 F x 12 Ф x ,
возможно определить вероятность безотказной работы:
|
|
|
|
T |
|
t |
|
|
|
|
|
|
|||
|
|
|
|
|
ср |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
R t 1 Q t F |
|
|
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интенсивность отказов определится как: |
t T |
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
EXP |
|
|
|
|
ср |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
a t |
|
|
|
|
|
2 |
2 |
|
|
|
||||
t |
|
|
|
|
|
|
|
. |
|||||||
R t |
|
|
|
|
T |
|
t |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
ср |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
F |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(4.18)
(4.19)
(4.20)
