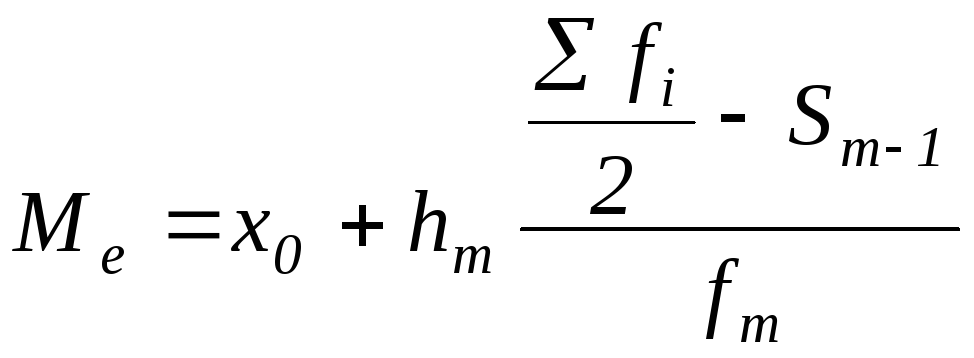Стат_Лекция 06

Лекция 6. Средние величины

Средние величины – это обобщающие показатели, выражающие типичные размеры количественно изменяющихся признаков качественно однородных явлений; характеризуют общий уровень этого признака, отнесенный к единице совокупности. Она применяется в случаях перехода от конкретных значений признака к характеристике всей совокупности.

В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования различают следующие виды средних:

1. среднеарифметическая;

2. среднегармоническая;

3. среднеантигармоническая;

4. среднестепенная;

5. среднеквадратическая;

6. распределительные средние:

- мода;

- медиана;

7. среднехронологическая.

1. Средняя арифметическая простая ()равна сумме произведений значений признака, деленной на их количество.

(13)

где Х₁,Х₂…Х_n- значение признака;

n – число значений признака.

Исходные данные для расчета простой среднеарифметической приведены в таблице 13.

Таблица 13. Данные для расчета простой среднеарифметической

Рабочие	Месячная заработная плата ( руб.)
1 2 3 4 5 6	1360 1840 1520 1840 1520 1840

По приведенным данным необходимо определить среднюю заработную плату одного рабочего бригады. Для этого просуммируем зарплату всех рабочих (значение признака) и разделим на количество рабочих (число значений признака):

руб.

Среднеарифметическая взвешенная может быть определена двумя способами: прямым – отношением суммы произведений значений признака на их частоту, на сумму частот, и способом «От нуля».

Прямым способом среднеарифметическая взвешенная () определяется по формуле:

(14)

где – частота, т. е. число случаев возникновения того или иного значения признака.

Исходные данные для расчёта среднеарифметической взвешенной приведены в таблице 14.

Таблица 14. Данные для исчисления среднеарифметической взвешенной прямым способом и способом «от 0»

Месячная заработная плата, руб.	Число рабочих	Х 	Отклонение значений признака Х от условной средней ряда, (1520), принятой за 0 Способ (от 0)	(Х-Х0) ×
Х			Х – Х0
1360 1520 1840	1 2 3	1360 3040 5520	-160 0 +320	-160 0 960
Итого	6	9920	-	800

Подставляя в вышеприведенную формулу полученные значения, определим среднеарифметическую среднюю прямым способом:

=9920/6=1653 руб/чел.

Способом «от нуля» среднеарифметическая может быть исчислена по формуле:

,

(15)

где Х₀ – значение признака, принятого за «0». За «0» обычно принимается значение признака, расположенного в середине вариационного ряда (В нашем примере Х₀ = 1520 руб). Поэтому ряд необходимо стараться сделать нечётным. При чётном количестве значений ряда, за «0», может быть принято значение признака с наибольшей частотой.

– условная среднеарифметическая, определяемая отношением суммы отклонений значений признаков от значения признака, принятого за «0», умноженной на соответствующие частоты, к сумме частот, по формуле:

= = 800/6 = 133 руб.

(16)

Среднеарифметическая, в этом случае, составит = 1520 + 133 = 1653 руб/чел., то есть имеет ту же величину, что полученная «прямым способом».

Приведём ещё пример расчета среднеарифметической способом «от 0» (табл. 15).

Таблица 15. Пример исчисления среднеарифметической способом «от 0»

Месячная заработная плата, руб.	Число рабочих	Отклонение значений признака от условной средней (от 0)	(Х-Х0) f
Х	f	Х – Х0
2500 2000 2340 2500 3000	11 20 23 32 14	-840 -340 0 +160 +500	-9240 -6400 0 +5060 +7000
Итого	100	-	-3580

За «0» принимаем значение признака, расположенного в середине вариационного ряда ( В нашем примере Х₀ = 2340 руб).

= -3580/100 = -35,8 руб., отсюда 2340 – 35,8 = 2304,2 руб.

2. Среднегармоническая определяется в тех случаях, когда:

• известны значения признака Х_i и произведение Х_if_i , а частота f_i не известна.

• в расчетах используются «обратные» показатели (например, вместо прямого показателя – производительность труда обратный ему – трудоёмкость, вместо фондоотдачи – фондоёмкость, вместо материалоотдачи – материалоёмкость и т.п.)

Для исчисления среднегармонической Х_if_i обозначим M_i , т.е. Х_if_i = M_i, отсюда f_i = M_i/Х_i . Преобразуем формулу среднеарифметической – вместо Х_if_i подставим M_i и получим среднеарифметическую взвешенную, исчисленную гармоническим способом:

(17)

В случаях, когда произведение X_if_i одинаково или равно единице (M_i = 1), применяется среднегармоническая простая, определяемая по формуле:

(17а)

Пример расчёта среднегармонической в случае, когда обобщаются «обратные» значения варьирующего признака (например, трудоемкость) приведен в таблице 16.

Таблица 16. Пример исчисления средней гармонической взвешенной

Трудоемкость продукции, чел.-ч, 1/Х	Число рабочих, f	Xifi
0,9 0,95 1,01 1,2 1,25	5 7 10 5 3	4,5 6,65 10,1 6,0 3,75
Итого	30	30,90

= 30/30,9= 0,97.

Средняя трудоемкость продукции равна 0,97 чел.-ч.

3. Для характеристики некоторых процессов подходит еще одна своеобразного вида средняя, так называемая антигармопическая. Формула ее такова:

(18) (18а)

Приведем примеры ее использования.

1, Имеется п учителей, и каждый подготовил k_i, учеников. Если каждый ученик подготовит столько же учеников, сколько подготовил его учитель, то среднее соотношение учеников и учителей (т. е. как бы производительность работы учителя или темп распространения знаний) выразится средней антигармонической. Пусть 6 учителей подготовили соответственно 8, 7, 14, 23, 15, 11 учеников. Тогда

2. Имеется п отраслей, k_i, – эффективность вложений в отрасль i, т. е. 1 руб. вложений в текущем году дает доход k_i рублей в следующем году. Если k_i – неизменны, то эффективность вложений Е выразится средней антигармонической, т. е.

.

(18б)

Допустим, имеются три отрасли. Пусть вложения в них имеют эффективность соответственно k₁ = 1,1; k₂ = 1,2 и k₃ = 1,4. Тогда

.

3. Имеется некоторая совокупность людей. Среди них п женщин. Пусть k_i – число детей у женщины. Предположим, что каждая дочь имеет столько же детей, сколько имела ее мать. Предположим, что число девочек равно числу мальчиков. Тогда соотношение численности между поколениями выразится средней антигармонической:

.

(18в)

Пусть у десяти женщин соответственно по 1, 2, 3, 2, 3, 5, 1, 1, 2, 4 детей. Тогда

Таким образом, на каждого человека первого поколения будет приходиться в среднем 3,083 человека следующего поколения.

4. Степенная средняя используется в случаях, когда определяется среднее значение, выраженное функцией к-го порядка. Частным случаем ее является среднеквадратическая.

5. Среднеквадратическая применяется в случае, когда осредняемое значение признака выражено в виде квадратных функций.

Степенная средняя и среднеквадратическая может быть простой и взвешенной и исчисляется соответственно по формулам:

(19, 20) (19а, 20а)

Имеется 10 квадратов с различной длиной сторон. Необходимо определить среднюю сторону одного квадрата (табл. 17).

Таблица 17. Исходные данные для расчета среднеквадратической. :

Сторона квадрата, см., (Х)	Количество квадратов, (f)	Х2	Х2  fi
4 6 8 10	1 3 5 1	16 36 64 100	16 108 320 100
Итого	10	-	544

Средняя сторона одного квадрата определится как среднеквадратическая взвешенная по формуле:

см.

6. Среднегеометрческая характеризует средний уровень относительных рядов динамики и исчисляется по формуле:

(21)

где n – число относительных величин динамики;

- относительная величина динамики цепная;

- относительная величина динамики базисная.

Исходные данные для расчета средней геометрической приведены в таблице 18.

Таблица 18. Исходные данные для расчета средней геометрической

Год	Товарная продукция, тыс. руб.	Относительные величины динамики (Темпы роста) %
		Цепные	Базисные
1 2 3 4 5	381 386 396 396 404	- 101,3 102,6 100,0 100,5	100,0 101,3 103,9 103,9 106,0

Необходимо определить среднегодовое увеличение товарной продукции за пятилетие. Для этого исчисляется средняя геометрическая

или 1,5%.

7. Распределительные средние включают моду и медиану.

Мода характеризует центр распределения по «весу» статистических единиц.

В дискретном ряду модой будет значение признака, частота которого наибольшая.

В интервальном ряду мода (М₀) находится в пределах того интервала, частота которого наибольшая (таблица 19).

Таблица 19. Исходные данные для расчета моды

Месячная заработная плата одного рабочего, руб.	Число рабочих
До1500 1500-1600 1600-1700 1700-1800 свыше1800	3 10 12 3 2

Моду находим по формуле:

(22)

где x_o – начало модального интервала;

h_{m –} величина модального интервала;

f_{m –} частота модального интервала;

f_{m-1 –} частота интервала, предшествующая модельному;

f_{m+1 –} частота интервала, следующего за модальным.

Мода находится в интервале от 1500 до1700 руб., т.к. его частота наибольшая, отсюда:

М₀ = 1600 + 100  = 1600+100=1600+18=1618 руб.

Медиана – вариант, занимающий среднее место в вариационном ряду и делящий его на две равные части.

В дискретном ряду медианным вариантом будет вариант, расположенный в середине вариационнного ряда и делящий его на две равные части. Для нахождения медианы необходимо предварительно определить номер медианного варианта (NM_e). В дискретном ряду с нечетной суммой частот, (NM_e) исчисляется следующим образом:

, (23)

где – сумма частот.

При четном числе частот имеют место два медианных варианта (NM_e¹ , NM_e² ), номера которых определяются следующим образом:

(23а,б)

Медианным вариантом будет тот вариант, с прибавлением частот которого сумма частот будет больше номера медианы. Следовательно, для определения медианного варианта необходимо последовательно суммировать частоты (таблица 20).

Таблица 20. Исходные данные для определения медианы в дискретном ряду

Месячная заработная плата одного рабочего, руб.	Количество рабочих, чел.	Последовательное суммирование частоты
1250 1570 1620 1650 1700 1850	10 15 17 20 15 5	10 10+15=25 25+17=42
Итого	82

Определяем номера вариантов:

NMe¹ = 82/2 = 41 и NMe² = 82/2 + 1 = 42.

После чего последовательно суммируем частоты (то есть, определяем накопленные частоты до размера медианных вариантов). Тогда, медиана, (при N = 42 = накопленной частоте), составит 1620 тыс. руб.

Для определения медианы в интервальном ряду предварительно определяют медианный интервал (х₀) точно также, как и медиану в дискретном ряду. Затем определяют медиану (Me) по формуле:

(24)

где x_o-начало медианного варианта;

h_m- величина медианного интервала;

- сумма частот;

S_m-1- сумма частот интервалов, предшествующих медианному;

f_m- частота медианного интервала.

Исходные данные для расчета медианы в интервальном ряду приведены в таблице 21.

Таблица 21. Исходные данные для расчета медианы в интервальном ряду

Выполнение нормы выработки, %	Число рабочих	Последовательное суммирование частот
До150 150-170 170-190 190-210 свыше 210	3 10 12 3 2	3 10+3=13 13+12=25
Итого	30

Определяем номера медианного интервала:

NM_e¹ = 30/2 = 15 NM_e² = 30/2 + 1 = 16.

Затем последовательно суммируем частоты. Медиана находится в интервале от 170 до 190% и определяется по формуле 3.9.

M_G=170+10=170+10=171,67%

ВОПРОСЫ ПО ЛЕКЦИИ 6.

1. Какими способами возможно определить среднюю арифметическую взвешенную

а) прямым методом: как отношение суммы произведений значений признаков на их частоты к сумме частот

б) методом моментов

в) методом наименьших квадратов

г) методом сумм

д) методом «от нуля»

2. В каких случаях рассчитывается среднегармоническая

а) когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны-

б) когда рассматриваются «обратные» значения признака

в) когда необходимо рассчитать распределение явления в среде

г) когда требуется получить новые значения признака

д) когда определяются суммарные значения признака

3. Для каких целей определяется средняя антигармоническая

а) когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны

б) когда рассматриваются «обратные» значения признака

в) когда необходимо рассчитать распределение явления в среде

г) когда требуется получить новые значения признака

д) когда определяются суммарные значения признака

4. В каких случаях рассчитывается степенная средняя

а) когда определяется среднее значение линейного вида

б) когда рассчитывается сумма произведений значений признаков на их частоты

в) когда определяется среднее значение, выраженное функцией n-ого порядка

г) когда рассчитывается сумма произведений значений признаков n-ого порядка на их частоты

д) когда определяется среднее значение нелинейного вида

5. Для каких целей определяется среднегармоническая

а) для определения среднего значения ряда динамики

б) для выявления относительной величины ряда

в) для расчета темпов роста явления