Лекции физика

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ - vt

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

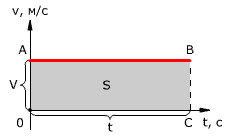Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

v = s₁ / t₁ = tg α

где α – угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

tg α₁ > tg α₂

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

tg α₃ = v₃ < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х = х₀

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Связь угловых и линейных величин

Отдельные точки вращающегося тела имеют различные линейные скорости . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости определяется скоростью вращения тела и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени тело повернулось на угол (рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный

Линейная скорость точки по определению.

(2.6)

Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:

подставляя значение скорости из (2.6), находим:

(2.7)

Тангенциальное ускорение

Воспользовавшись тем же отношением (2.6) получаем

(2.8)

Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.

Основные понятия.

Периодическим колебанием называется процесс, при котором система (например, механическая) возвращается в одно и то же состояние через определенный промежуток времени. Этот промежуток времени называется периодом колебаний.

Возвращающая сила - сила, под действием которой происходит колебательный процесс. Эта сила стремится тело или материальную точку, отклоненную от положения покоя, вернуть в исходное положение.

В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) колебания и вынужденные колебания.

Свободные колебания имеют место тогда, когда на колеблющееся тело действует только возвращающая сила. В том случае, если не происходит рассеивания энергии, свободные колебания являются незатухающими. Однако, реальные колебательные процессы являются затухающими, т.к. на колеблющееся тело действуют силы сопротивления движению (в основном силы трения).

Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которую называют вынуждающей. Во многих случаях системы совершают колебания, которые можно считать гармоническими.

Гармоническими колебаниями называют такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса:

(7.1)

Для иллюстрации физического смысла рассмотрим окружность, и будем вращать радиус ОК с угловой скоростью ω против часовой (7.1) стрелки. Если в начальный момент времени ОК лежал в горизонтальной плоскости, то через время t он сместится на угол . Если начальный угол отличен от нуля и равен φ₀, тогда угол поворота будет равен Проекция на ось ХО₁ равна . По мере вращения радиуса ОК изменяется величина проекции, и точка будет совершать колебания относительно точки - вверх, вниз и т.д. При этом максимальное значение х равно А и называется амплитудой колебаний; ω - круговая или циклическая частота; - фаза колебаний; – начальная фаза. За один оборот точки К по окружности ее проекция совершит одно полное колебание и вернется в исходную точку.

Периодом Т называется время одного полного колебания. По истечению времени Т повторяются значения всех физических величин, характеризующих колебания. За один период колеблющаяся точка проходит путь, численно равный четырем амплитудам.

Угловая скорость определяется из условия, что за период Т радиус ОК сделает один оборот, т.е. повернется на угол 2π радиан:

или

Частота колебаний - число колебаний точки в одну секунду, т.е. частота колебаний определяется как величина, обратная периоду колебаний:

Пружынный маятник упругие силы.

Пружинный маятник состоит из пружины и массивного шара, насаженного на горизонтальный стержень, вдоль которого он может скользить. Пусть на пружине укреплен шарик с отверстием, который скользит вдоль направляющей оси (стержня). На рис. 7.2,а показано положение шара в состоянии покоя; на рис. 7.2,б - максимальное сжатие и на рис. 7.2,в -произвольное положение шарика.

Под действием возвращающей силы, равной силе сжатия, шарик будет совершать колебания. Сила сжатия F = -kx , где k - коэффициент жесткости пружины. Знак минус показывает, что направление силы F и смещение х противоположны. Потенциальная энергия сжатой пружины

кинетическая .

Для вывода уравнения движения шарика необходимо связать х и t. Вывод основывается на законе сохранения энергии. Полная механическая энергия равна сумме кинетической и потенциальной энергии системы. В данном случае :

. В положении б) : .

Так как в рассматриваемом движении выполняется закон сохранения механической энергии, можно записать:

. Определим отсюда скорость:

Но в свою очередь и, следовательно, . Разделим переменные . Интегрируя это выражение, получим: ,

где - постоянная интегрирования. Из последнего следует, что

(7.2)

Сравнивая (7.1) с (7.2), получаем

(7.3)

Таким образом, под действием упругой силы тело совершает гармонические колебания. Силы иной природы, чем упругие, но в которых выполняется условие F = -kx, называются квазиупругими. Под действием этих сил тела тоже совершают гармонические колебания. При этом:

смещение:
скорость:
ускорение:

Математический маятник.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы относительно точки О: , и момент инерции: M = FL . Момент инерции J в данном случае Угловое ускорение:

С учетом этих величин имеем:

или

(7.8)

Его решение ,

где и

(7.9)

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

Затухающие колебания.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(7.17)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ

или

(7.18)

Перепишем это уравнение в следующем виде:

и обозначим:

где представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(7.19)

Будем искать решение уравнения (7.19) в виде где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение тогда С вещественным ω решением этого уравнения, как мы знаем, является функция

Таким образом, в случае малого сопротивления среды , решением уравнения (7.19) будет функция

(7.20)

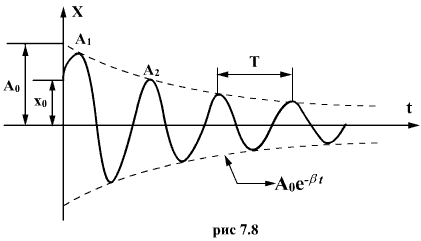
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

Вынужденные колебания.

В случае вынужденных колебаний система колеблется под действием внешней (вынуждающей) силы, и за счет работы этой силы периодически компенсируются потери энергии системы. Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы Определим амплитуду вынужденных колебаний тела массой m, считая колебания незатухающими вследствие постоянно действующей силы .

Пусть эта сила изменяется со временем по закону , где амплитуда вынуждающей силы . Возвращающая сила и сила сопротивления Тогда второй закон Ньютона можно записать в следующем виде:

или

(7.21)

Предположим, что возникающее под действием силы установившиеся вынужденные колебания системы также являются гармоническими: (7.22) причем их циклическая частота равна циклической частоте ω вынуждающей силы.

Дифференцируя два раза (7.22) и подставляя в (7.21), получим

Обозначим:

Тогда последнее равенство можно записать в следующем виде:

Правую часть этого выражения можно рассматривать как уравнение некоторого гармонического колебания, получившегося при сложении трех гармонических колебаний, определяемых слагаемыми левой части этого равенства. Для сложения этих колебаний воспользуемся методом векторных диаграмм. Проведем опорную линию ОХ (рис. 1.9) и отложим под углами, соответствующими начальным фазам всех четырех колебаний векторы , , , их амплитуды таким образом, чтобы

Из рис. 7.9 видно, что Подставляя в последнее значения соответствующих амплитуд (1.22), получим:

отсюда

(7.23)

Амплитуда установившихся вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы F₀, обратно пропорциональна массе m системы и уменьшается с увеличением коэффициента затухания β. При постоянных F₀, m и β амплитуда зависит только от соотношения циклических частот вынуждающей силы β и свободных незатухающих колебаний системы . При циклической частоте вынуждающей силы ω=0 амплитуда колебаний . В этом случае колебания не совершаются и смещение при вынужденных колебаниях равно статической деформации под действием постоянной силы F₀:

Поэтому отклонение A₀ иногда называют статической амплитудой.

Если нет диссипации т.е β=0, то амплитуда колебаний

растет с увеличением циклической частоты ω вынуждающей силы F_вн и при становится бесконечно большой (рис. 7.10). При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем

Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы называется резонансом.

Если затухание существует то амплитуда вынужденных колебаний достигает максимального значения, когда знаменатель правой части для уравнения (7.23) достигает минимума. Приравнивая нулю первую производную по ω от подкоренного выражения, получим условие его минимума, для которого , где - называют резонансной частотой. обозначает то значение циклической частоты ω вынуждающей силы, при котором .

Из последней формулы следует, что для консервативной системы , а для диссипативной системы несколько меньше собственной циклический частоты. С увеличением коэффициента затухания ω явление резонанса проявляется все слабее, и, наконец при исчезает совсем.