Свойства обратной матрицы:

1. |A^1| = ;

2. (AB)^1 = B^1A^1;

3. (A^1)^т = (А^т)^1.

2. Алгебра многочленов. Наибольший общий делитель двух многочленов (алгоритм Евклида).

Многочленом n-ой степени называется функция вида

,

где – постоянные коэффициенты (действительные или комплексные), а – комплексная переменная, которая может принимать любые комплексные значения или, выражаясь геометрическим языком, может быть любой точкой комплексной плоскости.

Если при , то число называется корнем или нулем многочлена .

Для многочленов определены следующие арифметические операции:

В результате операций 1) и 2) снова получится многочлен. Частное двух многочленов может не быть многочленом.

Деление многочленов с остатком.

,

,

где – частное, а – остаток.

Теорема Безу.

Для того, чтобы многочлен имел (комплексный) корень , необходимо и достаточно, чтобы он делился на , т.е. чтобы его можно было представить в виде произведения , где – некоторый многочлен степени n-1.

Если при разложении , то на основании теоремы Безу применимой к , многочлен не делится на , а хотя и делится на , но не делится на . В этом случае говорят, что – простой корень (нуль) многочлена .

Пусть теперь . Тогда по теореме Безу, применимой к , многочлен делится на , и мы получим , где – некоторый многочлен степени n-2. Если , то делится на , но не делится на , и тогда число называется корнем (нулем) кратности 2.

В общем случае для некоторого натурального имеет место

,

где – многочлен степени n-s, и тогда говорят, что – корень (нуль) многочлена кратности s.

Теорема Гаусса (основная теорема алгебры).

Всякий многочлен n-ой степени (ненулевой, т.е. ) имеет по крайней мере один комплексный корень (нуль).

Следствие из теоремы Гаусса.

Многочлен n-ой степени со старшим не равным нулю коэффициентом имеет n комплексных корней с учетом кратности, иначе говоря представляется в виде произведения

,

где – различные корни кратностей, соответственно .

Если у многочлена с вещественными коэффициентами есть комплексные корни, то они входят сопряженными парами, т.е. если – корень многочлена , то и корень будет являться корнем многочлена .

Раскладывая в разложении на квадратичные множители многочлена комплексные корни на сопряженные, т.е. получим разложение многочлена на линейные множители.

В результате получим разложение вида

,

где отвечает вещественному корню b кратности l, а – комплексным корням и кратности m.

Наибольший общий делитель многочленов

Пусть даны произвольные многочлены и . Многочлен будет называться общим делителем для и , если он служит делителем для каждого из этих многочленов. Свойство 5. показывает, что к числу общих делителей многочленов и принадлежат все многочлены нулевой степени. Если других общих делителей эти два многочлена не имеют, то они называются взаимно простыми.

В общем же случае многочлены и могут обладать делителями, зависящими от , и введем понятие о наибольшем общем делителе этих многочленов.

Наибольшим общим делителем отличных от нуля многочленов и называется такой многочлен , который является их общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов. Обозначается наибольший общий делитель многочленов и символом .

Это определение оставляет открытым вопрос, существует ли наибольший общий делитель для любых многочленов и . Ответ на этот вопрос положительный. Существует метод для практического разыскания наибольшего общего делителя данных многочленов, называемый алгоритмом последовательного деления или алгоритмом Евклида.

Алгоритм Евклида – метод для нахождения наибольшего общего делителя двух целых чисел, а также двух многочленов от одного переменного. Он первоначально был изложен в «Началах» Евклида в геометрической форме как способ нахождения общей меры двух отрезков. Алгоритм Евклида для нахождения наибольшего общего делителя, как в кольце целых чисел, так и в кольце многочленов от одного переменного является частным случаем некого общего алгоритма в евклидовых кольцах.

Алгоритм Евклида для нахождения наибольшего общего делителя двух многочленов и состоит в последовательном делении с остатком на , затем на первый остаток , затем на второй остаток и так далее. Так как степени остатков все время понижаются, то в этой цепочке последовательных делений мы дойдем до такого места, на котором деление совершится нацело и процесс остановится. Последний отличный от нуля остаток , на который нацело делится предыдущий остаток , и является наибольшим общим делителем многочленов и .

Для доказательства запишем изложенное в виде следующей цепочки равенств:

Последнее равенство показывает, что служит делителем для . Отсюда следует, что оба слагаемых правой части предпоследнего равенства делятся на , а поэтому будет делителем и для . Далее, таким же путем, поднимаясь вверх, мы получим, что является делителем и для , …, , . Отсюда ввиду второго равенства, будет следовать, что служит делителем для , а поэтому, на основании первого равенства, - и для .

Возьмем теперь произвольный общий делитель многочленов и . Так как левая часть и первое слагаемое правой части первого из равенств делятся на , то также будет делится на . Переходя ко второму и следующему равенствам, таким же способом получим, что на делятся многочлены , , … Наконец, если уже будет доказано, что и делятся на , то из предпоследнего равенства получим, что делится на . Таким образом, на самом деле будет наибольшим общим делителем для и .

Мы доказали, что любые два многочлена обладают наибольшим общим делителем, и получили способ его вычисления. Этот способ показывает, что если многочлены и имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными, хотя у этих многочленов могут существовать и такие делители, не все коэффициенты которых рациональны (действительны).

Если есть наибольший общий делитель многочленов и , то в качестве наибольшего общего делителя этих многочленов можно было бы выбрать также многочлен , где - произвольное число, отличное от нуля. Иными словами, их наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени. Ввиду этого можно условиться, что старший коэффициент наибольшего общего делителя двух многочленов будет всегда считаться равным единице. Используя это условие можно сказать, что два многочлена тогда и только тогда взаимно просты, если их наибольший общий делитель равен единице. В самом деле, в качестве наибольшего общего делителя двух взаимно простых многочленов можно взять любое число, отличное от нуля, но, умножая его на обратный элемент, получим единицу.

Применяя алгоритм Евклида к многочленам с целыми коэффициентами, можем, чтобы избежать дробных коэффициентов, умножить делимое или сократить делитель на любое не равное нулю число, причем не только начиная какое-либо из последовательных делений, но и в процессе самого этого деления. Это будет приводить к искажению частного, но интересующие нас остатки будут приобретать лишь некоторый множитель нулевой степени, что при разыскании наибольшего общего делителя допускается.

3. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ (С.Л.У.). Линейная зависимость и независимость систем векторов. Подпространства. Линейная оболочка системы векторов. Базис и размерность. Теорема о размерности суммы двух подпространств. Теорема о размерности пространства решений однородной С.Л.У.

Понятие линейного пространства

Множество L называется линейным (векторным) пространством, если выполнены следующие условия:

1) В L введена операция сложения элементов, т.е. определено отображение (обозначение: ), обладающее следующими свойствами:

- ;

- ;

- (элемент 0 называется нулевым);

- (элемент –x называется противоположным элементу x);

2) В L введена операция умножения элементов на действительные (комплексные) числа, т.е. определено отображение (обозначение: ), обладающее следующими свойствами:

- ;

- ;

3) Операция сложения элементов и умножения их на числа удовлетворяют законам дистрибутивности:

- ;

- ;

Элементы линейного пространства называются векторами. Пространство L называется действительным, если в L операция умножения векторов на число определена только для действительных чисел, и комплексным, если эта операция определена для комплексных чисел.

Примеры линейных пространств:

1) – пространство геометрических векторов . :

- если , то ;

- если , то .

2) – арифметическое пространство.

– множество упорядоченных наборов из n вещественных чисел со следующими правилами:

,

,

3) – пространство многочленов.

,

,

4) – пространство ()-матриц.

(), ()

5) – пространство функций, непрерывных на .

,

,

,

Подпространством линейного пространства L называется такое подмножество , которое обладает свойствами:

1) ;

2) .

Выводы:

1) всякое подпространство содержит ;

2) каждый вектор в подпространство входит с противоположным.

Теорема 1.

Подпространство линейного пространства само является линейным пространством относительно операций сложения и умножения векторов на число.

является линейной комбинацией векторов системы S, если , где .

Совокупность линейных комбинаций векторов системы S из линейного пространства L называется линейной оболочкой, т.е.

Теорема 2.

Линейная оболочка системы S в линейном пространстве L образует подпространство в L.

Линейная оболочка системы – наименьшее подпространство, содержащее все векторы системы.

Линейная зависимость и независимость системы векторов

Система векторов называется линейно зависимой, если найдутся числа , не равные одновременно нулю и такие, что ; в противном случае эта система называется линейно независимой.

Свойства:

1) – линейно зависима, если ;

2) – линейно зависима, если ;

3) Если система содержит зависимую подсистему, то вся система зависима.

Следствия:

1) Всякая часть линейно независимой системы линейно независима;

2) Система, содержащая – линейно зависима;

3) Система, содержащая два равных или пропорциональных вектора, линейно зависима.

Критерий линейной зависимости.

Для того, чтобы система векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из ее векторов линейно выражался через другие.

Геометрический смысл линейной зависимости.

1) Система из 2-х векторов линейно зависима тогда и только тогда, когда они коллинеарны, т.е.

– линейно зависима, когда .

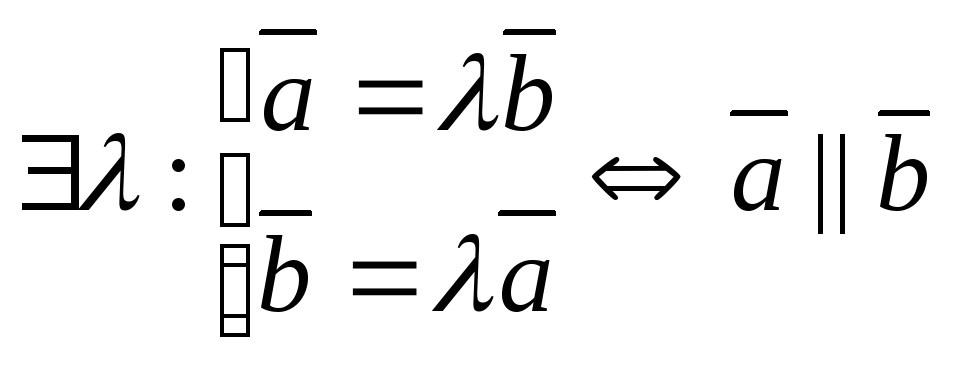Замечание: коллинеарен любому (каждому) вектору.

2) Система из 3-х векторов линейно зависима тогда и только тогда, когда они компланарны.

3) Любая система из 4-х и более векторов – линейно зависима.

Ранг системы векторов

Рангом системы векторов называется размерность ее линейной оболочки, т.е.

.

Подсистема системы называется базой в , если

1) – линейно независима;

2) Любой вектор из линейно выражается через векторы .

Сохранение ранга системы векторов при элементарных преобразованиях.

Пусть , а . Если все векторы линейно выражаются через векторы , то

Доказательство:

Т.к. и , то вышесказанное будет доказано, если докажем, что . Для любого имеет разложение , но каждый вектор линейно выражается через

,

, (*)

где и т.д.

Из (*) , , т.е. есть включение .

Элементарные преобразования системы векторов:

1) перестановка 2-х векторов;

2) умножение вектора на число, не равное 0;

3) добавление к одному вектору другого, умноженного на коэффициент.

Теорема.

При элементарных преобразованиях ранг сохраняется:

.

Пусть – система векторов из . Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов данной системы, т.е

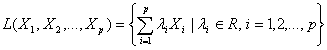
Свойства линейной оболочки: Если , то для и .

Линейная оболочка обладает свойством замкнутости по отношению к линейным операциям (операции сложения и умножения на число).

Базис и размерность линейного пространства.

Число n называется размерностью линейного пространства L, если:

1) в L существует система из n линейных векторов;

2) любая система из n+1 векторов в L – линейно зависима.

Замечание: В n-мерном пространстве L линейно зависима любая система из вектора.

Базисом n-мерного линейного пространства L называется всякая линейно независимая система в L, состоящая из n-векторов.

Базисы в линейных пространствах.

1) , .

Базис в L – любая тройка некомпланарных векторов. Канонический базис:

.

2) , .

Базис в L образует, например, . Канонический базис:

.

3) , .

4) , .

Канонический базис:

.

Определение Линейное пространство , в котором существует базис, состоящий из векторов, называется -мерным линейным или векторным пространством. Число называется размерностью пространства и обозначается . Линейное пространство, в котором не существует базис, называется бесконечномерным.

Примером бесконечномерного пространства является пространство всех многочленов с вещественными коэффициентами.

Теорема Пространство столбцов из элементов, являющихся вещественными числами, имеет рамерность .

Доказательство. Возьмем систему векторов

Покажем, что эта система линейно независима. Составим линейную комбинацию и приравняем ее к нулю:

Преобразуем левую часть:

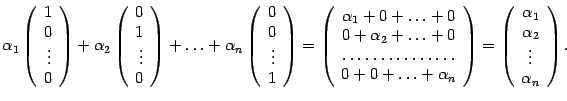
Следовательно,

откуда , , . Итак, система векторов -- линейно независима.

Пусть -- произвольный вектор пространства, 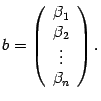Очевидно, что

Следовательно, вектор является линейной комбинацией векторов . Тем самым доказано, что векторы образуют базис в пространстве столбцов из элементов. Размерность пространства равна числу векторов в базисе. Следовательно, пространство -- -мерное.

4. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ. Матрица линейного преобразования конечномерного векторного пространства. Собственные значения и собственные векторы линейного преобразования, теорема о связи собственных значений линейного преобразования с корнями его характеристического многочлена.

Будем говорить, что на множестве векторов R задано преобразование А, если каждому вектору хR по некоторому правилу поставлен в соответствие вектор АхR.

Определение 1.1. Преобразование А называется линейным, если для любых векторов х и у и для любого действительного числа λ выполняются равенства:

А(х + у)=Ах + Ау, А(λх) = λ Ах. (1.1)

Определение 1.2. Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя.

Тождественное преобразование обозначается Е: Ех = х.

Рассмотрим трехмерное пространство с базисом е₁, е₂, е₃, в котором задано линейное преобразование А. Применив его к базисным векторам, мы получим векторы Ае₁, Ае₂, Ае₃, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса:

Ае₁ = а₁₁ е₁ + а₂₁ е₂ +а₃₁ е₃,

Ае₂ = а₁₂ е₁ + а₂₂ е₂ + а₃₂ е₃, (1.2)

Ае₃ = а₁₃е₁ + а₂₃ е₂ + а₃₃ е₃ .

Матрица называется матрицей линейного преобразования А в базисе е₁, е₂, е_{3 .} Столбцы этой матрицы составлены из коэффициентов в формулах (1.2) преобразования базиса.

Замечание. Очевидно, что матрицей тождественного преобразования является единичная матрица Е.

Для произвольного вектора х =х₁е₁ + х₂е₂ + х₃е₃ результатом применения к нему линейного преобразования А будет вектор Ах, который можно разложить по векторам того же базиса: Ах =х`<sub>1</sub>е<sub>1</sub> + х`₂е₂ + х`<sub>3</sub>е<sub>3</sub>, где координаты x`_i можно найти по формулам:

х`₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃,

x`₂ = a₂₁x₁ + a₂₂x₂ + a₂₃x₃, (1.3)

x`₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃.

Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.

Преобразование матрицы линейного преобразования при переходе к новому базису.

Рассмотрим линейное преобразование А и два базиса в трехмерном пространстве: е₁, е₂, е₃ и е₁, е₂, е_3. Пусть матрица С задает формулы перехода от базиса {e_k} к базису {e_k}. Если в первом из этих базисов выбранное линейное преобразование задается матрицей А, а во втором – матрицей А, то можно найти связь между этими матрицами, а именно:

А = С^-1АС (1.4)

Действительно, , тогда А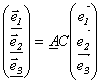. С другой стороны, результаты применения одного и того же линейного преобразования А в базисе {e_k}, т.е. , и в базисе {e_k}: соответственно - связаны матрицей С: , откуда следует, что СА=АС. Умножая обе части этого равенства слева на С^-1, получим С^-1СА = = С^-1АС, что доказывает справедливость формулы (1.4).

Собственные числа и собственные векторы матрицы.

Определение 1.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом матрицы А.

Подставив в формулы (1.3) x`_j = λx_j, получим систему уравнений для определения координат собственного вектора:

.

Отсюда

. (1.5)

Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

| A - λE | = 0, (1.6)

поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A - λE| называется характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

1) Характеристический многочлен линейного преобразования не зависит от выбора базиса.

Доказательство. (см. (1.4)), но следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.

2) Если матрица А линейного преобразования является симметрической (т.е. а_ij=a_ji), то все корни характеристического уравнения (1.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов х₁, х₂, х₃, соответствующих собственным значениям λ₁, λ₂, λ₃ матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

(1.7)

Доказательство этого свойства следует из определения собственных векторов.

2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

, откуда х₍₂₎={b,-b,b} или, при условии |x₍₂₎|=1, x₍₂₎=

Для λ₃ = 6 найдем собственный вектор x₍₃₎={z₁, z₂, z₃}:

, x₍₃₎={c,2c,c} или в нормированном варианте

х₍₃₎ = Можно заметить, что х₍₁₎х₍₂₎ = ab – ab = 0, x₍₁₎x₍₃₎ = ac – ac = 0, x₍₂₎x₍₃₎ = bc - 2bc + bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.

Пусть заданы два подпространства -мерного пространства . Обозначим их и .

Определение 1.8 Если каждый вектор пространства можно, и притом единственным образом, представить как сумму двух векторов

где , а , то говорят, что пространство разложено в прямую сумму подпространств и .

Это обычно записывают так:

Теорема 1.3 Для того чтобы пространство разлагалось в прямую сумму подпространств и , достаточно, чтобы:

1. Подпространства и имели только один общий вектор (нулевой вектор).

2. Сумма размерностей этих подпространств была равна размерности пространства .

Доказательство. Выберем некоторый базис в подпространстве и базис в подпространстве . Поскольку сумма размерностей и есть , то общее число этих векторов .

Покажем, что векторы

линейно независимы, т.е. образуют базис пространства . Действительно, пусть

отсюда

Левая часть этого равенства есть вектор из , а правая из . Так как, по условию, единственный общий вектор и есть нулевой вектор, то

Но каждый из наборов и состоит из линейно независимых векторов, так как это базисы в и . Поэтому из первого равенства (10) следует, что

а из второго следует, что

Следовательно, система состоит из линейно независимых векторов, т.е. это есть базис в пространстве .

Мы доказали, что при выполнении условий теоремы существует базис, первые векторов которого образуют базис в , а последние -- базис в .

Произвольный вектор из можно разложить по векторам этого базиса

При этом

и

Таким образом,

где и . Покажем, что это разложение единственно. Предположим, что существуют два разложения:

где

и

где

Вычитая второе равенство из первого, получаем:

откуда

Так как вектор, стоящий в левой части равенства, принадлежит , а вектор, стоящий в правой части, принадлежит , то каждый из этих векторов равен нулю, т.е.

Единственность разложения доказана.