Алгоритм Штрассена

Алгоритм Штрассена.

Содержание

1

1Вступление и постановка задачи

Одна из главных задач данной работы - реализовать алгоритм Штрассена. Это рекурсивный алгоритм для умножения матриц, который позволяет значительно ускорить процесс умножения. Надо заметить, что данный алгоритм эффективен только для матриц достаточно большого размера. Определить размер матриц, с которого имеет смысл начинать умножать по алгоритму Штрассена, можно экспериментальным путем. Кроме того, я уже упоминала, что алгоритм является рекурсивным. В нерекурсивной ветви алгоритма используется "простое"умножение матриц, т.е. умножение по определению. Сделать нерекурсивную ветвь наиболее эффективной и организовать выход из рекурсии в нужный момент - еще одна задача моей работы.

Итак, наметим цели работы:

Реализовать алгоритм Штрассена;

Экспериментально найти размер матрицы, для которого следует переходить на умножение по алгоритму;

Организовать выход из рекурсии в нужный момент;

Сделать не рекурсивную ветвь наиболее эффективной.

2Алгоритм Штрассена

Самая затратная по времени операция - умножение. Т.е. чтобы ускорить процесс, нужно сократить их число. Штрассен придумал алгоритм [1, 2, 3], который позволяет избежать одного умножения. Замечательно, что формулы не требуют коммутативности сложения, т.е. они приминимы и для матриц, что позволяет применять алгоритм рекурсивно.

Алгоритм работает с квадратными матрицами размера 2n. Заметим, что для умножения матриц такого размера требуется 23n умножений. Если же матрицы не квадратные, то можно расширить их до нужного размера, заполнив недостающие строки и столбцы нулями. Допустим, есть две матрицы A и B размера 2n, которые требуется перемножить: C = AB. Разобьем каждую матрицу на четыре подматрицы:

2

Тогда матрицы Ai;j и Bi;j имеют размер 2n 1. А элементы матрицы можно вычислить следующим образом:

C1;1 = A1;1B1;1 + A1;2B2;1

C1;2 = A1;1B1;2 + A1;2B2;2

C2;1 = A2;1B1;1 + A2;2B2;1

C2;2 = A2;1B1;2 + A2;2B2;2

Но в этом случае мы не уменьшили количество умножений, т.к. каждое уравнение требует двух умножений матриц размера 2n 1. А на каждом шаге рекурсии умножений получится восемь.

Штрассен ввел семь новых элементов, которые вычисляются с помощью одного умножения, а матрица C получается из них сложением или вычитанием. Определим эти семь элементов:

M1 = (A1;1 + A2;2)(B1;1 + B2;2)

M2 = (A2;1 + A2;2)B1;1

M3 = A1;1(B1;2 B2;2)

M4 = A2;2(B2;1 B1;1)

M5 = (A1;1 + A1;2)B2;2

M6 = (A2;1 A1;1)(B1;1 + B1;2)

M7 = (A1;2 A2;2)(B2;1 + B2;2)

Элементы матрицы C вычисляются по формулам:

C1;1 = M1 + M4 M5 + M7

C1;2 = M3 + M5

C2;1 = M2 + M4

C2;2 = M1 M2 + M3 + M6

Теперь на каждом этапе рекурсии требуется выполнять только семь умножений вместо восьми. Предполагается, что итерационный процесс продолжается 2n раз, до тех пор, пока матрицы Ci;j не выродятся в числа. Заметим, что для маленьких матриц алгоритм теряет свою эффективность. Также этот алгоритм не имеет большой устойчивости [3], т.е. для вещественных матриц, в случае, если нужна очень высокая точность, не

3

стоит умножать по Штрассену. Этот существенный минус легко объяснить большим количесвом сложений и вычитаний. Но для целочисленных матриц, конечно, проблемы не возникает.

Рекурсивный алгоритм Штрассена умножает две матрицы за время (n2:81) [1], тогда как простое умножение справляется с этой задачей за (n3). Для матриц большого размера(начиная примерно с 2000) эта разница существенна.

3Умножение матриц по определению, встроенная функция matmul и оптимизация

В этом разделе пойдет речь об умножении матриц без помощи алгоритма Штрассена. Прежде чем приступать непосредственно к алгоритму, нужно выяснить, нельзя ли ускорить процесс умножения с помощью других возможностей фортрана. Также в фортране есть специальная встроенная функция matmul, которая возвращает результат умножения двух матриц. Каким образом эта функция производит умножение, неизвестно. Попробуем написать код для умножения матриц по опредлению. Пусть A и B - умножаемые матрицы, а C - их произведение.

do i = 1, N

do j = 1, N C (i , j) = 0

do k = 1, N

C(i , j) = C(i , j) + A(i , k )* B(k , j)

end do

end do

end do

Назовем такой вариант def mul. Посмотрим, как быстро умножает матрицы matmul и как медленно происходит умножение по определению. В первой строке таблицы указан размер умножаемых матриц, во второй - время, за которое умножает matmul, а втретьей - время умножения по определению. Время указано в секундах, т.о. матрицы размера 2048 умножаются в первом случае - за 13 секунд, а во втором - за 15 минут!

Откуда возникает такая разница? В фортране обращение к элементам массива происходит по столбцам [4]. Т.е., к примеру, чтобы обратиться к первому элементу пятого столбца, компилятор сначала просчитает все впереди стоящие элементы по столбцам. Значит, имеет смысл попробовать переписать умножение так, чтобы индекс столбца менялся быстрее,

4

чем индекс строки. Для этого надо поменять внешний и внутренний циклы местами, а средний оставить на месте:

do k = 1, N

do j = 1, N

do i = 1, N

C(i , j) = C(i , j) + A(i , k )* B(k , j)

end do

end do

end do

Теперь к предыдущей таблице добавим результат получившейся программы, назовем ее def mul tr.

Нетрудно догадаться, что транпонировав одну из матриц, можно перемножать только столбцы, что еще сократит время умножения. Для транспонирования можно воспользоваться встроенной функцией transpose. Далее можно избавившись от одного цикла. Это позволяет сделать возможным описание сечений (в данном случае - столбцов) и использование встроенной функции сложения массивов sum. Тогда умножение двух матриц приобретёт вид:

A = transpose (A) do i = 1, N

do j = 1, N

C(j , i) = sum (A(: , j )* B(: , i ))

end do

end do

Посмотрим, на что способен такой вариант(его название - two loops mul):

Очевидно, что последний вариант - самый быстрый из рассмотренных, но он уступает matmul. Для наглядности ниже представлен график.

5

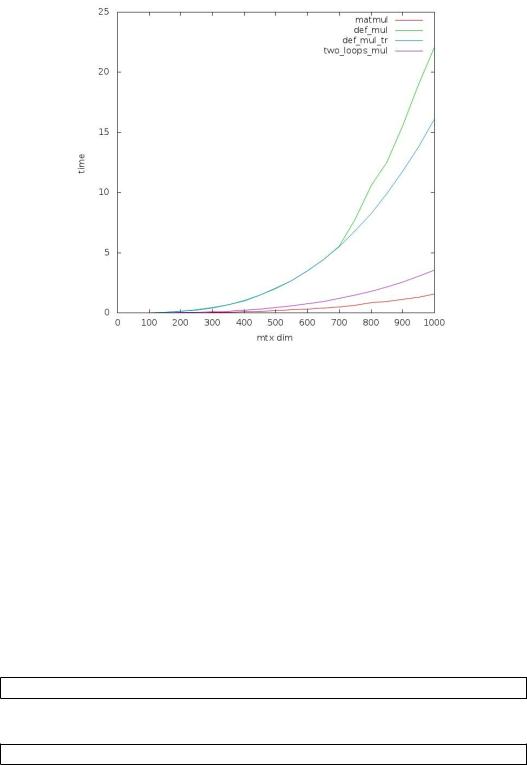
Чтобы усовершенствовать наш метод, нужно обратить внимание на компилятор. Что вообще такое компилятор? Это программа, которая переводит текст с языка программирования высокого уровня(в данном случае на Фортране) на язык машинного уровня. Компилятор позволяет осуществить связь между тем, что пишет программист, и процессором компьютера. Я пользуюсь компилятором GF ortran из GNU Compiler Collection, который позволяет оптимизировать компиляцию[5]. Существует несколько уровней оптимизации: O1; O2; O3; Ofast. Каждый имеет свои особенности, которые я не буду подробно описывать. Для умножения матриц и алгоритма Штрассена лучше всего подходит уровень Ofast, т.к. он включает в себя наибольшее количество опций и является самым быстрым. Также можно использовать опцииmarch = native и mtune = native [6], которые генерируют код для указанной архитектуры процессора. На место native компилятор сам ставит значение, соответствующее данному процессору.

До этого момента я использовала стандартную компиляцию:

gfortran -o test_mul test_mul . f90

А теперь при компиляции добавлю вышеописанные опции. Тогда компиляция будет выглядеть так:

gfortran -o test_mul - Ofast - mtune = native - march = native test_mul . f90

6

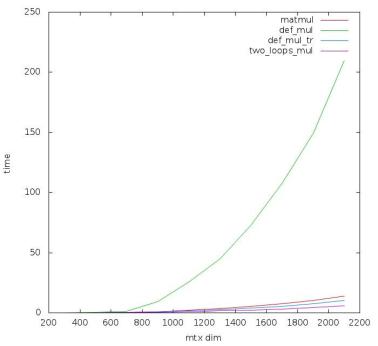
Посмотрим, как изменятся результаты:

7

Matmul занял на этот раз третье место, и время его работы почти не изменилось. Это объясняется тем, что эта встроенная функция уже скомпилирована, а вот написанные мной программы - нет, и на них опции компиляции влияют очень сильно. Теперь первое место в таблице занимает умножение с двумя циклами, второе место досталось умножению по столбцам, а умножение по определению занимает почётное последнее место. Последние результаты показывают, что преуспеть можно и без алгоритма Штрассена, а лишь используя знания о том, как устроен язык программирования. Опции компилятора Ofast; mtune = native; march = native сыграли решающую роль в оптимизации, что говорит о том, насколько важно собирать программу под конкретный процессор. В дальнейшем я всегда буду использовать эти три опции. Самое быстрое умножение с двумя циклами лучше всего подойдет для нерекурсивной ветви алгоритма Штрассена, так что часть задачи уже решена.

4Реализация алгоритма

В ходе своей работы я придумала несколько вариантов реализации алгоритма Штрассена. Хотя эти варианты очень похожи, каждый их них имеет свои преимущества и недостатки. Так как алгоритм работает только с квадратными матрицами, размер которых два в натуральной степени, то

8

все остальные матрицы нужно пополнить до нужного размера нулевыми строками и столбцами. Как это будет реализовано непосредственно на языке программирования, не имеет значения. После совершения этой операции мы можем иметь дело с матрицами любого размера. Написать рекурсивную подпрограмму, выполняющую алгоритм Штрассена, не очень сложно: для этого надо просто воспроизвести все то, что описано в соответствующем разделе, на языке программирования. Пусть есть две матрицы A и B, заполненные случайными числами, которые требуется перемножить, и пусть эти матрицы уже имеет размер 2n, а матрица C - результат умножения. В ходе алгоритма потребуется семь новых элементов M1 M7, которые будут вычисляться рекурсивно. Пока оставим вопрос о том, начиная с какого номера лучше выходить из рекурсии, будем умножать по алгоритму, пока матрица не станет размера 8 8.

9

P=N /2

allocate ( A11 (P ,P), A12 (P ,P), A21 (P ,P), A22 (P ,P )) allocate ( B11 (P ,P), B12 (P ,P), B21 (P ,P), B22 (P ,P ))

allocate ( M1 (P ,P), M2 (P ,P), M3 (P ,P), M4 (P ,P )) allocate ( M5 (P ,P), M6 (P ,P), M7 (P ,P ))

deallocate (A11 , A12 , A21 , A22 , B11 , B12 , B21 , B22 )

Разберем тут же еще один вариант. Этот вариант не предполагает объявления семи матриц M1 M7, и тогда четыре блока матрицы C можно найти следующим образом:

10