
Лекция-5
.pdfЛекция № 5
Гидродинамика (механика жидкости)
I. Особенности расположения молекул в жидкости
Жидкость - одно из трёх агрегатных состояний вещества (не считая 4-го состояния, называемого "плазма", в котором пребывает "всего" 99,5% веще-
ства во Вселенной в виде звёзд). Все агрегатные состояния вещества разли-
чаются организацией молекул. В отличие от твёрдого (кристаллического) со-
стояния, характерного строго упорядоченным расположением частиц веще-
ства, в жидкости нет дальнего (распространяющегося на весь кристалл) по-
рядка расположения атомов (молекул). Для организации молекул жидкости характерен виртуальный (т.е. недолговечный) "ближний порядок". Это зна-
чит, что в жидком состоянии вещества молекулы группируются небольшими
"коллективами", причём время жизни молекулы в данном "коллективе" очень непродолжительно (~10-11с). Затем следует переход в другой "коллектив".
Жидкое состояние является промежуточным между твёрдым и газообраз-
ным состояниями вещества. Расстояние между молекулами в газах во много раз превышает размеры молекул; в жидкости молекулы размещены вплотную друг к другу, со средним расстоянием между их центрами порядка размера молекулы (т.е. 10 100 A =(10 100) 10-10 м. Поэтому, плотности жидкостей на несколько порядков больше плотностей газов (при нормальном давлении)
и почти не отличаются от плотностей твёрдых тел; так, плотность металлов при плавлении меняется (уменьшается) в среднем на 3%.
Основные свойства жидкостей:
1) текучесть; объясняется преимущественными перескоками молекул из одного "коллектива" в другой в направлении действия внешней силы (напри-
мер, силы тяжести); если внешние силы скомпенсированы, то перескоки мо-
лекул из одного положения равновесия ("коллектива") в другое происходят с одинаковой частотой и жидкое тело сохраняет свою форму;
49
2) несжимаемость (по сравнению с газами); объясняется достаточно плотным расположением молекул в жидкости. Примеры: а) удар молотом по полому металлическому ядру, заполненному жидкостью поверхность ядра покрывается "испариной"; б) "потение" цилиндров гидравлических машин;
в) при оказании на воду давления в 100 атмосфер (что имеет место в морях на глубине 1 км) её плотность увеличивается всего на 0,5%.
II. Уравнение неразрывности струи
Различают два вида течения реальной жидкости: 1) ламинарное (слоистое),
когда в потоке жидкости её слои, скользя относительно друг друга, не пере-
мешиваются между собой; 2) турбулентное (вихревое), когда в потоке жид-
кости происходит интенсивное вихреобразование и перемешивание слоёв.
Линии тока – линии, касательные к которым в каждой точке потока совпа-
дают с направлением скорости частиц жидкости; поэтому при ламинарном течении траектории частиц жидкости совпадают с линиями тока. Свойство ли-
ний тока: они не пересекаются между собой (иначе получилось бы, что в точке их пересечения частица жидкости имеет два направления движения). Значит,
жидкость не проникает сквозь поверхность, образованную линиями тока.
Трубка тока - объём жидкости, ограниченный линиями тока.
Рассмотрим такую трубку тока идеальной жидкости, в произвольном по-
перечном сечении которой скорость частиц жидкости одинакова. Выберем два любых сечения такой трубки тока: S1 , характеризуемое скоростью 1, и
S2 , характеризуемое 2 . Так как идеальная жидкость несжимаема, а её поток неразрывен и не проходит через боковую поверхность трубки, то за время t
через оба сечения пройдут одинаковые объёмы V жидкости:
V1 V2 S1 1 t = S2 2 t , т.е. |
S1 1 = S2 2 |
. |
( ) |
|
|
|
|
Выражение ( ) называют уравнением неразрывности струи; оно хорошо применимо и для реальных каналов с вязкой жидкостью.
Вывод: при сужении канала скорость течения жидкости в нём увеличи-
вается, при расширении - уменьшается.
50
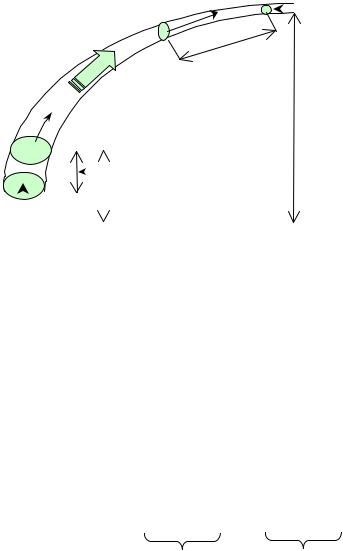
III. Уравнение Бернулли (1738 г., Швейцария)
Как и уравнение неразрывности, оно получено для идеальной жидкости,
т.е. абсолютно несжимаемой жидкости, между молекулами которой нет сил притяжения. Выделим в ламинарном потоке жидкости наклонную трубку то-
ка, а в ней область, ограниченную сечениями S1 и S2. Определим изменение механической энергии W , происходящее в этой области за t . За это время
|
|
|
|
|
|
|
|
|
|
|
|
S2' |
|
F2 |
в выделенную область |
втекает |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
масса жидкости, ограниченная се- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
S2 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
t |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чениями S1 S' и вытекает - |
S |
S' . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
1 |
|
|
|
h2 |
|
|
|
W (Wk Wп)2 (Wk Wп)1. |
|
|
||||||||||||
|
|
|
|
S1' |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
В силу |
непроницаемости для |
|||||||||||
|
|
|
|
|
|
|
|
|
1 t |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жидкости |
стенок |
трубки |
тока, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
h1 |
|
|
|
|
|
|
|
|
|||||||||
F |
S1 |
|
|
|
|
|
|
|
|
имеем m1 |
m2 = m. Тогда мож- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но записать: |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
m 2 |
|
|
|
|
|
m 2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
W= |
|
2 |
+ m g h |
1 |
- m g h . |
|
|
( ) |
|||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Но, согласно закону сохранения энергии, W равно работе А внешних |
|||||||||||||||||||||||
сил (давления) F1 |
и F2 |
по перемещению массы жидкости m внутри выде- |
||||||||||||||||||||||
ленного объёма: |
А = А1 + А2, где |
А1 = F1 1 t , А2 |
= F2 |
2 t |
(знак ‘-‘ |
|||||||||||||||||||
учитывает тот факт, что сила |
F2 |
направлена навстречу потоку жидкости). |
||
Учитывая, что |
F p S (где р - давление), получим : |
|
||
A |
p1 S1 1 t - p2 |
S2 |
2 t = p1 V p2 V , |
( ) |
|
V |
|
V |
|
Приравнивая ( ) и ( ), получим:
m 2 |
|
|
m 2 |
|
||
2 |
+ m g h + p V = |
|
1 |
+ m g h + p V . |
||
|
|
|
||||
2 |
2 |
2 |
2 |
1 |
1 |
|
|
|
|
|
|
||
51

Разделим обе части последнего уравнения на V и учтём, что |
m |
. |
|||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|||
Тогда получим: |
2 |
+ g h |
+ p = |
2 |
+ g h + p . |
|
|
|
|
||||||||
|
2 |
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
2 |
2 |
2 |
|
1 |
1 |
|
плотность |
||||||
Так как сечения S1 |
и S2 |
были выбраны произвольно, то: |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение Бернулли |
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
+ g h+ р = const |
|
|
|
|
|
( ) |
|||||
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Офизическом смысле слагаемых, входящих в уравнение Бернулли:
2 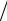 2 - кинетическая энергия единицы объёма жидкости;
2 - кинетическая энергия единицы объёма жидкости;
g h - потенциальная энергия единицы объёма жидкости в гравитационном
поле планеты (Земли);
р - потенциальная энергия единицы объёма жидкости, обусловленная силами внешнего давления.
С другой стороны, так как единицы измерения всех слагаемых уравнения Бернулли - Па(скаль), то эти слагаемые можно рассматривать как давления:
2  2 - динамическое, g h- гидравлическое, р - статическое.
2 - динамическое, g h- гидравлическое, р - статическое.
Вывод (из уравнения Бернулли): в установившемся потоке жидкости полное давление одинаково в любом поперечном сечении потока.
Замечание: несмотря на то, что уравнения Бернулли и неразрывности струи получены для идеальной жидкости, они хорошо применимы не только к реаль-
ным жидкостям, но и к газам (правда, при дозвуковых скоростях 340 м/с).
Частные случаи применения уравнения Бернулли
1) Горизонтальная труба переменного сечения (h1=h2, S1 S2). В этом случае
уравнение Бернулли принимает вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
1 |
p = |
2 |
p |
|
. |
|
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
2 |
1 |
2 |
|
|
|||||
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
S2 |
|
|
|
|
|
|
||||||
52
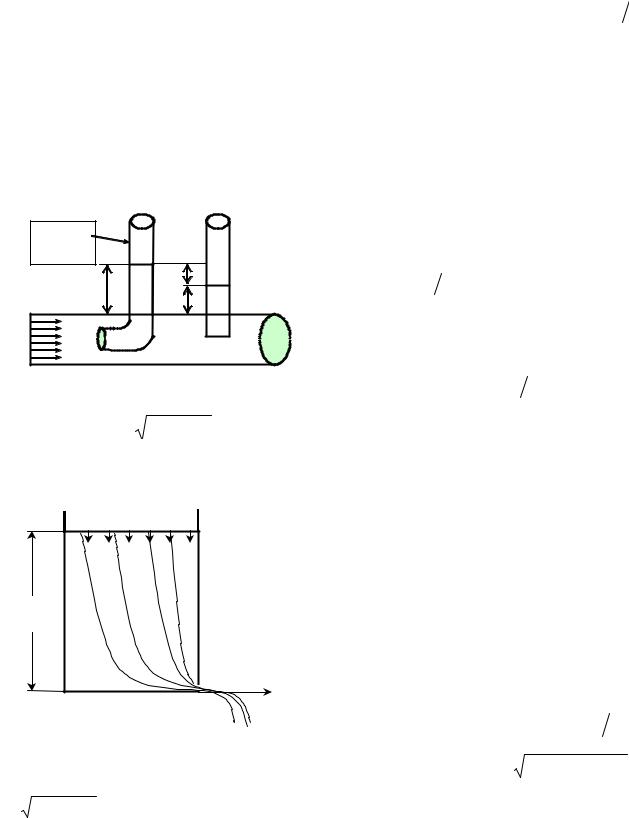
Так как модуль скорости зависит от площади поперечного сечения S, |
то |
||||||||
величину S можно выбрать столь малой, что динамическое давление 2 |
2 |
||||||||
значительно возрастёт, а статическое давление р станет меньше атмосферного |
|||||||||
ро, и такая труба начнёт всасывать воздух, т.е. в сужениях (где скорость увели- |
|||||||||
чивается) горизонтального канала статическое давление понижается. На этом |
|||||||||
принципе работают водоструйные насосы, ингаляторы, пульверизаторы. |
|
||||||||
2) Измерение скорости жидкости трубкой Пито. |
Давления на входных |
||||||||
Трубка |
|
|
|
отверстиях прямой и изогнутой трубок |
|||||
|
|
|
отличаются на величину динамического |
||||||
П и т о |
|
|
|
||||||
h2 |
|
h |
|
давления 2 2 , |
которое уравновеши- |
||||
|
h1 |
|
|||||||
|
|
|
вается |
дополнительным |
гидростатиче- |
||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ским давлением более высокого столба |
|||||
|
|
|
|
||||||
жидкости |
р g h . |
Из равенства этих давлений ( 2 |
2 = g h ) |
||||||
получим: = |
2 g h . |
|
|
|
|
|
|
|
|
3) Истечение жидкости из отверстия. Формула Торричелли. |
|
|
|||||||
|
S |
|
|
Так как S1>> S2 , то, |
в силу уравнения |
||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
неразрывности струи, |
1 << 2 и можно |
||||
|
|
|
положить 1 0. Кроме того, учтём, что |
||||||
h |
|
|
|
||||||
|
|
|
внешнее давление (атмосферное давле- |
||||||
|
|
S2 |
2 |
ние) на |
уровнях 1 и 2 практически оди- |
||||
|
|
наковое, т. е. p1 p2 . Тогда из уравнения |
|||||||
|
|
|
|
||||||
|
|
|
|
Бернулли имеем: |
g h |
= 2 2 |
+ |
||
|
|
|
|
|
|
|
1 |
|
|
g h2 , |
откуда получаем формулу Торричелли: |
2 |
2 g (h1 h2 ) = |
||||||
2 g h , |
согласно которой скорость вытекающей струи равна скорости |
||||||||
свободно падающего с высоты h тела. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
53 |
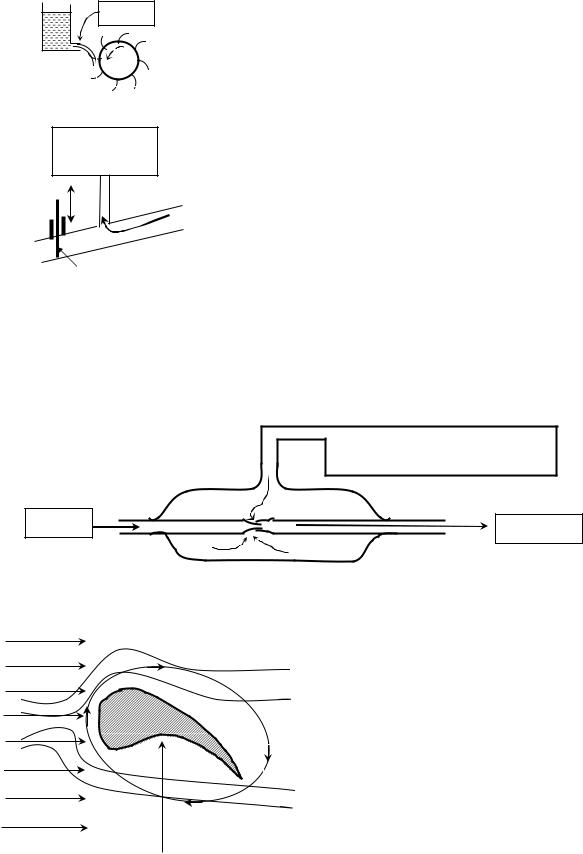
Некоторые приложения уравнения Бернулли |
||
1. Гидротурбина. Потенциальная энергия воды (водохранилища) перехо- |
||
Сопло |
дит в сoпле в кинетическую энергию струи, приводя- |
|
|
щую во вращение турбину и сопряжённый с ней ротор |
|
электрогенератора. |
||
|
||
2. Гидротаран. При опускании заслонки динамическое давление падает до |
||
Резервуар |
нуля, поэтому статическое давление резко возрастает, |
|
перегоняя часть жидкости, текущей по трубе, в распо- |
||
|
||
|
ложенный наверху резервуар. Таким образом, работа |
|
|
совершается за счёт поставщика жидкости. |
|
Подвижная |
Примеры (гашения) гидротарана: 1) в водопроводах |
|
заслонка |
винтовые краны (а не поворотные, как у самовара); |
|
|
||
2) изгибы трубопроводов (для уменьшения кинетической энергии перегоняе- |
||
мой по ним жидкости). |
||
3. Водоструйный насос. Создаёт разрежение в откачиваемом сосуде до 90 Па. |
||
Откачиваемый резервуар с газом
Вода |
Вода + газ |
4. Подъёмная сила крыла самолёта. В 1904 году русским инженером Н.Е.Жу-
о |
ковским был предложен изображён- |
о цирк |
ный на рисунке профиль поперечно- |
|
го сечения крыла самолёта. При та- |
|
ком профиле крыла вокруг него воз- |
|
никает циркулирующий воздушный |
|
цирк |
|
поток. В результате, над крылом ско- |
о цирк |
рость надвигающегося на самолёт |
Fподъём. |
|
54
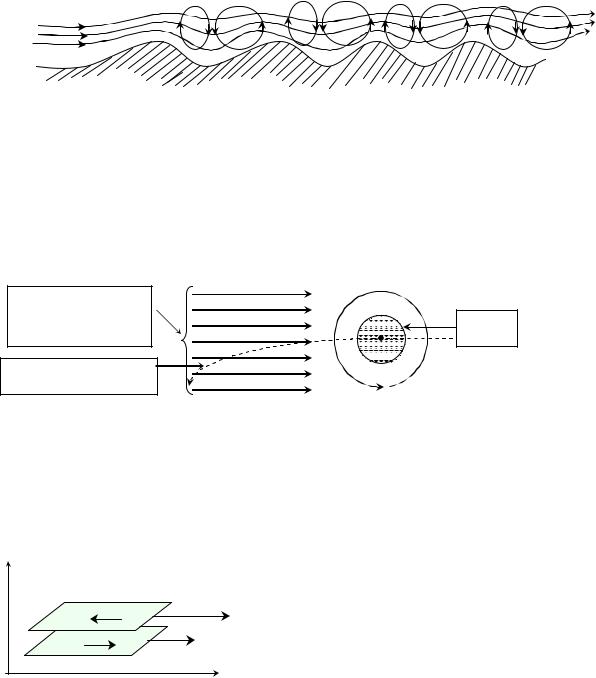
воздушного потока складывается со скоростью циркуляции, а под крылом -
вычитается. Различие скоростей воздушной струи под и над крылом порож-
дает разность статических давлений, направленную снизу вверх и создаю-
щую подъёмную силу Fподъём. .
5. Аэрация почвы после вспашки (сопровождается обогащением почвы кислородом). Воздушные горизонтальные потоки над неровной поверхно-
стью земли образуют трубки тока переменного сечения, что приводит к пе-
репадам статического давления и образованию вертикальных вихрей.
6. "Кручёный мяч" в футболе (эффект Магнуса). Удар по мячу наносят в точку, смещённую от его центра, в результате мяч приобретает не только по-
ступательное, но и вращательное движение. Слои воздуха, прилегающие к мя-
чу, увлекаются им. Поэтому справа от мяча результирующая скорость воздуха меньше, чем о , а слева – больше; статическое же давление, в соответствии с уравнением Бернулли, наоборот, справа от мяча больше, а слева – меньше.
Надвигающийся |
|
|
о |
о цирк |
|
|
|
|
|||
воздушный поток |
|
Удар |
|||
|
|
|
|
||
Траектория полёта |
|
|
о цирк |
||
|
|
|
|
||
|
IV. Течение вязкой жидкости |
||||
Вязкость ( ) - это свойство реальных жидкостей оказывать сопротивле- |
|||||
ние перемещению одной части жидкости относительно другой. Вязкость яв- |
|||||
ляется результатом притяжения молекул жидкости и их переходов из одного |
|||||
z |
|
|
слоя в другой. При перемещении одних слоёв |
||
Fтр |
S |
2 |
реальной жидкости относительно других воз- |
||
|
никают силы |
внутреннего трения, направ- |
|||
S |
|
|
|||
1 |
х |
ленные по касательной к поверхности слоёв. |
|||
F |
|||||
тр |
|
|
|
|
|
|
|
|
|
55 |
|
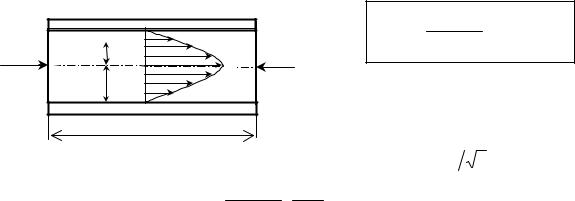
Сила внутреннего трения между слоями жидкости выражается эмпирической
|
|
|
d |
|
|
|
формулой Ньютона: |
F |
|
S , где коэффициент |
, зависящий от |
||
|
||||||
|
тр |
dz |
|
|
||
|
|
|
|
|
||
природы жидкости, называется динамической вязкостью (или просто вязко-
стью).
Единица измерения вязкости в СИ - Паскаль-секунда (Па с), в СГС [ ] =
1 П(уаз); причём 1 П = 0,1 Па с. Для жидкостей ~ T 1 . Например, для во-
ды (0o ) 1,8 10 3 Па с, а (90o ) 3,2 10-4 Па с. Особенно сильно вязкость зависит от температуры для масел.
|
|
|
Формула Пуазейля |
|
|
||
Это также эмпирическая формула, описывающая распределение скорости |
|||||||
вязкой жидкости по поперечному сечению трубы при ламинарном течении: |
|||||||
|
|
|
|
|
(r) p1 p2 (R2 r2 ) |
|
|
p1 |
r |
|
|
p2 |
4 l |
, |
|
|
R |
|
|
|
где r – расстояние от оси трубы до |
||
|
|
|
|
|
|||
|
l |
|
|
|
данной (произвольной) точки сечения. |
||
Откуда средняя скорость потока, достигаемая при r =R |
2 , может быть рас- |
||||||
считана по формуле: |
|
p p |
2 |
R2 |
|
|
|
1 |
. |
|
|
||||
|
|
ср |
l |
8 |
|
|
|
|
|
|
|
|
|||
Тогда объём жидкости V, протекающей через круглое поперечное сечение |
|||||||
S за t 1с, равен: |
V S ср t |
p p |
2 |
|
R4 |
|
p |
|
|
|||||
|
|
|
1 |
|
|
|
|
|
, |
|
||||
|
|
|
|
l |
|
8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
8 l |
|
|
|
|
|
|
|
|
|
||||
где = |
- гидравлическое сопротивление канала (~ R 4 ). |
|
||||||||||||
R4 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная R, l, задавая р=(р1-р2) и измеряя V, Пуазейль определял |
. |
|||||||||||||
Характер течения (ламинарный или турбулентный) определяют, оценив |
||||||||||||||
значение |
безразмерной величины Re, |
называемой |
числом |
Рейнольдса: |
||||||||||
56
Re |
ср d |
|
ср d |
, где |
- кинематическая вязкость, d - диаметр |
|
|
||||
|
|
|
|
||
трубы. При Re 1000 течение считают ламинарным, при 1000 Re 2000 го-
ворят о переходе от ламинарного к турбулентному течению, а при Re 2300
течение - турбулентное.
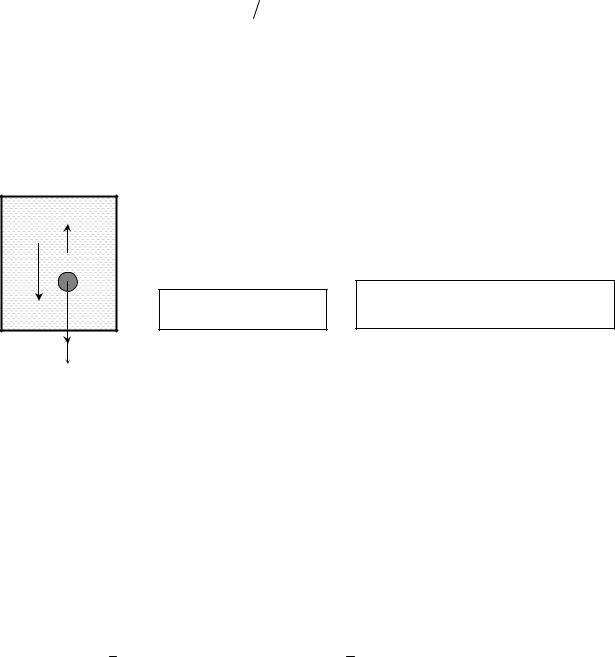
Определение динамической вязкости по методу Стокса
FA
 Fc
Fc
Fт
Сила сопротивления равномерному движению тела сферической формы в реальной жидкости описывается эмпирической формулой Стокса и носит его имя:
Справедлива только при ламинар- Fc 6 r  ном обтекании тела жидкостью.
ном обтекании тела жидкостью.
y |
Сила Стокса Fc всегда направлена в сторону прo- |
тивоположную направлению скорости движения тела. |
|
При равномерном погружении, а оно неизбежно наступает, так как Fc ~ ,
имеем a =0. Тогда, уравнение движения тела (в проекции на ось у) имеет вид:
F F |
F |
0, где F |
m |
м |
g V |
м |
g |
4 |
r3 |
м |
g |
- сила тяжести, |
м |
- |
|||||||||
3 |
|||||||||||||||||||||||
т |
c |
А |
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
плотность материала шарика, F |
m |
|
g V |
ж |
g |
4 |
r3 |
ж |
g - (вытал- |
||||||||||||||
|
3 |
||||||||||||||||||||||
|
|
|
|
|
|
А |
|
ж |
|
|
|
|
|
|
|
|
|
|
|||||
кивающая) сила Архимеда, ж - плотность жидкости. Подставив выражения для всех сил (с учётом их направления), получим:
43 r3 м g - 6 r - 43 r3 ж g = 0.
Откуда имеем: |
|
2 r2 |
g ( |
м |
|
ж |
) |
|
. |
|
9 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
V. Меандры рек
Меандрами называют периодические изгибы равнинных рек. Происхож-
дение этого термина связано с древнегреческим названием «Меандр» извест-
ной своими изгибами реки в Малой Азии. Почему же русло реки даже на равнине с однородной почвой изгибается? Ответ на этот вопрос впервые был дан А. Эйнштейном в докладе Причина образования извилин в руслах рек и
57
так называемый закон Бэра , представленном Прусской академии наук в 1926 |
||||||||
году. При этом Эйнштейн использовал наглядную аналогию движения вра- |
||||||||
щающейся воды в стакане чая и в русле рек. Последуем примеру Эйнштейна. |
||||||||
|
|
|
Движение чаинок в стакане |
|
|
|
||
|
Как ведут себя чаинки при размешивании сахара в стакане? Пока ложечка |
|||||||
движется, они следуют за ней. Когда же ложечка изымается из стакана, то |
||||||||
вода постепенно останавливается, а чаинки собираются в центре дна стакана. |
||||||||
Почему? Чтобы ответить на этот вопрос, выясним сначала, какую форму |
||||||||
принимает свободная поверхность воды, вращающейся в стакане. |
|
|
||||||
|
Из опыта известно, что поверхность воды при этом искривляется, прини- |
|||||||
мая форму параболоида. Покажем необходимость искривления свободной |
||||||||
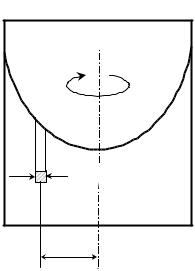
поверхности вращающейся воды. Для вращения частичек воды в стакане, не- |
||||||||
|
|
|
обходимо, чтобы равнодействующая всех сил, |
|||||
|
|
|
действующих на |
каждую частичку, создавала |
||||
|
|
|
центростремительное ускорение. Выделим мыс- |
|||||
|
|
|
||||||
|
|
|
ленно внутри жидкости на расстоянии r от оси |
|||||
h1 |
h2 |
вращения кубик массой m. При равномерном |
||||||
|
вращении кубик испытывает центростремитель- |
|||||||
|
|
F2 |
||||||
|
ное ускорение 2 r, создаваемое разностью сил |
|||||||
F1 |
|
|
||||||
|
|
r |
гидравлического давления, действующего на его |
|||||
|
|
боковые |
грани. |
Следовательно: |
m 2 r |
= |
||
|
|
|
||||||
F1 F2 |
( p1 |
p2 ) S , где S - площадь боковой грани кубика. |
|
|
|
|||
|
Но давления p1 g h1 и p2 g h2 определяются расстояниями h1 |
и h2 |
||||||
до свободной поверхности жидкости, поэтому: m 2 r = g S (h |
h ). |
|||||||
|
|
|
|
|
|
1 |
|
2 |
Поскольку левая часть последнего уравнения больше нуля, то, следова- |
||||||||
тельно: h1> h2 . То есть свободная поверхность жидкости не горизонтальна и, |
||||||||
чем больше угловая скорость , тем сильнее искривление поверхности. |
|
|
||||||
58 |
|
|
|
|
|
|
|
|
