
Курс лекций по высшей математике. 2 часть
.pdf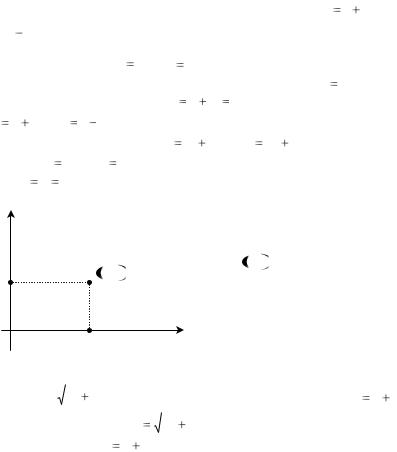
ГЛАВА I
НЕКОТОРЫЕ СВЕДЕНИЯ О КОМПЛЕКСНЫХ ЧИСЛАХ И МНОГОЧЛЕНАХ
§1. Комплексные числа
1. Понятие комплексного числа
Комплексным числом z называется число вида z x iy , где
i2  1 , а x и y–вещественные числа. Число x называется действительной частью, y–мнимой частью комплексного числа z. Это записывают
1 , а x и y–вещественные числа. Число x называется действительной частью, y–мнимой частью комплексного числа z. Это записывают
следующим образом: |
x |
Re z, y |
Im z . |
|
|
|
|
|
|||||||||||
Если x=0, то число z называют чисто мнимым; если y 0 , то полу- |
|||||||||||||||||||
чается |
вещественное |
число |
z |
x |
0i |
x . Два |
комплексных |
числа |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z x |
iy и z |
x |
iy |
называются сопряженными. |
|
|
|
||||||||||||
Два комплексных числа |
z1 |
x1 |
iy1 |
и z2 |
x2 |
iy2 |
равны друг дру- |
||||||||||||
гу, если x1 |
|
x2 |
|
и |
y1 |
y2 ; комплексное число z считается равным нулю, |
|||||||||||||
если x |
y |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всякое |
комплексное |
число |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
можно изобразить на плоскости, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.к. каждому z соответствует упо- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рядоченная |
пара |
вещественных |
|||
y |
|
|
|
|
M x, y |
|
|
|
чисел x,y |
: |
|
|
|
||||||
|
|
|
|
|
|
|
|
Число z=0 ставится в соот- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ветствие |
началу |
координатной |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости. Такую плоскость мы в |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дальнейшем будем называть ком- |
|||||
0 |
|
|
|
|
|
x |
|
|
|
|
x |
|
плексной плоскостью, ось абс- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цисс–действительной, а ось орди- |
|||||
нат–мнимой осью комплексной плоскости. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Число |
|
|
x2 |
|
|
y2 |
называется модулем комплексного числа z |
x iy |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и обозначается |
|
z |
|
или r:r |
x2 |
y2 . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||||
Отметим, что |
z |
|
x iy |
называют алгебраической формой записи |
|||||||||||||||
комплексного числа. |
|
|
|
|
|
|
|
|
|
|
|||||||||
3

2. Тригонометрическая и показательная формы комплексного числа
Для определения положения точки на плоскости можно пользоваться полярными координатами r, , где r–расстояние точки от нача-
, где r–расстояние точки от нача-
ла координат, а φ–угол, который составляет радиус–вектор этой точки с положительным направлением оси Ox. Положительным направлением изменения угла φ считается направление против часовой стрелки. Вос-
пользовавшись |
связью |
декартовых |
и |
полярных |
координат: |
||||||||||||
x |
r cos , y |
r sin |
, получим тригонометрическую форму |
записи |
|||||||||||||
комплексного числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
z r sin |
|
i sin |
|
|
(1) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
где |
r |
x2 |
y2 |
, φ–аргумент комплексного числа, который нахо- |
||||||||||||
дят |
из |
формул |
cos |
|
x |
, |
sin |
|
y |
или |
в |
силу того, |
что tg |
|
y |
, |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
x |
||
arctg xy . Заметим, что при выборе значений φ из последнего урав-
нения необходимо учитывать знаки x и y.
Пример1. Записать в тригонометрической форме комплексное чис-
ло z |
1 |
|
|
|
i 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Решение. |
Найдем модуль |
|
и |
|
аргумент |
комплексного |
|
числа: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 . |
Угол φ найдем из соотношений |
cos |
|
x |
, |
sin |
|
|
|
y |
. |
|||||||||||||||
|
z |
|
|
1 |
3 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Тогда получим cos |
|
, sin |
|
. Очевидно точка |
z |
1 |
i |
|
3 на- |
||||||||||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ходится во второй четверти: |
120o |
2 |
3 |
π . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя |
в |
формулу |
(1) |
|
найденные r |
и |
φ, |
|
имеем |
||||||||||||||||||||||
|
z |
2 cos |
2 |
i sin |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Замечание. Аргумент комплексного числа определен неоднознач- |
|||||||||||||||||||||||||||||||
но, а с точностью до слагаемого, кратного 2π. Тогда через |
arg z обо- |
||||||||||||||||||||||||||||||||||
значают |
|
|
|
значение |
|
аргумента, |
|
заключенное |
в |
пределах |
|||||||||||||||||||||||||
|
o |
|
arg z |
2π |
o . Тогда Argz |
arg z |
2kπ . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
Используя известную формулу Эйлера |
ei |
cos |
i sin |
, |
получа- |
||||||||||||||||||||||||||
ем показательную форму записи комплексного числа. Имеем |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
r cos |
|
|
|
i sin |
|
rei |
|
|
|
|
|
|
|
|
|
|
|
|||
4

3. Действия над комплексными числами
|
|
1.Сумма двух комплексных чисел |
z1 |
|
x1 |
|
iy1 и |
|
z2 |
x2 |
|
iy2 |
опре- |
|
|||||||||||||||||||||||||||||||||||||||||||||||
деляется согласно формуле z1 |
|
|
|
|
|
z2 |
|
|
|
|
x1 |
x2 |
i y1 |
y2 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
2.Операция вычитания комплексных чисел определяется как опе- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рация, |
|
|
|
обратная |
|
сложению. |
|
|
|
|
|
Комплексное |
|
|
число |
|
|
z |
z1 |
|
z2 , |
|
если |
|
|||||||||||||||||||||||||||||||||||||
z2 |
|
z |
|
|
|
z1 , |
|
является |
разностью |
|
комплексных |
чисел z1 и |
z2. |
Тогда |
|
||||||||||||||||||||||||||||||||||||||||||||||
z |
|
x1 |
|
|
|
x2 |
|
i y1 |
|
y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3.Произведение двух комплексных чисел z1 |
x1 |
|
|
iy1 |
и z2 |
x2 |
iy2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
определяется по формуле |
z1z2 |
|
|
|
x1 |
|
iy1 |
x2 |
|
iy2 |
x1x2 |
iy1x2 |
ix1 y2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
i 2 y y |
2 |
|
|
x x |
2 |
|
|
y y |
2 |
|
i x y |
2 |
|
|
|
x |
2 |
y |
|
.В частности z |
z |
|
x |
iy |
x |
|
iy |
|
|
||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= x 2 |
|
|
y 2 . Можно получить формулы умножения комплексных чисел в |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
показательной |
|
|
|
|
|
и |
|
|
|
тригонометрической |
|
формах. |
|
Имеем |
|
||||||||||||||||||||||||||||||||||||||||||||||
z z |
2 |
|
|
r ei |
1 |
|
r ei 2 |
|
|
r r ei |
1 |
|
|
|
2 |
|
|
|
|
|
|
r r |
|
cos |
1 |
|
|
|
2 |
|
i sin |
|
1 |
2 |
. |
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
4.Деление комплексных чисел определяется как операция, обратная |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
умножению, то есть число |
|
|
z |
|
|
|
|
|
z1 |
|
|
|
называется частным от деления z1 на |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
z2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z2, если z1 |
|
|
z2 |
|
|
z . Тогда |
|
z1 |
|
|
|
|
|
x1 |
|
|
iy1 |
|
x1 |
iy1 x2 |
iy2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
z2 |
|
|
|
|
|
x2 |
|
|
iy2 |
x2 |
iy2 x2 |
iy2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
x x |
2 |
|
|
iy x |
2 |
|
|
ix y |
2 |
|
|
|
|
i 2 y y |
2 |
|
|
|
|
x x |
2 |
|
y y |
2 |
i x y |
2 |
x |
y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
2 |
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2 |
|
y2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2 |
y2 2 |
|
|
|
|
|||||||||||||
Окончательно |
|
|
z1 |
|
|
|
|
x1x2 |
|
|
y1 y2 |
|
|
i |
|
|
|
x1 y2 |
|
|
x2 y1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
x |
2 |
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
B показательной и тригонометрической формах: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
z1 |
|
|
|
r1ei |
1 |
|
|
|
|
r1 |
ei |
1 |
2 |
|
|
|
|
|
r1 |
|
cos |
|
|
|
|
|
|
|
|
i sin |
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
r ei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
1 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
z |
|
|
|
|
2 |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
5.Возведение в целую положительную степень комплексного числа |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
лучше производить, если число записано в показательной или тригоно- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
метрической формах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Действительно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
|
|
|
|
|
|
|
|
|
|
z |
rei |
, то |
|
|||||||||||||||||||||||
zn |
|
|
rei |
n |
|
r nein |
|
|
|
r n |
cos n |
|
|
|
|
|
i sin n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Формула z n |
|
|
r n cos n |
|
|
|
|
|
|
i sin n |
|
|
|
называется формулой Муавра. |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
6.Извлечение корня n–й степени из комплексного числа определя- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ется как операция, обратная возведению в степень n, |
|
n |
1,2,3,... то есть |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5

|
|
|
|
|
|
|
|
|
||||||
комплексное число |
z |
|
n z |
называется корнем n–й степени из ком- |
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
плексного |
числа z, |
если |
|
z |
z n . Из |
этого определения следует, что |
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
r r n , a |
|
|
|
|
|
|
|
|
|
|||||
r |
n r . |
n |
1 |
, a |
1 |
n , что следует из формулы Муавра, |
||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
записанной для числа z :z r n cos n |
1 |
i sinn |
1 |
. |
||||||||||
|
|
|
|
|
|
1 |
1 |
|
|
|
||||
Как было отмечено выше, аргумент комплексного числа определен |
||||||||||||||
неоднозначно, а с точностью до слагаемого, кратного 2π. Поэтому
Argz |
2πk , а аргумент числа z1, зависящий от k, обозначим φk и бу- |
|||||
дем вычислять по формуле |
|
|
|
2πk |
. Ясно, что существует n ком- |
|
k |
|
|
||||
|
|
n |
|
n |
||
|
|
|
|
|||
плексных чисел, n–я степень которых равна числу z. Эти числа имеют
один и тот же модуль, равный n  r , а аргументы этих чисел получаются при k 0, 1, ..., n 1. Таким образом, в тригонометрической форме корень n–й степени вычисляют по формуле:
r , а аргументы этих чисел получаются при k 0, 1, ..., n 1. Таким образом, в тригонометрической форме корень n–й степени вычисляют по формуле:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kπ |
|
|
|
|
|
|
|
|
|
|
|
|
2kπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
n z |
n r |
|
cos |
|
|
|
|
|
i sin |
, |
|
k |
0, 1, ..., n 1, |
а |
в |
показа- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
2kπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тельной–по формуле |
|
z |
|
|
|
|
re |
|
n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Пример 2. Возвести число z |
3 |
|
|
|
i |
в пятую степень. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Получим тригонометрическую форму записи числа z. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
||||||
r |
3 1 |
|
|
2, cos |
|
|
|
|
|
, sin |
|
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
, |
|
|
|
а |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z |
2 cos |
|
π |
|
|
i sin |
|
|
|
|
π |
|
|
|
|
|
. Тогда |
|
|
по |
формуле |
|
|
Муавра |
|
получим: |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
6 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
z5 |
2 cos |
5 |
|
|
|
|
i sin |
|
|
5 |
|
|
|
|
|
|
|
2 cos |
|
5 |
|
|
|
|
i sin |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
cos |
i sin |
|
|
|
2 |
|
|
|
|
|
|
|
i |
|
|
|
2 |
|
|
|
i |
|
|
3 |
|
|
i |
|
|
z . |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. Найти все значения |
1 |
|
|
i |
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. r=2, а φ найдем из уравнений cos |
|
|
1 |
,sin |
|
|
|
|
|
3 |
|
. Эта |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точка 1 i |
3 |
|
|
|
|
находится в четвертой четверти, то есть |
|
|
|
. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6

r |
2 cos |
|
|
π |
|
i sin |
|
π |
, |
значения |
корня |
|
|
находим из |
выражения |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
2kπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
2kπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
i |
3 |
|
|
|
|
|
|
2 |
cos |
|
|
|
|
|
|
|
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
При k |
|
|
|
|
0 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
i sin |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
i |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
z0 |
2 |
|
|
cos |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
При k |
|
|
|
1 имеем еще одно значение корня |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
z1 |
2 |
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
cos |
|
π |
|
i sin |
|
π |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
cos |
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
i sin |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Можно найти значения корня из числа z, представив число в пока- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iπ |
3 |
2kπ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
2e i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
зательной форме. Т.к. r=2, a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
то z |
|
|
3 |
|
, a |
|
z |
|
2e |
2 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e i |
|
|
|
|
|
|
|
|
|
|
cos |
π |
|
|
|
i sin |
π |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
i |
|
. При k=1 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Тогда при k=0 имеем |
|
z |
o |
|
|
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei |
π |
3 |
|
2π |
|
|
|
|
|
|
ei |
5 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
имеем z |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
6 |
|
|
|
|
|
|
|
2 |
cos |
π i sin |
π |
|
|
2 |
|
|
|
cos |
|
|
|
|
|
i sin |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
i |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§2. Некоторые сведения о многочленах |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Разложение многочлена на множители |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Функция |
P |
x |
|
|
|
|
A xn |
|
|
|
A xn 1 |
... |
|
|
A , |
где n–целое число, называ- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ется многочленом или рациональной целой функцией от x. Число n называют степенью многочлена. Коэффициенты A0, A1, ..., An –это дейст-
7

вительные или комплексные числа. Независимая переменная x также может быть как действительным, так и комплексным числом.
Корнем многочлена называется такое значение переменной x, которое обращает многочлен в нуль.
Теорема Безу. Число a является корнем многочлена Pn x тогда и
только тогда, когда многочлен делится на x–a без остатка. Доказательство. Если многочлен степени n разделить на x–a, то
очевидно в частном получится многочлен степени n 1 , а в остатке от деления число, то есть
Pn x |
x a Qn 1 x r |
(2) |
Тогда если x=a–корень многочлена Pn x , то Pn a |
0 и, подстав- |
|
ляя x=a, в обе части равенства (2), получим r=0.
Обратно, если r=0, то при x=a правая часть (2) обращается в нуль,
тогда и Pn a |
0 , то есть x=a–корень Pn x . |
|
|
|
|||||||||
Из теоремы Безу следует, что если x=a–корень многочлена, то |
|||||||||||||
Pn x |
x |
a Qn 1 x |
|
|
|
|
|
|
|
|
(3) |
|
|
Например, многочлен P |
x |
|
x3 |
6x2 |
11x |
6 при x=1 обращается |
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
в нуль, тогда он делится на x–1. Разделим многочлен на x–1: |
|||||||||||||
|
|
|
_ x3 |
6x2 |
11x 6 |
|
x 1 |
|
|
||||
|
|
|
|
x3 |
x2 |
|
|
|
|
x2 |
5x |
6 |
|
|
|
|
|
_ |
5x2 |
11x |
6 |
|
|
|
|
||
|
|
|
|
|
|
5x2 |
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
_ 6x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
6x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Таким образом, |
x3 6x2 |
11x |
6 |
x |
1 x2 |
5x |
6 . |
||||||
Теорема (доказывается в курсе алгебры). Всякий многочлен Pn x |
|||||||||||||
степени n |
1 имеет по крайней мере один корень. |
|
|
||||||||||
Теорема. Всякий многочлен степени n разлагается на n линейных |
|||||||||||||
множителей вида x |
a и множитель, равный коэффициенту при xn . |
||||||||||||
Доказательство. Пусть |
P |
x |
A xn |
A xn |
... |
A |
. Он имеет по |
||||||
|
|
|
|
n |
|
|
0 |
|
1 |
|
|
n |
|
крайней мере один корень. Пусть это будет a1. Тогда на основании теоремы Безу Pn x  x a1 Qn 1 x , где Qn 1 x –многочлен степени n 1 .
x a1 Qn 1 x , где Qn 1 x –многочлен степени n 1 .
Он тоже имеет по крайней мере один корень. Обозначим его a2 . Тогда
Qn 1 x  x a2 Qn 2 x , где Qn 2 x –многочлен степени n 2 . Продолжая этот процесс выделения линейных множителей, дойдем до со-
x a2 Qn 2 x , где Qn 2 x –многочлен степени n 2 . Продолжая этот процесс выделения линейных множителей, дойдем до со-
8

отношения Q1 x x an Q0 x , где Q0 x –многочлен нулевой степени, то есть некоторое фиксированное число. Это число, очевидно, равно коэффициенту A0 при xn многочлена Pn x .
x an Q0 x , где Q0 x –многочлен нулевой степени, то есть некоторое фиксированное число. Это число, очевидно, равно коэффициенту A0 при xn многочлена Pn x .
Подставляя в формулу (3) выражения для Qn 1 x , Qn 2 x , ..., Qo , получим
Pn x A0 x a1 x a2 ... x an
Замечание. Числа a1, a2, ..., an –корни многочлена Pn x подстановке этих чисел в формулу (4) получаем в правой части формулы нуль, это и означает, что Pn a1 Pn a2 ... Pn an 0 .
Никакое значение x a , отличное от a1, a2, ..., an не может быть корнем многочлена Pn x , т.к. ни один из множителей в правой части
(4) не обращается в нуль. Отсюда вытекает, что многочлен n–й степени не может иметь больше чем n различных корней.
2. О кратных и комплексных корнях многочлена
Если в разложении многочлена Pn x на множители (4) некоторые
на множители (4) некоторые
линейные множители окажутся одинаковыми, то их можно объединить, и тогда разложение многочлена на множители будет иметь вид:
|
|
P x |
A |
x |
a |
k1 x |
a k2 |
... x |
a |
km |
(5) |
|
|
n |
o |
|
1 |
|
2 |
|
m |
|
|
|
При этом k1 |
k2 ... |
km |
n . В этом случае корни a1, a2, ..., am на- |
|||||||
зываются корнями кратности k1, k2 , ..., km соответственно. |
|
||||||||||
|
Например, многочлен |
P x |
x3 |
5x2 |
8x |
4 |
x 2 x |
2 x 1 |
|||
x |
2 2 x 1 . |
Корень |
a |
|
2 –двукратный корень этого многочлена, |
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
a2 |
1 –простой корень. |
|
|
|
|
|
|
|
|
|
|
|
Имеет место теорема: всякий многочлен n–ой степени имеет ровно |
||||||||||
n корней (действительных или комплексных). |
|
|
|
||||||||
|
Теорема (без доказательства). Если многочлен с действительными |
||||||||||
коэффициентами имеет комплексный корень a |
bi , то он имеет и со- |
||||||||||
пряженный корень a bi . |
|
|
|
|
|
|
|
|
|||
Итак, в разложении (4) многочлена на множители комплексные корни входят попарно сопряженными. Перемножив линейные множители x  a bi и x
a bi и x  a bi , соответствующие паре комплексно сопря-
a bi , соответствующие паре комплексно сопря-
женных корней, получим квадратный трехчлен с действительными ко-
эффициентами: x |
a |
bi x |
a bi |
x a bi x a bi |
x a 2 |
b2 x2 2ax a2 b2 x2 px q, |
|
где p 2a, q |
a2 |
b2 –действительные числа. |
|
|
|
|
9 |

Если корень a bi является корнем кратности k, то сопряженный корень a bi имеет ту же кратность k. Это означает, что в разложении
многочлена на множители наряду с множителями |
x |
a bi |
k входят |
||||||||||
множители |
x |
a |
bi |
k , то есть множители |
x2 |
px |
q k . |
|
|||||
|
Таким образом, многочлен с действительными коэффициентами |
||||||||||||
разлагается на множители согласно формуле |
|
|
|
|
|
||||||||
P x |
A x |
a |
k1 |
x |
a k2 ... x |
a |
kr x2 |
p x |
q |
1 ... x2 |
p x |
q s , |
|
n |
o |
1 |
|
|
2 |
r |
|
1 |
1 |
|
|
s |
s |
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
k2 ... |
kr |
2e1 |
... 2es |
n |
|
|
(6) |
|
3. Разложение правильных рациональных дробей на простейшие
Рассмотрим рациональную дробь |
P x |
, где |
P x и Q x – |
|
Q x |
||||
|
|
|
многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена P x меньше степени многочлена Q x .
Если рациональная дробь является неправильной, то произведя деление P x на Q x по правилу деления многочленов, ее можно пред-
|
|
|
|
|
P x |
|
|
|
P x |
|
|
|
|
|
|
||
ставить в виде |
|
|
|
R x |
1 |
, где R(x), |
P( x ) –некоторые много- |
||||||||||
Q x |
|
Q x |
|||||||||||||||
|
|
P1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
члены, а |
|
|
–правильная рациональная дробь. |
|
|
||||||||||||
Q x |
|
|
|||||||||||||||
Правильные рациональные дроби вида |
|
|
|
||||||||||||||
|
|
A |
|
|
A |
|
|
Ax |
B |
Ax |
B |
||||||
I. |
|
|
, II. |
|
|
|
|
, III. |
|
|
|
, IV. |
|
|
|
, где k–целое |
|
x |
a |
|
x |
|
a k |
|
x2 |
px q |
|
x2 px |
q k |
||||||
положительное |
|
число |
≥2, |
|
дискриминант |
квадратного трехчлена |
|||||||||||
x2 px |
q отрицателен, называются простейшими дробями I, II, III и |
||||||||||||||||
IV типов.
Правильную рациональную дробь, числитель и знаменатель которой не имеют общих корней, то есть дробь несократимую можно разложить на сумму простейших дробей.
Здесь имеют место три случая.
10

1.Все корни многочлена |
Q x , |
стоящего в знаменателе, действи- |
|||||
тельны и различны, то есть |
Q x |
x a x |
a ... x |
a |
. Тогда |
P x |
|
|
|||||||
|
|
1 |
2 |
n |
Q x |
||
|
|
|
|
|
|
||
можно разложить на n простейших дробей I типа:
|
P x |
|
A1 |
|
A2 |
... |
An |
(7) |
|
Q x |
|
x a1 |
x a2 |
x an |
|||
|
|
|
|
|||||
2.Все корни многочлена Q x |
действительны, но среди них имеют- |
|||||||
ся кратные, то есть Q x x a1 k1 x a2 k2 ... x am km . Тогда рацио-
x a1 k1 x a2 k2 ... x am km . Тогда рацио-
нальную дробь можно разложить на сумму простейших дробей I и II типов:
|
P x |
|
A (1) |
|
A (2) |
|
|
A (k1 ) |
|
|
|
|
A |
(1) |
|
A (2) |
|
|
|
A (km ) |
|
|
|
|
|
1 |
|
1 |
|
... |
1 |
|
|
... |
|
m |
|
m |
|
... |
|
m |
|
(8) |
|
|
Q x |
|
x a1 |
|
x a |
2 |
x a |
k1 |
|
x am |
|
x a |
2 |
|
x a |
km |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
m |
|
|
|
|
|
||
|
3.Среди корней знаменателя правильной рациональной дроби име- |
|||||||||||||||||||||
ются |
комплексно |
|
сопряженные |
|
не |
повторяющиеся, |
то есть |
|||||||||||||||
Q x |
x2 px |
q ... x2 |
x s ... x a |
k1 |
... x a |
k . |
||
|
|
|
|
|
|
1 |
|
2 |
|
Тогда дробь |
|
P x |
|
разлагается на простейшие дроби I, II и III ти- |
|||
|
|
Q x |
||||||
|
|
|
|
|
|
|
||
пов. Запишем ту часть разложения, которая соответствует множителям
|
x2 |
|
px |
q, ... x2 |
x |
|
s знаменателя: |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
P x |
|
|
Ax |
B |
... |
|
|
Mx |
|
N |
... |
(9) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Q x |
|
x2 |
px q |
|
x2 |
x s |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Пример |
4. |
Разложить |
на |
|
простейшие рациональную |
дробь |
|||||||||||||||||||
|
|
x 1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
4x2 |
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Решение. Разложим знаменатель дроби на простейшие множители: |
|||||||||||||||||||||||||
|
|
|
x3 |
4x2 |
3x |
x x2 |
4x |
3 |
|
x x 1 |
x |
3 . Теперь по формуле (7) |
|||||||||||||||
разложим дробь на простейшие дроби I типа: |
|
|
|||||||||||||||||||||||||
|
|
|
|
x 1 |
|
|
|
|
|
|
x |
1 |
|
|
|
A |
B |
|
C |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x3 |
4x2 |
3x x x 1 x 3 |
|
x x 1 x 3 |
|
|
||||||||||||||||||
|
|
Приводя к общему знаменателю простейшие дроби и приравнивая |
|||||||||||||||||||||||||
числители (то есть отбрасывая одинаковые знаменатели), получим |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
x |
1 |
|
|
A x |
1 x |
3 |
|
Bx x |
3 |
|
|
Cx x 1 |
(10) |
||||||||
Найдем теперь неизвестные коэффициенты. Это можно сделать двумя способами.
11

1–й способ. Так как многочлены в левой и правой частях последнего соотношения тождественно равны, то они равны при всех значениях x, входящих в это соотношение, в том числе и при x 0, x 1, x 3 . Подставляя поочередно эти значения x в левую и правую части тождества (10), мы видим, что в правой части (10) остается отличным от нуля только одно слагаемое:
x |
0 |
1 |
A 3 |
A |
1/ 3 |
x |
1 |
2 B |
2 |
B |
1 |
x |
3 |
4 |
C 3 2 |
C |
2/ 3 |
Подставляя найденные коэффициенты в разложение дроби, имеем
|
|
|
x 1 |
1 |
|
|
1 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x3 |
4x2 |
3x 3x x 1 3 x 3 |
|
||||||||||
2–й способ. Произведем преобразование тождества (10): |
|
||||||||||||||
x 1 A x2 |
4x 3 Bx2 |
3Bx Cx2 Cx |
|
||||||||||||
|
|
A B C x2 |
|
4 A 3B C x 3A . |
|
||||||||||
Приравнивая коэффициенты при x2, x1 |
и x o (свободный член), по- |
||||||||||||||
лучим систему уравнений для определения коэффициентов A, B и C: |
|||||||||||||||
|
0 A |
B |
C |
|
|
|
|
|
|
0 1/ 3 |
B C |
||||
1 4 A 3B C |
|
|
|
|
|
|
|
1 4/ 3 3B C |
|||||||
|
1 |
3A |
|
|
|
|
|
|
|
|
|
|
A |
1/ 3 |
|
Складывая |
|
теперь |
первые |
два |
|
уравнения, |
получим |
||||||||
1 1 2B B |
1 . И, наконец, |
C 2 / 3 . Таким образом, получим тот |
|||||||||||||
же результат.
Вычисляя коэффициенты, можно комбинировать оба способа, это особенно удобно, если в разложении дроби на простейшие имеются простейшие дроби всех трех типов.
1
Пример 5. Разложить на простейшие рациональную дробь . x3 8
Решение: |
1 |
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x3 8 |
|
x |
2 x2 |
2x |
4 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Разложим дробь: |
|
|
1 |
|
|
|
|
|
A |
|
|
Bx C |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 2 x2 |
2x 4 x 2 x2 |
2x 4 |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||
Приводя простейшие дроби к общему знаменателю и приравнивая |
|||||||||||||||||||
числители, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
A x2 |
2x |
4 |
|
Bx |
|
C |
x 2 , |
|
(11) |
||||||
|
1 |
Ax 2 |
2Ax |
4A |
Bx 2 |
Cx |
2Bx |
2C, |
|
||||||||||
|
1 A B x |
2 |
2 A C 2B x 4 A 2C . |
(12) |
|||||||||||||||
|
|
|
|||||||||||||||||
12
