
Курс лекций по высшей математике. 2 часть
.pdf
Систему уравнений для определения A, B и C можно получить либо приравнивая коэффициенты при одинаковых степенях x в последнем тождестве, либо следующим образом. Положим в (11) x 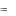 2 . Тогда 1 A 12 . Отсюда A 1/12 . Подставляя A в уравнения, которые полу-
2 . Тогда 1 A 12 . Отсюда A 1/12 . Подставляя A в уравнения, которые полу-
чаются из (12), если приравнять коэффициенты при x 2 и x0 получим:
0 A B |
0 |
1/12 |
B |
|
B 1/12 |
||||
1 4 A 2C |
|
|
1 4 /12 2C |
|
C 1/ 3 |
||||
Так что имеем окончательно: |
|
|
|
|
|
||||
|
1 |
|
|
1 |
|
1/12x |
1/ 3 |
. |
|
|
x3 |
8 12 x 2 |
|
x2 |
|
|
|||
|
|
2x 4 |
|||||||
ГЛАВА 2
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§1.Первообрàзная функция. Неопределенный интеграл
Основная задача дифференциального исчисления состоит в нахождении дифференциала данной функции или ее производной. Многочисленные вопросы науки и техники приводят к постановке обратной зада-
чи: для данной функции |
f x |
найти такую функцию F x , производная |
||||
которой равнялась бы f |
x . |
|
|
|
|
|
Функция F x |
называется первообрàзной для функции |
f |
x |
на |
||
данном промежутке, |
если для всех x из этого промежутка F |
x |
f |
x |
||
или, что то же самое, |
dF x |
f x dx. |
|
|
|
|
Естественно, возникает вопрос: для всякой ли функции существует первообразная? Ответ на него для достаточно широкого класса функций дает следующая теорема.
Любая непрерывная на отрезке функция имеет на этом отрезке первообразную.
13

Очевидно, первообразная для данной функции определяется не од-
нозначно. Так, для функции |
f x |
cos x первообразной является не |
||||||||||||||||
только sin x, но и sin x |
|
3, и sin x |
|
|
, и вообще sin x |
С. |
|
|
||||||||||
|
|
4 |
|
|
||||||||||||||
Теорема. Если функция F x |
является первообразной для функции |
|||||||||||||||||
f x |
на отрезке |
a;b , |
то всякая другая первообразная для |
f x |
отли- |
|||||||||||||
чается от F x |
|
на постоянное слагаемое, то есть может быть пред- |
||||||||||||||||
ставлена в виде F x |
С, |
где C–постоянная. |
|
|
|
|
|
|||||||||||
Доказательство. По определению первообразной |
F x |
f x , то- |
||||||||||||||||
гда |
F x |
C |
|
F |
x |
C |
f x , |
то есть при любом C=const функция |
||||||||||
F x |
С также является первообразной для f x . Покажем, |
что перво- |
||||||||||||||||
образных другого вида нет. Если |
Ф x –любая другая первообразная |
|||||||||||||||||
функции |
|
|
f |
x , |
|
|
то |
|
|
Φ x |
f |
x , |
|
тогда |
||||
Ф x |
F x |
Ф x |
F |
x |
f x |
|
f x |
0 для любого x |
a;b , |
а это |
||||||||
значит, что Ф x |
F x |
|
const, то есть Ф x |
F x |
С. |
|
|
|||||||||||
Из теоремы следует, что выражение |
F x |
С, |
где F x –некоторая |
|||||||||||||||
первообразная функции |
f |
x , |
а C–произвольная постоянная, охватыва- |
|||||||||||||||
ет совокупность всех первообразных функции |
f x . |
|
|
|
|
|||||||||||||
Если |
F x –одна из первообразных функции |
f |
x , то выражение |
|||||||||||||||
F x |
С, |
где C–произвольная постоянная, называется неопределенным |
||||||||||||||||
интегралом от функции |
f |
x |
обозначается |
f x dx. |
|
|
|
|||||||||||
Таким образом, |
|
f |
x dx |
F x |
C, |
|
|
|
|
|
|
|||||||
|
f x |
называется подынтегральной функцией, |
f |
x dx – подынте- |
||||||||||||||
гральным |
выражением, |
x–переменной |
интегрирования, символ |
– |
||||||||||||||
знаком неопределенного интеграла.
Процесс нахождения неопределенного интеграла называется ин-
тегрированием функции.
Геометрически неопределенный интеграл y F x С представляет собой семейство «параллельных» кривых.
14
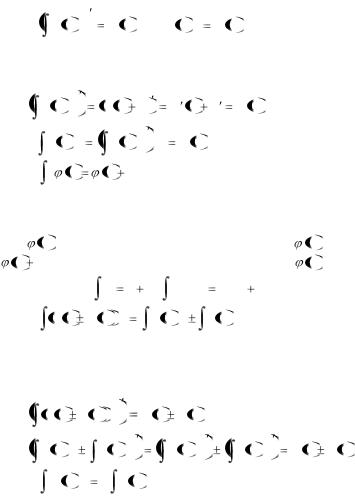
1. Свойства неопределенного интеграла
1. f x dx f x ; d
f x ; d  f x dx f x dx –производная неопределен-
f x dx f x dx –производная неопределен-
ного интеграла равна подынтегральной функции, а его дифференциал– подынтегральному выражению.
Доказательство. Из определения первообразной:
|
f x dx |
F x C |
F x C f x ; |
||
d |
f |
x dx |
f |
x dx dx |
f x dx. |
2. |
d |
x |
x |
C – неопределенный интеграл от дифференциала |
|
некоторой функции равен этой функции с точностью до постоянного слагаемого.
Доказательство. Из определения первообразной следует, что функ-
ция |
x |
является первообразной для функции d |
x , следовательно, |
||||
x |
C является неопределенным интегралом от d |
x . |
|||||
Например, |
dx |
x C, |
d cos x |
cos x C. |
|
||
3. |
f |
x |
g x dx |
f |
x dx |
g x dx –неопределенный интеграл |
|
от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от этих функций.
Доказательство. Достаточно показать, что совпадают производные
левой и правой частей равенства. |
|
|
|||
f x |
g x |
dx |
f x g x –по свойству 1; |
|
|
f x dx |
g x dx |
f x dx |
g x dx |
f x g x . |
|
4. kf |
x dx |
k f x dx , где k=const–постоянный множитель можно |
|||
вынести за знак неопределенного интеграла. Доказывается аналогично свойству 3.
Из свойств 1 и 2 следует, что дифференцирование и интегрирование являются взаимно обратными действиями.
15

2. Таблица основных неопределенных интегралов
1. |
dx |
x |
|
|
C; |
|
|
|
||||||||
2. |
|
xα dx |
|
|
|
|
|
xa 1 |
|
C, a |
1 ; |
|||||
|
|
|
|
|
a |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
|
dx |
ln |
|
x |
|
|
C; |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
a x |
|
|
|
|
|
|
|||
4. |
a x dx |
|
|
|
|
|
|
|
C; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
ln a |
|
|
|
||||||
5. |
|
e x dx |
|
|
|
|
|
e x |
|
|
C; |
|
|
|||
6. |
sin xdx |
|
|
|
|
cos x |
C; |
|
||||||||
7. |
|
cos xdx |
|
|
|
sin x |
C; |
|
||||||||
8. |
|
dx |
|
|
|
|
|
|
|
ctgx |
|
C; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
sin2 x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9. |
|
dx |
|
|
|
|
|
tgx |
C; |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
cos 2 |
x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
|
dx |
|
|
|
|
|
arctgx |
C; |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
1 x 2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
11. |
|
dx |
|
|
|
|
|
|
|
arcsin x |
|
|
C; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
x2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
12. |
|
|
dx |
|
|
|
|
|
|
|
|
1 |
|
arctg |
|
x |
|
C; |
||||||
a 2 |
|
x 2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
a |
|
|
|
a |
|
|
|
||||||||||||
13. |
|
|
dx |
|
|
|
arcsin |
x |
|
|
C; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|||||||||||||
|
a2 x2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
14. |
|
|
|
|
|
|
|
|
ln |
x |
|
|
x2 |
|
a |
C; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
2 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15. |
|
dx |
|
|
|
|
|
1 |
|
ln |
|
x |
|
a |
|
C; |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x2 |
a2 |
|
2a |
x |
|
a |
|
|||||||||||||||||
16. |
|
dx |
|
|
|
|
|
1 |
|
ln |
|
a |
|
x |
|
C; |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
a 2 |
x2 |
|
|
2a |
a |
|
x |
|
||||||||||||||||
17.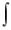 shxdx chx C;
shxdx chx C;
18. chxdx shx C;
19. |
|
dx |
thx C; |
|
|
|
|||
ch 2 x |
||||
|
|
|
||
20. |
|
dx |
cthx C. |
|
|
|
|||
|
sh2 x |
|||
|
|
|
Справедливость этих формул проверяется непосредственно: дифференцированием убеждаемся, что правые части равенств являются первообразными для соответствующих подынтегральных функций.
Например, для формулы 3: при x>0 ln |
x |
|
|
ln x |
и |
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
ln |
x |
|
C |
ln x |
; |
|
|
|
|
|
||||
|
x |
1 |
|
1 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
при x<0 ln |
x |
ln x и |
ln |
x |
C |
ln |
|
x |
1 |
|||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
16
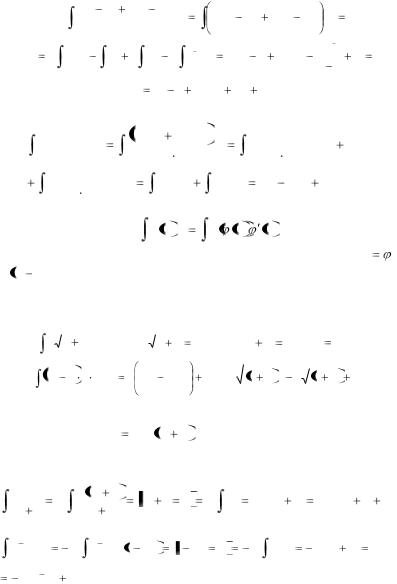
§2. Основные методы интегрирования
1.Метод разложения, или непосредственное интегрирование–
основан на применении свойств 3, 4 неопределенного интеграла. Пример 1.
|
|
|
3x6 |
|
x4 5x3 2x |
dx |
|
3x6 |
|
|
|
x4 |
|
5x3 |
|
|
|
|
|
2x |
|
dx |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
x4 |
|
|
x4 |
|
x4 |
|
|
|
|
|
x4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
3 x2 dx |
|
dx 5 |
|
dx |
|
2 x |
3 dx 3 |
x3 |
|
|
x 5ln |
|
x |
|
2 |
x 2 |
|
C |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x |
|
5ln |
x |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 2. |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dx |
|
|
|
|
sin2 x |
|
cos2 |
x dx |
|
|
|
|
|
sin2 |
x |
|
|
dx |
|
|
|||||||||||||||||||
|
sin2 x cos2 |
x |
sin2 |
x |
cos2 x |
|
|
|
sin2 x |
cos2 |
x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
cos2 |
x |
|
|
|
|
dx |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
tgx |
ctgx |
|
|
C |
|
|
|||||||||||||||||||
|
|
sin2 x |
cos2 x |
|
|
cos2 |
x |
|
sin2 |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||
2.Метод замены переменной–основан на использовании формулы |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f |
x dx |
f |
z |
|
|
z dz, |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||
где z–новая |
переменная, |
связанная с |
x |
соотношением |
x |
(z) , |
|||||||||||||||||||||||||||||||||||
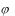 z
z непрерывная монотонная функция, имеющая непрерывную про-
непрерывная монотонная функция, имеющая непрерывную про-
изводную. Справедливость этой формулы следует из того, что равны дифференциалы ее левой и правой частей (проверьте).
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
z , тогда x |
3 |
z 2 , |
dx |
2zdz ]= |
||||||
x |
x |
3dx =[пусть |
x 3 |
||||||||||||||
|
|
|
z 5 |
|
z 3 |
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3 5 |
|
|
|
|
||||||
= z 2 |
3 |
z 2zdz 2 |
3 |
C = |
|
x |
2 |
x |
3 C . |
||||||||
|
|
|
|||||||||||||||
|
|
|
|
5 |
3 |
5 |
|
|
|
|
|
|
|
||||
На основании свойств дифференциала можно записать:
|
|
|
|
|
|
|
|
|
dx |
1 |
d kx |
c , где k, c–константы. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Покажем на примерах применение этого соотношения. |
|
|
|
|||||||||||||||||||||||||||||
|
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dx |
1 d 3x 5 |
|
1 |
|
dz |
|
|
1 |
|
|
|
1 |
ln |
|
3x 5 |
|
C |
||||||||||||||||
3x 5 z |
|
|
|
ln |
z |
C |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3x 5 3 3x 5 |
|
|
|
3 z |
3 |
|
|
3 |
|
|
|
|
|
||||||||||||||||||||
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
e1 4xdx |
|
1 |
|
e1 4xd 1 4x |
1 4x z |
|
1 |
ezdz |
1 |
ez |
C |
||||||||||||||||||||||
4 |
|
4 |
4 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 1 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
e |
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
17
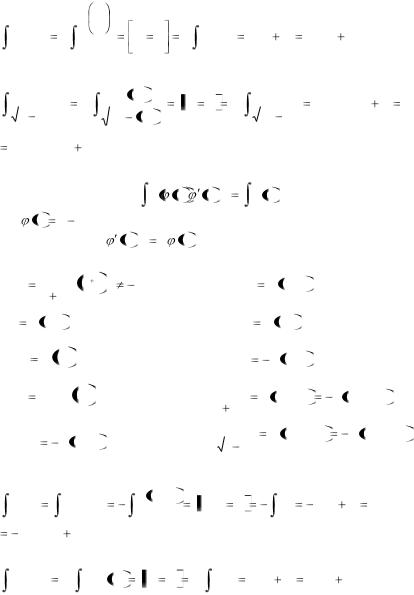
|
|
|
|
|
|
|
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
dx |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
x |
|
z |
|
2 |
|
|
dz |
|
|
|
|
|
2tgz |
C 2tg |
|
x |
C. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
cos |
2 x |
|
cos |
2 x |
|
2 |
|
|
cos 2 |
|
z |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Пример 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
d 5x |
|
|
|
|
|
5x |
|
z |
1 |
|
|
|
|
|
|
|
|
|
dz |
|
1 |
arcsin |
z |
C |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 25x2 |
5 |
|
|
|
|
|
22 5x 2 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
22 |
z 2 |
|
5 |
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
1 |
arcsin |
5x |
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Переобозначив переменные, формулу (1) можно записать в виде |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
x |
|
x dx |
|
|
|
|
f |
|
z dz, |
|
|
|
|
|
|
|
|
(2) |
||||||||||||||||
где |
|
|
|
|
|
x |
z |
|
новая переменная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Заметим, что |
|
x dx |
d |
|
|
x . Это преобразование называется под- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ведением под знак дифференциала. В частности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
xn dx |
|
|
|
1 |
|
|
|
|
d xn 1 , n |
|
1; |
|
|
|
|
|
|
|
|
cos xdx |
|
|
d sin x ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dx |
|
|
|
|
d ln x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
d tgx ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
e x dx |
|
|
|
d e x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
d ctgx ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a x dx |
|
|
|
1 |
|
|
d a x |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
d arctgx |
|
|
|
|
|
d arcctgx ; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
d arcsin x |
|
|
d arccos x ; |
||||||||||||||
|
sin xdx |
d cos x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
sin x |
|
|
|
d cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
tgxdx |
|
|
dx |
|
|
|
|
cos x |
|
|
|
z |
|
|
|
|
|
|
|
|
|
ln |
z |
C |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
ln |
cos x |
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x4 |
|
3 |
|
|
|
|
1 |
|
|
|
x4 |
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
1 |
|
|
z |
|
|
|
|
|
|
1 |
|
|
z |
|
|
|
|
1 |
|
|
|
x4 |
|
|
|
||||||||||||||
|
e |
|
|
|
x |
dx |
|
|
|
|
|
|
|
e |
|
d x |
|
|
|
x |
|
|
|
z |
|
|
|
|
e |
dz |
|
|
|
|
|
|
|
e |
|
C |
|
|
e |
|
|
C. |
|
|||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
4 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
18
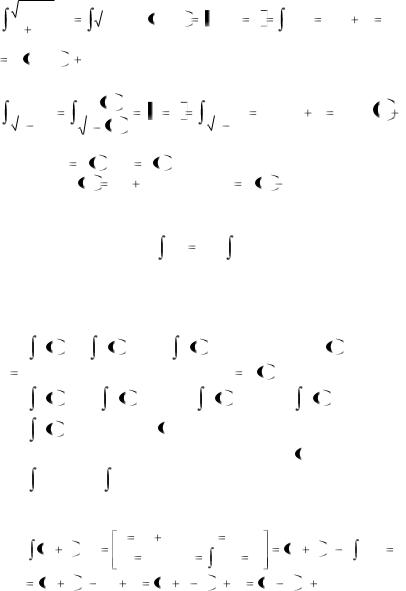
Пример 3.
|
|
|
arctgx dx |
|
|
arctgx d arctgx |
arctgx |
|
z |
z 2 dz |
2 z 2 |
C |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
arctgx 2 |
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Пример 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ex dx |
|
d ex |
ex |
z |
|
dz |
|
arcsin z C |
|
arcsin ex C. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 e2 x |
1 ex 2 |
1 z 2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3.Метод интегрирования по частям. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Если u |
u x |
и v |
v x –функции, имеющие непрерывные произ- |
||||||||||||||||||
водные, то d uv |
vdu |
udv , |
тогда |
udv |
d uv |
vdu ; проинтегрировав |
||||||||||||||||||||
это равенство и учитывая свойство 2 неопределенного интеграла, полу-
чим формулу интегрирования по частям:
udv uv  vdu.
vdu.
Иногда эту формулу приходится применять последовательно несколько раз.
Отметим три типа интегралов, которые вычисляются методом интегрирования по частям.
P x ekxdx, |
P x sin kx dx, P x cos kx dx, |
где |
P x –многочлен, |
k const. В этих интегралах полагают u P x . |
|
|
|
P x ln xdx, |
P x arcsin xdx, P x arccos xdx, |
P x arctgxdx, |
|
P x arcctgxdx, где P x –многочлен. В этих интегралах за u при-
–многочлен. В этих интегралах за u при-
нимают функцию, являющуюся множителем при P x .
.
emx cos nxdx, emx sin nxdx, |
где m, |
n–числа. Эти интегралы вычис- |
|||||||
ляются двукратным интегрированием по частям. |
|
||||||||
Пример 1 |
|
|
|
|
|
|
|
|
|
3x 1 ex dx |
u |
3x 1; |
|
du |
3dx |
|
3x 1 ex 3 ex dx |
||
dv e |
x |
dx; |
v |
x |
dx e |
x |
|||
|
|
e |
|
|
|||||
3x 1 ex 3ex |
|
C 3x 1 3 ex |
C 3x |
2 ex C. |
|||||
19

Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u |
ln x; |
|
|
|
|
du |
|
dx |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
4x3 |
2x |
|
1 ln xdx |
|
|
|
|
|
|
|
|
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
dv |
4x3 |
2x |
1 dx; |
v |
|
|
dv |
x4 |
|
x2 |
x |
||||
|
x4 |
x2 |
x ln x |
|
|
x4 |
|
x2 |
x |
dx x4 x2 |
x ln x |
x3 |
|
x 1 dx |
||||||||||
|
|
|
|
|
|
x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x4 |
x2 |
x ln x |
|
x4 |
|
|
x2 |
|
x C. |
|
|
|
|
|
|
|
|
|
|
||||
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ex sin xdx |
|
u |
ex ; |
|
|
|
du |
ex dx |
|
|
ex cos x |
|
ex cos xdx |
|||||||||||
dv |
|
sin xdx; |
v |
|
|
sin xdx |
cos x |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
u |
ex ; |
|
|
du |
ex dx |
|
|
ex |
cos x ex |
sin x |
ex sin xdx; |
|
||||||||||||
dv |
cos xdx; |
|
v |
cos xdx sin x |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Таким |
|
|
|
|
|
|
|
|
|
образом, |
|
|
|
|
|
|
|
получили: |
||||||
ex sin xdx |
ex |
sin x |
cos x |
|
|
ex sin xdx; |
перенесем последнее слагае- |
|||||||||||||||||
мое в левую часть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
e x sin xdx |
e x |
sin x |
|
cos x |
|
C; e x sin xdx |
|
|
1 |
e x sin x |
cos x |
C. |
|||||||||||
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
§3. Интегрирование рациональных дробей
|
|
|
|
|
|
|
Ρn |
x |
|
Рациональной |
дробью называется выражение вида |
|
|
, где |
|||||
|
|
||||||||
|
|
|
|
|
|
|
Qm |
x |
|
Pn x , Qm x –многочлены степеней n и m соответственно. |
|
|
|||||||
Если n |
m , рациональная дробь называется правильной, в против- |
||||||||
ном случае |
n m –неправильной. |
|
|
||||||
Если дробь неправильная, из нее можно выделить целую часть, |
|||||||||
разделив числитель на знаменатель. |
|
|
|||||||
Например, |
x4 |
3x3 |
5x 1 |
–неправильная рациональная |
дробь. |
||||
|
x2 |
3 |
|
||||||
|
|
|
|
|
|
|
|
||
Выполним деление:
20

– |
x4 |
3x3 |
5x 1 |
|
x 2 |
3 |
x4 3x2 |
|
|
x2 |
3x 3 |
||
|
|
|
||||
– |
3x3 |
3x 2 |
5x 1 |
|
|
|
3x3 |
|
|
|
|
|
|
|
9x |
|
|
|
|
|
– |
3x 2 |
14x |
1 |
|
|
|
3x 2 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
14x |
8 |
|
– |
остаток |
|
Таким образом, неправильную дробь можно представить в виде суммы целой рациональной функции (многочлена) и правильной дроби:
|
|
|
|
|
|
|
|
x4 |
3x3 |
|
|
5x 1 |
|
x2 |
|
3x 3 |
|
|
|
14x 8 |
. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
3 |
|
|
|
|
|
|
|
||||||
|
Простейшими рациональными дробями называются правильные |
|||||||||||||||||||||||||||||||||||||||||
рациональные дроби следующих четырех типов: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Α |
, |
|
|
|
|
Α |
|
|
, |
|
|
|
|
|
|
|
Bx C |
, |
|
|
|
|
|
|
|
|
Βx C |
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
a k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
a |
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
2 |
|
px |
q |
|
|
|
|
|
|
x |
2 |
px |
q |
k |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
где A, B, C, a, p, q–числа, |
k |
N, k |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Покажем на примерах, как интегрируются дроби каждого типа. |
|||||||||||||||||||||||||||||||||||||||||
|
Дробь 1–го типа: |
|
|
3dx |
|
|
d x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
3 |
|
|
3ln |
x 5 |
|
C. |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x |
|
5 |
|
|
|
x |
5 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Дробь 2–го типа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dx |
|
|
1 |
|
2x |
3 |
4 |
d 2x |
3 |
|
|
|
|
1 |
|
2x |
3 |
|
3 |
|
C |
|
|
|
|
1 |
|
|
|
C. |
|||||||||||
|
2x 3 4 |
2 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
6 2x 3 3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Дробь 3–го типа: |
|
|
|
|
3x |
1 |
|
|
|
dx |
=[выделим в знаменателе полный |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
x 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
квадрат и введем новую переменную: x2 |
4x+13= x 2 2+9 ; |
x 2 z, |
||||||||||||||||||||||||||||||||||||||||
x z |
2, |
|
3x 1 3 z |
|
|
2 |
1 |
3z 5, dx |
dz ]= |
|
3z |
|
5 dz |
=[разобьем |
||||||||||||||||||||||||||||
|
|
|
|
z 2 |
|
9 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
интеграл на сумму двух интегралов, первый из которых вычислим под-
ведением |
|
под |
|
|
|
знак |
|
|
дифференциала, |
|
второй–табличный]= |
|||||||||||||||||
3 |
|
zdz |
5 |
|
dz |
|
|
3 |
|
d z2 |
9 |
|
5 |
arctg |
z |
|
3 |
ln z2 |
9 |
5 |
arctg |
z |
C |
|||||
z2 9 |
|
z2 |
9 2 |
|
|
z2 |
9 |
3 |
3 |
|
2 |
3 |
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
3 |
ln x2 |
4x |
13 |
|
5 |
arctg |
x |
2 |
|
C. |
|
|
|
|
|
|
|
|
|
||||||||
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|

Дроби 4–го типа интегрируются с помощью специальной рекуррентной формулы, которую мы рассматривать не будем.
Если правильная дробь не является простейшей, ее представляют в виде суммы простейших дробей.(См Гл.I, §2, 30)
Пример. |
dx |
|
. |
|
|
||
x2 4x 3 x2 |
|
||
|
4x 5 |
||
Подынтегральная функция–правильная рациональная дробь. Представим ее в виде суммы простейших дробей, учитывая, что x2 4x 3 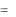 x 1 x 3 .
x 1 x 3 .
1 |
|
|
A |
|
B |
|
Cx |
D |
; |
|
|
|
|
|
|
|
|
|
|
x 1 x 3 x2 |
4x 5 x 1 x 3 |
|
x2 |
4x 5 |
|||||
|
|
||||||||
приведем к общему знаменателю сумму дробей, стоящих в правой части:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 x |
3 x2 |
|
|
4x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
A x 3 x2 4x 5 B x 1 x2 |
4x 5 Cx D x 1 x 3 |
; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 1 x |
3 x2 |
|
|
4x |
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
приравняем числители дробей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A x 3 x2 |
4x 5 B x 1 x2 |
|
4x 5 |
|
|
Cx D x 1 x 3 1; |
||||||||||||||||||||||||||||||
при x |
|
1 получим: |
20A |
1; A |
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при x |
|
3 получим: |
52B |
1; B |
|
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приравняем коэффициенты при x 3 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
A B C 0; C |
A B |
|
1 1 |
|
|
8 |
|
|
|
|
2 |
. |
|
|
||||||||||||||||||||
|
|
|
20 |
|
|
|
|
52 |
|
|
260 |
|
65 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
приравняем свободные члены: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
15 |
|
5 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
15A 5B |
|
|
|
|
|
|
|
|
|
|
52 39 5 |
|
|
||||||||||||||||
|
15A 5B |
3D |
1; D |
20 |
|
52 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
52 3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
18 |
|
|
|
6 |
|
|
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
52 3 |
|
52 |
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
22
