Развертки.

Призматические поверхности возможно разворачивать в плоскую фигуру по двум схемам.

1 схема: а) пересечь поверхность плоскостью, перпендикулярной к ребрам;

б) определить длины отрезков линии сечения призмы этой плоскостью;

в) линию сечения развернуть в прямую и на перпендикулярах в точках пересечения ребер призмы и плоскости сечения отложить длины отрезков соответствующих ребер;

г) соединить основания и вершины ребер прямыми.

2 схема: а) грани призмы разбить на треугольники;

б) определить длины сторон этих треугольников;

в) построить последовательно треугольники способом линейных засечек.

П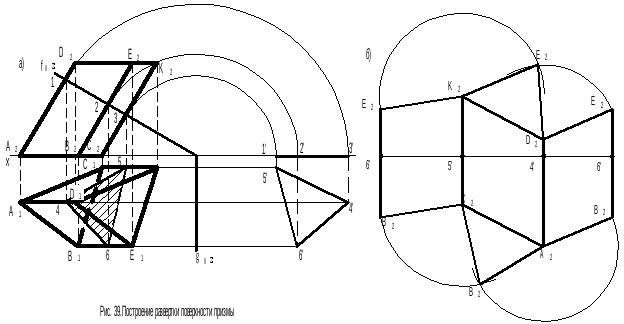ример развертывания призмы по первой схеме.

Дано (рис 39): призма с основаниями ABCиDEK. Построить ее развертку.

Решение. 1. Пересечем призму фронтально проецирующей плоскостью Σперпендикулярной к ребрам призмы (на рисунке показана следамиf _0Σиg _0Σ). Построим проекции фигуры сечения призмы плоскостью1-2-3и4-5-6(рис 39,а).

2. Способом вращения вокруг фронтально проецирующей прямой определим истинные размеры фигуры сечения 4-5-6.

3. Ломаную линию фигуры сечения 4-5-6развернем в прямую (рис. 39,б).

4. От точек сечения 6-5-4-6построим перпендикуляры к линии сечения, причем6E₂=2E₂,

6B₂=2B₂,5K₂=3K₂,5C₂=3C₂и т.д.

5. Соединив концы отрезков получаем развертку боковой поверхности призмы B₂E₂K₂D₂E₂B₂A₂C₂B₂.

6. Способом линейных засечек строят основания призмы - B₂A₂C₂,Е₂K₂D₂.

Пример построения развертки способом засечек.

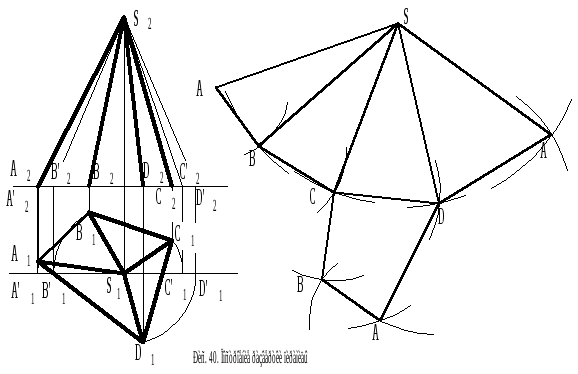
Дано. Пирамида с основанием ABCDи вершинойS. Необходимо построить ее развертку.

Решение (рис. 40). 1. Вращают пирамиду вокруг ее высоты проходящей через точку Sдо положения, когда каждое из реберA₁S₁,B₁S₁…. становится параллельным фронтальной плоскости,…..

2. Строят их фронтальные проекции ,…., которые равны истинным длинам ребер.

3. Строят первую сторону развертки AS=A′₂S₂. Из точкиАделают линейную засечку радиусомА₁В₁, из точкиSделают засечку радиусом. Получают точкуВ. Затем, опираясь на точкиВиSполучают точкуСи т.д.

4. Соединив все точки прямыми получают развертку боковой поверхности пирамиды.

5. Способом линейных засечек строят основание пирамиды.

Примеры решения задач.

Задача 1. Дано: точки А(15,25,20),В(30,-25,-10),С(20,-15,25). Необходимо построить проекции точек на трех плоскостях проекций.

Р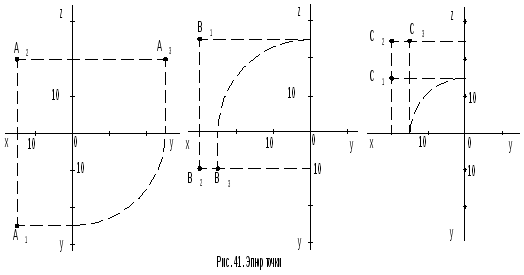ешение (рис.41). 1. Форма записи координат точек в общем виде следующая:А(X,Y,Z). Откладывают на осяхx,y,zнеобходимые величины и на пересечении координатных линий строят соответствующие проекции точек. При этом учитывают, что в противоположных направлениях от точки пересечения координатных осей разные по знаку значения координат, на рисунке подписаны положительные направления осей. ПлоскостьП₁образуется осямиx,y; плоскостьП₂– осямиx,z; плоскостьП₃– осямиy,z. Осьyпоказывается дважды, поскольку по ней происходит «разрыв» объемного изображения. Разрыв целесообразно показывать дугой.

Задача 2. Дано (рис.42): прямая АВи точкиС,Dво фронтальной и горизонтальной проекциях. Необходимо определить принадлежность точекС,DпрямойАВ.

Решение. Строят профильные проекции С₃,D₃точек иА₃В₃прямой. Все одноименные проекции прямойАВи точкиСсовпадают, поэтому точкаСпринадлежит прямойАВ. Профильная проекция точкиDлежит вне прямой, поэтому точкаDне принадлежит прямойАВ.

З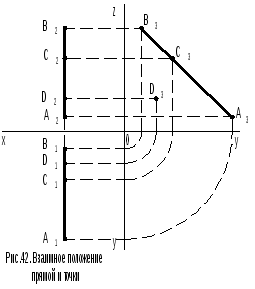адача 3. Дано (рис.43): прямыеАВиCD. Необходимо пересечь их третьей прямой, отстоящей на расстоянииLот плоскостиП₁.

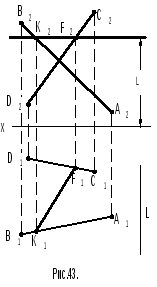Решение. 1. На расстоянииL от осихи параллельно ей строят фронтальную проекцию искомой прямой, которая пересекает данные прямые в точкахK₂,F₂.

2. Строят горизонтальные проекции К₁,F₁; прямая, проходящая через эти точки является горизонтальной проекцией искомой прямой.

З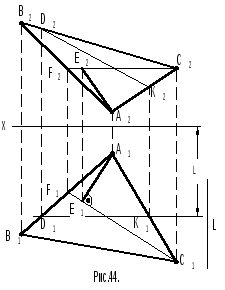адача 4. Дано (рис.44): треугольникомАВСзадана плоскость. Необходимо построить фронталь этой плоскости, удаленную от плоскости проекцийП₂на расстояниеLи линию ската плоскостиАВС.

Р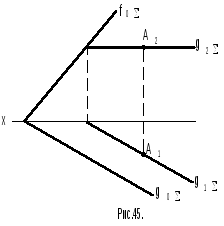ешение. 1. На плоскости проекцийП₁на расстоянииLот осихстроят горизонтальную проекцию фронтали, которая пересекает стороны треугольника в точкахD₁,K₁.

2. Строят фронтальную проекцию фронтали D₂K₂.

3. Линия ската плоскости перпендикулярна ее горизонтали. Поскольку горизонталь параллельна плоскости П₁, то этот прямой угол без искажений изобразится именно на плоскостиП₁. Строят фронтальную проекцию горизонталиС₂F₂. Строят ее горизонтальную проекциюC₁F₁.

4. Из точки А₁проводят перпендикулярА₁Е₁к горизонтальной проекции горизонталиC₁F₁. Строят фронтальную проекциюА₂Е₂. ПрямаяАЕявляется линией ската плоскостиАВС.

Задача 5 (рис.45). Дано: плоскостьзадана следами, известна горизонтальная проекцияА₁точкиА, принадлежащей плоскости. Необходимо построить фронтальную проекцию точкиА.

Решение. 1. След плоскости является горизонталью плоскостинулевого уровня. Параллельно ему через точкуА₁проводят горизонтальную проекциюгоризонтали плоскости.

2. Строят фронтальную проекцию горизонтали, зная, что она параллельна осих.

3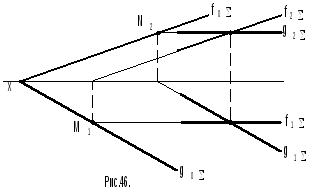. На фронтальной проекции горизонтали строят фронтальную проекциюА₂точкиА, из условия, что она лежит на горизонтали плоскости.

Задача 6 (рис.46). Дано: плоскостьзадана ее горизонтальюgи фронтальюf. Необходимо построить следы плоскости.

Решение. 1. Строят след горизонтали N₂и след фронталиM₁.

2. Строят горизонтальный след плоскостииз условия, что он пройдет через след фронталиМ₁и является параллельным горизонтальной проекции горизонталиg₁.

3. Строят фронтальный след плоскостииз условия, что он пройдет через след горизонталиN₂и параллелен фронтальной проекции фронталиf₂. Контроль построений - горизонтальный и фронтальный следы плоскости должны пересечься на осих.

З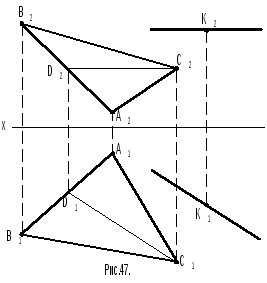адача 7 (рис.47). Дано: треугольникомАВСзадана плоскость, вне ее находится точкаК. Необходимо через точкуКпровести прямую параллельную треугольникуАВСи плоскостиП₁.

Решение. 1. Для выполнения обоих условий параллельности прямая, проходящая через точку Кдолжна быть параллельна горизонтали треугольникаАВС. Строят фронтальную проекциюС₂D₂ горизонтали, затем ее горизонтальную проекциюС₁D₁.

2. Через проекции К₁,К₂проводят прямые параллельные одноименным проекциям горизонталей треугольникаАВС. Прямая, проходящая через точкуКодновременно параллельна и треугольникуАВСи плоскости проекцийП₁.

Задача 8 (рис.48). Дано: ТреугольникомАВСзадана плоскость, вне ее находится прямаяЕК. Необходимо найти точку пересечения прямой и плоскости.

Р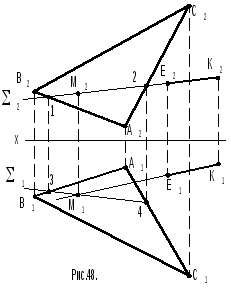ешение. 1. Через прямуюЕКпроводят вспомогательную фронтально проецирующую плоскость, строят фронтальную проекцию 1-2 линии пересеченияАВСи плоскости.

2. Строят горизонтальную проекцию 3-4 линии пересечения плоскости иАВС. Находят горизонтальную проекциюМ₁точки пересечения прямойЕКиАВС.

3. Строят фронтальную проекцию М₂точки пересечения прямойЕКиАВС.

Задача 9 (рис.49). Дано: плоскостьзадана следами, вне ее находится прямаяЕК. Необходимо найти точку пересечения прямой и плоскости.

Решение. 1. Через прямую ЕКпроводят одну из проектирующих плоскостей (в примере – фронтально проецирующая плоскость). Фронтальная проекция линии пересечения плоскостейипроходит через точкиN₂иM₂и совпадает сЕ₂К₂.

2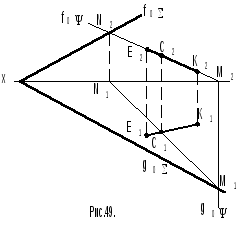. Строят горизонтальную проекциюN₁M₁линии пересечения плоскостейии определяют точкуС₁, являющуюся горизонтальной проекцией точки пересечения прямойЕКи плоскости.

3. Строят фронтальную проекцию С₂точки пересечения прямойЕКи плоскости.

Задача 10 (рис.50). Дано: плоскостьзадана ее горизонтальюgи фронтальюf,вне ее находится прямаяMN. Необходимо определить угол между прямой и плоскостью.

Решение. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на данной плоскости. Чтобы построить такой угол нужно получить точку пересечения прямой с данной плоскостью и точку пересечения перпендикуляра, проведенного из любой точки данной прямой к плоскости. 1. Строится точка Кпересечения прямойMNи данной плоскости, для чего через прямуюMNпроводят вспомогательную проецирующую плоскость (в примере – горизонтально проецирующая плоскость ). Подробно этот этап не описывается, поскольку принцип его решения аналогичен решению задачи №8.

2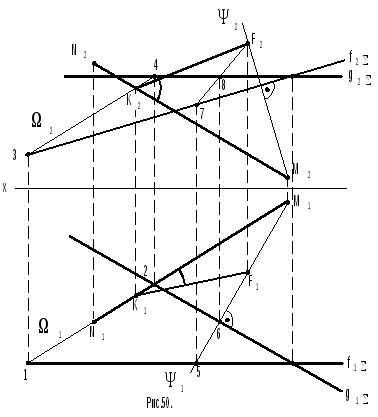. Из точкиМпроводят перпендикуляр к исходной плоскости, при этом используется правило о том, что горизонтальная проекция перпендикуляра к плоскости перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали.

3. Определяют точку Fпересечения перпендикуляра и исходной плоскости, для чего строят вспомогательную проецирующую плоскость (в примере – горизонтально проецирующая плоскость ). УголMKFявляется искомым углом между прямой и плоскостью.

З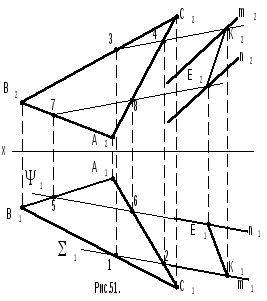адача 11 (рис.51). Дано: первая плоскость задана треугольникомАВС, вторая - параллельными прямымиmиn. Необходимо построить линию их пересечения.

Р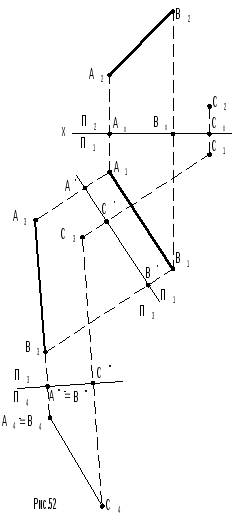ешение. 1. Строят точку пересечения прямойmи треугольникаАВС, для чего через прямуюmпроводят вспомогательную проецирующую плоскость (в примере горизонтально проецирующая плоскость). Получают горизонтальную линию 1-2 пересечения плоскостиАВСи.

2. Строят ее фронтальную проекцию 3-4 и находят фронтальную проекцию К₂точки пересечения прямойmи плоскостиАВС. Строят ее горизонтальную проекциюК₁.

3. Определяют точку Епересечения прямойnи плоскостиАВС, для чего проводят вспомогательную горизонтально проецирующую плоскость(графические построения аналогичны выше описанным). ТочкиЕиКобщие для обеих исходных плоскостей, то есть линияЕКэто линия их пересечения.

Задача 12 (рис.52). Дано: прямаяАВи точкаС. Необходимо определить кратчайшее расстояние от точки до прямой способом перемены плоскостей проекций.

Решение. 1. Вводят дополнительную плоскость П₃П₁и одновременно плоскостьП₃параллельна отрезку АВ (поэтому осьП₁/П₃параллельна отрезкуА₁В₁). Строят проекцииА₃В₃иС₃на плоскостиП₃из условия, что,,. На плоскостиП₃отрезокАВизобразится в натуральную величину.

2. Вводят дополнительную плоскость П₄перпендикулярную отрезкуАВ(одновременноП₄П₃), при этом отрезкаАВна плоскостиП₄будет точка. Построения точекА₄В₄иС₄выполняют из условия, что

,. ОтрезокА₄С₄есть кратчайшее расстояние от точкиСдо прямойАВ.

З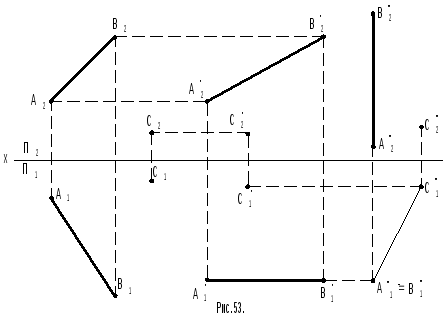адача 13 (рис.53). Дано: Дана прямаяАВи точкаС. Необходимо определить кратчайшее расстояние от точкиСдо прямойАВспособом вращения (в вариации плоскопараллельного перемещения).

Решение. 1. Вращают прямую АВи точкуСвокруг произвольной оси перпендикулярной плоскостиП₁до положения когда прямаяАВстанет параллельна плоскостиП₂(то есть проекциябудет параллельна осих). Само вращение не показывают, зная, что взаимное положение точекА₁В₁С₁не изменится, но они перейдут в позицию.

2. Строят фронтальные проекции и.

3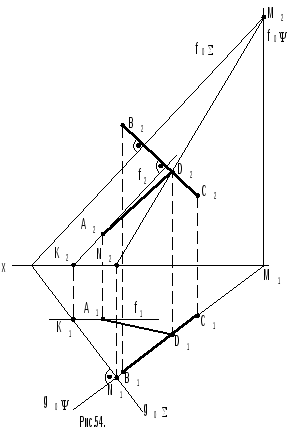. Вращают новое положение прямойАВи точкиСвокруг произвольной оси перпендикулярнойП₂до положения когда прямаяАВстанет перпендикулярнойП₁(то есть проекциябудет перпендикулярна осих). Взаимное положение точекпри этом не изменится, но они перейдут в позицию.

3. Строят горизонтальные проекции и. Расстояниеесть искомое кратчайшее расстояние от точкиСдо прямойАВ.

Задача 14 (рис.54). Дано: точкаАи прямаяВС. Необходимо из точкиАпостроить перпендикуляр к прямойВС.

Решение. В основу решения этой задачи может быть положен следующий принцип: перпендикуляр к плоскости, опущенный из данной точки, будет перпендикулярен любой прямой этой плоскости, в том числе и проходящей через основание этого перпендикуляра.

1. Через точку Апроводят плоскость, перпендикулярную прямойВС, для этого: а) через точкуАпроводят фронтальf, при условии, что фронтальная проекцияf₂фронталиfдолжна быть перпендикулярна фронтальной проекцииВ₂С₂прямойВС;

б) строят горизонтальный след К₁фронталиfи через него проводят горизонтальный следплоскостипри условии, что он должен быть перпендикулярен горизонтальной проекцииВ₁С₁прямойВС;

в) строят фронтальный след плоскостипри условии, что он должен быть параллелен фронтальной проекцииf₂фронталиf.

2. Определяют точку пересечения прямой ВСи плоскости, для этого: а) через прямую ВС проводят вспомогательную проецирующую плоскость(в примере – горизонтально проецирующая,,- ее следы);

б) строят линию MNпересечения плоскостейи;

в) определяют точку D₂пересечения фронтальных проекций линииMNи прямойВС, строят ее горизонтальную проекциюD₁.

3. Строят отрезок AD, который является искомым перпендикуляром из точкиАна прямуюВС, причем точкаDесть основание этого перпендикуляра.