9.4. Тройные интегралы

9.4.1. Вычисление тройного интеграла в декартовой системе координат

Пусть существует тройной интеграл

, (25)

где - некоторая функция, заданная в пространственной области интегрирования .

В

Рис.29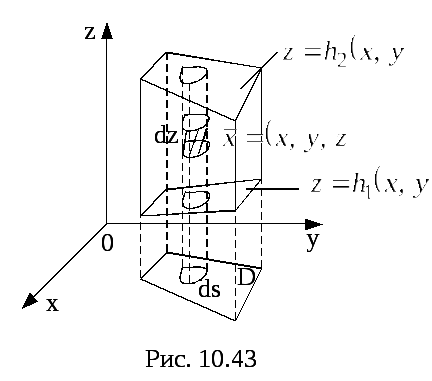

еличина интеграла (25) есть масса тела, если подынтегральную функцию рассматривать, как плотность распределения массы. Пусть областьограничена поверхностямиснизу исверху, и боковой цилиндрической поверхностью или совокупностью нескольких цилиндрических поверхностей (рис.29). Функцииизаданы в областиD, которая является проекцией области на плоскостьОху. Каждая прямая, выходящая из внутренней точки области D пересекает границу области в двух точках. Возьмем бесконечно малый элементвD и вычислим массу стержня вырезанного из цилиндрической поверхностью, у которого направляющей является граница элемента, а образующая параллельна оси Oz.

Выделим на высоте из нашего стержня элемент длины. Объём его равен, а масса будет равна(плотность массы в элементе объёмаможно считать постоянной ввиду его малости).

Чтобы найти массу всего стержня необходимо просуммировать все такие элементы, т.е. вычислить интеграл

.

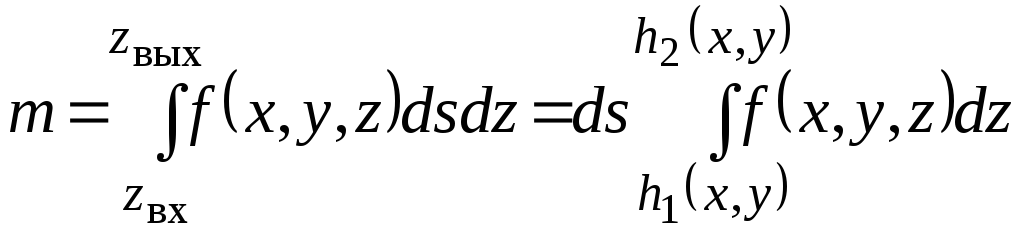Здесь х и у считаются постоянными, так как интегрирование происходит по z. Чтобы определить массу всего , надо просуммировать массы всех узких стержней, опирающихся на всевозможные площадиds, тогда получаем

,

.

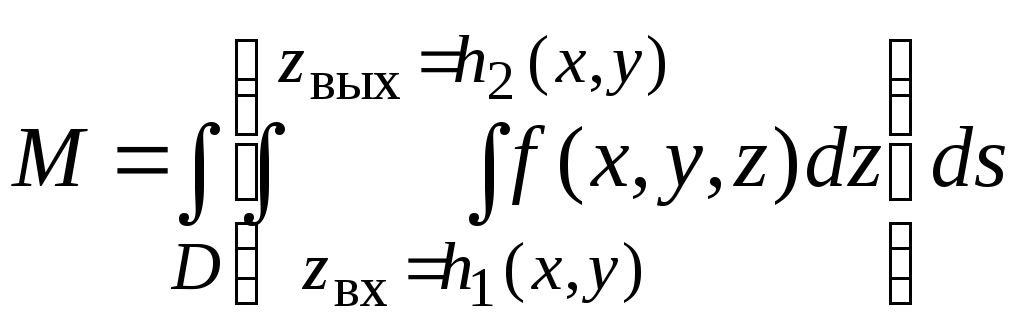Тогда

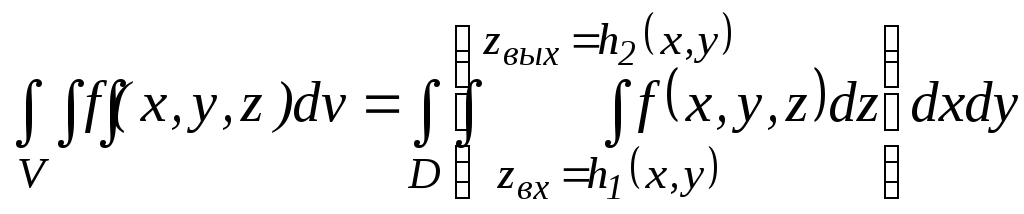. (26)

Таким образом, чтобы вычислить тройной интеграл, интегрируют поz от точки входа до точки выхода, считая х и у постоянными, затем от полученного результата вычисляют двойной интеграл по проекции области на плоскостьОху. Это один из способов вычисления тройных интегралов.

В случае, когда область ограничена поверхностями,, цилиндрическими поверхностями вдоль оси, интеграл (25) вычисляется по формуле

.

Если же область задана функциями,, и цилиндрическими поверхностями вдоль оси, то соответственно получаем для (25):

.

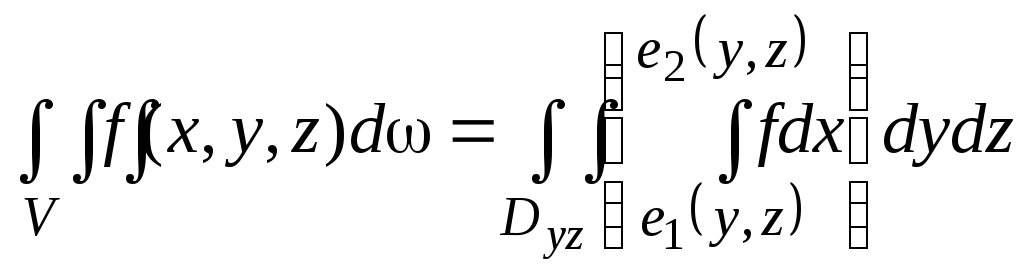
Пример 13. Вычислить тройной интеграл , где– область, ограниченная поверхностями,,,.

Решение. Область (рис. 30) можно записать в виде

Рис.30

,

где . Сводя тройной интеграл к повторному интегралу, получим

.

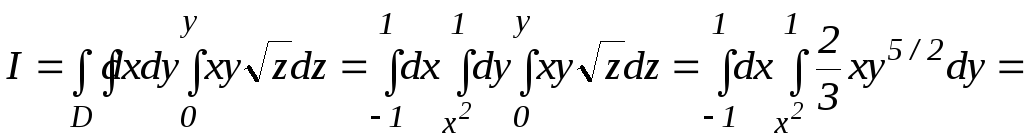
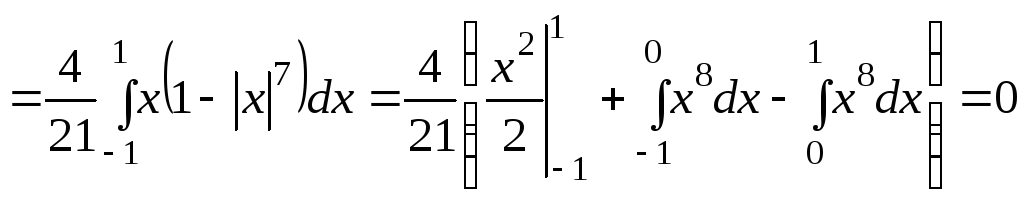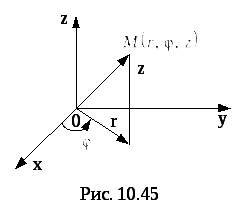
9.4.2. Вычисление тройного интеграла в цилиндрической и сферической системах координат. Кроме декартовой системы координат для описания положения точки в пространстве используются и другие системы координат, которые называются криволинейными системами координат. Наиболее распространёнными являются цилиндрическая и сферическая системы координат. Положение точки в цилиндрической системе координат определяетсяполярными координатами проекцииточки М наплоскость и расстоянием точки М до плоскости (рис.31). Числа называются цилиндрическими координатами точки. Цилиндрические координаты связаны с декартовыми следующими отношениями

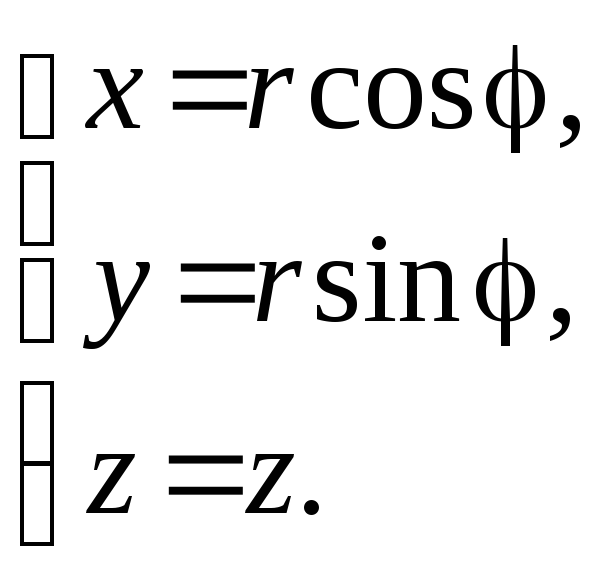
В

Рис.31

ряде случаев вычисление тройного интеграла в цилиндрической системе координат упрощается по сравнению с вычислением того же интеграла, но в декартовой системе координат. Пусть

,

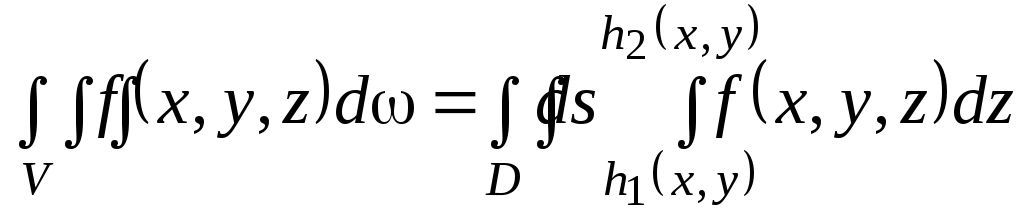где ,- аппликаты точек входа и выхода из области. Применив формулы перехода, получим:

.

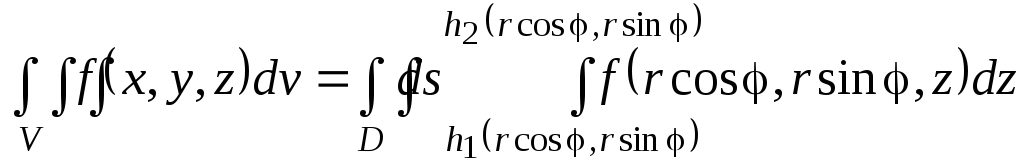Двойной интеграл вычисляем его в полярной системе координат:

.

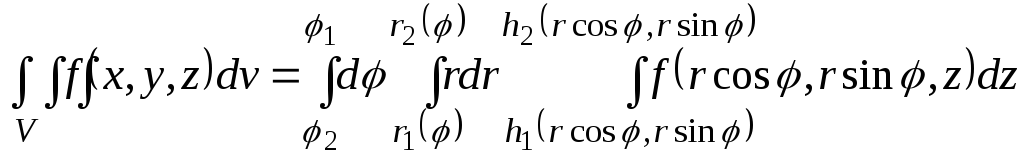Это и есть формула для вычисления тройного интеграла в цилиндрической системе координат.

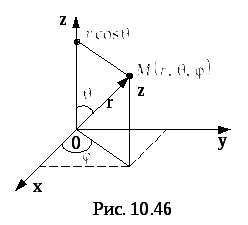
Другая распространённая система координат - сферическая. Положение точки в сферической системе координат определяется расстоянием от начала координат - , полярным угломпроекции её на плоскость и углом между осью и радиус-вектором точкиМ, отсчитанным от положительного направления оси, т.е. (рис. 32).

П

ределы изменения параметров в сферической системе координат следующие:,,. Связь между сферической системой координат и декартовой выражается следующим образом:

Рис.46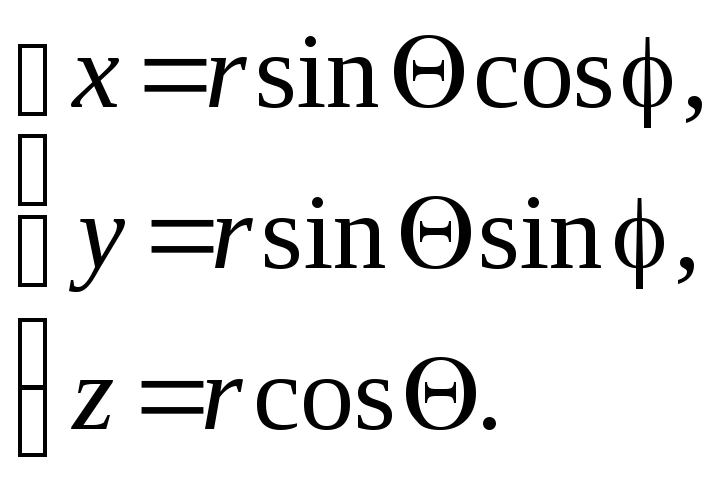

Имеет место формула для вычисления тройного интеграла в сферической системе координат

,

,

так как ябобиан преобразования

.

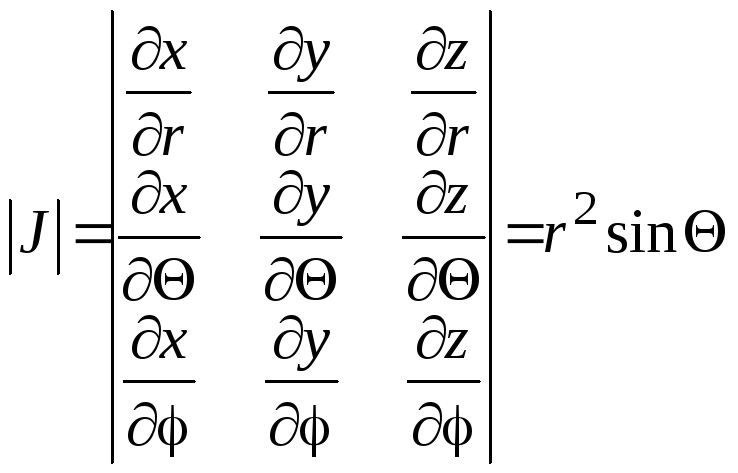Пример 14. Вычислить интеграл , если областьограничена поверхностямии.

Решение. Область V представляет собою конус (рис.33а). Уравнение конической поверхности, ограничивающей область , можно записать в виде, а саму областьпредставить следующим образом:, где– круг радиуса 1 с центром в начале координат. Поэтому данный тройной интеграл можно свести к последовательному вычислению трех определенных интегралов в прямоугольных координатах:

.

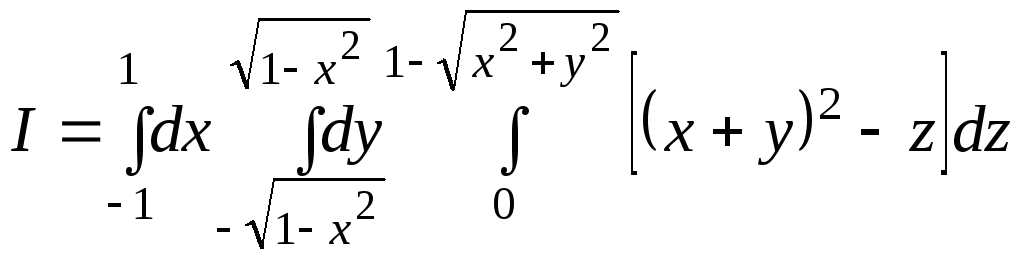Рис.33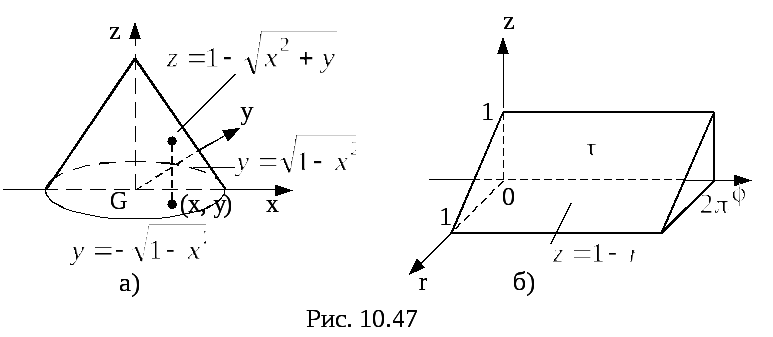

Однако удобнее перейти к цилиндрическим координатам :,,. Тогда прообраз кругаесть прямоугольник, прообраз конической поверхности – плоская поверхность, а прообраз области, область(рис.33б). Якобиан перехода к цилиндрическим координатам равен , подынтегральная функция в цилиндрических координатах равна. Сводя тройной интеграл по областик последовательному вычислению трех определенных интегралов, получим

.

Отметим, что расстановку пределов интегрирования в цилиндрических координатах можно произвести, рассматривая не область , а изменение цилиндрических координат в области. Наглядно видно, что в областипеременнаяизменяется от 0 до, при каждом значениипеременнаяизменяется от 0 до 1, а для каждой точкиобластипеременнаяизменяется в областиот 0 (значение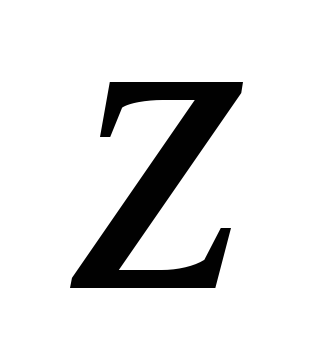в области) до(значениена конической поверхности).

9.4.3. Формула Остроградского-Гаусса. Под замкнутой поверхностью будем понимать поверхность, являющуюся границей некоторой ограниченной пространственной области _V. Можно показать, что всякая кусочно-гладкая замкнутая поверхность является ориентированной. При этом ориентация определяется единичным вектором нормали к поверхности. Направление от поверхности внутрь области это внутренняя нормаль, соответственно наружу областиV - это внешняя нормаль.

Теорема 14. Если векторная функция ,непрерывна вместе с частными производными,,в областиV, то имеет место формула Остроградского-Гаусса

. (27)

Поверхностный интеграл берётся по внешней нормали

 Докажем эту формулу в случае, когда область является простой относительно осиOz. Представим, где, . Положительной ориентациейиявляются их положительные стороныис внешними нормалями (рис. 34).

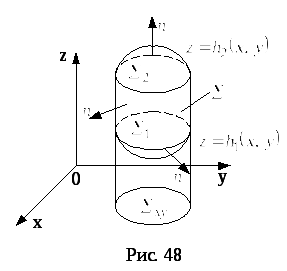
Преобразуем тройной интеграл по отк двойному интегралу по проекции

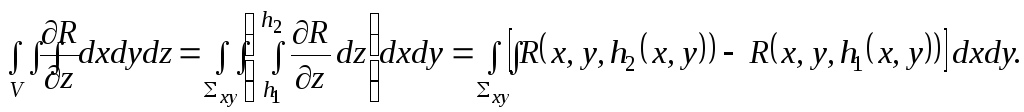
Двойные интегралы выразим через поверхностные, учитывая ориентацию поверхности:

,

,

тогда

.

Цилиндрическая поверхность имеет образующие параллельные осиOz, поэтому нормаль перпендикулярна образующей и, .

.

тогда

.

Аналогично, для областей простых относительно Оy и Оx получим формулы

,

.

Если область простая одновременно относительно всех координатных осей, то, складывая почленно последние три формулы, получаем (27).<

Формула Остроградского-Гаусса справедлива и для простой области. Пусть , где - простые области относительно какой-либо оси координат. Запишем для каждой формулу

и сложим полученные результаты. Тогда слева, в силу свойства адитивности тройного интеграла, получим интеграл по области . Далее, учитывая, что внешние нормали к внутренним частям границ области направлены в разные стороны, получаем, что сумма поверхностных интегралов по этим частям границ областей будет равна нулю. Следовательно, в правой части останутся только интегралы по тем частям границ , которые составляют в совокупность границу S области . В силу аддитивности поверхностного интеграла это будет интеграл по. Такое разбиение удобно проводить плоскостями параллельными осям координат.

Формула Остроградского-Гаусса справедлива, если функция непрерывна в, а,,непрерывны вV и тройной интеграл существует. А также, формула Остроградского-Гаусса справедлива и для многосвязной области, граница которой состоит из конечного числа кусочно-гладких поверхностей. В этом случае .

Пример 15. Пользуясь формулой Остроградского-Гаусса вычислить интеграл , где– внешняя сторона сферы.

Решение. По формуле Остроградского-Гаусса имеем

,

где – шар. Для вычисления интеграла перейдем к сферическим координатам,,,,. Якобиан перехода равен. Уравнение границы областиимеет вид. Получаем

.