
Механика.Методика решения задач
.pdf
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
61 |
||||||||||
ȼɵɪɚɠɟɧɢɟ (2.54) ɩɨɡɜɨɥɹɟɬ ɨɩɪɟɞɟɥɢɬɶ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ t0 , |
|||||||||||
ɜ ɤɨɬɨɪɵɣ ɛɪɭɫɨɤ ɧɚɱɢɧɚɟɬ ɫɤɨɥɶɡɢɬɶ ɩɨ ɞɨɫɤɟ: |
|
||||||||||
t0 |
Pmg M m |
. |
|
|
|
|
|
|
(2.55) |
||
MD |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ɂɬɚɤ: |
|
|
|
|
Dt |
|
|
|
|
|
|
°ɩɪɢ t d t0 : |
a |
A |
|
|
, |
|
|
|
|||
|
|
|
|
|
|
||||||
® |
|
|
|
|
|
M m |
|
|
(2.56) |
||
|
|
|
Dt Pmg |
|
|
Pmg |
|
||||
°°ɩɪɢ t ! t0 : |
a |
ɢ A |
. |
|
|||||||
|
m |
|
|
||||||||
¯ |
|
|
|
|
|
|
M |
|
|||
ɂɫɩɨɥɶɡɭɹ ɩɨɥɭɱɟɧɧɵɟ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɭɫɤɨɪɟɧɢɣ ɬɟɥ ɫɢɫɬɟ- |
|||||||||||
ɦɵ, ɨɩɪɟɞɟɥɢɦ ɬɟɩɟɪɶ ɡɚɤɨɧɵ ɢɡɦɟɧɟɧɢɹ ɫɤɨɪɨɫɬɟɣ ɷɬɢɯ ɬɟɥ. |
|
||||||||||
ɉɪɢ |
t d t0 ɫɤɨɪɨɫɬɢ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ ɦɟɧɹɸɬɫɹ ɨɞɢɧɚɤɨɜɵɦ |
||||||||||
ɨɛɪɚɡɨɦ ɢ ɤ ɦɨɦɟɧɬɭ ɜɪɟɦɟɧɢ t ɛɭɞɭɬ ɪɚɜɧɵ:
|
|
|
t |
|
t |
|
Dt |
|
|
|
|
|
Dt 2 |
|
|
|
|
|
|
||||
X |
V ³a d t |
|
³ |
|
|
|
d t |
|
|
|
|
. |
|
|
|
(2.57) |
|||||||
|
M m |
2 M m |
|
|
|
||||||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ɉɪɢ t ! t0 ɫɤɨɪɨɫɬɶ ɛɪɭɫɤɚ ɛɭɞɟɬ ɪɚɜɧɚ |
|
|
|
||||||||||||||||||||
|
|
|
Dt02 |
|
t |
Dt Pmg |
|
|
|
|
|
|
|
|
|
|
|||||||
X |
|
|
|
|
|
³ |
|
m |
|
|
|
d t , |
|
|
|
|
|
|
|||||
|
2 M m |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dt02 |
|
D t 2 t02 |
Pg t t0 , |
|
|
|
|
|
(2.58) |
|||||||||||
|
|
|
2 M m |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɚ ɫɤɨɪɨɫɬɶ ɞɨɫɤɢ – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Dt02 |
|
t |
|
Pmg |
|
|
|
|
|
Dt02 |
|
|
Pmg |
t t0 |
. |
|
||||
V |
|
|
|
|
|
|
³ |
|
|
|
d t |
|
|
|
|
|
|
|
(2.59) |
||||
|
|
2 M m |
|
M |
|
|
2 M m |
M |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X,V |
X |
|
|
|
|
|
|
|
|
|
|
X,V |
V |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
t0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Ɋɢɫ. 2.8 |
|
|
|
|
||||||
62 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
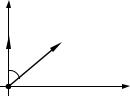
ɇɚ ɪɢɫ. 2.8 ɢɡɨɛɪɚɠɟɧɵ ɩɨɥɭɱɟɧɧɵɟ ɡɚɜɢɫɢɦɨɫɬɢ ɫɤɨɪɨɫɬɟɣ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ ɨɬ ɜɪɟɦɟɧɢ.
Ɂɚɞɚɱɚ 2.5
(ɉɪɹɦɚɹ ɡɚɞɚɱɚ ɞɢɧɚɦɢɤɢ)
ɇɚɣɬɢ ɡɚɤɨɧ ɞɜɢɠɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ, ɞɜɢɠɭɳɟɣɫɹ ɜ ɨɞɧɨɪɨɞɧɨɦ ɢ ɩɨɫɬɨɹɧɧɨɦ ɫɢɥɨɜɨɦ ɩɨɥɟ ɫ ɧɚɱɚɥɶɧɨɣ ɫɤɨɪɨɫɬɶɸ X0, ɧɚɩɪɚɜɥɟɧɧɨɣ ɩɨɞ ɩɪɨɢɡɜɨɥɶɧɵɦ ɭɝɥɨɦ D ɤ ɫɢɥɟ F.
|
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
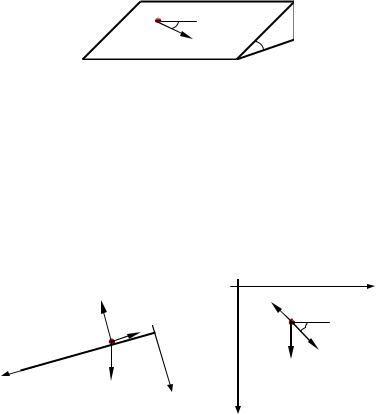
I. ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, |
Y |
|
|||||||
ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.9, ɩɪɢ ɷɬɨɦ ɧɚɱɚɥɨ |
|
|
|||||||
ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ ɫɨɜɩɚɞɚɟɬ ɫ ɩɨɥɨɠɟ- |
F |
X0 |
|||||||
ɧɢɟɦ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɧɚɱɚɥɶɧɵɣ |
|||||||||
|
|||||||||
ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ. |
|
D |
|||||||
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ |
O |
X |
|||||||
ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɨɫɢ |
|
Ɋɢɫ. 2.9 |
|||||||
ɜɵɛɪɚɧɧɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ: |
|
||||||||
|
|
||||||||
m |
dXx |
0 , |
|
|
|
(2.60) |
|||
d t |
|
|
|
||||||
m |
|
dXy |
|
F . |
|
(2.61) |
|||
|
d t |
|
|
||||||
III. ɉɪɨɢɧɬɟɝɪɢɪɭɟɦ ɭɪɚɜɧɟɧɢɹ (2.60) ɢ (2.61), ɢɫɩɨɥɶɡɭɹ ɧɚ- |
|||||||||
ɱɚɥɶɧɵɟ ɡɧɚɱɟɧɢɹ ɫɤɨɪɨɫɬɢ Xx (0) X0 sinD ɢ Xy (0) X0 cosD : |
|||||||||
Xx (t) |
|
X0 sin D , |
|
(2.62) |
|||||
Xy (t) |
|
X0 cosD |
F |
t . |
|
(2.63) |
|||
|
|
|
|||||||
|
|
|
|
|
m |
|
|
||
ɂɧɬɟɝɪɢɪɭɹ ɭɪɚɜɧɟɧɢɹ (2.62) ɢ (2.63) |
ɫ ɭɱɟɬɨɦ ɧɚɱɚɥɶɧɵɯ |
||||||||
ɡɧɚɱɟɧɢɣ ɤɨɨɪɞɢɧɚɬ x0 = 0 ɢ y0 = 0, ɩɨɥɭɱɚɟɦ ɡɚɤɨɧ ɞɜɢɠɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɤɨɨɪɞɢɧɚɬɧɨɣ ɮɨɪɦɟ:
x(t) |
X0 sin D t , |
|
|
(2.64) |
y(t) |
X0 cosD t |
Ft 2 |
|
|
|
. |
(2.65) |
||
|
||||
|
|
2m |
|
|
ɂɫɤɥɸɱɢɜ ɜɪɟɦɹ ɢɡ ɭɪɚɜɧɟɧɢɣ (2.64) ɢ (2.65), ɩɨɥɭɱɢɦ ɭɪɚɜɧɟɧɢɟ ɬɪɚɟɤɬɨɪɢɢ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ – ɭɪɚɜɧɟɧɢɟ ɩɚɪɚɛɨɥɵ:
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
63 |
|||
y |
F |
x2 ctgD x |
(2.66) |
|
2m(X0 sin D)2 |
||||
|
|
|
||
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜ ɨɞɧɨɪɨɞɧɨɦ ɫɢɥɨɜɨɦ ɩɨɥɟ ɦɚɬɟɪɢɚɥɶɧɚɹ ɬɨɱɤɚ ɞɜɢɠɟɬɫɹ ɩɨ ɩɚɪɚɛɨɥɟ.
Ɂɚɞɚɱɚ 2.6
Ɍɟɥɨ ɧɟɛɨɥɶɲɢɯ ɪɚɡɦɟɪɨɜ ɞɜɢɠɟɬɫɹ ɩɨ ɩɨɜɟɪɯɧɨɫɬɢ ɧɟɩɨɞɜɢɠɧɨɝɨ ɤɥɢɧɚ ɫ ɭɝɥɨɦ ɩɪɢ ɨɫɧɨɜɚɧɢɢ D . ȼ ɧɚɱɚɥɶɧɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɫɤɨɪɨɫɬɶ ɬɟɥɚ ɪɚɜɧɹɥɚɫɶ ȣ0 ɢ ɫɨɫɬɚɜɥɹɥɚ ɭɝɨɥ M0 ɫ ɪɟɛɪɨɦ ɤɥɢɧɚ (ɫɦ. ɪɢɫ. 2.10).
M0 |
D |
|
X0 |
||
|
Ɋɢɫ. 2.10
Ʉɨɷɮɮɢɰɢɟɧɬ ɬɪɟɧɢɹ ɬɟɥɚ ɨ ɩɨɜɟɪɯɧɨɫɬɶ ɤɥɢɧɚ P tgD . ɇɚɣɬɢ ɭɫɬɚɧɨɜɢɜɲɭɸɫɹ ɫɤɨɪɨɫɬɶ ɫɤɨɥɶɠɟɧɢɹ ɬɟɥɚ.
Ɋɟɲɟɧɢɟ
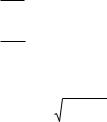
I. ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.11 (ɜɢɞ ɫɛɨɤɭ) ɢ ɪɢɫ. 2.12 (ɜɢɞ ɫɜɟɪɯɭ ɧɚ ɩɨɜɟɪɯɧɨɫɬɶ ɤɥɢɧɚ). Ɉɫɶ X ɧɚɩɪɚɜɢɦ ɜɞɨɥɶ ɧɚɤɥɨɧɧɨɣ ɩɥɨɫɤɨɫɬɢ ɩɚɪɚɥɥɟɥɶɧɨ ɪɟɛɪɭ ɤɥɢɧɚ (ɪɢɫ. 2.12). ɉɪɢ ɷɬɨɦ ɨɫɶ Y ɧɚɩɪɚɜɢɦ ɩɨ ɧɚɤɥɨɧɧɨɣ ɩɥɨɫɤɨɫɬɢ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɪɟɛɪɭ ɤɥɢɧɚ, ɚ ɨɫɶ Z ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɧɚɤɥɨɧɧɨɣ ɩɨɜɟɪɯɧɨɫɬɢ ɤɥɢɧɚ (ɪɢɫ. 2.11).
|
N |
Fɬɪ |
Fɬɪ |
|
X |
|
|
|
|
(t) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
mgsinD |
X(t) |
|
Y |
mg |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
Ɋɢɫ. 2.11 |
|
|
Ɋɢɫ. 2.12 |
||
64 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
ɇɚ ɪɢɫ. 2.11 ɢ 2.12 ɢɡɨɛɪɚɠɟɧɵ ɬɚɤɠɟ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɨ ɜ ɩɪɨɰɟɫɫɟ ɞɜɢɠɟɧɢɹ: ɫɢɥɚ ɬɹɠɟɫɬɢ mg, ɫɢɥɚ ɧɨɪɦɚɥɶɧɨɣ ɪɟɚɤɰɢɢ ɨɩɨɪɵ N ɢ ɫɢɥɚ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ Fɬɪ.
ɋɤɨɪɨɫɬɶ ɬɟɥɚ X(t) ɫɨɫɬɚɜɥɹɟɬ ɫ ɨɫɶɸ X ɭɝɨɥ ij(t) (ɫɦ. ɪɢɫ. 2.12), ɤɨɬɨɪɵɣ ɹɜɥɹɟɬɫɹ ɮɭɧɤɰɢɟɣ ɜɪɟɦɟɧɢ.
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɬɟɥɚ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɜɵɛɪɚɧɧɵɟ ɨɫɢ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ:
m |
dXx |
|
Fɬɪ cosM |
, |
(2.67) |
dt |
|
||||
|
|
|
|
|
|
m |
dXy |
|
mg sin D Fɬɪ sin M , |
(2.68) |
|
dt |
|
||||
|
|
|
|
|
|
0 |
N mg cosD . |
|
(2.69) |
||
ɂɫɩɨɥɶɡɭɟɦ ɡɚɤɨɧ Ⱥɦɨɧɬɨɧɚ – Ʉɭɥɨɧɚ (ɫɦ. ɩ. 2.1.2.ȼ) ɞɥɹ ɫɢɥɵ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ ɢ ɭɱɬɟɦ ɡɚɞɚɧɧɭɸ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ ɫɜɹɡɶ
ɤɨɷɮɮɢɰɢɟɧɬɚ ɬɪɟɧɢɹ |
P ɫ ɭɝɥɨɦ |
D ɩɪɢ ɨɫɧɨɜɚɧɢɢ ɧɚɤɥɨɧɧɨɣ |
|||||
ɩɥɨɫɤɨɫɬɢ: |
|
|
|
|
|
|
|
Fɬɪ |
PN tgD N . |
(2.70) |
|||||
Ɂɚɩɢɲɟɦ ɬɪɢɝɨɧɨɦɟɬɪɢɱɟɫɤɢɟ ɮɭɧɤɰɢɢ ɭɝɥɚ ij, ɜɵɪɚɡɢɜ ɢɯ |
|||||||
ɱɟɪɟɡ ɩɪɨɟɤɰɢɢ ɫɤɨɪɨɫɬɢ ɬɟɥɚ: |
|
||||||
cosM |
|
Xx |
, sin M |
|
Xy |
. |
(2.71) |
|
|
||||||
|
|
X |
|
X |
|
||
III. ɉɨɥɭɱɟɧɚ ɩɨɥɧɚɹ ɫɢɫɬɟɦɚ |
ɭɪɚɜɧɟɧɢɣ (2.67) – (2.71) ɞɥɹ |
||||||
ɨɩɪɟɞɟɥɟɧɢɹ ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɬɟɥɚ ɧɚ ɨɫɢ ɜɵɛɪɚɧɧɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ, ɪɟɲɢɬɶ ɤɨɬɨɪɭɸ ɜ ɨɛɳɟɦ ɜɢɞɟ ɞɨɫɬɚɬɨɱɧɨ ɫɥɨɠɧɨ ɢɡ-ɡɚ ɧɚɥɢɱɢɹ ɜ ɧɟɣ ɞɜɭɯ ɫɜɹɡɚɧɧɵɯ ɧɟɥɢɧɟɣɧɵɯ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɯ ɭɪɚɜɧɟɧɢɣ. Ɉɞɧɚɤɨ ɧɟɬ ɧɟɨɛɯɨɞɢɦɨɫɬɢ ɧɚɯɨɞɢɬɶ ɡɚɤɨɧ ɢɡɦɟɧɟɧɢɹ ɫɤɨɪɨɫɬɢ ɬɟɥɚ. ɉɨ ɭɫɥɨɜɢɸ ɡɚɞɚɱɢ ɬɪɟɛɭɟɬɫɹ ɨɩɪɟɞɟɥɢɬɶ ɭɫɬɚɧɨɜɢɜɲɭɸɫɹ ɫɤɨɪɨɫɬɶ ɬɟɥɚ, ɬ.ɟ. ɡɧɚɱɟɧɢɟ ɫɤɨɪɨɫɬɢ ɜ ɬɨ ɜɪɟɦɹ, ɤɨɝɞɚ ɫɭɦɦɚ ɫɢɥ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɬɟɥɨ, ɫɬɚɧɟɬ ɪɚɜɧɨɣ ɧɭɥɸ.
Ɋɚɫɫɦɨɬɪɢɦ ɢɡɦɟɧɟɧɢɟ ɯɚɪɚɤɬɟɪɚ ɞɜɢɠɟɧɢɹ ɬɟɥɚ ɫɨ ɜɪɟɦɟɧɟɦ. ȼ ɩɥɨɫɤɨɫɬɢ ɞɜɢɠɟɧɢɹ ɧɚ ɬɟɥɨ ɞɟɣɫɬɜɭɸɬ ɞɜɟ ɫɢɥɵ: ɫɢɥɚ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ ɢ ɩɪɨɟɤɰɢɹ ɫɢɥɵ ɬɹɠɟɫɬɢ. ɂɡ (2.69) ɢ (2.70) ɩɨɥɭ-
ɱɢɦ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɫɢɥɵ ɬɪɟɧɢɹ: |
|
Fɬɪ mg sin D . |
(2.77) |
Ʉɚɤ ɜɢɞɢɦ, ɦɨɞɭɥɶ ɫɢɥɵ ɬɪɟɧɢɹ ɪɚɜɟɧ ɜɟɥɢɱɢɧɟ ɩɪɨɟɤɰɢɢ ɫɢɥɵ ɬɹɠɟɫɬɢ ɧɚ ɧɚɤɥɨɧɧɭɸ ɩɥɨɫɤɨɫɬɶ. Ⱦɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɨ ɫɢɥɵ ɛɭ-
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
65 |
ɞɭɬ ɩɨɜɨɪɚɱɢɜɚɬɶ ɜɟɤɬɨɪ ɫɤɨɪɨɫɬɢ ɬɟɥɚ ɞɨ ɬɟɯ ɩɨɪ, ɩɨɤɚ ɨɧ ɧɟ ɫɨɜɩɚɞɟɬ ɩɨ ɧɚɩɪɚɜɥɟɧɢɸ ɫ ɨɫɶɸ Y. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɭɫɤɨɪɟɧɢɟ ɨɛɪɚɬɢɬɫɹ ɜ ɧɨɥɶ, ɤɨɝɞɚ ɫɢɥɚ ɬɪɟɧɢɹ ɛɭɞɟɬ ɧɚɩɪɚɜɥɟɧɚ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨ ɫɨɫɬɚɜɥɹɸɳɟɣ ɫɢɥɵ ɬɹɠɟɫɬɢ ɜ ɩɥɨɫɤɨɫɬɢ ɞɜɢɠɟɧɢɹ ɬɟɥɚ. Ⱦɚɥɶɧɟɣɲɟɟ ɞɜɢɠɟɧɢɟ ɛɭɞɟɬ ɩɪɨɢɫɯɨɞɢɬɶ ɫ ɩɨɫɬɨɹɧɧɨɣ ɫɤɨɪɨɫɬɶɸ Xɭɫɬ, ɧɚɩɪɚɜɥɟɧɧɨɣ ɜɞɨɥɶ ɨɫɢ Y.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɞɨɫɬɚɬɨɱɧɨ ɧɚɣɬɢ ɭɪɚɜɧɟɧɢɟ, ɫɜɹɡɵɜɚɸɳɟɟ ɩɪɨɟɤɰɢɸ ɫɤɨɪɨɫɬɢ ɬɟɥɚ ɧɚ ɨɫɶ Y ɫ ɦɨɞɭɥɟɦ ɟɝɨ ɫɤɨɪɨɫɬɢ. Ⱦɥɹ ɷɬɨɝɨ ɩɪɟɨɛɪɚɡɭɟɦ ɩɨɥɭɱɟɧɧɭɸ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ (2.67) – (2.71) ɤ ɜɢɞɭ:
dXx
dt dXy
dt
XXx g sin D ,
§ |
|
X |
y |
· |
|
¨ |
|
|
|
¸ |
|
¨1 |
|
X |
¸g sin D . |
||
© |
|
|
¹ |
||
(2.72)
(2.73)
ɉɪɨɢɡɜɨɞɧɭɸ ɨɬ ɦɨɞɭɥɹ ɫɤɨɪɨɫɬɢ ɩɨ ɜɪɟɦɟɧɢ ɩɪɟɞɫɬɚɜɢɦ ɜ ɜɢɞɟ:
|
dX |
|
d |
Xx2 Xy2 |
Xx |
|
dXx |
|
Xy |
|
dXy |
. |
(2.74) |
||
|
dt |
|
dt |
dt |
|
|
|||||||||
|
|
|
|
X |
|
|
X dt |
|
|||||||
ɉɨɞɫɬɚɧɨɜɤɚ (2.72) ɢ (2.73) ɜ (2.74) ɩɪɢɜɨɞɢɬ ɤ ɭɪɚɜɧɟɧɢɸ: |
|||||||||||||||
|
dX |
|
dXy |
. |
|
|
|
|
|
|
|
|
(2.75) |
||
|
dt |
|
dt |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ɭɫɥɨɜɢɣ (X(0) X0 , |
||
ɂɧɬɟɝɪɢɪɭɹ |
|
(2.75) ɫ |
ɭɱɟɬɨɦ |
ɧɚɱɚɥɶɧɵɯ |
|||||||||||
M(0) M0 ), ɩɨɥɭɱɚɟɦ: |
|
|
|
|
|
|
|
|
|
||||||
X |
Xy |
|
X0 (1 sin M0 ) . |
|
|
|
|
|
|
|
(2.76) |
||||
ɉɨɞɫɬɚɜɥɹɹ X = Xy = Xɭɫɬ ɜ (2.76), ɧɚɯɨɞɢɦ ɢɫɤɨɦɵɣ ɦɨɞɭɥɶ ɫɤɨɪɨɫɬɢ ɭɫɬɚɧɨɜɢɜɲɟɝɨɫɹ ɞɜɢɠɟɧɢɹ:
Xɭɫɬ |
|
X0 |
(1 sin M0 ) . |
(2.78) |
|
2 |
|||||
|
|
|
|||
ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɩɨɥɭɱɟɧɧɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɭɫɬɚɧɨɜɢɜɲɟɣɫɹ ɫɤɨɪɨɫɬɢ ɜ ɞɜɭɯ ɱɚɫɬɧɵɯ ɫɥɭɱɚɹɯ.
ȿɫɥɢ ij0 = ʌ/2 (ɧɚɱɚɥɶɧɚɹ ɫɤɨɪɨɫɬɶ ɬɟɥɚ ɧɚɩɪɚɜɥɟɧɚ ɜɧɢɡ ɩɨ ɧɚɤɥɨɧɧɨɣ ɩɥɨɫɤɨɫɬɢ), ɬɨ Xɭɫɬ = X0. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɞɜɢɠɟɧɢɟ ɬɟɥɚ ɫɪɚɡɭ ɩɪɨɢɫɯɨɞɢɬ ɫ ɩɨɫɬɨɹɧɧɨɣ ɫɤɨɪɨɫɬɶɸ, ɩɨɫɤɨɥɶɤɭ ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɧɟɝɨ ɫɢɥɵ ɫɤɨɦɩɟɧɫɢɪɨɜɚɧɵ.
66 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
|
ɉɪɢ ij0 = –ʌ/2 |
ɫɤɨɪɨɫɬɶ |
ɭɫɬɚɧɨɜɢɜɲɟɝɨɫɹ ɞɜɢɠɟɧɢɹ ɪɚɜɧɚ |
Xɭɫɬ = 0. ɇɚɱɚɥɶɧɚɹ |
ɫɤɨɪɨɫɬɶ, |
ɧɚɩɪɚɜɥɟɧɧɚɹ ɜɜɟɪɯ ɩɨ ɧɚɤɥɨɧɧɨɣ |
ɩɥɨɫɤɨɫɬɢ, ɩɪɢɜɨɞɢɬ ɤ ɪɚɜɧɨɡɚɦɟɞɥɟɧɧɨɦɭ ɞɜɢɠɟɧɢɸ. ɉɪɢ ɷɬɨɦ ɢ ɩɪɨɟɤɰɢɹ ɫɢɥɵ ɬɹɠɟɫɬɢ, ɢ ɫɢɥɚ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ ɧɚɩɪɚɜɥɟɧɵ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨ ɫɤɨɪɨɫɬɢ. ɑɟɪɟɡ ɧɟɤɨɬɨɪɨɟ ɜɪɟɦɹ ɫɤɨɪɨɫɬɶ ɬɟɥɚ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɨɥɶ. ɋɢɥɚ ɬɪɟɧɢɹ ɫɬɚɧɨɜɢɬɫɹ ɫɢɥɨɣ ɬɪɟɧɢɹ ɩɨɤɨɹ ɢ ɦɟɧɹɟɬ ɧɚɩɪɚɜɥɟɧɢɟ ɧɚ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɟ. Ⱦɜɢɠɟɧɢɹ ɜɧɢɡ ɩɨ ɧɚɤɥɨɧɧɨɣ ɩɥɨɫɤɨɫɬɢ ɧɟ ɩɪɨɢɫɯɨɞɢɬ, ɬ.ɤ. ɦɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɫɢɥɵ ɬɪɟɧɢɹ ɩɨɤɨɹ ɜ ɭɫɥɨɜɢɹɯ ɞɚɧɧɨɣ ɡɚɞɚɱɢ ɫɨɜɩɚɞɚɟɬ ɩɨ ɦɨɞɭɥɸ ɫɨ ɡɧɚɱɟɧɢɟɦ ɩɪɨɟɤɰɢɢ ɫɢɥɵ ɬɹɠɟɫɬɢ ɧɚ ɧɚɤɥɨɧɧɭɸ ɩɥɨɫɤɨɫɬɶ.
Ɂɚɞɚɱɚ 2.7
ɋɬɚɥɶɧɨɣ ɲɚɪɢɤ ɪɚɞɢɭɫɚ r ɧɚɱɢɧɚɟɬ ɞɜɢɝɚɬɶɫɹ ɜ ɫɨɫɭɞɟ, ɡɚɩɨɥɧɟɧɧɨɦ ɝɥɢɰɟɪɢɧɨɦ, ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɫɢɥɵ ɬɹɠɟɫɬɢ. ɇɚɣɬɢ ɡɚɜɢɫɢɦɨɫɬɶ ɫɤɨɪɨɫɬɢ ɲɚɪɢɤɚ ɨɬ ɜɪɟɦɟɧɢ X(t), ɚ ɬɚɤɠɟ ɨɩɪɟɞɟɥɢɬɶ ɫɤɨɪɨɫɬɶ ɭɫɬɚɧɨɜɢɜɲɟɝɨɫɹ ɞɜɢɠɟɧɢɹ ɲɚɪɢɤɚ Xɭɫɬ. Ʉɨɷɮɮɢɰɢɟɧɬ ɜɹɡɤɨɝɨ ɬɪɟɧɢɹ ɜ ɝɥɢɰɟɪɢɧɟ ɪɚɜɟɧ K, ɩɥɨɬɧɨɫɬɶ ɝɥɢɰɟɪɢɧɚ – U1, ɩɥɨɬɧɨɫɬɶ ɫɬɚɥɢ – U2. ɋɱɢɬɚɬɶ, ɱɬɨ ɫɢɥɚ ɜɹɡɤɨɝɨ ɬɪɟɧɢɹ ɨɩɪɟɞɟɥɹɟɬɫɹ ɮɨɪɦɭɥɨɣ ɋɬɨɤɫɚ: Fɜ = 6SrXK .
Ɋɟɲɟɧɢɟ
I. ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ, ɫɜɹɡɚɧɧɭɸ ɫ ɫɨɫɭɞɨɦ, ɬɚɤ, ɤɚɤ
ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.13. ɇɚɱɚɥɨ ɤɨɨɪɞɢɧɚɬ ɫɨ- |
|
|
||||
ɜɦɟɫɬɢɦ ɫ ɩɨɥɨɠɟɧɢɟɦ ɲɚɪɢɤɚ ɜ ɦɨɦɟɧɬ ɧɚ- |
FȺ |
Y |
||||
ɱɚɥɚ ɟɝɨ ɞɜɢɠɟɧɢɹ. ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɫɥɨɜɢ- |
||||||
Fɜ |
|
|||||
ɟɦ ɡɚɞɚɱɢ ɧɚɱɚɥɶɧɚɹ ɫɤɨɪɨɫɬɶ ɲɚɪɢɤɚ ɪɚɜɧɚ |
|
|
||||
ɧɭɥɸ: X 0 |
0 . |
|
|
|
||
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɲɚɪɢ- |
mg |
|
||||
ɤɚ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɨɫɶ X ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ: |
|
|||||
|
|
|||||
ma |
|
mg Fɜ FA , |
(2.79) |
X |
|
|
ɝɞɟ Fɜ – ɫɢɥɚ ɜɹɡɤɨɝɨ ɬɪɟɧɢɹ, ɚ FA |
– ɫɢɥɚ |
Ɋɢɫ. 2.13 |
||||
Ⱥɪɯɢɦɟɞɚ. |
|
|
|
|
|
|
ɂɫɩɨɥɶɡɭɟɦ ɡɚɤɨɧ Ⱥɪɯɢɦɟɞɚ ɢ ɮɨɪɦɭɥɭ ɋɬɨɤɫɚ, ɨɩɢɫɵɜɚɸ- |
||||||
ɳɢɟ ɫɜɨɣɫɬɜɚ ɷɬɢɯ ɫɢɥ: |
|
|
|
|||
FA |
|
U1gV , |
|
|
(2.80) |
|
Fɜ |
6SrXK . |
|
|
(2.81) |
||

Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
67 |
|||||||||||||||||
Ɂɞɟɫɶ V |
|
|
4 |
Sr3 |
|
– ɨɛɴɟɦ ɲɚɪɢɤɚ. |
|
|
||||||||||
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ȼɵɪɚɡɢɦ ɬɚɤɠɟ ɦɚɫɫɭ ɲɚɪɢɤɚ ɱɟɪɟɡ ɟɝɨ ɩɥɨɬɧɨɫɬɶ: |
|
|||||||||||||||||
m U2V . |
|
|
|
|
|
|
|
|
(2.82) |
|||||||||
III. ɉɨɞɫɬɚɜɥɹɹ (2.80) – (2.82) ɜ ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ (2.79), |
||||||||||||||||||
ɩɨɥɭɱɚɟɦ: |
|
|
|
|
|
|
|
|
|
|||||||||
|
U V |
dX |
|
U |
2 |
U Vg 6SrXK . |
|
(2.83) |
||||||||||
|
|
|
|
|
||||||||||||||
2 |
|
|
dt |
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ⱦɥɹ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ (2.83) ɩɪɢɜɟɞɟɦ ɟɝɨ ɤ ɜɢɞɭ |
|
|||||||||||||||||
|
dX |
|
|
|
|
U2 U1 |
|
g |
6SrK |
X A BX |
|
(2.84) |
||||||
|
dt |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
U |
2 |
|
|
|
U V |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
ɢ ɫɞɟɥɚɟɦ ɡɚɦɟɧɭ ɩɟɪɟɦɟɧɧɵɯ: |
|
|
||||||||||||||||
|
A BX |
z . |
|
|
|
|
|
|
(2.85) |
|||||||||
Ⱦɢɮɮɟɪɟɧɰɢɪɭɹ (2.85) ɩɨ ɜɪɟɦɟɧɢ, ɩɨɥɭɱɚɟɦ: |
|
|||||||||||||||||
B |
dX |
|
d z |
. |
|
|
|
|
|
(2.86) |
||||||||
d t |
|
|
|
|
|
|
||||||||||||
|
|
|
d t |
|
|
|
|
|
|
|
||||||||
ɋ ɭɱɟɬɨɦ (2.86) ɜɵɪɚɠɟɧɢɟ (2.84) ɩɪɢɧɢɦɚɟɬ ɫɥɟɞɭɸɳɢɣ ɜɢɞ: |
|
|||||||||||||||||
|
d z |
|
|
Bz . |
|
|
|
|
|
|
(2.87) |
|||||||
|
d t |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɟɲɢɦ ɩɨɥɭɱɟɧɧɨɟ ɭɪɚɜɧɟɧɢɟ ɦɟɬɨɞɨɦ ɪɚɡɞɟɥɟɧɢɹ ɩɟɪɟɦɟɧ- |
||||||||||||||||||
ɧɵɯ ɫ ɭɱɟɬɨɦ ɧɚɱɚɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ ɫɤɨɪɨɫɬɢ X 0 |
0 : |
|
||||||||||||||||
|
z Ae Bt . |
|
|
|
|
|
|
|
(2.88) |
|||||||||
ɂɫɩɨɥɶɡɭɹ ɮɨɪɦɭɥɭ (2.85), ɜɟɪɧɟɦɫɹ ɤ ɫɬɚɪɨɣ ɩɟɪɟɦɟɧɧɨɣ X: |
||||||||||||||||||
X |
|
A |
1 e Bt . |
|
(2.89) |
|||||||||||||
|
|
|
||||||||||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
||||||
ɉɨɞɫɬɚɜɢɜ ɡɧɚɱɟɧɢɹ ɤɨɧɫɬɚɧɬ A ɢ B ɢɡ (2.84), ɚ ɬɚɤɠɟ ɡɧɚɱɟɧɢɟ V, ɩɨɥɭɱɢɦ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɫɤɨɪɨɫɬɢ ɲɚɪɢɤɚ:
|
U |
|
U g |
2r |
2 |
§ |
§ |
|
9K |
·· |
|
||
X |
2 |
|
¨1 |
exp¨ |
|
t ¸¸ . |
(2.90) |
||||||
|
|
|
2 |
|
|||||||||
|
|
1 |
9K |
¨ |
¨ |
|
2r |
U2 |
¸¸ |
|
|||
|
|
|
|
© |
© |
|
|
¹¹ |
|
||||
ɉɪɢ t !! 2r 2 U2 ɫɤɨɪɨɫɬɶ ɞɜɢɠɟɧɢɹ ɲɚɪɢɤɚ ɩɪɚɤɬɢɱɟɫɤɢ ɧɟ
9K
ɢɡɦɟɧɹɟɬɫɹ ɢ ɪɚɜɧɚ
X |
ɭɫɬ |
U |
2 |
U g |
2r 2 |
. |
(2.91) |
|
|||||||
|
|
1 |
9K |
|
|||
|
|
|
|
|
|
||
68 ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ
Ɂɚɞɚɱɚ 2.8
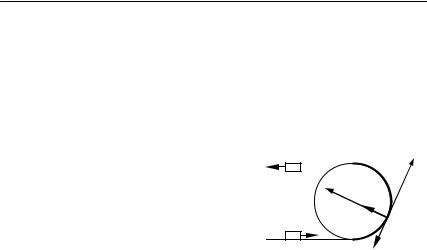
Ȼɪɭɫɨɤ ɫɤɨɥɶɡɢɬ ɩɨ ɝɥɚɞɤɨɣ ɝɨɪɢɡɨɧɬɚɥɶɧɨɣ ɩɨɜɟɪɯɧɨɫɬɢ ɫɨ ɫɤɨɪɨɫɬɶɸ ȣ0 ɢ ɩɨ ɤɚɫɚɬɟɥɶɧɨɣ ɩɨɩɚɞɚɟɬ ɜ ɨɛɥɚɫɬɶ, ɨɝɪɚɧɢɱɟɧɧɭɸ
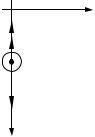
ɡɚɛɨɪɨɦ ɜ ɮɨɪɦɟ ɩɨɥɭɨɤɪɭɠɧɨɫɬɢ (ɪɢɫ. 2.14). Ɉɩɪɟɞɟɥɢɬɶ ɜɪɟɦɹ, ɱɟɪɟɡ ɤɨɬɨɪɨɟ ɛɪɭɫɨɤ ɩɨɤɢɧɟɬ ɷɬɭ ɨɛɥɚɫɬɶ. Ɋɚɞɢɭɫ ɤɪɢɜɢɡɧɵ ɡɚɛɨɪɚ R, ɤɨɷɮɮɢɰɢɟɧɬ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ ɛɪɭɫɤɚ ɨ ɩɨɜɟɪɯɧɨɫɬɶ ɡɚɛɨɪɚ P.
Ɋɚɡɦɟɪɵ ɛɪɭɫɤɚ ɦɧɨɝɨ ɦɟɧɶɲɟ R. |
|
|
|
|
Fɬɪ |
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
IJ |
I. ȼɵɛɟɪɟɦ ɩɪɨɢɡɜɨɥɶɧɭɸ ɢɧɟɪ- |
|
|
|
|
||
X |
|
|
|
|||
ɰɢɚɥɶɧɭɸ ɫɢɫɬɟɦɭ ɨɬɫɱɟɬɚ, ɠɟɫɬɤɨ |
|
n |
||||
|
|
|
||||
ɫɜɹɡɚɧɧɭɸ ɫ ɡɚɛɨɪɨɦ. ɂɡɨɛɪɚɡɢɦ ɧɚ |
|
|
|
|
|
|
ɪɢɫɭɧɤɟ |
ɬɚɧɝɟɧɰɢɚɥɶɧɭɸ ɨɫɶ, ɡɚɞɚɧ- |
|
|
|
X0 |
|
ɧɭɸ ɨɪɬɨɦ IJ , ɧɚɩɪɚɜɥɟɧɧɭɸ ɜɞɨɥɶ |
|
|
|
|||
|
|
|
|
Fɬɪ |
||
ɫɤɨɪɨɫɬɢ ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ, ɢ ɧɨɪ- |
|
|
|
|
||
ɦɚɥɶɧɭɸ ɨɫɶ, ɡɚɞɚɧɧɭɸ ɨɪɬɨɦ n , ɧɚ- |
|
|
|
Ɋɢɫ. 2.14 |
||
ɩɪɚɜɥɟɧɧɭɸ ɤ ɰɟɧɬɪɭ ɤɪɢɜɢɡɧɵ ɬɪɚ- |
|
|
|
|||
|
|
|
|
|
||
ɟɤɬɨɪɢɢ |
ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɫɤɨɪɨɫɬɢ |
|
|
|
|
|
(ɫɦ. ɬɟɨɪɟɬɢɱɟɫɤɢɣ ɦɚɬɟɪɢɚɥ ɜ Ƚɥɚɜɟ 1).
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ ɨɬɧɨɫɢɬɟɥɶɧɨ ɢɧɟɪɰɢɚɥɶɧɨɣ ɫɢɫɬɟɦɵ ɨɬɫɱɟɬɚ, ɠɟɫɬɤɨ ɫɜɹɡɚɧɧɨɣ ɫ ɡɚɛɨɪɨɦ, ɜ ɩɪɨɟɤɰɢ-
ɹɯ ɧɚ ɬɚɧɝɟɧɰɢɚɥɶɧɭɸ ɢ ɧɨɪɦɚɥɶɧɭɸ ɨɫɢ: |
|
|||||||||
ma |
m |
dX |
|
F , |
(2.95) |
|||||
|
|
|||||||||
|
W |
|
|
|
d t |
ɬɪ |
|
|||
|
|
|
|
|
|
|
|
|||
man |
m |
X2 |
N . |
(2.96) |
||||||
|
|
R |
||||||||
|
|
|
|
|
|
|
|
|
||
ȼɨɫɩɨɥɶɡɭɟɦɫɹ ɡɚɤɨɧɨɦ Ⱥɦɨɧɬɨɧɚ – Ʉɭɥɨɧɚ ɞɥɹ ɫɢɥɵ ɬɪɟɧɢɹ |
||||||||||
ɫɤɨɥɶɠɟɧɢɹ: |
|
|
|
|
|
|
||||
|
Fɬɪ |
PN . |
|
(2.97) |
||||||
III ɂɡ (2.95) – (2.97) ɩɨɥɭɱɢɦ ɭɪɚɜɧɟɧɢɟ ɞɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɦɨ- |
||||||||||
ɞɭɥɹ ɫɤɨɪɨɫɬɢ ɛɪɭɫɤɚ: |
|
|||||||||
|
dX |
P |
X2 |
|
|
|||||
|
|
|
. |
(2.98) |
||||||
|
d t |
|||||||||
|
|
|
|
|
R |
|
|
|||
Ɋɟɲɚɹ ɭɪɚɜɧɟɧɢɟ (2.98) ɦɟɬɨɞɨɦ ɪɚɡɞɟɥɟɧɢɹ ɩɟɪɟɦɟɧɧɵɯ, ɩɨ- |
||||||||||
ɥɭɱɢɦ: |
|
|
|
|
|
|
|
|
||
|
dX |
|
|
P |
d t |
, |
(2.99) |
|||
|
X2 |
|
||||||||
|
|
R |
|
|
||||||

Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
69 |
1 P t C .
X R
Ʉɨɧɫɬɚɧɬɭ ɋ
(X(0) X0 ): C |
1 |
. |
|
||
|
X0 |
|
(2.100)
ɜ (2.100) ɨɩɪɟɞɟɥɢɦ ɢɡ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɨɞɭɥɶ ɫɤɨɪɨɫɬɢ ɛɪɭɫɤɚ ɜ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ t, ɤɨɝɞɚ ɛɪɭɫɨɤ ɟɳɟ ɞɜɢɠɟɬɫɹ ɜɞɨɥɶ ɡɚɛɨɪɚ, ɨɩɪɟɞɟɥɹɟɬɫɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
X X0 |
|
1 |
|
. |
(2.101) |
|
PX0 |
|
|||
1 |
t |
|
|||
R |
|
||||
|
|
|
|
|
|
Ɂɚɦɟɬɢɦ, ɱɬɨ ɞɥɹ ɥɸɛɨɝɨ ɦɨɦɟɧɬɚ ɜɪɟɦɟɧɢ t ɢ ɩɪɢ ɥɸɛɨɣ, ɧɟ ɪɚɜɧɨɣ ɧɭɥɸ, ɧɚɱɚɥɶɧɨɣ ɫɤɨɪɨɫɬɢ X0, ɫɤɨɪɨɫɬɶ ɛɪɭɫɤɚ X > 0. ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɛɪɭɫɨɤ ɧɟ ɨɫɬɚɧɨɜɢɬɫɹ, ɚ ɨɛɹɡɚɬɟɥɶɧɨ ɩɪɨɣɞɟɬ ɜɫɸ ɨɛɥɚɫɬɶ, ɨɝɪɚɧɢɱɟɧɧɭɸ ɡɚɛɨɪɨɦ, ɩɨɫɤɨɥɶɤɭ ɫ ɭɦɟɧɶɲɟɧɢɟɦ ɫɤɨɪɨɫɬɢ ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ ɭɦɟɧɶɲɚɟɬɫɹ ɢ ɫɢɥɚ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ ɦɟɠɞɭ ɛɪɭɫɤɨɦ ɢ ɡɚɛɨɪɨɦ.
ɉɭɬɶ, ɩɪɨɣɞɟɧɧɵɣ ɬɟɥɨɦ ɡɚ ɜɪɟɦɹ d t |
ɫ ɦɨɦɟɧɬɚ ɜɪɟɦɟɧɢ t, |
|||||
ɩɪɢ ɞɜɢɠɟɧɢɢ ɜɞɨɥɶ ɡɚɛɨɪɚ, ɪɚɜɟɧ: |
|
|||||
d s X d t X0 |
|
1 |
|
d t . |
(2.102) |
|
1 |
PX0 |
t |
||||
|
|
|
R |
|
||
ɉɭɬɶ, ɩɪɨɣɞɟɧɧɵɣ ɬɟɥɨɦ ɡɚ ɜɪɟɦɹ t ɞɜɢɠɟɧɢɹ ɜɞɨɥɶ ɡɚɛɨɪɚ ɩɨɥɭɱɢɦ ɢɧɬɟɝɪɢɪɨɜɚɧɢɟɦ (2.102) ɩɨ ɜɪɟɦɟɧɢ:
s |
|
R |
|
|
§ |
|
|
|
|
PX |
0 |
t |
· |
|
||
|
|
|
ln¨1 |
|
|
¸ . |
(2.103) |
|||||||||
|
P |
|
R |
|
||||||||||||
|
|
|
|
© |
|
|
|
|
|
|
¹ |
|
||||
Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɜɪɟɦɟɧɢ, ɱɟɪɟɡ ɤɨɬɨɪɨɟ ɛɪɭɫɨɤ ɩɨɤɢɧɟɬ ɨɛ- |
||||||||||||||||
ɥɚɫɬɶ, ɨɝɪɚɧɢɱɟɧɧɭɸ ɡɚɛɨɪɨɦ ɩɪɟɨɛɪɚɡɭɟɦ (2.103) ɤ ɜɢɞɭ: |
|
|||||||||||||||
|
|
|
R |
|
§ |
P |
s |
|
· |
|
|
|||||
|
|
|
|
|
|
|
||||||||||
t |
|
|
|
|
|
¨e R |
1¸ . |
(2.104) |
||||||||
PX |
|
|||||||||||||||
|
0 |
¨ |
|
|
|
|
|
¸ |
|
|
||||||
|
|
|
|
|
© |
|
|
|
|
|
¹ |
|
|
|||
ɉɨɫɤɨɥɶɤɭ |
ɞɥɢɧɚ ɡɚɛɨɪɚ s SR ɢɫɤɨɦɨɟ ɜɪɟɦɹ |
ɞɜɢɠɟɧɢɹ |
||||||||||||||
ɛɪɭɫɤɚ ɜɞɨɥɶ ɡɚɛɨɪɚ t0 |
ɪɚɜɧɨ: |
|
||||||||||||||
t0 |
|
|
|
R |
|
|
eSP 1 . |
|
(2.105) |
|||||||
|
|
PX |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
70 ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ
ɉɪɢ ɦɚɥɵɯ ɡɧɚɱɟɧɢɹɯ ɤɨɷɮɮɢɰɢɟɧɬɚ ɬɪɟɧɢɹ ( SP 1 ) ɜɪɟɦɹ
ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ t0 ɛɭɞɟɬ ɪɚɜɧɨ |
|
|
|||||||
t0 |
R |
|
eSP 1 |
R |
|
(1 |
SP ...) 1 # SR . |
(2.106) |
|
PX |
|
PX |
|
||||||
|
0 |
|
0 |
|
X |
0 |
|
||
|
|
|
|
|
|
|
|||
Ɂɚɞɚɱɚ 2.9
ɇɚ ɫɬɨɥɟ ɥɟɠɢɬ ɞɨɫɤɚ ɦɚɫɫɨɣ Ɇ = 1 ɤɝ, ɚ ɧɚ ɞɨɫɤɟ – ɝɪɭɡ ɦɚɫɫɨɣ m = 2 ɤɝ. Ʉɚɤɭɸ ɫɢɥɭ F ɧɭɠɧɨ ɩɪɢɥɨɠɢɬɶ ɤ ɞɨɫɤɟ, ɱɬɨɛɵ ɨɧɚ ɜɵɫɤɨɥɶɡɧɭɥɚ ɢɡ-ɩɨɞ ɝɪɭɡɚ? Ʉɨɷɮɮɢɰɢɟɧɬ ɬɪɟɧɢɹ ɦɟɠɞɭ ɝɪɭɡɨɦ ɢ ɞɨɫɤɨɣ ɪɚɜɟɧ P1 = 0,25, ɚ ɦɟɠɞɭ ɞɨɫɤɨɣ ɢ ɫɬɨɥɨɦ – P2 = 0,5.
Ɋɟɲɟɧɢɟ
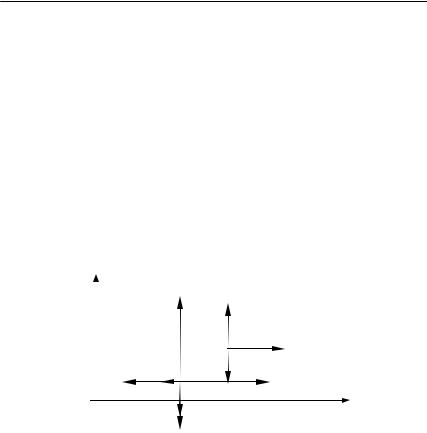
I.ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.15
ɢɢɡɨɛɪɚɡɢɦ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɚ ɫɢɫɬɟɦɵ.
Y
RN
|
|
|
|
|
Fɬɪ1 |
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Fɬɪ1 Fɬɪ |
|
mg |
F |
|||
|
|
|
|
|
|
|
|
|
N |
Mg |
|
|
|
X |
|
|
|
|
|
|
|
||
|
|
Ɋɢɫ. 2.15 |
|
|
|
|
|
ɇɚ ɝɪɭɡ ɜ ɩɪɨɰɟɫɫɟ ɞɜɢɠɟɧɢɹ ɞɟɣɫɬɜɭɸɬ ɫɢɥɚ ɬɹɠɟɫɬɢ mg, ɫɢɥɚ ɬɪɟɧɢɹ Fɬɪ1 ɢ ɫɢɥɚ ɧɨɪɦɚɥɶɧɨɣ ɪɟɚɤɰɢɢ ɞɨɫɤɢ N. Ʉ ɞɨɫɤɟ ɩɪɢ-
ɥɨɠɟɧɵ ɝɨɪɢɡɨɧɬɚɥɶɧɚɹ ɫɢɥɚ F, ɫɢɥɚ ɬɹɠɟɫɬɢ Mg, ɫɢɥɚ ɧɨɪɦɚɥɶɧɨɣ ɪɟɚɤɰɢɢ ɫɬɨɥɚ R, ɫɢɥɚ ɧɨɪɦɚɥɶɧɨɝɨ ɞɚɜɥɟɧɢɹ ɝɪɭɡɚ N ɢ ɫɢɥɵ ɬɪɟɧɢɹ ɫɨ ɫɬɨɪɨɧɵ ɝɪɭɡɚ ɢ ɫɬɨɥɚ Fɬɪ1 ɢ Fɬɪ2 . ɋɢɥɚɦɢ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜɨɡ-
ɞɭɯɚ ɩɪɟɧɟɛɪɟɝɚɟɦ.
ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɯɚɪɚɤɬɟɪ ɞɜɢɠɟɧɢɹ ɬɟɥ ɫɢɫɬɟɦɵ. ȿɫɥɢ ɩɪɢɥɨɠɟɧɧɚɹ ɤ ɞɨɫɤɟ ɫɢɥɚ F ɦɚɥɚ, ɬɨ ɝɪɭɡ ɢ ɞɨɫɤɚ ɞɜɢɠɭɬɫɹ ɫ ɨɞɢɧɚɤɨɜɵɦ ɭɫɤɨɪɟɧɢɟɦ (ɢɥɢ ɩɨɤɨɹɬɫɹ), ɚ ɫɢɥɚ ɬɪɟɧɢɹ Fɬɪ1 ɦɟɠɞɭ ɝɪɭɡɨɦ ɢ
ɞɨɫɤɨɣ ɹɜɥɹɟɬɫɹ ɫɢɥɨɣ ɬɪɟɧɢɹ ɩɨɤɨɹ. ɋ ɭɜɟɥɢɱɟɧɢɟɦ ɜɧɟɲɧɟɣ ɫɢɥɵ
