
Механика.Методика решения задач
.pdfȽɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
51 |
4) ɫɢɥɚ ɫɭɯɨɝɨ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ ɧɚɩɪɚɜɥɟɧɚ ɩɪɨɬɢɜɨɩɨɥɨɠ- |
|
ɧɨ ɧɚɩɪɚɜɥɟɧɢɸ ɫɤɨɪɨɫɬɢ ɨɬɧɨɫɢɬɟɥɶɧɨɝɨ ɞɜɢɠɟɧɢɹ ɬɟɥ ȣɨɬɧ : |
|
Fcɤ np ȣɨɬɧ . |
(2.14) |
ɋɢɥɨɜɨɟ ɩɨɥɟ – ɨɛɥɚɫɬɶ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɝɞɟ ɞɟɣɫɬɜɭɸɬ ɫɢɥɵ ɞɚɧɧɨɣ ɩɪɢɪɨɞɵ, ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ɡɚɜɢɫɹɳɢɟ ɤɚɤ ɨɬ ɜɪɟɦɟɧɢ, ɬɚɤ ɢ ɨɬ ɤɨɨɪɞɢɧɚɬɵ ɢ ɫɤɨɪɨɫɬɢ ɞɜɢɠɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ –
F(t, r, ȣ) .
2.2.Ɉɫɧɨɜɧɵɟ ɬɢɩɵ ɡɚɞɚɱ ɢ ɦɟɬɨɞɵ ɢɯ ɪɟɲɟɧɢɹ
2.2.1. Ʉɥɚɫɫɢɮɢɤɚɰɢɹ ɡɚɞɚɱ ɞɢɧɚɦɢɤɢ
ɉɪɹɦɚɹ ɡɚɞɚɱɚ ɞɢɧɚɦɢɤɢ – ɧɚɣɬɢ ɡɚɤɨɧ ɞɜɢɠɟɧɢɹ ɬɟɥɚ ɢɥɢ ɫɢɫɬɟɦɵ ɬɟɥ, ɟɫɥɢ ɢɡɜɟɫɬɧɵ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɷɬɢ ɬɟɥɚ.
Ɉɛɪɚɬɧɚɹ ɡɚɞɚɱɚ ɞɢɧɚɦɢɤɢ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ – ɧɚɣɬɢ ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɨ ɢɥɢ ɫɢɫɬɟɦɭ ɬɟɥ ɫɢɥɵ, ɟɫɥɢ ɢɡɜɟɫɬɧɵ ɡɚɤɨɧɵ ɞɜɢɠɟɧɢɹ ɷɬɢɯ ɬɟɥ.
Ȼɨɥɶɲɢɧɫɬɜɨ ɡɚɞɚɱ ɫɨɞɟɪɠɚɬ ɜ ɫɟɛɟ ɷɥɟɦɟɧɬɵ ɤɚɤ ɩɪɹɦɨɣ, ɬɚɤ ɢ ɨɛɪɚɬɧɨɣ ɡɚɞɚɱ ɞɢɧɚɦɢɤɢ. Ʉɚɤ ɩɪɚɜɢɥɨ, ɨɞɧɚ ɢɡ ɷɬɢɯ ɡɚɞɚɱ ɢɦɟɟɬ ɨɫɧɨɜɧɨɟ, ɞɪɭɝɚɹ – ɩɨɞɱɢɧɟɧɧɨɟ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɭɫɥɨɜɢɸ ɡɚɞɚɱɢ ɡɧɚɱɟɧɢɟ.
2.2.2.Ɉɛɳɚɹ ɫɯɟɦɚ ɪɟɲɟɧɢɹ ɡɚɞɚɱ ɞɢɧɚɦɢɤɢ
ɫɩɨɦɨɳɶɸ ɡɚɤɨɧɨɜ ɇɶɸɬɨɧɚ
I.Ɉɩɪɟɞɟɥɢɬɶɫɹ ɫ ɦɨɞɟɥɹɦɢ ɦɚɬɟɪɢɚɥɶɧɵɯ ɨɛɴɟɤɬɨɜ ɢ ɹɜɥɟɧɢɣ.
1.ɇɚɪɢɫɨɜɚɬɶ ɱɟɪɬɟɠ, ɧɚ ɤɨɬɨɪɨɦ ɢɡɨɛɪɚɡɢɬɶ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɟ ɬɟɥɚ.
2.ȼɵɛɪɚɬɶ ɫɢɫɬɟɦɭ ɨɬɫɱɟɬɚ ɢ ɢɡɨɛɪɚɡɢɬɶ ɧɚ ɱɟɪɬɟɠɟ ɟɟ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ (ɢɡ ɫɨɨɛɪɚɠɟɧɢɣ ɭɞɨɛɫɬɜɚ).
3.ɂɡɨɛɪɚɡɢɬɶ ɢ ɨɛɨɡɧɚɱɢɬɶ ɜɫɟ ɫɢɥɵ ɢ ɧɟɨɛɯɨɞɢɦɵɟ ɤɢɧɟɦɚɬɢɱɟɫɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɫɢɫɬɟɦɵ.
4.ȼɵɛɪɚɬɶ ɦɨɞɟɥɢ ɬɟɥ ɢ ɢɯ ɞɜɢɠɟɧɢɹ (ɟɫɥɢ ɷɬɨ ɧɟ ɫɞɟɥɚɧɨ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ).
II.Ɂɚɩɢɫɚɬɶ ɩɨɥɧɭɸ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ ɞɥɹ ɢɫɤɨɦɵɯ ɜɟɥɢɱɢɧ.
1.Ɂɚɩɢɫɚɬɶ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɨɫɢ ɤɨɨɪɞɢɧɚɬ ɞɥɹ ɜɫɟɯ ɬɟɥ ɫɢɫɬɟɦɵ.
52 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
2.ɂɫɩɨɥɶɡɨɜɚɬɶ ɬɪɟɬɢɣ ɡɚɤɨɧ ɇɶɸɬɨɧɚ, ɟɫɥɢ ɷɬɨ ɧɟ ɛɵɥɨ ɫɞɟɥɚɧɨ ɪɚɧɟɟ ɜ ɩ. 3.
3.ɂɫɩɨɥɶɡɨɜɚɬɶ ɡɚɤɨɧɵ, ɨɩɢɫɵɜɚɸɳɢɟ ɢɧɞɢɜɢɞɭɚɥɶɧɵɟ ɫɜɨɣɫɬɜɚ ɫɢɥ:
ɚ) ɡɚɤɨɧ ɜɫɟɦɢɪɧɨɝɨ ɬɹɝɨɬɟɧɢɹ, ɛ) ɡɚɤɨɧ Ƚɭɤɚ,
ɜ) ɡɚɤɨɧ Ⱥɦɨɧɬɨɧɚ – Ʉɭɥɨɧɚ ɢ ɬ.ɞ.
4.Ɂɚɩɢɫɚɬɶ ɭɪɚɜɧɟɧɢɹ ɤɢɧɟɦɚɬɢɱɟɫɤɢɯ ɫɜɹɡɟɣ.
5.ɂɫɩɨɥɶɡɨɜɚɬɶ ɪɟɡɭɥɶɬɚɬɵ ɪɚɧɟɟ ɪɟɲɟɧɧɵɯ ɡɚɞɚɱ ɢ ɨɫɨɛɵɟ ɭɫɥɨɜɢɹ ɡɚɞɚɱɢ.
III.ɉɨɥɭɱɢɬɶ ɢɫɤɨɦɵɣ ɪɟɡɭɥɶɬɚɬ ɜ ɚɧɚɥɢɬɢɱɟɫɤɨɦ ɢ ɱɢɫɥɟɧɧɨɦ ɜɢɞɚɯ.
1.Ɋɟɲɢɬɶ ɫɢɫɬɟɦɭ ɩɨɥɭɱɟɧɧɵɯ ɭɪɚɜɧɟɧɢɣ.
2.ɉɪɨɜɟɫɬɢ ɚɧɚɥɢɡ ɪɟɲɟɧɢɹ (ɩɪɨɜɟɪɢɬɶ ɪɚɡɦɟɪɧɨɫɬɶ ɢ ɥɢɲɧɢɟ ɤɨɪɧɢ, ɪɚɫɫɦɨɬɪɟɬɶ ɩɪɟɞɟɥɶɧɵɟ ɢ ɱɚɫɬɧɵɟ ɫɥɭɱɚɢ, ɭɫɬɚɧɨɜɢɬɶ ɨɛɥɚɫɬɶ ɩɪɢɦɟɧɢɦɨɫɬɢ).
3.ɉɨɥɭɱɢɬɶ ɱɢɫɥɟɧɧɵɣ ɪɟɡɭɥɶɬɚɬ.
ɉɪɢɦɟɱɚɧɢɹ.
ȼ ɫɥɭɱɚɟ ɪɟɲɟɧɢɹ ɡɚɞɚɱ ɧɚ ɞɢɧɚɦɢɤɭ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɩ. I.3 – II.1 ɪɟɱɶ ɢɞɟɬ ɨ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɯ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ, ɚ ɩ. II.2 ɧɚɞɨ ɨɩɭɫɬɢɬɶ.
ȼ ɫɥɭɱɚɟ ɪɟɲɟɧɢɹ ɡɚɞɚɱ ɧɚ ɞɢɧɚɦɢɤɭ ɩɪɨɫɬɟɣɲɢɯ ɦɟɯɚɧɢɱɟɫɤɢɯ ɫɢɫɬɟɦ ɜ ɩɩ. I.3 – II.2 ɪɟɱɶ ɢɞɟɬ ɨ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɯ ɢ ɭɪɚɜɧɟɧɢɹɯ ɞɜɢɠɟɧɢɹ ɬɟɥ ɢ ɫɢɥɚɯ, ɞɟɣɫɬɜɭɸɳɢɯ ɦɟɠɞɭ ɬɟɥɚɦɢ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɫɢɫɬɟɦɵ.
ɉɭɧɤɬɵ II.1 – II.4 (ɜ ɬɨɦ ɱɢɫɥɟ II.3.ɚ – II.3.ɜ) ɦɨɠɧɨ ɜɵɩɨɥɧɹɬɶ ɜ ɬɨɣ ɢɥɢ ɢɧɨɣ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɢ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɪɟɲɚɟɦɨɣ ɡɚɞɚɱɢ.
2.3. ɉɪɢɦɟɪɵ ɪɟɲɟɧɢɹ ɡɚɞɚɱ
Ɂɚɞɚɱɚ 2.1
(Ɇɚɲɢɧɚ Ⱥɬɜɭɞɚ)
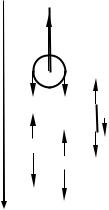
ɑɟɪɟɡ ɛɥɨɤ, ɩɨɞɜɟɲɟɧɧɵɣ ɤ ɩɨɬɨɥɤɭ ɩɟɪɟɤɢɧɭɬɚ ɧɢɬɶ. Ʉ ɤɨɧɰɚɦ ɧɢɬɢ ɩɪɢɤɪɟɩɥɟɧɵ ɞɜɚ ɝɪɭɡɚ ɦɚɫɫɚɦɢ m1 ɢ m2. Ɉɩɪɟɞɟɥɢɬɶ ɭɫɤɨɪɟɧɢɹ ɬɟɥ.
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
53 |
Ɋɟɲɟɧɢɟ
Ɋɟɲɟɧɢɟ ɞɚɧɧɨɣ ɡɚɞɚɱɢ (ɢ ɜɫɟɯ ɩɨɫɥɟɞɭɸɳɢɯ) ɛɭɞɟɦ ɩɪɨɜɨɞɢɬɶ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɩɪɟɞɥɨɠɟɧɧɨɣ ɫɯɟɦɨɣ ɪɟɲɟɧɢɹ ɡɚɞɚɱ ɞɢɧɚɦɢɤɢ.
I. ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.4, ɢ ɢɡɨɛɪɚɡɢɦ ɧɚ ɧɟɦ ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɚ ɫɢɫɬɟɦɵ ɫɢɥɵ: ɫɢɥɵ ɬɹɠɟɫɬɢ ɢ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɫɨ ɫɬɨɪɨɧɵ ɧɢɬɟɣ.
ȼɵɛɟɪɟɦ ɦɨɞɟɥɢ ɬɟɥ ɢ ɢɯ ɞɜɢɠɟɧɢɣ. Ƚɪɭɡɵ ɫɱɢɬɚɟɦ ɦɚɬɟɪɢɚɥɶɧɵɦɢ ɬɨɱɤɚɦɢ, ɩɨɞɜɟɲɟɧɧɵɦɢ ɧɚ ɧɟɜɟɫɨɦɨɣ ɢ ɧɟɪɚɫɬɹɠɢɦɨɣ ɧɢɬɢ, ɩɟɪɟɤɢɧɭɬɨɣ ɱɟɪɟɡ ɧɟɜɟɫɨɦɵɣ ɚɛɫɨɥɸɬɧɨ ɬɜɟɪɞɵɣ ɰɢɥɢɧɞɪɢɱɟɫɤɢɣ ɛɥɨɤ. Ȼɭɞɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɝɪɭɡɵ ɞɜɢɠɭɬɫɹ ɜɟɪɬɢɤɚɥɶɧɨ, ɧɢɬɶ ɧɟ ɩɪɨɫɤɚɥɶɡɵɜɚɟɬ ɨɬɧɨɫɢɬɟɥɶɧɨ ɛɥɨɤɚ, ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜɨɡɞɭɯɚ ɢ ɬɪɟɧɢɹ ɜ ɨɫɢ ɛɥɨɤɚ ɧɟɬ.
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ |
|
|
|
|
|
|
|
|
|
|
|
|
||
ɞɜɭɯ ɝɪɭɡɨɜ ɜ ɩɪɨɟɤɰɢɢ ɧɚ ɨɫɶ X (ɫɦ. |
|
|
|
|
|
T |
||||||||
ɪɢɫ. 2.4) ɢ ɭɪɚɜɧɟɧɢɟ ɤɢɧɟɦɚɬɢɱɟɫɤɨɣ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
ɫɜɹɡɢ, ɹɜɥɹɸɳɟɟɫɹ ɫɥɟɞɫɬɜɢɟɦ ɧɟɪɚɫ- |
|
|
|
|
|
|
|
|
|
|
|
|||
ɬɹɠɢɦɨɫɬɢ ɧɢɬɢ: |
|
|
|
|
|
|
|
|
|
|
|
Tɜ |
||
|
|
|
|
|
|
|
|
|
|
|
||||
m1a1 |
m1g T1, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
T1 |
|
|
T2 |
|
|
|
|
|
||||
m2a2 |
m2 g T2 , |
(2.15) |
|
|
|
|
|
|
|
|
||||
|
T1 |
|
|
|
|
|
|
|
|
mɧg |
||||
a1 a2 |
0. |
|
|
|
|
T2 |
|
|
|
|
||||
Ɂɞɟɫɶ a1 ɢ |
a2 – ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɣ |
|
|
|
|
|
|
|
Tɧ |
|||||
|
|
|
|
|
|
|
|
|
||||||
ɝɪɭɡɨɜ ɧɚ ɨɫɶ X, T1 ɢ T2 |
– ɦɨɞɭɥɢ ɫɢɥ, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɝɪɭɡɵ ɫɨ ɫɬɨɪɨɧɵ ɧɢ- |
m1g |
m2g |
||||||||||||
ɬɢ. |
|
X |
|
|
|
|
||||||||
Ⱦɨɤɚɠɟɦ ɩɨɫɬɨɹɧɫɬɜɨ ɦɨɞɭɥɹ ɫɢ- |
Ɋɢɫ. 2.4 |
|
ɥɵ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ ɜɞɨɥɶ ɜɫɟɣ ɟɟ ɞɥɢ- |
||
|
ɧɵ ɜ ɭɫɥɨɜɢɹɯ ɞɚɧɧɨɣ ɡɚɞɚɱɢ. Ⱦɥɹ ɷɬɨɝɨ ɜɵɞɟɥɢɦ ɦɵɫɥɟɧɧɨ ɩɪɹɦɨɥɢɧɟɣɧɵɣ ɭɱɚɫɬɨɤ ɧɢɬɢ ɩɪɨɢɡɜɨɥɶɧɨɣ ɞɥɢɧɵ (ɫɦ. ɪɢɫ. 2.4) ɢ ɡɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɟ ɟɝɨ ɞɜɢɠɟɧɢɹ ɜ ɩɪɨɟɤɰɢɢ ɧɚ ɨɫɶ X:
mɧ aɧ Tɧ Tɜ mɧ g Fɫɨɩɪ , |
(2.16) |
ɝɞɟ mɧ – ɦɚɫɫɚ ɜɵɞɟɥɟɧɧɨɝɨ ɭɱɚɫɬɤɚ ɧɢɬɢ, aɧ |
– ɩɪɨɟɤɰɢɹ ɟɝɨ ɭɫɤɨ- |
ɪɟɧɢɹ ɧɚ ɨɫɶ X, Tɧ ɢ Tɜ – ɦɨɞɭɥɢ ɫɢɥ ɧɚɬɹɠɟɧɢɹ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɜɵɞɟɥɟɧɧɵɣ ɭɱɚɫɬɨɤ ɧɢɬɢ ɫɨ ɫɬɨɪɨɧɵ ɧɢɠɧɟɝɨ ɢ ɜɟɪɯɧɟɝɨ ɩɪɢɦɵɤɚɸɳɢɯ ɤ ɧɟɦɭ ɭɱɚɫɬɤɨɜ ɧɢɬɢ, Fɫɨɩɪ – ɩɪɨɟɤɰɢɹ ɫɢɥɵ ɫɨɩɪɨɬɢɜɥɟ-
ɧɢɹ ɜɨɡɞɭɯɚ.
54 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
ɉɨɫɤɨɥɶɤɭ ɧɢɬɶ ɩɨ ɭɫɥɨɜɢɸ ɡɚɞɚɱɢ ɧɟɜɟɫɨɦɚ ɢ ɧɟɬ ɫɢɥɵ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜɨɡɞɭɯɚ, ɬɨ ɢɡ (2.16) ɫɥɟɞɭɟɬ, ɱɬɨ ɦɨɞɭɥɶ ɫɢɥɵ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ ɩɨɫɬɨɹɧɟɧ ɜɞɨɥɶ ɩɪɹɦɨɥɢɧɟɣɧɨɝɨ ɭɱɚɫɬɤɚ ɧɢɬɢ, ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɫɢɥɚ, ɩɪɢɥɨɠɟɧɧɚɹ ɤ ɝɪɭɡɭ ɫɨ ɫɬɨɪɨɧɵ ɧɢɬɢ ɢ ɫɢɥɚ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ ɜ ɜɟɪɯɧɟɣ ɱɚɫɬɢ ɩɪɹɦɨɥɢɧɟɣɧɨɝɨ ɭɱɚɫɬɤɚ ɪɚɜɧɵ ɩɨ ɦɨɞɭɥɸ.
Ⱦɥɹ ɞɨɤɚɡɚɬɟɥɶɫɬɜɚ ɪɚɜɟɧɫɬɜɚ ɦɨɞɭɥɟɣ ɫɢɥ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ ɨɬ ɛɥɨɤɚ ɡɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɟ ɜɪɚɳɚɬɟɥɶɧɨɝɨ ɞɜɢɠɟɧɢɹ (ɫɦ. (6.30) ɜ Ƚɥɚɜɟ 6) ɛɥɨɤɚ ɜɦɟɫɬɟ ɫ ɩɪɢɦɵɤɚɸɳɢɦ ɤ ɧɟɦɭ ɭɱɚɫɬɤɨɦ ɧɢɬɢ (ɫɦ. ɪɢɫ. 2.4):
J |
dZ |
T R T R M |
ɬɪ |
M |
ɫɨɩɪ |
, |
(2.17) |
|
|||||||
|
dt |
1 2 |
|
|
|
||
|
|
|
|
|
|
|
ɝɞɟ J – ɦɨɦɟɧɬ ɢɧɟɪɰɢɢ ɛɥɨɤɚ ɜɦɟɫɬɟ ɫ ɩɪɢɦɵɤɚɸɳɢɦ ɤ ɧɟɦɭ ɭɱɚɫɬɤɨɦ ɧɢɬɢ ɨɬɧɨɫɢɬɟɥɶɧɨ ɨɫɢ, ɩɪɨɯɨɞɹɳɟɣ ɱɟɪɟɡ ɰɟɧɬɪ ɛɥɨɤɚ ɢ ɧɚɩɪɚɜɥɟɧɧɨɣ ɡɚ ɩɥɨɫɤɨɫɬɶ ɱɟɪɬɟɠɚ, Z – ɭɝɥɨɜɚɹ ɫɤɨɪɨɫɬɶ ɜɪɚɳɟɧɢɹ ɛɥɨɤɚ, M ɬɪ – ɦɨɦɟɧɬ ɫɢɥ ɬɪɟɧɢɹ, ɞɟɣɫɬɜɭɸɳɢɯ ɜ ɨɫɢ ɛɥɨɤɚ,
M ɫɨɩɪ – ɦɨɦɟɧɬ ɫɢɥ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜɨɡɞɭɯɚ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɛɥɨɤ.
ɉɨɫɤɨɥɶɤɭ ɛɥɨɤ ɢ ɧɢɬɶ ɧɟɜɟɫɨɦɵ, ɧɟɬ ɬɪɟɧɢɹ ɜ ɨɫɢ ɛɥɨɤɚ ɢ ɫɢɥɵ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜɨɡɞɭɯɚ, ɬɨ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (2.17) ɦɨɞɭɥɢ ɫɢɥ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ ɫɥɟɜɚ ɢ ɫɩɪɚɜɚ ɨɬ ɛɥɨɤɚ ɪɚɜɧɵ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɪɚɜɧɵ ɢ ɫɢɥɵ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ, ɩɪɢɥɨɠɟɧɧɵɟ ɤ ɝɪɭɡɚɦ:
T1 |
T2 . |
|
|
|
|
|
|
|
(2.18) |
|
III. Ɋɟɲɢɦ ɩɨɥɭɱɟɧɧɭɸ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ (2.15) ɢ (2.17) ɨɬ- |
||||||||||
ɧɨɫɢɬɟɥɶɧɨ ɢɫɤɨɦɵɯ ɮɢɡɢɱɟɫɤɢɯ ɜɟɥɢɱɢɧ: |
|
|||||||||
a |
g |
m1 |
m2 |
, a |
2 |
g |
m1 |
m2 |
. |
(2.19) |
|
|
|
|
|||||||
1 |
|
m1 |
m2 |
|
m1 |
m2 |
|
|||
|
|
|
|
|
||||||
Ⱦɥɹ ɨɰɟɧɤɢ ɩɪɚɜɢɥɶɧɨɫɬɢ ɩɨɥɭɱɟɧɧɨɝɨ ɪɟɡɭɥɶɬɚɬɚ ɩɪɨɚɧɚɥɢɡɢɪɭɟɦ ɱɚɫɬɧɵɟ ɢ ɩɪɟɞɟɥɶɧɵɟ ɫɥɭɱɚɢ. ȿɫɥɢ ɤ ɧɢɬɢ ɩɨɞɜɟɲɟɧɵ ɝɪɭɡɵ ɨɞɢɧɚɤɨɜɨɣ ɦɚɫɫɵ, ɬɨ ɩɨɥɭɱɟɧɧɵɟ ɮɨɪɦɭɥɵ ɞɥɹ ɩɪɨɟɤɰɢɣ ɭɫɤɨɪɟɧɢɣ ɞɚɸɬ ɡɧɚɱɟɧɢɟ, ɪɚɜɧɨɟ ɧɭɥɸ, ɱɬɨ ɨɱɟɜɢɞɧɨ ɢ ɢɡ ɨɛɳɢɯ ɫɨɨɛɪɚɠɟɧɢɣ. ȿɫɥɢ m1 >> m2, ɬɨ a1 = g, a2 = íg. ɉɪɢ ɜɵɩɨɥɧɟɧɢɢ ɨɛɪɚɬɧɨɝɨ ɧɟɪɚɜɟɧɫɬɜɚ m1 << m2, ɭɫɤɨɪɟɧɢɹ ɝɪɭɡɨɜ ɪɚɜɧɵ a1 = íg ɢ a2 = g. ɗɬɢ ɩɪɟɞɟɥɶɧɵɟ ɡɧɚɱɟɧɢɹ ɥɟɝɤɨ ɩɨɥɭɱɢɬɶ ɢɡ ɮɢɡɢɱɟɫɤɢɯ ɫɨɨɛɪɚɠɟɧɢɣ. ȿɫɥɢ ɨɞɢɧ ɢɡ ɝɪɭɡɨɜ ɢɦɟɟɬ ɫɭɳɟɫɬɜɟɧɧɨ ɛóɥɶɲɭɸ ɦɚɫɫɭ, ɱɟɦ ɜɬɨɪɨɣ, ɬɨ ɨɧ ɩɚɞɚɟɬ ɫ ɭɫɤɨɪɟɧɢɟɦ ɫɜɨɛɨɞɧɨɝɨ ɩɚɞɟɧɢɹ. ɍɫɤɨɪɟɧɢɟ ɜɬɨɪɨɝɨ ɝɪɭɡɚ ɜ ɫɢɥɭ ɧɟɪɚɫɬɹɠɢɦɨɫɬɢ ɧɢɬɢ ɪɚɜɧɨ ɩɨ ɜɟɥɢɱɢɧɟ ɭɫɤɨɪɟɧɢɸ ɩɟɪɜɨɝɨ ɝɪɭɡɚ ɢ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨ ɩɨ ɧɚɩɪɚɜɥɟɧɢɸ.
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
55 |
||||||
|
|
|
|
Ɂɚɞɚɱɚ 2.2 |
|
|
|
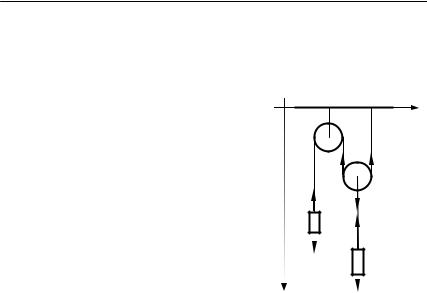
ɇɚɣɬɢ ɭɫɤɨɪɟɧɢɹ ɬɟɥ ɢ ɫɢɥɵ ɧɚɬɹɠɟɧɢɹ ɧɢɬɟɣ ɞɥɹ ɫɢɫɬɟɦɵ |
|||||||
ɬɟɥ, ɢɡɨɛɪɚɠɟɧɧɨɣ ɧɚ ɪɢɫɭɧɤɟ. |
|
|
|||||
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
I. ȼɵɛɟɪɟɦ |
ɫɢɫɬɟɦɭ |
ɤɨɨɪɞɢɧɚɬ |
|
|
|||
ɬɚɤ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.5, ɢ ɢɡɨɛɪɚ- |
|
Y |
|||||
ɡɢɦ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɚ ɫɢɫ- |
|
||||||
|
|
||||||
ɬɟɦɵ. |
|
|
|
|
|
|
|
ȼɵɛɟɪɟɦ ɦɨɞɟɥɶ, ɚɧɚɥɨɝɢɱɧɭɸ |
T1 |
T1 |
|||||
ɬɨɣ, ɤɨɬɨɪɚɹ ɛɵɥɚ ɢɫɩɨɥɶɡɨɜɚɧɚ ɜ ɩɪɟ- |
T1 |
|
|||||
ɞɵɞɭɳɟɣ ɡɚɞɚɱɟ: ɝɪɭɡɵ ɫɱɢɬɚɟɦ ɦɚɬɟ- |
T2 |
||||||
ɪɢɚɥɶɧɵɦɢ |
ɬɨɱɤɚɦɢ, ɩɨɞɜɟɲɟɧɧɵɦɢ |
T2 |
|
||||
ɧɚ ɧɟɜɟɫɨɦɵɯ ɢ ɧɟɪɚɫɬɹɠɢɦɵɯ ɧɢɬɹɯ, |
|
||||||
|
|
||||||
ɩɟɪɟɤɢɧɭɬɵɯ ɱɟɪɟɡ ɧɟɜɟɫɨɦɵɟ ɚɛɫɨ- |
m1g |
|
|||||
ɥɸɬɧɨ ɬɜɟɪɞɵɟ ɰɢɥɢɧɞɪɢɱɟɫɤɢɟ ɛɥɨ- |
|
||||||
ɤɢ. Ȼɭɞɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɝɪɭɡɵ ɞɜɢɠɭɬɫɹ |
X |
m2g |
|||||
ɜɟɪɬɢɤɚɥɶɧɨ, ɧɢɬɶ ɧɟ ɩɪɨɫɤɚɥɶɡɵɜɚɟɬ |
|||||||
|
|
||||||
ɨɬɧɨɫɢɬɟɥɶɧɨ |
ɛɥɨɤɨɜ, ɫɨɩɪɨɬɢɜɥɟɧɢɹ |
Ɋɢɫ. 2.5 |
|||||
ɜɨɡɞɭɯɚ ɢ ɬɪɟɧɢɹ ɜ ɨɫɢ ɛɥɨɤɨɜ ɧɟɬ. |
|
|
|||||
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɝɪɭɡɨɜ ɜ ɩɪɨɟɤɰɢɢ ɧɚ ɨɫɶ X |
|||||||
ɜɵɛɪɚɧɧɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ: |
|
|
|||||
m1a1 |
m1g T1 , |
|
|
(2.20) |
|||
m2a2 |
m2 g T2 . |
|
|
(2.21) |
|||
Ɂɞɟɫɶ a1 ɢ a2 |
– ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɣ ɝɪɭɡɨɜ ɧɚ ɨɫɶ X, T1 |
ɢ T2 – ɦɨ- |
|||||
ɞɭɥɢ ɫɢɥ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɝɪɭɡɵ ɫɨ ɫɬɨɪɨɧɵ ɧɢɬɟɣ. |
|
||||||
Ɉɛɨɡɧɚɱɢɦ ɤɨɨɪɞɢɧɚɬɵ ɬɟɥ ɢ ɩɨɞɜɢɠɧɨɝɨ ɛɥɨɤɚ x1, x2 ɢ xɛɥ |
|||||||
ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ. Ɂɚɩɢɲɟɦ ɭɫɥɨɜɢɹ ɧɟɪɚɫɬɹɠɢɦɨɫɬɢ ɧɢɬɟɣ (ɫɦ. |
|||||||
ɪɢɫ. 2.5) ɜ ɜɢɞɟ: |
|
|
|
|
|||
x1 2xɛɥ |
const , |
|
|
(2.22) |
|||
x2 xɛɥ |
const . |
|
|
(2.23) |
|||
Ⱦɜɚɠɞɵ ɞɢɮɮɟɪɟɧɰɢɪɭɹ (2.22) ɢ (2.23) ɩɨ ɜɪɟɦɟɧɢ, ɩɨɥɭɱɢɦ |
|||||||
ɭɪɚɜɧɟɧɢɟ ɤɢɧɟɦɚɬɢɱɟɫɤɨɣ ɫɜɹɡɢ ɞɥɹ ɭɫɤɨɪɟɧɢɣ ɝɪɭɡɨɜ: |
|
||||||
a1 2a2 |
0 . |
|
|
|
(2.24) |
||
ȼ ɪɚɦɤɚɯ ɩɪɢɧɹɬɨɣ ɦɨɞɟɥɢ ɫɢɥɵ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ ɫ ɨɛɟɢɯ ɫɬɨ- |
|||||||
ɪɨɧ ɥɸɛɨɝɨ ɢɡ ɛɥɨɤɨɜ ɪɚɜɧɵ (ɫɦ. ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ 1). ɋɜɹɡɶ ɦɟɠɞɭ |
|||||||
ɫɢɥɚɦɢ ɧɚɬɹɠɟɧɢɹ ɪɚɡɧɵɯ ɧɢɬɟɣ ɧɚɣɞɟɦ ɢɡ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ |
|||||||
ɩɨɞɜɢɠɧɨɝɨ ɛɥɨɤɚ: |
|
|
|
||||
56 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
mɛɥ aɛɥ T2 2T1 , |
(2.25) |
ɝɞɟ ɦɚɫɫɚ ɩɨɞɜɢɠɧɨɝɨ ɛɥɨɤɚ mɛɥ 0 .
III.Ɋɟɲɚɹ ɩɨɥɭɱɟɧɧɭɸ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ (2.20), (2.21), (2.24)
ɢ(2.25), ɩɨɥɭɱɚɟɦ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɢɫɤɨɦɵɯ ɜɟɥɢɱɢɧ:
a |
2g |
2m1 m2 |
, |
|
|
|
|
(2.26) |
|||||
|
|
|
|
|
|
||||||||
1 |
|
|
4m1 m2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
a2 |
g |
m2 2m1 |
, |
|
|
|
|
(2.27) |
|||||
|
|
|
|
||||||||||
|
|
4m1 m2 |
|
|
|
|
|||||||
T1 |
m1 g a1 |
|
|
|
3m1m2 g |
, |
|
(2.28) |
|||||
|
|
4m1 m2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
T2 |
2m1 |
g a1 |
|
|
|
|
6m1m2 g |
. |
(2.29) |
||||
|
|
4m1 m2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Ɋɚɫɫɦɨɬɪɢɦ ɱɚɫɬɧɵɟ ɢ ɩɪɟɞɟɥɶɧɵɟ ɫɥɭɱɚɢ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ |
|||||||||||||
(2.26) – (2.29). |
|
|
|
|
|
|
|
|
|
||||
1. ȿɫɥɢ |
2m1 |
m2 , |
ɬɨ ɝɪɭɡɵ ɩɨɤɨɹɬɫɹ ɢɥɢ ɞɜɢɝɚɸɬɫɹ ɪɚɜɧɨ- |
||||||||||
ɦɟɪɧɨ ɢ ɩɪɹɦɨɥɢɧɟɣɧɨ: |
|
|
|
|
|||||||||
a1 |
a2 |
0 . |
|
|
|
|
|
|
|
|
|
||
ɉɪɢ ɷɬɨɦ ɫɢɥɵ ɧɚɬɹɠɟɧɢɹ ɧɢɬɟɣ ɪɚɜɧɵ: |
|
||||||||||||
T2 |
2T1 |
2m1g . |
|
|
|
|
|||||||
2. ȿɫɥɢ |
m2 !! m1 , ɬɨ ɬɟɥɨ ɦɚɫɫɨɣ m2 |
ɛɭɞɟɬ ɩɚɞɚɬɶ ɫ ɭɫɤɨɪɟ- |
|||||||||||
ɧɢɟɦ ɫɜɨɛɨɞɧɨɝɨ ɩɚɞɟɧɢɹ: |
|
|
|
||||||||||
a2 |
g , |
|
|
|
|
|
|
|
|
|
|
||
ɚ ɬɟɥɨ ɦɚɫɫɨɣ m1 ɩɨɞɧɢɦɚɬɶɫɹ ɜɜɟɪɯ ɫ ɭɞɜɨɟɧɧɵɦ ɩɨ ɦɨɞɭɥɸ ɭɫɤɨɪɟɧɢɟɦ:
a1 2g .
ɉɪɢ ɷɬɨɦ:
T2 2T1 6m1g .
3. ȿɫɥɢ m1 !! m2 , ɬɨ ɬɟɥɨ ɦɚɫɫɨɣ m1 ɛɭɞɟɬ ɩɚɞɚɬɶ ɫ ɭɫɤɨɪɟɧɢɟɦ ɫɜɨɛɨɞɧɨɝɨ ɩɚɞɟɧɢɹ:
a1 g ,
ɚ ɬɟɥɨ ɦɚɫɫɨɣ m2 ɩɨɞɧɢɦɚɬɶɫɹ ɜɜɟɪɯ ɫ ɭɫɤɨɪɟɧɢɟɦ
a2 0,5g .
ɉɪɢ ɷɬɨɦ:
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
57 |
T |
2T |
3 |
m g . |
|
|||
2 |
1 |
2 |
1 |
|
|
|
Ɂɚɞɚɱɚ 2.3
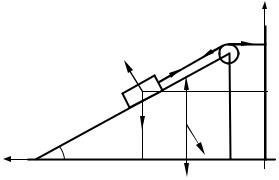
ȼ ɫɢɫɬɟɦɟ ɬɟɥ, ɢɡɨɛɪɚɠɟɧɧɵɯ ɧɚ ɪɢɫ. 2.6, ɢɡɜɟɫɬɧɵ ɦɚɫɫɵ ɛɪɭɫɤɚ m ɢ ɤɥɢɧɚ M, ɚ ɬɚɤɠɟ ɭɝɨɥ D ɩɪɢ ɨɫɧɨɜɚɧɢɢ ɤɥɢɧɚ. Ɇɚɫɫɵ ɛɥɨɤɚ ɢ ɧɢɬɢ ɩɪɟɧɟɛɪɟɠɢɦɨ ɦɚɥɵ, ɧɢɬɶ ɧɟɪɚɫɬɹɠɢɦɚ, ɬɪɟɧɢɹ ɧɟɬ. ɇɚɣɬɢ ɭɫɤɨɪɟɧɢɟ ɤɥɢɧɚ A .
|
|
|
|
|
Y |
|
|
T |
|
T |
y0 |
|
N |
|
|
||
|
|
|
|
||
|
T |
|
|
|
|
|
|
R |
|
|
y |
|
|
|
|
|
|
|
mg |
|
N |
|
|
|
D |
|
|
|
|
X |
x |
Mg |
xɤ |
|
0 |
|
|
|
|
|
|
|
Ɋɢɫ. 2.6 |
|
|
|
|
|
Ɋɟɲɟɧɢɟ |
|
|
|
|
I. ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.6. ɂɡɨɛɪɚɡɢɦ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɚ ɫɢɫɬɟɦɵ: mg ɢ Mg – ɫɢɥɵ ɬɹɠɟɫɬɢ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɛɪɭɫɨɤ ɢ ɤɥɢɧ, ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ; R – ɫɢɥɚ ɪɟɚɤɰɢɢ ɨɩɨɪɵ, ɞɟɣɫɬɜɭɸɳɚɹ ɧɚ ɤɥɢɧ; N – ɫɢɥɚ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɛɪɭɫɤɚ ɢ ɤɥɢɧɚ. ɉɪɢ ɷɬɨɦ ɭɱɬɟɦ, ɱɬɨ ɫɢɥɚ ɧɚɬɹɠɟɧɢɹ ɧɢɬɢ T ɩɨɫɬɨɹɧɧɚ ɜɞɨɥɶ ɜɫɟɣ ɟɟ ɞɥɢɧɵ ɜ ɪɚɦɤɚɯ ɩɪɢɧɹɬɵɯ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ ɦɨɞɟɥɟɣ ɬɟɥ ɫɢɫɬɟɦɵ, ɚ ɫɢɥɵ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɛɪɭɫɤɚ ɢ ɤɥɢɧɚ ɪɚɜɧɵ ɩɨ ɜɟɥɢɱɢɧɟ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɬɪɟɬɶɢɦ ɡɚɤɨɧɨɦ ɇɶɸɬɨɧɚ ɢ ɧɚɩɪɚɜɥɟɧɵ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɩɨɜɟɪɯɧɨɫɬɢ ɢɯ ɫɨɩɪɢɤɨɫɧɨɜɟɧɢɹ ɢɡ-ɡɚ ɨɬɫɭɬɫɬɜɢɹ ɫɢɥ ɬɪɟɧɢɹ.
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ ɢ ɤɥɢɧɚ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɨɫɢ ɜɵɛɪɚɧɧɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ ɢ ɭɱɬɟɦ ɩɪɢ ɷɬɨɦ, ɱɬɨ ɤɥɢɧ
ɦɨɠɟɬ ɞɜɢɝɚɬɶɫɹ ɬɨɥɶɤɨ ɜɞɨɥɶ ɨɫɢ X ( Ay |
0 ): |
max N sin D T cosD , |
(2.30) |
58 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
|
may |
N cosD mg T sin D , |
(2.31) |
MAx |
N sin D T cosD T , |
(2.32) |
0 R N cosD Mg T sin D . |
(2.33) |
|
Ⱦɨɩɨɥɧɢɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ (2.30) – (2.33) ɭɪɚɜɧɟɧɢɟɦ ɤɢɧɟɦɚɬɢɱɟɫɤɨɣ ɫɜɹɡɢ, ɤɨɬɨɪɨɟ ɫɥɟɞɭɟɬ ɢɡ ɭɫɥɨɜɢɹ ɧɟɪɚɫɬɹɠɢɦɨɫɬɢ ɧɢɬɢ:
xɤ |
|
x xɤ |
|
const , |
|
|
cosD |
||||
|
|
|
|||
xɤ |
y0 y |
const . |
|||
sin D |
|||||
|
|
|
|||
Ⱦɢɮɮɟɪɟɧɰɢɪɭɹ (2.34) |
– (2.35) ɞɜɚɠɞɵ ɩɨ ɜɪɟɦɟɧɢ, ɩɨɥɭɱɢɦ: |
|||||
A |
ax Ax |
0 , |
|
|||
|
|
|
||||
x |
|
|
cosD |
|
|
|
|
|
|
|
|
||
Ax |
|
|
ay |
|
0 . |
|
|
sin D |
|
||||
|
|
|
|
|
||
(2.34)
(2.35)
(2.36)
(2.37)
III. ɉɪɟɨɛɪɚɡɭɟɦ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ (2.30) – (2.32), (2.36), (2.37), ɢɫɤɥɸɱɢɜ ɢɡ ɧɢɯ ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɹ ɛɪɭɫɤɚ ax ɢ ay . ɍɪɚɜ-
ɧɟɧɢɟ (2.33) ɧɟ ɬɪɟɛɭɟɬɫɹ ɞɥɹ ɪɟɲɟɧɢɹ ɩɨɫɬɚɜɥɟɧɧɨɣ ɡɚɞɚɱɢ (ɧɟ ɬɪɟɛɭɟɬɫɹ ɧɚɯɨɠɞɟɧɢɹ ɫɢɥɵ ɪɟɚɤɰɢɢ ɨɩɨɪɵ, ɞɟɣɫɬɜɭɸɳɟɣ ɧɚ ɤɥɢɧ R). ȼ ɪɟɡɭɥɶɬɚɬɟ ɩɨɥɭɱɢɦ ɫɥɟɞɭɸɳɭɸ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ:
mAx 1 cosD |
N sinD T cosD , |
(2.38) |
|||||
mAx sin D N cosD mg T sin D , |
(2.39) |
||||||
MAx |
N sin D T cosD T . |
(2.40) |
|||||
Ɋɟɲɢɜ ɷɬɭ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɣ, ɨɩɪɟɞɟɥɢɦ ɩɪɨɟɤɰɢɸ ɭɫɤɨɪɟ- |
|||||||
ɧɢɹ ɤɥɢɧɚ ɧɚ ɨɫɶ X: |
sin D |
|
|
|
|||
Ax |
g |
|
. |
(2.41) |
|||
M / m |
2 1 cosD |
||||||
|
|
|
|
||||
ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɩɨɥɭɱɟɧɧɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɹ ɤɥɢɧɚ Ax . ȿɫɥɢ ɦɚɫɫɚ ɤɥɢɧɚ ɡɧɚɱɢɬɟɥɶɧɨ ɛɨɥɶɲɟ ɦɚɫɫɵ ɛɪɭ-
ɫɤɚ (M >> m), ɬɨ ɭɫɤɨɪɟɧɢɟ ɤɥɢɧɚ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɨɥɶ. ɇɟɩɨɞɜɢɠɧɵɦ ɩɪɢ ɷɬɨɦ ɨɫɬɚɟɬɫɹ ɢ ɛɪɭɫɨɤ. ȿɫɥɢ ɭɝɨɥ ɩɪɢ ɨɫɧɨɜɚɧɢɢ ɤɥɢɧɚ ɪɚɜɟɧ ɧɭɥɸ, ɬɨ ɧɟɬ ɫɢɥ, ɤɨɬɨɪɵɟ ɦɨɝɥɢ ɛɵ ɜɵɡɜɚɬɶ ɞɜɢɠɟɧɢɟ ɤɥɢɧɚ
– ɭɫɤɨɪɟɧɢɟ ɤɥɢɧɚ ɬɚɤɠɟ ɪɚɜɧɨ ɧɭɥɸ.
Ƚɥɚɜɚ 2. Ⱦɢɧɚɦɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ |
59 |
Ɂɚɞɚɱɚ 2.4
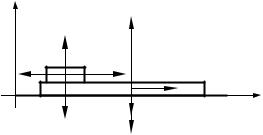
ɇɚ ɞɨɫɤɟ ɦɚɫɫɨɣ Ɇ ɥɟɠɢɬ ɛɪɭɫɨɤ ɦɚɫɫɨɣ m. Ʉɨɷɮɮɢɰɢɟɧɬ ɬɪɟɧɢɹ ɦɟɠɞɭ ɞɨɫɤɨɣ ɢ ɛɪɭɫɤɨɦ ɪɚɜɟɧ P. Ⱦɨɫɤɚ ɦɨɠɟɬ ɞɜɢɝɚɬɶɫɹ ɩɨ ɝɥɚɞɤɨɣ ɝɨɪɢɡɨɧɬɚɥɶɧɨɣ ɩɨɜɟɪɯɧɨɫɬɢ. Ʉ ɛɪɭɫɤɭ ɩɪɢɤɥɚɞɵɜɚɟɬɫɹ ɝɨɪɢɡɨɧɬɚɥɶɧɚɹ ɫɢɥɚ F, ɦɨɞɭɥɶ ɤɨɬɨɪɨɣ ɡɚɜɢɫɢɬ ɨɬ ɜɪɟɦɟɧɢ ɩɨ ɡɚɤɨɧɭ F = Dt, ɝɞɟ D = const. Ɉɩɪɟɞɟɥɢɬɶ ɫɤɨɪɨɫɬɢ ɛɪɭɫɤɚ X(t) ɢ ɞɨɫɤɢ V(t) ɫɩɭɫɬɹ ɜɪɟɦɹ t ɩɨɫɥɟ ɧɚɱɚɥɚ ɞɟɣɫɬɜɢɹ ɫɢɥɵ.
Ɋɟɲɟɧɢɟ
I. ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɯɚɪɚɤɬɟɪ ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ. ɉɪɢ ɦɚɥɨɣ ɜɟɥɢɱɢɧɟ ɩɪɢɥɨɠɟɧɧɨɣ ɤ ɛɪɭɫɤɭ ɝɨɪɢɡɨɧɬɚɥɶɧɨɣ ɫɢɥɵ F ɞɨɫɤɚ ɢ ɛɪɭɫɨɤ ɛɭɞɭɬ ɞɜɢɝɚɬɶɫɹ ɫ ɨɞɢɧɚɤɨɜɵɦ ɭɫɤɨɪɟɧɢɟɦ, ɩɨɫɤɨɥɶɤɭ ɫɢɥɚ ɬɪɟɧɢɹ ɩɨɤɨɹ ɧɟ ɞɨɫɬɢɝɧɟɬ ɟɳɟ ɦɚɤɫɢɦɚɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ. ȼ ɧɟɤɨɬɨɪɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ t0 ɫɢɥɚ ɬɪɟɧɢɹ ɩɨɤɨɹ ɞɨɫɬɢɝɧɟɬ
ɦɚɤɫɢɦɚɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ, ɪɚɜɧɨɝɨ ɫɢɥɟ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ, ɢ ɜ ɞɚɥɶɧɟɣɲɟɦ ɛɭɞɟɬ ɩɪɨɢɫɯɨɞɢɬɶ ɫɤɨɥɶɠɟɧɢɟ ɛɪɭɫɤɚ ɩɨ ɞɨɫɤɟ, ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɭɫɤɨɪɟɧɢɹ ɬɟɥ ɫɢɫɬɟɦɵ ɛɭɞɭɬ ɢɡɦɟɧɹɬɶɫɹ ɩɨ ɪɚɡɥɢɱɧɵɦ ɡɚɤɨɧɚɦ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ ɪɚɡɛɢɜɚɟɬɫɹ ɧɚ ɞɜɚ ɷɬɚɩɚ: ɧɚɯɨɠɞɟɧɢɟ ɢɫɤɨɦɵɯ ɫɤɨɪɨɫɬɟɣ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ ɩɪɢ 0 d t d t0 ɢ ɩɪɢ t ! t0 . ɇɟɨɛɯɨɞɢɦɨ ɬɚɤɠɟ ɨɩɪɟɞɟɥɢɬɶ ɦɨɦɟɧɬ ɜɪɟ-
ɦɟɧɢ t0 , ɜ ɤɨɬɨɪɵɣ ɧɚɱɧɟɬɫɹ ɫɤɨɥɶɠɟɧɢɟ ɛɪɭɫɤɚ ɩɨ ɞɨɫɤɟ.
ȼɵɛɟɪɟɦ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.7, ɢ ɢɡɨɛɪɚɡɢɦ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɚ ɫɢɫɬɟɦɵ.
Y
|
R |
|
|
N |
|
Fɬɪ |
F |
Fɬɪ |
|
|
|
mg |
Mg |
X |
|
N |
|
|
Ɋɢɫ. 2.7 |
|
II. Ɂɚɩɢɲɟɦ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɨɫɢ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ, ɨɞɢɧɚɤɨɜɵɟ ɧɚ ɩɟɪɜɨɦ ɢ ɜɬɨɪɨɦ ɷɬɚɩɚɯ ɞɜɢɠɟɧɢɹ, ɭɪɚɜɧɟɧɢɟ ɤɢɧɟɦɚɬɢɱɟɫɤɨɣ ɫɜɹɡɢ (ɩɪɢ t d t0 ) ɢ ɡɚɤɨɧ

60 |
ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ |
Ⱥɦɨɧɬɨɧɚ – Ʉɭɥɨɧɚ (ɩɪɢ t ! t0 ). ȼɜɟɞɟɦ ɨɛɨɡɧɚɱɟɧɢɹ: a ɢ A – ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɣ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ ɧɚ ɨɫɶ X.
Ȼɪɭɫɨɤ ɧɟ ɫɤɨɥɶɡɢɬ ɩɨ ɞɨɫɤɟ |
Ȼɪɭɫɨɤ ɫɤɨɥɶɡɢɬ ɩɨ ɞɨɫɤɟ |
|||
|
ma |
F |
Fɬɪ , |
(2.42) |
|
0 |
N mg , |
(2.43) |
|
|
MA |
Fɬɪ , |
(2.44) |
|
|
0 R N Mg . |
(2.45) |
||
ɂɫɩɨɥɶɡɭɟɦ ɡɚɞɚɧɧɵɣ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ ɡɚɤɨɧ ɢɡɦɟɧɟɧɢɹ |
||||
ɦɨɞɭɥɹ ɫɢɥɵ F ɫɨ ɜɪɟɦɟɧɟɦ: |
F |
Dt . |
(2.46) |
|
|
|
|||
Ⱦɨ ɬɟɯ ɩɨɪ, ɩɨɤɚ ɫɢɥɚ |
ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɧɟɬ ɤɢɧɟ- |
|||
ɬɪɟɧɢɹ ɩɨɤɨɹ ɧɟ ɞɨɫɬɢɝɥɚ ɫɜɨ- |
ɦɚɬɢɱɟɫɤɨɣ ɫɜɹɡɢ ɦɟɠɞɭ ɭɫɤɨ- |
|||
ɟɝɨ ɦɚɤɫɢɦɚɥɶɧɨɝɨ |
ɡɧɚɱɟɧɢɹ, |
ɪɟɧɢɹɦɢ ɛɪɭɫɤɚ ɢ ɞɨɫɤɢ. |
|
|
ɪɚɜɧɨɝɨ ɫɢɥɟ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟ- |
ɉɨɫɤɨɥɶɤɭ ɛɪɭɫɨɤ ɫɤɨɥɶ- |
|||
ɧɢɹ, ɛɪɭɫɨɤ ɢ ɞɨɫɤɚ ɞɜɢɝɚɸɬɫɹ |
ɡɢɬ ɩɨ ɞɨɫɤɟ ɞɥɹ ɫɢɥɵ ɬɪɟɧɢɹ |
|||
ɫ ɨɞɢɧɚɤɨɜɵɦ ɭɫɤɨɪɟɧɢɟɦ: |
|
ɫɤɨɥɶɠɟɧɢɹ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ: |
||
a A . |
(2.47) |
Fɬɪ PN . |
(2.48) |
|
III. Ɋɟɲɢɦ ɩɨɥɭɱɟɧɧɵɟ ɫɢɫɬɟɦɵ ɭɪɚɜɧɟɧɢɣ ɞɥɹ ɤɚɠɞɨɝɨ ɢɡ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɯ ɷɬɚɩɨɜ ɞɜɢɠɟɧɢɹ ɬɟɥ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɫɢɫɬɟɦɵ. ɍɪɚɜɧɟɧɢɟ (2.45) ɧɟ ɢɫɩɨɥɶɡɭɟɬɫɹ ɩɪɢ ɪɟɲɟɧɢɢ ɩɨɫɬɚɜɥɟɧɧɨɣ ɡɚɞɚɱɢ, ɩɨɫɤɨɥɶɤɭ ɧɟ ɬɪɟɛɭɟɬɫɹ ɧɚɯɨɠɞɟɧɢɹ ɫɢɥɵ ɪɟɚɤɰɢɢ ɨɩɨɪɵ R, ɞɟɣɫɬɜɭɸɳɟɣ ɧɚ ɞɨɫɤɭ.
a A |
|
Dt |
, |
(2.49) |
a |
Dt Pmg |
, |
(2.51) |
||
|
M m |
m |
||||||||
|
|
|
|
|
|
|
||||
F |
MDt |
. |
|
(2.50) |
A |
Pmg |
, |
|
(2.52) |
|
|
|
|
|
|||||||
ɬɪ |
M m |
|
|
|
M |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Fɬɪ Pmg . |
|
(2.53) |
||
ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɡɚɤɨɧɨɦ Ⱥɦɨɧɬɨɧɚ – Ʉɭɥɨɧɚ ɦɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɫɢɥɵ ɬɪɟɧɢɹ ɩɨɤɨɹ ɪɚɜɧɨ ɫɢɥɟ ɬɪɟɧɢɹ ɫɤɨɥɶɠɟɧɢɹ (ɫɦ.
(2.13)): |
|
|
MDt0 |
Pmg . |
(2.54) |
M m |
